約数の個数と和　　　　　　　　　　　　　　　　　　

　自然数 Ｎ が、

　　　　 Ｎ＝ｐ^aｑ^b・・・ｒ^c 　　（ｐ＜ｑ＜・・・＜ｒ　は素数、a、b、・・・、c　は ０ 以上の整数）

と素因数分解されるとき、Ｎ の約数の個数 Ｄ と約数の総和 Ｓ は、次の公式で与えられる。

　　　　　　　　　Ｄ＝（ａ＋１)(ｂ＋１)・・・（ｃ＋１）

　　　　　　　　　

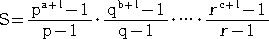
　これらの公式は、順列・組合せや数列の学習のときに、我々の前に登場するものである。

公式の簡明さから、Ｄ → Ｓ の順で発見されたと、今まで思っていたが、事実は逆であった。

公式 Ｄ が発見されたのは、１７６１年　カスチリオーニ によってであり、公式 Ｓ は、それより

古く、１６５８年　イギリスのジョン・ウォーリスによって発見された。

（参考文献：イー・ヤーデップマン　著　藤川　誠　訳　算数の文化史（現代工学社））

例　１２の約数の総和を求めよ。

　１２の約数は、１、２、３、４、６、１２　の６個あり、その総和は、

　　　　１＋２＋３＋４＋６＋１２＝２８

である。一般には、　１２＝２²・３　と素因数分解し、その約数の総和は

　　１＋２＋３＋４＋６＋１２
　＝１＋２＋３＋２²＋２・３＋２²・３
　＝１＋２＋２²＋（１＋２＋２²）・３
　＝(１＋２＋２²)(１＋３)

として求められる。これが、上記で示された公式である。


　上記の話題を一般化して、約数関数（Divisor function） σ_m と言われるものがある。

次のように定義される。

　　　正の整数 ｎ に対して、

　　　　　

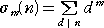
　ここで、ｍ＝０　のとき、

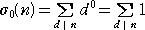＝（ｄ が ｎ の約数のとき、１を加算）＝（ｎ の約数の個数）

　　　　　ｍ＝１　のとき、

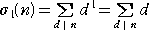＝（ｎ の約数の総和）

である。

例　σ₁（１）＝１　、σ₁（２）＝３　、σ₁（３）＝４　、σ₁（４）＝７　、σ₁（５）＝６　、σ₁（６）＝１２

　ここで、σ₁（ｎ）＝２ｎ　となる数は、完全数と言われる。

例　２８は、完全数である。

　実際に、２８の約数は、１、２、４、７、１４、２８　なので、

　　σ₁（２８）＝１＋２＋４＋７＋１４＋２８＝２×２８　より、２８は完全数である。

　一般に、

　ｎ＝ｐ^ａｑ^ｂ・・・ｒ^ｃ　に対して、

　 σ_ｍ（ｎ）＝（１＋ｐ^ｍ＋・・・＋ｐ^ｍａ）（１＋ｑ^ｍ＋・・・＋ｑ^ｍｂ）・・・（１＋ｒ^ｍ＋・・・＋ｒ^ｍｃ）

である。

例　ｎ＝９００　に対して、　ｎ＝２²・３²・５²

　約数の個数は、　（２＋１）（２＋１）（２＋１）＝２７

　　上記の公式を用いると、

　σ₀（９００）＝（１＋（１が２個））（１＋（１が２個））（１＋（１が２個））

　　　　　　　 ＝（１＋２）（１＋２）（１＋２）＝２７

　約数の総和は、　（１＋２＋２²）（１＋３＋３²）（１＋５＋５²）＝２８２１

　　上記の公式を用いると、

　σ₁（９００）＝（１＋２＋２²）（１＋３＋３²）（１＋５＋５²）＝２８２１


　ここで、面白い性質がある。

　２２０の約数は、　１、２、４、５、１０、１１、２０、２２、４４、５５、１１０、２２０　なので、

　σ₁（２２０）＝１＋２＋４＋５＋１０＋１１＋２０＋２２＋４４＋５５＋１１０＋２２０＝５０４

　５０４から自分自身（２２０）を差し引いた数は、　５０４−２２０＝２８４

　ここで、２８４の約数は、　１、２、４、７１、１４２、２８４　なので、

　σ₁（２８４）＝１＋２＋４＋７１＋１４２＋２８４＝５０４

　５０４から自分自身（２８４）を差し引いた数は、　５０４−２８４＝２２０

　このような　２２０　と　２８４　の関係にある数は、友愛数と言われる。

例　友愛数の例としては、

　　　１１８４　と　１２１０　、　２６２０　と　２９２４　、　・・・

などが知られている。


　当ＨＰの掲示板「出会いの泉」に、ＨＮ「ｈａｓｕ」さんという方が、次のような問題を書き込ま
れた。（平成２３年８月３０日付け）

　この前、本で読んだ問題なのですが、σ（ｘ）＋σ（ｙ）＝σ（ｘ＋ｙ）　となるｘ、ｙ を求める問
題です。ｘ＝１、ｙ＝２ 以外に解はあるのでしょうか？　ここで、σ（ｘ）は約数関数です。


　ＨＮ「ｈａｓｕ」さんが言われる「σ（ｘ）は約数関数」であるが、

　　σ₁（１）＝１、σ₁（２）＝３、σ₁（３）＝４　より、

　　　　　　　　　　　　σ₁（１）＋σ₁（２）＝４＝σ₁（３）＝σ₁（１＋２）

であることと、前後の文脈から、　σ＝σ₁　なのだろう。

　ｘ、ｙ が互いに素のとき、　σ₁（ｘ）・σ₁（ｙ）＝σ₁（ｘ・ｙ）　は成り立つと思われるが、一般の

ｘ、ｙ については成り立ちそうにない。ましてや、σ₁（ｘ）＋σ₁（ｙ）＝σ₁（ｘ＋ｙ）　が成り立つ

ことは、ほとんど期待できないと思われる。


　この私の予想に反して、当ＨＰがいつもお世話になっているＨＮ「らすかる」さんが、解を見
出された。（平成２３年８月３０日付け）

　ｘ≦ｙ　として、(ｘ，ｙ) = (1，2)　の他に

(4，5)、(2，6)、(2，8)、(5，10)、(7，14)、(2，18)、(14，18)、(11，22)、(6，24)、・・・

と無数にあるのではないでしょうか。


　ｈａｓｕさんからのコメントです。（平成２３年８月３０日付け）

　確かに、（ｘ，ｙ，ｘ＋ｙ）と互いに素な数をかければいいので、無限にありますね。でも、原
始ピタゴラス的な組は無限にあるのでしょうか？


　らすかるさんからのコメントです。（平成２３年８月３０日付け）

　証明はわかりませんが、ｙ が素数であるものに限定しても、

　(ｘ，ｙ) = (1，2)、(4，5)、(26，29)、(20，37)、(8，41)、(12，43)、(38，47)、(56，61)、(44，67)、

　　　　　　(62，83)、(40，101)、(76，107)、(56，127)、(92，127)、(24，131)、(112，167)、

　　　　　　(124，167)、(122，173)、(24，179)、(88，179)、(62，191)、(68，197)、(160，197)、

　　　　　　(110，199)、(80，229)、(56，239)、(54，251)、(136，257)、(92，263)、(220，263)、

　　　　　　(182，271)、(212，277)、(170，283)、・・・

のようになりますので、無数にありそうです。


（追記）　平成２６年１１月２６日付け

　約数の和を求めるアイデアが次の問題でも活かされる。

　学習院大学法学部（１９８２）　入試問題

　自然数ｎの十進法表示に表れる数字の積をＦ（ｎ）で表す。例えば、

　　Ｆ（３）＝３　、Ｆ（１５）＝１×５＝５　、Ｆ（３０５）＝０

である。このとき、Σ_ｎ=1〜1000 Ｆ（ｎ） を求めよ。

（解）　題意より、

Σ_ｎ=1〜1000 Ｆ（ｎ）

＝Σ_ｎ=1〜9 Ｆ（ｎ）＋Σ_ｎ=10〜99 Ｆ（ｎ）＋Σ_{ｎ=100〜999} Ｆ（ｎ）＋Ｆ（１０００）

＝（１＋２＋３＋４＋５＋６＋７＋８＋９）

　＋（１＋２＋３＋４＋５＋６＋７＋８＋９）（０＋１＋２＋３＋４＋５＋６＋７＋８＋９）

　＋（１＋２＋３＋４＋５＋６＋７＋８＋９）（０＋１＋２＋３＋４＋５＋６＋７＋８＋９）（０＋１＋２＋３＋４＋５＋６＋７＋８＋９）

　＋０

＝４５＋４５×４５＋４５×４５×４５＋０＝９３１９５　　（終）


（コメント）　括弧を展開すると、それぞれの数における値が求められていることに計算の美
　　　　　　しさを感じる。



　　　以下、工事中