
数を扱うとき、その数の特徴を瞬時に理解することは大切なことである。
例 12345 は、15 の倍数である。
924 は、4 で割り切れる。
123123 は、7 で割り切れる。
分数計算等で、たとえば、1521/612 などを瞬時に 169/68 と約分してみせると、
たいていの生徒はびっくりするが、そのからくりは、数の特徴を知っているかどうかにかか
っている。(分子、分母ともに 9 の倍数なので、9 で割っているにすぎない。)
倍数の判定 
数を扱うとき、その数の特徴を瞬時に理解することは大切なことである。
例 12345 は、15 の倍数である。
924 は、4 で割り切れる。
123123 は、7 で割り切れる。
分数計算等で、たとえば、1521/612 などを瞬時に 169/68 と約分してみせると、
たいていの生徒はびっくりするが、そのからくりは、数の特徴を知っているかどうかにかか
っている。(分子、分母ともに 9 の倍数なので、9 で割っているにすぎない。)
| 倍数 | 判 定 方 法 | |
| 2 | ・・・ | 一の位が2の倍数 |
| 3 | ・・・ | 各位の数の和が3の倍数 |
| 4 | ・・・ | ・下二桁が4の倍数 |
| ・一の位を2で割った数を十の位に足した数が偶数 | ||
| 5 | ・・・ | 一の位が5の倍数 |
| 6 | ・・・ | 2かつ3の倍数 |
| 7 | ・・・ | ・3桁毎に交互に足したり引いたりしてできた数が7の倍数 |
| ・3桁の数 abc で、ab-2c が7の倍数(→詳細は、こちら) 一般に、10p+q において、p-2q が7の倍数(→詳細はこちら) |
||
| ・3桁の数 abc で、2a+bc が7の倍数(→詳細は、こちら) 一般に、100p+q において、2p+q が7の倍数(→詳細はこちら) |
||
| ・6桁の場合、2桁毎に7で割った余りを考え、それらの数で出来る2桁の | ||
| 整数の差が7の倍数(→詳細は、こちら) | ||
| 8 | ・・・ | ・下3桁が8の倍数 |
| ・一の位を2で割り十の位に足して2で割った数を百の位に足した数が偶数 | ||
| 9 | ・・・ | 各位の数の和が9の倍数 |
| 10 | ・・・ | 一の位が0 |
| 11 | ・・・ | 各位の数を交互に足したり引いたりしてできた数が11の倍数 |
| 12 | ・・・ | 3かつ4の倍数 |
| 13 | ・・・ | 7の倍数の判定と同じ |
| ・x=a+10p → 4a+pが13の倍数(→詳細は、こちら) | ||
| ・x=p+100q → p+9qが13の倍数(→詳細は、こちら) | ||
| 14 | ・・・ | 2かつ7の倍数 |
| 15 | ・・・ | 3かつ5の倍数 |
| 16 | ・・・ | 下4桁を2で割った数が8の倍数(下4桁を4で割った数が4の倍数) |
| 17 | ・・・ | ・十位以上の数から一位の数の5倍を引いた数が17の倍数 |
| ・2桁毎に下位から2のべきを掛けて交互に足したり引いたりしてできた数 | ||
| が17の倍数 | ||
| ・x=p+100q → p-2q が17の倍数(→詳細は、こちら) | ||
| ・x=a+10b+100q → a-7b-2q が17の倍数(→詳細は、こちら) | ||
| 18 | ・・・ | 2かつ9の倍数 |
| 19 | ・・・ | 各位の数に上位から2のべきを掛けて足した数が19の倍数 |
| ・x=p+100q → p+5q が19の倍数(→詳細は、こちら) | ||
| 20 | ・・・ | 4かつ5の倍数 |
| 21 | ・・・ | 3かつ7の倍数 |
| 22 | ・・・ | 2かつ11の倍数 |
| 23 | ・・・ | 十位以上の数と一位の数の7倍の和が23の倍数 |
| ・x=p+100q → p+8q が23の倍数(→詳細は、こちら) | ||
| 24 | ・・・ | 3かつ8の倍数 |
| 27 | ・・・ | x=p+1000q → p+q が27の倍数 |
| 29 | ・・・ | ・x=p+10000q → p-5q ・x=p+30q → p+q |
| 37 | ・・・ | 3桁毎に区分けした数を足した数が37の倍数 |
| 999 | ・・・ | 3桁毎に区分けした数を足した数が999の倍数 |
上記の判定方法を統一的に理解するために、次のことを知らなくてはならない。
十進法展開 : N = a×10n+・・・+b×102+c×10+d
( ただし、a、・・・、b、c、d は整数で、0 ≦ a、・・・、b、c、d ≦ 9、a≠0 )
合同式については、こちら を参照
さて、倍数の判定について、その理論的根拠をまとめておこう。
2 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10とそのべきは、2の倍数なの
で、一の位の数 d が2の倍数かどうかを判断すればよい。
3 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10≡1 (mod 3)から、
10n≡1 (mod 3)である。
よって、N ≡ a+・・・+b+c+d となり、N ≡ 0 (mod 3)となるためには、
a+・・・+b+c+d ≡ 0 (mod 3)であることが必要十分である。
4 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、102≡0 (mod 4)であるの
で、c×10+d すなわち、下二桁が4の倍数かどうかが、Nが4の倍数かどうかを判断する
基準となる。
広島工業大学の大川研究室から、次のような判定法があることをお教えいただいた。
c×10+d が4の倍数のとき、c×10+d=4k (k は整数)とおける。このとき、
c×10+d ≡ d ≡ 0 (mod 2)なので、d=2d’とおける。よって、c×10+2d’=4k
より、5c+d’=2k なので、5c+d’≡c+d’≡0 (mod 2)となる。
逆に、c+d’≡0 (mod 2)のとき、c×10+d は4の倍数となる。
5 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10とそのべきは、5の倍数なの
で、一の位の数 d が5の倍数かどうかを判断すればよい。
6 の倍数の判定 :
6=2×3 で、2と3は互いに素であることから、2の倍数かつ3の倍数かどうかを調べれ
ばよい。
7 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、103≡-1 (mod 7)であるの
で、末位から3桁ごとに区切った数A0(=b×102+c×10+d)、A1、・・・、Am について、
N = Am×103m+・・・+A1×103+A0≡A0-A1+A2-・・・ (mod 7)
よって、N が7の倍数となるためには、A0-A1+A2-・・・≡ 0 (mod 7)であることが必
要十分である。
(コメント) この7の倍数の判定法については少し不満がある。簡単な計算で求められない
ので、多分実際に割った方が早いだろう!もっと簡便な方法がないかどうか、今後の
研究課題としたい。
例 7桁の数 2198455 は7の倍数か?
2-198+455=259=7×37 なので、7の倍数である。
上記の判定法では、必ず最後に3桁の数が7の倍数かどうかの判定が要求される。3桁の
数については、次のような判定法が知られている。
3桁の数 abc が、7の倍数になるのは、ab-2c が7の倍数のとき
言葉では説明が長くなってしまうので、次の例で理解してもらいたい。
例 259 について、25-9×2=7 が7の倍数なので、259も7の倍数。
(理論的根拠) 3桁の数 a×102+b×10+c =10(a×10+b)+c と変形することに
より、3桁の数は、10A+c (Aは上位2桁の数)と書ける。このとき、
10A+c≡0 (mod 7)ならば、
10A+c≡20A+2c≡-A+2c≡A-2c≡0 (mod 7)
逆に、A-2c≡0 (mod 7)のとき、
2(10A+c)=20A+2c≡20A+2c+A-2c (mod 7)なので、
2(10A+c)≡21A≡0 (mod 7)
2と7は互いに素なので、10A+c≡0 (mod 7)である。(→ 参考:「7の倍数」)
(追記) 平成21年4月21日付け
上記の3桁の場合の7の倍数の判定方法が、朝日新聞(4/21付け朝刊)の科学のページ
のコラム「小島寛之の数学カフェ」で取り上げられた。
その中で、「けたが増えれば、これを繰り返せばいい。」とあるが、どのような計算をすれば
いいのか、よく分からなかった。
上記の計算は、3桁の場合に限定した特別な計算なので、桁が増えた場合は、たとえば、
2198455 は、「2-198+455=259=7×37」 のように全体を見据えて計算しない
と正しい倍数の判定は出来ないと思う。
小島先生は、どのような計算を考えて上記の文章に至ったのか、全く不明である。今度、
朝日新聞に問い合わせてみよ~っと!
上記の私の疑問に対して、当HPがいつもお世話になっているHN「攻略法」さんが答えて
くれた。
3桁の数 abc が、7の倍数になるのは、ab-2c が7の倍数のとき
を一般化したもののようだ。(平成23年7月4日付け)
十の位以上と一の位を切り離し、前者から後者の2倍を引く。この操作を繰り返して、2桁か
1桁になって、それが7の倍数なら元の数も7の倍数となる。
例 2198455の場合
219845-2*5=219835
21983-2*5=21973
2197-2*3=2191
219-2*1=217
21-2*7=7
例 864197523861の場合
86419752386-2*1=86419752384
8641975238-2*4=8641975230
864197523-2*0=864197523
86419752-2*3=86419746
8641974-2*6=8641962
864196-2*2=864192
86419-2*2=86415
8641-2*5=8631
863-2*1=861
86-2*1=84
8-2*4=0
実際に、このことを証明してみよう。
k桁の自然数AB…CDが7の倍数になるのは、AB…C-2*D が7の倍数のとき
(証明) 2*AB…CD+(AB…C-2*D)=2*(10*AB…C+D)+AB…C-2*D=21*AB…C より、
AB…C-2*D が7の倍数のとき、AB…CD は7の倍数になる。 (証終)
上記は、整数を10単位で切った場合だが、100単位で切った場合も同様の性質が成り
立つ。
3桁の数 abc が、7の倍数になるのは、2a+bc が7の倍数のとき
(証明) abc=100a+bc≡2a+bc (mod 7) (証終)
一般に、「百の位以上と十、一の位を切り離す」とき、
k桁の自然数AB…CDが7の倍数になるのは、2*A…B+CD が7の倍数のとき
(証明) A…BCD=A…B*100+CD=A…B*(7*14+2)+CD≡2*A…B+CD (mod 7) (証終)
例 2198455の場合
2*21984+55=44023
2*440+23=903
2*9+3=21
例 864197523861の場合
2*8641975238+61=17283950537
2*172839505+37=345679047
2*3456790+47=6913627
2*69136+27=138299
2*1382+99=2863
2*28+63=119
2*1+19=21
(コメント) 小島先生の「繰り返し」の意味が分かりました!攻略法さんに感謝します。
(追記) 平成21年11月21日付け
当HPの読者であるHN「jaiaso」さんから、7の倍数の判定法で上記で述べた方法とは異
なるものがある旨、ご教示いただいた。その方法は、
中村義作 著 コンピュータもびっくり!速算100のテクニック(講談社ブルーバックス)
に書かれているとのこと。早速その書籍を買い求め、研究を行った。
上記では、 103≡-1 (mod 7) であることを用いて、3桁毎に交互に足したり引いた
りしてできる数が7の倍数かどうかで判定した。
新しい方法では、 106≡1 (mod 7) であることに注目する。
このとき、 ab・・・c000000 ≡ ab・・・c (mod 7) となるので、基本的には6桁以下の
数について議論すればよいことが分かる。
そこで、(見かけ上)6桁の数を、
abcdef=a×105+b×104+c×103+d×102+e×10+f
とおき、末尾から2桁ずつ組み合わせて、
abcdef=(a×105+b×104)+(c×103+d×102)+e×10+f
と考える。ここで、
a×10+b ≡ A (mod 7)、c×10+d ≡ B (mod 7)、e×10+f ≡ C (mod 7)
とおくと、 abcdef≡A×104+B×102+C (mod 7) となる。
ところで、 104=10・103≡-10≡4 (mod 7) 、102≡2 (mod 7) であるので、
abcdef≡4A+2B+C (mod 7) となる。
したがって、(10B+C)-(10A+B)=-10A+9B+C≡4A+2B+C (mod 7)
であることから、6桁の数 abcdef が7で割り切れるためには、
(10B+C)-(10A+B) が7の倍数
であることが必要十分である。
例 6桁の数 227752 は7の倍数か?
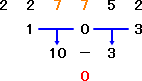 |
左図の計算から、 227752 は7の倍数である。 |
(コメント) 3桁ずつ区切るよりも、この方が計算が簡単ですね!この解法をご教示いただい
た jaiaso さんに感謝します。
この解法を用いると、先に上げた例も次のように解かれる。
例 7桁の数 2198455 は7の倍数か?
2000000 ≡ 2 (mod 7) なので、
2198455 ≡ 198455+2=198457 (mod 7)
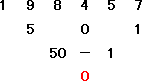 |
左図の計算から、 198457 は7の倍数である。 |
したがって、 2198455 は7の倍数である。
上記の計算では、「2」を6桁の数に加えたが、6桁の場合と同様の計算を7桁目以降につ
いても適用すれば次のような計算となる。
例 12桁の数 864197523861 は7の倍数か?
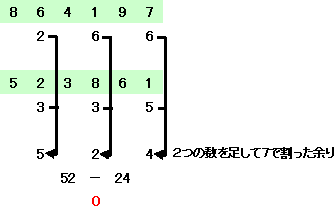 |
左図の計算から、12桁の数 864197523861 は7の倍数である。 |
(追記) 当HP読者のHN「ダイナマイト高柳」さんが、7の倍数の判定方法について考察さ
れました。(平成24年11月16日付け)
少し設定を変えて計算していたら、合同式なしで理解できる方法にたどりつきました。直観
的にも理解しやすいのではないかと期待しております。
7の倍数の判定法について、「10以上の位と、1の位を切り離し、前者から後者の2倍を引
く。この操作を繰り返し、2桁か1桁になったとき、それが7の倍数なら元の数も7の倍数であ
る」というものがありましたね。
ある整数をxとおき、その1桁目をyとおくと、前述の操作は、
(x-y)/10-2y=(x-21y)/10
で表されます。
xもyも整数で、x-21yは常に10の倍数
(∵xと21yの一の位は同一ですから、(x-21y)/10も常に整数です。)
また、21は7の倍数ですから、xが7の倍数のとき、x-21yは常に10の倍数かつ7の倍数
xが7の倍数でないとき、x-21yは常に10の倍数であるが、7の倍数でない
(∵ある整数nの倍数同士の和差は常にnの倍数、また、ある整数nの倍数と、nの倍数でない
数の和差は常にnの倍数でない)
つまり、この操作を行ったとき、
・操作後の整数が7の倍数であれば、常にxは7の倍数
・操作後の整数が7の倍数でなければ、常にxは7の倍数ではない
ということになります。ところで、この考え方はそのまま次のように拡張されます。
ある数をx、その1桁目をyとおいて、yにかける数をaとおくと、上記の操作は
(x-y)/10-ay={x-(10a+1)y}/10
ですから、xがある整数bの倍数であるとき、10a+1がbの倍数であるようなaを定めると、
{x-(10a+1)y}/10もまたbの倍数ということになります。
つまり、これは、bの倍数でないかと考えた整数をみつけたら、bの倍数であるような下一桁
が1である数を見つけ、その10以上の桁部分をaとして、7の倍数判定のときと同じようにひい
てやれば発見できるということです。
ところで、aは正でも負でも構わないわけですから、10a+1を鑑みますと、下一桁が9であ
るようなbの倍数でも良さそうですね。
(追記) 当HP読者の方より、7の倍数の判定法についてメールを頂いた。
(平成24年11月25日付け)
7の倍数判定法について既出以外の方法がありますので、証明方法と併せて紹介させて
頂ければと思いメールさせて頂きました。
ある自然数Nについて、N=Σk=0~n ak・10k と置くことができる。
ここで、mod 7 として、 1 ≡ 1 、10 ≡ 3 、102 ≡ 9 ≡ 2 、103 ≡ 27 ≡-1 、
104 ≡ 4 ≡-3 、105 ≡ -2 、106 ≡ (-1)2 ≡ 1 、・・・・・
から、「1,3,2,-1,-3,-2」が循環的に続くことが推察される。このとき、mod 7 として、
N≡(a0-a3+a6-・・・)+3(a1-a4+a7-・・・)+2(a2-a5+a8-・・・)
が成り立つことがわかる。よって、Nが7の倍数であるかどうかは、各桁の数字を抽出して、
(a0-a3+a6-・・・)+3(a1-a4+a7-・・・)+2(a2-a5+a8-・・・)
を計算し、これが7の倍数であることを言えばよい。
また、7・10kが7の倍数であることに注意すると、各桁で7以上の数については、これから7
を引いても自然数Nの剰余の性質は保存されるから、係数は、mod 7で考えれば十分である。
例 41371295 は7の倍数かどうかを判定せよ。
41301225について考えればよいので、(5-1+1)+3(2-0+4)+2(2-3)=5+18-2=21
これは、7で割り切れるので、41371295 は7の倍数である。
(※) 偶然ではあるのでしょうが、10のべき乗数の余りが、1,3,2,-1,-3,-2・・・と循環すること
に気付いたときには鳥肌が立ちました。恐縮ながら、参考になれば幸いです。
(コメント) 新しい視点からの考察、感動しました。別解に感謝します。さらに、追認してみま
した。
例 12桁の数 864197523861 は7の倍数か?
164120523161と変換し、
(1-3+0-4)+3(6-2+2-6)+2(1-5+1-1)=-6-8=-14
これは、7の倍数なので、864197523861 は7の倍数である。
(計算そのものが単純で、分かりやすいですね!)
(追記) 令和2年8月28日付け
111111は7の倍数か?という問題に対して、7×11×13=1001 であることを知って
いれば、
111111=111×1001=111×7×11×13 と素因数分解できるので、7の倍数
と答える方も多いでしょう。
もちろん、7の倍数の判定方法から、
3桁毎に区切って、 111-111=0 から、7の倍数
2桁毎に区切って7で割った余りから、2桁の整数の差 44ー44=0 から、7の倍数
としてもよい。
8 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、103≡0 (mod 8)であるので、
b×102+c×10+d すなわち、下三桁が8の倍数かどうかが、Nが8の倍数かどうかを判
断する基準となる。
広島工業大学の大川研究室から、次のような判定法があることをお教えいただいた。
b×102+c×10+d が8の倍数のとき、b×102+c×10+d=8k (k は整数)とおけ
る。このとき、b×102+c×10+d ≡ d ≡ 0 (mod 2)なので、d=2d’とおける。
よって、b×102+c×10+2d’=8k より、b×50+5c+d’=4k なので、
b×50+5c+d’≡c+d’≡0 (mod 2)となる。
c+d’=2d”とおけるので、b×50+5c+d’=4k に代入して、b×50+4c+2d”=4k
となる。
よって、b×25+2c+d”=2k より、b+d”≡0 (mod 2)
逆に、b+d”≡0 (mod 2)のとき、b×102+c×10+d は8の倍数となる。
9 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10≡1 (mod 9)から、
10n≡1 (mod 9)である。
よって、N ≡ a+・・・+b+c+d となり、N ≡ 0 (mod 9)となるためには、
a+・・・+b+c+d ≡ 0 (mod 9)であることが必要十分である。
(追記) 令和2年10月8日付け
9の倍数の性質を利用したゲームです。
問題 1~9の9個の数字を1回ずつ全部使って2数A、Bを作り、A+B=Cとする。A、Bを
隠し、Cのある位の数を隠す。その数を当てよ。
(解) C≡1+2+3+・・・+9=45≡0 (mod 9) なので、
例えば、mod 9 で、C≡2 のとき、隠した数は、7であることが分かる。 (終)
10 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10とそのべきは、10の倍数な
ので、一の位の数 d が0かどうかを判断すればよい。
11 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、10≡-1 (mod 11)であるの
で、 N ≡ a×(-1)n+・・・+b×(-1)2+c×(-1)+d (mod 11)
よって、N が11の倍数となるためには、d-c+b-・・・≡ 0 (mod 11) であることが必
要十分である。
例 6桁の数 674135 は11の倍数か?
6-7+4-1+3-5=0 なので、11の倍数である。
攻略法さんから、次のような判定法があることをご教示いただいた。(平成23年7月6日付け)
十の位以上をX、一の位をYとすると、元の数は、10X+Y である。このとき、
10X+Y が11の倍数であるための必要十分条件は、X-Y が11の倍数であること
(証明) 10X+Y≡0 (mod 11) とすると、Y≡-10X (mod 11) より、
-Y≡10X (mod 11) なので、 X-Y≡11X≡0 (mod 11)
逆に、 X-Y≡0 (mod 11) とすると、 X≡Y (mod 11) なので、
10X≡10Y (mod 11) より、 10X+Y≡11Y≡0 (mod 11) (証終)
例 674135の場合
67413-5=67408
6740-8=6732
673-2=671
67-1=66 ・・・ 11の倍数
さらに、攻略法さんから、次のような判定法があることをご教示いただいた。
(平成23年7月6日付け)
百の位以上をX、一十の位をYとすると、元の数は、100X+Y である。このとき、
100X+Y が11の倍数であるための必要十分条件は、X+Y が11の倍数であること
(証明) 100X+Y≡0 (mod 11) とすると、Y≡-100X (mod 11) より、
X+Y≡-99X≡0 (mod 11)
逆に、 X+Y≡0 (mod 11) とすると、 X≡-Y (mod 11) なので、
100X≡-100Y (mod 11) より、 100X+Y≡-99Y≡0 (mod 11) (証終)
例 674135 の場合
6741+35=6776 繰り返して、 67+76=143 、1+43=44 よって、11の倍数
12 の倍数の判定 :
12=3×4 で、3と4は互いに素であることから、3の倍数かつ4の倍数かどうかを調べれ
ばよい。
13 の倍数の判定 :
N = a×10n+・・・+b×102+c×10+d において、103≡-1 (mod 13)である
ので、末位から3桁ごとに区切った数
A0(=b×102+c×10+d)、A1、・・・、Am について、
N = Am×103m+・・・+A1×103+A0≡A0-A1+A2-・・・ (mod 13)
よって、N が13の倍数となるためには、A0-A1+A2-・・・≡ 0 (mod 13) であること
が必要十分である。
13の倍数の判定A x=a+10p → 4a+pが13の倍数
(例) 156=13・12 で13の倍数だが、判定法によれば、
6+10・15 → 4・6+15=39 が13の倍数なので、156は13の倍数
(証明) 4x=4a+40p≡4a+p (mod 13)
4a+p≡0 (mod 13) ならば、 4x≡0 (mod 13)
4と13は互いに素なので、 x≡0 (mod 13) (証終)
13の倍数の判定B x=p+100q → p+9qが13の倍数
(例) 156=13・12 で13の倍数だが、判定法によれば、
56+100・1 → 56+9=65 が13の倍数なので、156は13の倍数
(証明) x=p+100q≡p+9q (mod 13)
p+9q≡0 (mod 13) ならば、 x≡0 (mod 13) (証終)
読者のために練習問題を置いておこう。
練習問題1 3523は13の倍数であることを示せ。
実際に、3523÷13を求めれば、答は271と割り切れるので、13の倍数としてもよいが、
暗算で次のようにしてもよいだろう。
(解) 4・3+352=364 → 4・4+36=52 → 4・2+5=13 は13の倍数なので、
3523は13の倍数。 (終)
練習問題2 114751は13の倍数であることを示せ。
(解) 4・1+11475=11479 → 4・9+1147=1183 → 83+9・11=182
→ 82+9・1=91 → 4・1+9=13 は13の倍数なので、
114751は13の倍数。 (終)
14 の倍数の判定 :
14=2×7 で、2と7は互いに素であることから、2の倍数かつ7の倍数かどうかを調べれ
ばよい。
15 の倍数の判定 :
15=3×5 で、3と5は互いに素であることから、3の倍数かつ5の倍数かどうかを調べ
ればよい。
16 の倍数の判定 :
N = a×104+b において、104≡0 (mod 16)なので、Nが16の倍数であることと、
b が16の倍数であることは同値である。
したがって、b を2で割った数が8の倍数であることをみればよい。
(もちろん、b を4で割った数が4の倍数であることをみてもよい。)
17 の倍数の判定 :
N = a×10+b において、a-5b=17n (n は整数)のとき、
N =(5b+17n)×10+b=51b+170n=17×(3b+10n)より、Nは、17の倍数。
または、
末位から2桁ごとに区切った数 A0、A1、・・・、Am について、
N = Am×102m+・・・+A1×102+A0 と書ける。102n≡(-2)n (mod 17)なの
で、N ≡A0-2A1+4A2-・・・ (mod 17)
よって、N が17の倍数となるためには、A0-2A1+4A2-・・・≡ 0 (mod 17) であるこ
とが必要十分である。
例 6桁の数 674135 は17の倍数か?
35-2×41+4×67=221=17×13 なので、17の倍数である。
17の倍数の判定A x=p+100q → p-2q が17の倍数
(例) 323=17・19 で17の倍数だが、判定法によれば、
23-2・3=17 より、323は17の倍数
(証明) x=p+100q≡p-2q (mod 17)
p-2q≡0 (mod 17) ならば、 x≡0 (mod 17) (証終)
17の倍数の判定B x=a+10b+100q → a-7b-2q が17の倍数
(例) 323=17・19 で17の倍数だが、判定法によれば、
3-7・2-2・3=-17 より、323は17の倍数
(証明) x=a+10b+100q≡a-7b-2q (mod 17)
a-7b-2q≡0 (mod 17) ならば、 x≡0 (mod 17) (証終)
読者のために練習問題を置いておこう。
練習問題 10999は17の倍数であることを示せ。
(解) 99-2・109=-119 → 19-2・1=17 は17の倍数なので、
10999は13の倍数。 (終)
18 の倍数の判定 :
18=2×9 で、2と9は互いに素であることから、2の倍数かつ9の倍数かどうかを調べれ
ばよい。
19 の倍数の判定 :
N = a×10n+b×10n-1+・・・+c×10+d において、
2nN = a×20n+2b×20n-1+・・・+2n-1c×20+2nd
20≡1 (mod 19)なので、2nN ≡ a+2b+・・・+2n-1c+2nd (mod 19)
このとき、2n は19で割り切れないので、N が19の倍数となるためには、
a+2b+・・・+2n-1c+2nd≡ 0 (mod 19)
であることが必要十分である。
例 3桁の数 323 は19の倍数か?
3+2×2+4×3=19 なので、19の倍数である。
19の倍数の判定A x=p+100q → p+5q が19の倍数
(例) 323=19・17 で19の倍数だが、判定法によれば、
23+5・3=38 は19の倍数なので、323は19の倍数
(コメント) 2のべきを掛けていく判定法に比べて、こちらの方が計算が楽かな?
(証明) x=p+100q≡p+5q (mod 19)
p+5q≡0 (mod 19) ならば、 x≡0 (mod 19) (証終)
20 の倍数の判定 :
20=4×5 で、4と5は互いに素であることから、4の倍数かつ5の倍数かどうかを調べれ
ばよい。
21 の倍数の判定 :
21=3×7 で、3と7は互いに素であることから、3の倍数かつ7の倍数かどうかを調べれ
ばよい。
22 の倍数の判定 :
22=2×11 で、2と11は互いに素であることから、2の倍数かつ11の倍数かどうかを
調べればよい。
23 の倍数の判定 :
N = a×10+b において、a+7b=23n (n は整数)のとき、
N =(-7b+23n)×10+b=-69b+230n=23×(-3b+10n) より、
Nは、23の倍数となる。
(コメント) この判定法は、果たして実戦的なのだろうか?
攻略法さんから、次のような判定法があることをご教示いただいた。(平成23年7月6日付け)
末位から2桁ごとに区切った数
A0、A1、・・・、Am について、元の数
N=Am・102m+・・・+A1・102+A0 が23の倍数であるための必要十分条件は、
Am+・・・+A1・3m-1+3m・A0≡0
(mod 23)
(証明) 3m・N=3m・Am・102m+・・・+3m・A1・102+3m・A0
=300m・Am+・・・+300・A1・3m-1+3m・A0
ここで、 300≡1 (mod 23) なので、
3m・N≡Am+・・・+A1・3m-1+3m・A0
(mod 23)
3m は、23で割り切れないので、
Am+・・・+A1・3m-1+3m・A0≡0 (mod 23) であることが必要十分である。 (証終)
例 1182936の場合
1+18*3+29*32+36*33=1288=23*56
とするか、
繰り返して、 12+88*3=276 、2+76*3=230
23の倍数の判定A x=p+100q → p+8q が23の倍数
(例) 1357=23・59 で23の倍数だが、判定法によれば、
57+8・13=161 → 61+8・1=69 は23の倍数なので、1357は23の倍数
(証明) x=p+100q≡p+8q (mod 23)
p+8q≡0 (mod 23) ならば、 x≡0 (mod 23) (証終)
24 の倍数の判定 :
24=3×8 で、3と8は互いに素であることから、3の倍数かつ8の倍数かどうかを調べれ
ばよい。
27の倍数の判定 x=p+1000q → p+q が27の倍数
(例) 1053=27・39 で27の倍数だが、判定法によれば、
53+1=54 は27の倍数なので、1053は27の倍数
(証明) x=p+1000q≡p+q (mod 27)
p+q≡0 (mod 27) ならば、 x≡0 (mod 27) (証終)
29の倍数の判定 x=p+10000q → p-5q が29の倍数
(例) 10034=29・346 で29の倍数だが、判定法によれば、
34-5=29 は29の倍数なので、10034は29の倍数
(証明) x=p+10000q≡p-5q (mod 29)
p-5q≡0 (mod 29) ならば、 x≡0 (mod 29) (証終)
同様に、 x=p+30q → p+q が29の倍数
(証明) x=p+30q≡p+q (mod 29)
p+q≡0 (mod 29) ならば、 x≡0 (mod 29) (証終)
37 の倍数の判定 :
末位から3桁ごとに区切った数 A0、A1、・・・、Am について、
N = Am×103m+・・・+A1×103+A0 と書ける。103n≡1 (mod 37)なので、
N ≡A0+A1+A2+・・・ (mod 37)
よって、N が37の倍数となるためには、A0+A1+A2+・・・≡ 0 (mod 37) であるこ
とが必要十分である。
例 8桁の数 42674135 は37の倍数か?
42+674+135=851=37×23 なので、37の倍数である。
999 の倍数の判定 :
末位から3桁ごとに区切った数 A0、A1、・・・、Am について、
N = Am×103m+・・・+A1×103+A0 と書ける。103n≡1 (mod 999)なので、
N ≡A0+A1+A2+・・・ (mod 999)
よって、N が999の倍数となるためには、A0+A1+A2+・・・≡ 0 (mod 999) であ
ることが必要十分である。
例 (参考→「虫食い算4」)
攻略法さんが、倍数の判定について、一般化を試みられた。(平成23年8月24日付け)
N =
a×10+b において、
a-5b=17n (n は整数)のとき、Nは、17の倍数
a+7b=23n (n
は整数)のとき、Nは、23の倍数
と判定することができた。
このことの一般化を考えてみた。
A=aB+b とおいて、gcd(d,m)=1 で、da干cb=mn (nは整数)のとき、
dA=d(aB+b)=(±cb+mn)B+db=±(cB±d)b+mnB
において、
cB±d が m の倍数なら、Aは、m の倍数となる。
B=10 なら、Aは、十の位以上の a と一の位の b
とに切り離される。
いくつか例をみていこう。
(1) 3、9の倍数の場合(※既出)
A=x・・・yz=(x・・・y)・10+z
gcd(1,3)=1、gcd(1,9)=1 より、 m=3、9 に対する dの候補として、 d=1
d=1 で、c=1 とすると、 cB-d=1・10-1=9 は、3または9の倍数
よって、 da+cb=1・(x・・・y)+1・z が、3または9の倍数のとき、Aは、3または9の倍
数となる。このことを繰り返して、
x+・・・+y+z が、3または9の倍数のとき、Aは、3または9の倍数となる。
(2) 6、12の倍数の場合、2の倍数かどうか、4の倍数かどうかは下1桁、下2桁を見て
瞬時に判断できるので、後は、3の倍数かどうかを見ればよい。
A=x・・・yz=(x・・・y)・10+z
gcd(2,3)=1 より、 d=2 で、さらに、c=1 とすると、
cB+d=1・10+2=12 が、3の倍数より、
da-cb=2・(x・・・y)-1・z が、3の倍数のとき、Aは、3の倍数となる。
例 1815726 の場合
1815726 は明らかに、2の倍数である。
2・181572-6=363138 繰り返して、 2・36313-8=72618 、2・7261-8=14514
2・1451-4=2898 、2・289-8=570 、2・57-0=114 、2・11-4=18 これは、3の倍数
よって、2かつ3の倍数であることから、6の倍数となる。
(3) 7の倍数の場合(※既出)
A=x・・・yz=(x・・・y)・10+z
gcd(1,7)=1 より、 d=1 で、さらに、c=2 とすると、
cB+d=2・10+1=21 が、7の倍数より、
da-cb=1・(x・・・y)-2z が、7の倍数のとき、Aは、7の倍数となる。
例 17283 の場合
1728-2・3=1722 繰り返して、 172-2・2=168 、16-2・8=0 よって、7の倍数
(4) 11の倍数(※既出)
A=x・・・yz=(x・・・y)・10+z
gcd(1,11)=1 より、 d=1 で、さらに、c=1 とすると、
cB+d=1・10+1 が、11の倍数より、
da-cb=1・(x・・・y)-1・z が、11の倍数のとき、Aは、11の倍数となる。
A=x・・・yzw=(x・・・y)・100+zw
gcd(1,11)=1 より、 d=1 で、さらに、c=1 とすると、
cB-d=1・100-1=99 が、11の倍数より、
da+cb=1・(x・・・y)+1・zw が、11の倍数のとき、Aは、11の倍数となる。
例 674135 の場合
6741+35=6776 繰り返して、 67+76=143 、1+43=44 よって、11の倍数
(5) 13の倍数
A=x・・・yz=(x・・・y)・10+z
gcd(1,13)=1 より、 d=1 で、さらに、c=4 とすると、
cB-d=4・10-1=39 が、13の倍数より、
da+cb=1・(x・・・y)+4z が、13の倍数のとき、Aは、13の倍数となる。
例 3198 の場合
319+4・8=351 繰り返して、 35+4・1=39 よって、13の倍数
(6) 17の倍数
A=x・・・yz=(x・・・y)・10+z
gcd(1,17)=1 より、 d=1 で、さらに、c=5 とすると、
cB+d=5・10+1=51 が、17の倍数より、
da-cb=1・(x・・・y)-5z が、17の倍数のとき、Aは、17の倍数となる。
例 674135 の場合
67413-5・5=67388 繰り返して、 6738-5・8=6698 、669-5・8=629 、62-5・9=17
よって、13の倍数
(7) 19の倍数
A=x・・・yz=(x・・・y)・10+z
gcd(1,19)=1 より、 d=1 で、さらに、c=2 とすると、
cB-d=2・10-1=19 が、19の倍数より、
da+cb=1・(x・・・y)+2z が、19の倍数のとき、Aは、19の倍数となる。
例 4674 の場合
467+2・4=475 繰り返して、 47+2・5=57 、5+2・7=19 よって、19の倍数
(8) 23の倍数
A=x・・・yz=(x・・・y)・10+z
gcd(1,23)=1 より、 d=1 で、さらに、c=7 とすると、
cB-d=7・10-1=69 が、23の倍数より、
da+cb=1・(x・・・y)+7z が、23の倍数のとき、Aは、23の倍数となる。
例 1182936の場合
118293+7・6=118335 繰り返して、 11833+7・5=11868 、1186+7・8=1242
124+7・2=138 、13+7・8=69 よって、23の倍数
(9) 29の倍数
A=x・・・yz=(x・・・y)・10+z
gcd(1,29)=1 より、 d=1 で、さらに、c=3 とすると、
cB-d=3・10-1=29 が、29の倍数より、
da+cb=1・(x・・・y)+3z が、29の倍数のとき、Aは、29の倍数となる。
例 71543 の場合
7154+3・3=7163 繰り返して、 716+3・3=725 、72+3・5=87
8+3・7=29 よって、29の倍数
(コメント) 統一的に倍数を判定できる方法で、感動しました!攻略法さんに感謝します。
(追記) 倍数判定(素数限定)を、GAI さんよりご投稿いただきました。(平成29年7月3日付け)
Nを自然数とするとき、Nが素数pで割れるのかを、次のキーナンバー(K(p))を使うことで手
軽に判定できる。
≪キーナンバー≫
K(3) = 1、K(19)=2、K(29)= 3、K(13)= 4、K(7)=5、K(59)=6、K(23)=7、K(79)=8、K(89)=
9
K(11)=10、・・・、
K(11)=-1、K(7)=-2、K(31)=-3、K(41)=-4、K(17)=-5、K(61)=-6、K(71)=-7、K(?)=-8、
K(13)=-9、K(101)=-10、・・・
<方法>
① Nの最下位を除いた残りでできる数+最下位の数*K(p)を新たにNとする。
② 上記の作業を繰り返す。
③ N=p または N=0 になれば、Nは素数pで割り切れる。
#具体例1・・・N=6179011は、59で割れるか?
K(59)=6 より、N=617901+1*6=617907、N=61790+7*6=61832 、N=6183+2*6=6195
N=619+5*6=649 、N=64+9*6=118 、N=11+8*6=59
→ 元のN=6179011は、59で割り切れる。
#具体例2・・・N=6973481は、31で割れるか?
K(31)=-3 より、N=697348-1*3=697345 、N=69734-5*3=69719 、N=6971-9*3=6944
N=694-4*3=682 、N=68-2*3=62 、N=6-2*3=0
→ 元のN=6973481は、31で割り切れる。
なお、p=2、5以外のp<1000までのキーナンバーK(p)→一覧 のようになる。
らすかるさんからのコメントです。(平成29年7月3日付け)
K(?)=-8 の「?」には、81の約数が入らなければならないので、K(3)しかないですね。
K(983)=295 ですが、大きい数はうまくないですね。
(例) N=1966は、983で割れるか?
K(983)=295 より、N=196+6*295=1966 、N=196+6*295=1966 、N=196+6*295=1966、・・・
DD++さんからのコメントです。(平成29年7月4日付け)
「素数限定」って、これ本当ですかね?直感的には、10と互いに素なら使えそうに思えます
が、10と互いに素でも合成数だと何か問題があるんでしょうか?
GAI さんからのコメントです。(平成29年7月5日付け)
らすかるさん、ご検証ありがとうございます。使い方の方法がまずかったですね。
上記の<方法>を変更して、
<新方法>
① Nの最下位を除いた残りでできる数+最下位の数*K(p)を新たにNとする。
② 上記の作業を繰り返す。
③ こうして桁数を小さくしたNに対し、N≡0 (mod p) になれば、元のNは素数pで割り切れる。
(例) N=1277613947なら、N=127761394+7*295=127763459、N=12776345+9*295=12779000
N=12779、N=1277+9*295=3932、N=393+2*295=983≡0 (mod 983)
→ 元のN=1277613947は、983で割れるの判断が可能
(しかし、実際元のNをそのまま983で割ってもあまり変わらない気もしますね。)
りらひいさんからのコメントです。(平成29年7月4日付け)
宇宙のかなたにある星「オク」。この星では八進法が使われている。桁数が多い整数Mが
あって、それがkの倍数かどうか判定したい。(k=2~7)どのような方法が簡単だろうか。
ただし、八進法の加算・減算は自在に使えることとし、桁数が小さければ乗算・除算もある
程度可能とする。
また、別の星「ドデ」では十二進法が使われている。星「オク」の場合と同様に、
k=2~B(十進法の11)の倍数判定法を考えてみてほしい。
・・・まあ、わたしは八進法や十二進法の加減乗除なんてすぐにできないので、判定法があっ
ても全然楽ではなくて意味がないのですが...。
DD++さんからのコメントです。(平成29年7月4日付け)
こうかな?
「オク」星人の考察
・2で割り切れるか・・・10が2で割り切れるので、下1桁が2で割り切れればよい。
・3で割り切れるか・・・10=3*3-1 なので、全ての桁を交互に足し引きした結果が3の倍数に
なればよい。
例:62357が3で割り切れるか→6-2+3-5+7=11は3の倍数なので、割り切れる
・4で割り切れるか
10が4で割り切れるので、下1桁が4で割り切れればよい。
・5で割り切れるか・・・最下位を切り取ってその2倍を前に足すのを繰り返し5になればよい。
例:1762が5で割り切れるか→176+2*2=202、20+2*2=24、2+4*2=12、1+2*2=5 なので割り切
れる
・6で割り切れるか・・・2の倍数かつ3の倍数であればよい。
・7で割り切れるか・・・全ての桁を合計して7の倍数になればよい。
例:37425が7で割り切れるか→3+7+4+2+5=25は7の倍数なので割り切れる
「ドデ」星人の考察
・2で割り切れるか・・・10が2で割り切れるので、下1桁が2で割り切れればよい。
・3で割り切れるか・・・10が3で割り切れるので、下1桁が3で割り切れればよい。
・4で割り切れるか・・・10が4で割り切れるので、下1桁が4で割り切れればよい。
・5で割り切れるか・・・最下位を切り取ってその3倍を前に足すのを繰り返し5かAになればよい。
・6で割り切れるか・・・10が6で割り切れるので、下1桁が6で割り切れればよい。
・7で割り切れるか・・・最下位を切り取ってその3倍を前に足すのを繰り返し7になればよい。
・8で割り切れるか・・・20が8で割り切れるので、10の位が2で割り切れて1の位が0か8、もしく
は10の位が2で割り切れなくて1の位が4ならよい。
・9で割り切れるか・・・30が9で割り切れるので、10の位が3で割り切れて1の位が0か9、10の
位を3で割った余りが1で1の位が6、10の位を3で割った余りが2で1の
位が3、のいずれかであればよい。
・Aで割り切れるか・・・2の倍数かつ5の倍数であればよい。
・Bで割り切れるか・・・全ての桁を合計してBの倍数になればよい。
「オク」星で新発見がありました。
・5で割り切れるか・・・2桁ずつ区切って交互に足したり引いたりして5の倍数になればよい。
例:1762が5で割り切れるか→17-62=-43は5の倍数なので割り切れる
例:5614320が5で割り切れるか→-5+61-43+20=31は5の倍数なので割り切れる
「ドデ」星でも新発見がありました。
・5で割り切れるか・・・2桁ずつ区切って交互に足したり引いたりして5の倍数になればよい。
例:7B63が5で割り切れるか→7B-63=18は5の倍数なので割り切れる
・7で割り切れるか・・・3桁ずつ区切って交互に足したり引いたりして7の倍数になればよい。
例:56789ABが7で割り切れるか→5-678+9AB=338=7*58なので割り切れる
りらひいさんからのコメントです。(平成29年7月4日付け)
流石です。わかりやすい説明をありがとうございます。一応私が用意していたものも書い
ておきますね。十進法でよく使われるものを一般化してまとめると、次のような感じになると
思います。
「整数Mがn進法表記で与えられているとき、Mがkの倍数であるかどうかを判別したい。」
[0] 互いに素な整数k1,k2を用いて k = k1 * k2 と分解できるとき、
Mがkの倍数 ⇔ Mがk1の倍数 かつ Mがk2の倍数
[1] kがn^tの約数のとき、
Mがkの倍数 ⇔ Mの下t桁がkの倍数
[2] kがn^t-1の約数のとき、
Mがkの倍数
⇔ Mを下の桁からt桁ずつ区切ってそれぞれt桁の数とみなし、各々を足し合わせた数が
kの倍数
[2'] kがn^t+1の約数のとき、
Mがkの倍数
⇔ Mを下の桁からt桁ずつ区切ってそれぞれt桁の数とみなし、各々を交互に足し引きした
数がkの倍数
[3] kがs*n^t-1の約数のとき、
Mがkの倍数
⇔ Mを下t桁とそれより上側に分けてそれぞれ数とみなし、下t桁をs倍したものを上側の数
に足した数がkの倍数
[3'] kがs*n^t+1の約数のとき、
Mがkの倍数
⇔ Mを下t桁とそれより上側に分けてそれぞれ数とみなし、下t桁をs倍したものを上側の数
から引いた数がkの倍数
※nとkがどんな数であっても、[1]または[2]または[0],[1],[2]の複合のいずれかが必ず適用で
きます。(しかし[2]のtが大きい場合など、必ずしも簡便になるわけではないですが。)
(例) 八進法、十二進法での例
DD++さんの「オク」星人の考察で、最終的に「5」にたどり着くものだけでなく、「17」に行き着
く場合もありますね。
また、「ドデ」星人の考察で、最終的に「7」にたどり着くものだけでなく、「2B」に行き着く場合
もありますね。
DD++さんからのコメントです。(平成29年7月4日付け)
あ、本当だ。
DD++さんからのコメントです。(平成29年7月5日付け)
[3] や [3'] は掛け算の方が割り算の方が楽だとか足し算の方が楽だという理由で「簡単」
なのであって、計算回数自体は普通に割るのとそんなにかわらないんですよね。
ということで、[0]、[1]、[2]、[2'] だけ使うことにしましょう。これらは t 桁の暗算がサラリと
できれば簡単に判定できます。
(繰り上がりで t+1 桁になった場合はもう一度繰り返せば t 桁でなんとかなります。特殊な
例外はあるかもしれませんが、そういうのは除いて考えてよいことにしましょう)
さて、各N進法で、全ての一桁の数について判定できるために何桁の暗算能力が必要か
考えてみることにします。
三進法:1桁
四進法:1桁
五進法:1桁
六進法:2桁(4の判定)
七進法:2桁(5の判定)
八進法:2桁(5の判定)
九進法:3桁(7の判定)
十進法:3桁(7と8の判定)
十一進法:3桁(7と9の判定)
十二進法:3桁(7の判定)
十三進法:5桁(Bの判定)
さて、この数列はこの先もずっと単調増加でしょうか、そうでもないでしょうか。