完全順列 
1 から n までの自然数の書かれたカードが n 枚ある。今そのカードをよく切って、下図の
ように番号順に置いていく。
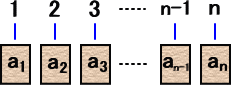
もし、
ak=k
となるような k が存在するとき、「出合い」が起こったといわれる。
このとき、出会いが全く起こらない数の並びを完全順列(または攪乱順列)という。
出合いが起こらない場合の数を F(n) とおくと、次の漸化式が成り立つ。
F(1)=0、F(2)=1、F(n)=(n−1)(F(n−1)+F(n−2))
この漸化式を解くと、
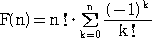
である。(→ 参考:「自然対数の底 e の体感」、「席替えの数理」)
当HPがいつもお世話になっているHN「GAI」さんが、平成22年7月10日付けで次の問題
を提起された。
男子3人、女子3人がそれぞれ一列ずつで席が決まって並んでいたとする。
これを席替えして、どの人も前の席からの位置が変わり、隣の異性も変わる並び方は、
の2通りしかない。そこで、問題である。
男、女それぞれ4人が一列で並んでいたのを並び替え、どの人も前の位置と違う場
所で、しかも隣の人も違う異性になる並び方が何通りあるだろうか。
完全順列の匂いがしたので解いてみた。
まず、男子の並び方は、F(4)=3(F(3)+F(2))=3(2+1)=9
(通り) ある。
BADC 、CADB 、DABC 、BDAC 、CDAB 、DCAB 、BCDA 、CDBA 、DCBA
例えば、BADC (Aの移動した先の人がAの移動前の位置にくる場合)について、女子の
並び方を考えよう。
a → 3番目 または 4番目 しかない。
a → 3番目 とすると、 b → 4番目 である。
このとき、 c → 1番目 または 2番目 で、d は残りに確定である。
a → 4番目 とすると、 b → 3番目 である。
このとき、 c → 1番目 または 2番目 で、d は残りに確定である。
よって、この場合の女子の並び方は、 cdab 、dcab 、cdba 、dcba の4通りある。
次に、CADB (Aの移動した先の人がAの移動前の位置に来ない場合)について、女子
の並び方を考えよう。
a → 3番目 または 4番目 しかない。
a → 3番目 とすると、 b → 1番目 である。
このとき、 c → 4番目 、d → 2番目である。
a → 4番目 とすると、 b → 1番目 または 3番目である。
b → 1番目 とすると、 解なし
b → 3番目 とすると、 c → 2番目 、d → 1番目である。
よって、この場合の女子の並び方は、 bdac 、dcba の2通りある。
以上から、求める場合の数は、 4×3+2×6=24 (通り) ある。
(コメント) 答えは合っていますかね?自信はないです...f(^^;)。
...と上記で書きましたが、既にこの問題は当HPの「お茶の時間」−「パズル&クイズ」
の中の「色の組合せ」で解決済みでしたね!24通りで正解です。
当HPがいつもお世話になっているFNさんからのご指摘(平成22年7月11日付け)まで
気がつきませんでした...f(^^;)。
もしかしたらFNさんは、私以上に当HPの内容を熟知されているかもしれないですね...。
また、GAI さんは、この問題を「男女 n 人ずつ」と一般化したときの並びの総数が、n
を用
いて具体的に書けるかどうかも問題にしている。
FNさんによれば、5人は真面目に考えればできそうだが、n人は絶望的に思えるとのこと。
私も同感です。
5人の場合を考えるとすると
| |
| 1 |
2 |
3 |
4 |
5 |
| 2 |
3 |
4 |
5 |
1 |
| 3 |
4 |
5 |
1 |
2 |
|
のように1行目は、12345、2行目、3行目は、12345の順列で各列がすべて異なるよう
な3行5列の配列は何通りあるか。
4人のときの解答をヒントにして誘導をつけてみました。
(1) 2行目が、23154 のとき何通りあるか。
(2) 2行目が、23451 のとき何通りあるか。
(3) 全部で何通りあるか。
当HPがいつもお世話になっているらすかるさんからの情報です。
(平成22年7月11日付け)
n=3、4、5、・・・の場合の数から、FNさんの問題(3)の解は、552通りとなる。
らすかるさんからの情報を道しるべに、FNさんの問題を考えてみよう。
(解) 完全順列の公式から、まず、2行目の順列は全部で、
F(5)=4(F(4)+F(3))=4(9+2)=44 (通り) ある。
実際に、
|
| 1 |
2 |
3 |
4 |
5 |
| 2 |
1 |
5 |
3 |
4 |
| 2 |
1 |
4 |
5 |
3 |
| 3 |
1 |
2 |
5 |
4 |
| 4 |
1 |
2 |
5 |
3 |
| 5 |
1 |
2 |
3 |
4 |
| 3 |
1 |
5 |
2 |
4 |
| 4 |
1 |
5 |
2 |
3 |
| 5 |
1 |
4 |
2 |
3 |
| 3 |
1 |
4 |
5 |
2 |
| 4 |
1 |
5 |
3 |
2 |
| 5 |
1 |
4 |
3 |
2 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 3 |
5 |
1 |
2 |
4 |
| 3 |
4 |
1 |
5 |
2 |
| 2 |
3 |
1 |
5 |
4 |
| 4 |
3 |
1 |
5 |
2 |
| 5 |
3 |
1 |
2 |
4 |
| 2 |
5 |
1 |
3 |
4 |
| 4 |
5 |
1 |
3 |
2 |
| 5 |
4 |
1 |
3 |
2 |
| 2 |
4 |
1 |
5 |
3 |
| 4 |
5 |
1 |
2 |
3 |
| 5 |
4 |
1 |
2 |
3 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 4 |
5 |
2 |
1 |
3 |
| 4 |
3 |
5 |
1 |
2 |
| 2 |
4 |
5 |
1 |
3 |
| 3 |
4 |
5 |
1 |
2 |
| 5 |
4 |
2 |
1 |
3 |
| 2 |
5 |
4 |
1 |
3 |
| 3 |
5 |
4 |
1 |
2 |
| 5 |
3 |
4 |
1 |
2 |
| 2 |
3 |
5 |
1 |
4 |
| 3 |
5 |
2 |
1 |
4 |
| 5 |
3 |
2 |
1 |
4 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 5 |
4 |
2 |
3 |
1 |
| 5 |
3 |
4 |
2 |
1 |
| 2 |
5 |
4 |
3 |
1 |
| 3 |
5 |
4 |
2 |
1 |
| 4 |
5 |
2 |
3 |
1 |
| 2 |
4 |
5 |
3 |
1 |
| 3 |
4 |
5 |
2 |
1 |
| 4 |
3 |
5 |
2 |
1 |
| 2 |
3 |
4 |
5 |
1 |
| 3 |
4 |
2 |
5 |
1 |
| 4 |
3 |
2 |
5 |
1 |
|
上記の表で赤字の場合は他の場合と異なり、2つの文字で自己完結していることに注意
しなければならない。
例えば、次の表から、その違いが理解されることだろう。
(各テーブルで、1行目は元の順列、2行目は男子の順列、3行目以降は女子の順列)
|
| 1 |
2 |
3 |
4 |
5 |
| 2 |
1 |
5 |
3 |
4 |
| 5 |
4 |
1 |
2 |
3 |
| 4 |
5 |
1 |
2 |
3 |
| 5 |
4 |
2 |
1 |
3 |
| 4 |
5 |
2 |
1 |
3 |
| 3 |
4 |
1 |
5 |
2 |
| 4 |
3 |
1 |
5 |
2 |
| 3 |
4 |
2 |
5 |
1 |
| 4 |
3 |
2 |
5 |
1 |
| 3 |
5 |
4 |
1 |
2 |
| 5 |
3 |
4 |
1 |
2 |
| 3 |
5 |
4 |
2 |
1 |
| 5 |
3 |
4 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 2 |
1 |
4 |
5 |
3 |
| 3 |
5 |
1 |
2 |
4 |
| 5 |
3 |
1 |
2 |
4 |
| 3 |
5 |
2 |
1 |
4 |
| 5 |
3 |
2 |
1 |
4 |
| 5 |
4 |
1 |
3 |
2 |
| 4 |
5 |
1 |
3 |
2 |
| 5 |
4 |
2 |
3 |
1 |
| 4 |
5 |
2 |
3 |
1 |
| 4 |
3 |
5 |
1 |
2 |
| 3 |
4 |
5 |
1 |
2 |
| 4 |
3 |
5 |
2 |
1 |
| 3 |
4 |
5 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 3 |
1 |
2 |
5 |
4 |
| 4 |
5 |
1 |
2 |
3 |
| 5 |
4 |
1 |
2 |
3 |
| 4 |
5 |
1 |
3 |
2 |
| 5 |
4 |
1 |
3 |
2 |
| 2 |
4 |
5 |
1 |
3 |
| 2 |
5 |
4 |
1 |
3 |
| 4 |
3 |
5 |
1 |
2 |
| 5 |
3 |
4 |
1 |
2 |
| 2 |
4 |
5 |
3 |
1 |
| 2 |
5 |
4 |
3 |
1 |
| 4 |
3 |
5 |
2 |
1 |
| 5 |
3 |
4 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 4 |
1 |
2 |
5 |
3 |
| 2 |
5 |
1 |
3 |
4 |
| 3 |
5 |
1 |
2 |
4 |
| 5 |
3 |
1 |
2 |
4 |
| 5 |
4 |
1 |
3 |
2 |
| 2 |
3 |
5 |
1 |
4 |
| 3 |
4 |
5 |
1 |
2 |
| 3 |
5 |
4 |
1 |
2 |
| 5 |
3 |
4 |
1 |
2 |
| 2 |
4 |
5 |
3 |
1 |
| 2 |
5 |
4 |
3 |
1 |
| 3 |
4 |
5 |
2 |
1 |
| 3 |
5 |
4 |
2 |
1 |
| 5 |
3 |
4 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 5 |
1 |
2 |
3 |
4 |
| 2 |
4 |
1 |
5 |
3 |
| 4 |
5 |
1 |
2 |
3 |
| 3 |
4 |
1 |
5 |
2 |
| 4 |
3 |
1 |
5 |
2 |
| 2 |
4 |
5 |
1 |
3 |
| 2 |
5 |
4 |
1 |
3 |
| 3 |
4 |
5 |
1 |
2 |
| 3 |
5 |
4 |
1 |
2 |
| 4 |
3 |
5 |
1 |
2 |
| 2 |
3 |
4 |
5 |
1 |
| 3 |
4 |
5 |
2 |
1 |
| 3 |
5 |
4 |
2 |
1 |
| 4 |
3 |
5 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 3 |
1 |
5 |
2 |
4 |
| 2 |
4 |
1 |
5 |
3 |
| 4 |
3 |
1 |
5 |
2 |
| 4 |
5 |
1 |
3 |
2 |
| 5 |
4 |
1 |
3 |
2 |
| 2 |
5 |
4 |
1 |
3 |
| 4 |
5 |
2 |
1 |
3 |
| 5 |
4 |
2 |
1 |
3 |
| 5 |
3 |
4 |
1 |
2 |
| 2 |
3 |
4 |
5 |
1 |
| 2 |
5 |
4 |
3 |
1 |
| 4 |
3 |
2 |
5 |
1 |
| 4 |
5 |
2 |
3 |
1 |
| 5 |
4 |
2 |
3 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 4 |
1 |
5 |
2 |
3 |
| 2 |
3 |
1 |
5 |
4 |
| 2 |
5 |
1 |
3 |
4 |
| 3 |
4 |
1 |
5 |
2 |
| 5 |
4 |
1 |
3 |
2 |
| 3 |
5 |
2 |
1 |
4 |
| 5 |
3 |
2 |
1 |
4 |
| 3 |
5 |
4 |
1 |
2 |
| 5 |
3 |
4 |
1 |
2 |
| 2 |
3 |
4 |
5 |
1 |
| 2 |
5 |
4 |
3 |
1 |
| 3 |
4 |
2 |
5 |
1 |
| 5 |
4 |
2 |
3 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 5 |
1 |
4 |
2 |
3 |
| 2 |
3 |
1 |
5 |
4 |
| 2 |
5 |
1 |
3 |
4 |
| 3 |
4 |
1 |
5 |
2 |
| 4 |
3 |
1 |
5 |
2 |
| 2 |
4 |
1 |
3 |
5 |
| 2 |
3 |
5 |
1 |
4 |
| 3 |
5 |
2 |
1 |
4 |
| 3 |
4 |
5 |
1 |
2 |
| 4 |
3 |
5 |
1 |
2 |
| 2 |
4 |
5 |
3 |
1 |
| 3 |
4 |
2 |
5 |
1 |
| 4 |
3 |
2 |
5 |
1 |
| 4 |
5 |
2 |
3 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 3 |
1 |
4 |
5 |
2 |
| 2 |
5 |
1 |
3 |
4 |
| 5 |
3 |
1 |
2 |
4 |
| 4 |
5 |
1 |
2 |
3 |
| 5 |
4 |
1 |
2 |
3 |
| 2 |
3 |
5 |
1 |
4 |
| 2 |
4 |
5 |
1 |
3 |
| 5 |
3 |
2 |
1 |
4 |
| 4 |
5 |
2 |
1 |
3 |
| 5 |
4 |
2 |
1 |
3 |
| 2 |
4 |
5 |
3 |
1 |
| 4 |
5 |
2 |
3 |
1 |
| 5 |
4 |
2 |
3 |
1 |
| 4 |
3 |
5 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 4 |
1 |
5 |
3 |
2 |
| 2 |
3 |
1 |
5 |
4 |
| 2 |
4 |
1 |
5 |
3 |
| 3 |
5 |
1 |
2 |
4 |
| 5 |
3 |
1 |
2 |
4 |
| 5 |
4 |
1 |
2 |
3 |
| 2 |
5 |
4 |
1 |
3 |
| 3 |
5 |
2 |
1 |
4 |
| 5 |
3 |
2 |
1 |
4 |
| 5 |
4 |
2 |
1 |
3 |
| 2 |
3 |
4 |
5 |
1 |
| 3 |
4 |
2 |
5 |
1 |
| 3 |
5 |
4 |
2 |
1 |
| 5 |
3 |
4 |
2 |
1 |
|
|
| 1 |
2 |
3 |
4 |
5 |
| 5 |
1 |
4 |
3 |
2 |
| 2 |
3 |
1 |
5 |
4 |
| 2 |
4 |
1 |
5 |
3 |
| 3 |
5 |
1 |
2 |
4 |
| 4 |
5 |
1 |
2 |
3 |
| 2 |
3 |
5 |
1 |
4 |
| 2 |
4 |
5 |
1 |
3 |
| 3 |
5 |
2 |
1 |
4 |
| 4 |
5 |
2 |
1 |
3 |
| 3 |
4 |
2 |
5 |
1 |
| 4 |
3 |
2 |
5 |
1 |
| 3 |
4 |
5 |
2 |
1 |
| 4 |
3 |
5 |
2 |
1 |
|
他の場合も同様で、したがって、求める場合の数は、
4×(5×12+6×13)=552(通り) となる。
上記の表から、FNさんの問題も明らかとなる。
(1) 2行目が、23154 のとき何通りあるか。・・・・・・12通り
(2) 2行目が、23451 のとき何通りあるか。・・・・・・13通り
(3) 全部で何通りあるか。・・・・・・552通り
上記では、FNさんの問題を「数え上げる」という、とても「泥臭い」方法で解いたわけだが、
もっと綺麗に解きたいという思いはあった。FNさんが、私のそんな思いに答えてくれた。
(平成22年7月12日付け)
(1) 2行目が、23154 のとき何通りあるか。
| |
| 1 |
2 |
3 |
4 |
5 |
| 2 |
3 |
1 |
5 |
4 |
| A |
B |
C |
D |
E |
|
D、E は、1、2、3 のどれかであるから、 3P2=6(通り)。
そのうちの1通り、例えば、D=2、E=3 とすると、B=1
と確定。残りの 4、5 はA、C の何れかに入る。
よって、求める場合の数は、 3P2×2!=12(通り) |
(2) 2行目が、23451 のとき何通りあるか。
| |
| 1 |
2 |
3 |
4 |
5 |
| 2 |
3 |
4 |
5 |
1 |
| 3 |
1 |
5 |
2 |
4 |
| 3 |
4 |
5 |
1 |
2 |
| 3 |
5 |
1 |
2 |
4 |
| 3 |
5 |
2 |
1 |
4 |
| 4 |
1 |
5 |
2 |
3 |
| 4 |
1 |
5 |
3 |
2 |
| 4 |
5 |
1 |
2 |
3 |
| 4 |
5 |
1 |
3 |
2 |
| 4 |
5 |
2 |
1 |
3 |
| 5 |
1 |
2 |
3 |
4 |
| 5 |
4 |
1 |
2 |
3 |
| 5 |
4 |
1 |
3 |
2 |
| 5 |
4 |
2 |
1 |
3 |
|
これは樹形図等を使ってすべて書きあげるのが一番
早い。
左表から、求める場合の数は、
全部で、13通り。
(3) 全部で何通りあるか。
1行目と2行目の対応を置換とみたとき、すべての文字が動かなければならない。すべて
の置換は何個かの巡回置換の積になるが、すべての文字を動かすということは、長さ5の
巡回置換(上記の問題の(2)のタイプ)か長さ3の巡回置換と互換(長さ2の巡回置換)の積
(上記の問題の(1)のタイプ)しかない。即ち、(12345)のタイプと(123)(45)のタイプで
ある。
ところで、(12345)のタイプは、5個の円順列なので、4!=24(通り)。
(123)(45)のタイプは、1、2、3 の選び方が、5C3=10(通り)で、それぞれ(123)と
(132)の2通りあり、20通り。互換は残った2つで決まるので1通り。よって、20通り。
以上から、求める場合の数は、 24×13+20×12=552(通り) (終)
FNさんによれば、6人の場合も同様で、123456の置換ですべての文字を動かすものは
次のどれかである。
長さ6の巡回置換・・・・・・・・・・・・・(123456)のタイプ
長さ4の巡回置換と互換の積・・・・(1234)(56)のタイプ
長さ3の巡回置換2個の積・・・・・・(123)(456)のタイプ
互換3個の積・・・・・・・・・・・・・・・・(12)(34)(56)のタイプ
この4つのタイプについて、それぞれが何通りあるか、そしてそれぞれの場合の3行目が
何通りあるかを求めなければならない。
やっかいなのは1つだけ、即ち、1番目のタイプの3行目の個数を数えること。5人のとき
の(2)に当たる問題。普通は樹形図等ですべて書くことになる。
6人のときを解くのに、「普通は樹形図等を作って数えることになる」と書きましたが、実は
(非常に難しいですが)計算で解けます。(平成22年7月13日付け)
123456 ABCDEFは123456の順列で左の配列において各列はすべて異なる。
234561 この条件を満たす3行6列の配列は何通りあるか。
ABCDEF
この問題は「Menage problem」あるいは「Probleme des menages」といわれる有名な
問題と同じになります。19世紀に出され、1934年に一般の場合の式が作られ、1943年に
始めて証明されたというから相当難しい問題です。次の問題です。
6組の夫婦を円形のテーブルに次の条件を満たすように着席させる並び方は何通り
あるか。
男女は交互に座り、夫婦は隣り合わない。
6組の夫婦を、Aa、Bb、Cc、Dd、Ee、Ff とし、まず、a、b、c、d、e、f を円形に間を1つ
ずつあけながら並べる。空いている席に、1、2、3、4、5、6 と名前をつける。
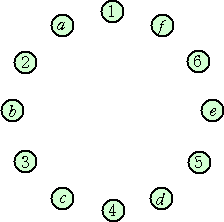
1、2、3、4、5、6 に、A、B、C、D、E、F を置くのだが、Aは1と2は駄目、Bは2と3は
駄目、・・・・・、Fは6と1は駄目。これはまさに上の問題の状況である。
6組の夫婦を n 組の夫婦としたものが、Menage problem である。
ただし、最初の問題では、A、B、C、D、E、F の並び方だけが問題だが、Menage
problem
では、a、b、c、d、e、f の並び方も数えるので結果は異なる。
「Menage problem」で検索すれば、たくさんヒットします。例えば下記のWikipedia。
http://en.wikipedia.org/wiki/M%C3%A9nage_problem
上の方に書いてある
12、96、3120、115200、5836320、382072320、31488549120、・・・
が男女とも動かした本来の Menage problem の解で、n の場合の式が、Mn でかいてある
ものです。
Menage numbers and ladies-first solutions のところに書いてある An が男女の片方を
固定したときの解の式で、具体的な数は、その下の
1、2、13、80、・・・
です。最初に書いた問題は、こちらのタイプで、80通りということになります。
(コメント) FNさんに感謝します。
GAI さんから問題をいただきました。(平成28年7月14日付け)
{1,2,3,4}を並べ替えたとき、元の位置にどの要素もあてはまらない並び方は、
2143、3142、4123、2413、3412、4312、2341、3421、4321
の9パターンが考えられる。(完全順列)
一般に異なるn個の要素を並べたとき、そのようになるパターン数f(n)は、
f(n)=(n-1)*(f(n-1)+f(n-2)),f(1)=0,f(2)=1
によって与えられる。(モンモール数)
そこで、{1,1,2,2,3,3}を勝手に並び替えたとき、どの要素も元の位置と異なるものになってい
るパターン数は?
さらに、{1,1,2,2,3,3,4,4,・・・・・,n,n}なら、そのパターン数は?
atさんからのコメントです。(平成28年7月16日付け)
n 種類の要素 1,2,3,・・・・・,n がそれぞれ m 個ずつあって、
{1,1,・・・,1,2,2,・・・,2,3,3,・・・,3,・・・・・・・・・・,n,n,・・・,n}
というふうに並んでいるとします。これら mn 個の要素を勝手に並び替えたとき、どの要素に
ついても、元の位置にあった要素とは異なる種類になっているような並べ方のパターン数を
A(n,m) とすると、
A(n,m)=(1/(m!))n(Σk=0〜mn (-1)k(mn-k))n)
A(n,2) の初めの10項は次のようになりました。
{A(n,2)}(n=1,・・・,10)
=[0, 1, 10, 297, 13756, 925705, 85394646, 10351036465, 1596005408152, 305104214112561]
(Maximaでの計算結果)
(A(n,2),n,1,5):[0, 1, 10, 297, 13756]
(A(n,3),n,1,5):[0, 1, 56, 13833, 6699824]
(A(n,4),n,1,5):[0, 1, 346, 748521, 3993445276]
(A(n,5),n,1,5):[0, 1, 2252, 44127009, 2671644472544]
(A(n,6),n,1,5):[0, 1, 15184, 2750141241, 1926172117389136]
(A(n,7),n,1,5):[0, 1, 104960, 178218782793, 1463447061709156064]
(コメント) {1,1,2,2,3,3}を勝手に並び替えたとき、どの要素も元の位置と異なるものになって
いるパターン数は、at さんの結果から、A(3,2)=10 となる。実際に並べてみると、
{3,3,1,1,2,2}、{2,2,3,3,1,1}、{2,3,1,3,1,2}、{3,2,1,3,1,2}、{2,3,1,3,2,1}、{3,2,1,3,2,1}、{2,3,3,1,1,2}、
{3,2,3,1,1,2}、{2,3,3,1,2,1}、{3,2,3,1,2,1}
(追記) GAI さんから、ご投稿いただきました。(令和3年12月13日付け)
「A000166」に載せられている完全順列(Derangements)数が、二項係数とガンマ関数との
組み合わせにより上手く計算されていくことに気付きました。
以下、その式と計算結果の様子です。
gp > F(n)=sum(i=0,n,(-1)^(n-i)*binomial(n,i)*gamma(i+1));
gp > for(n=1,20,print(n";"F(n)))
1;0.E-38
2;1.0000000000000000000000000000000000000
3;2.0000000000000000000000000000000000000
4;9.0000000000000000000000000000000000000
5;44.000000000000000000000000000000000000
6;265.00000000000000000000000000000000000
7;1854.0000000000000000000000000000000000
8;14833.000000000000000000000000000000000
9;133496.00000000000000000000000000000000
10;1334961.0000000000000000000000000000000
11;14684570.000000000000000000000000000000
12;176214841.00000000000000000000000000000
13;2290792932.0000000000000000000000000000
14;32071101049.000000000000000000000000000
15;481066515734.00000000000000000000000000
16;7697064251745.0000000000000000000000000
17;130850092279664.00000000000000000000000
18;2355301661033953.0000000000000000000000
19;44750731559645106.000000000000000000000
20;895014631192902121.00000000000000000000
以下、工事中


