席替えの数理 
4月に入学した高校生たちも、すっかり学校生活にも慣れ、当初の辺りを見渡す余裕もな
く緊張していた頃が懐かしい。「そろそろ席替えを!」という声があがるのも必然だ。
「まだ名前を覚えていないから...。」と抵抗するも、大抵の学校では、5月の中間テスト
明け位に席替えを行うところが多いのではないだろうか。
私の知り合いには、1回も席替えをしなかったという猛者もいるのだが、生徒側の「席替
え」を希望する真のねらいを考えると、思わず協力したくなるのも頷ける。
この席替えについて、福島工業高等専門学校の山野さんという方が面白い定理を提起さ
れている。
N人のクラスで席替えを行うとき、また同じ席になる人がいる場合がある。この席替
えを何回か行うと、同じ席になる人がいるときといないときがある。
しかし、この席替えを繰り返し行うとき、同じ席になる人は平均してちょうど1人であ
る。しかも、このことは、Nに依らない。
確かに、私のこれまでの経験からも、「あれっ!○○さん、席が前と同じだね!」ということ
が度々ある。そういうことが平均して一人はいるということのようだ。
この問題に関連して、次のような問題が直ぐ思い浮かぶ。
n人のクラスで席替えを行うとき、少なくとも1人が同じ席になる確率を求めよ。
これは、完全順列の考えと余事象の確率を用いて解決される。
完全順列については、当HPの中の「自然対数の底 e の体感」で述べられている。表現を
変えて再掲し、上記の問題を解いてみよう。
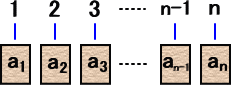 |
席替えする前に生徒は番号順に、1 から n まで
並んでいるものとする。そして、席替えをして、
a1、a2、・・・、an と並べ替えられたと考える。
もし、ak=k となるような k が存在するとき、席 |
替えしても席が変わらなかった生徒がいることになる。
そこで、誰も席が同じ生徒がいないような場合の数を F(n) とおく。この F(n) を実際に求
めてみよう。
F(n) は、1,2,3,・・・,n の数を並び替えたとき、先頭から数えた順番と数が一致するも
のが1つもない並べ方(完全順列または攪乱順列)の数に等しい。
数 1 は、a1 以外のどれかである。
今、数 1 が、ak (2≦k≦n)であるとする。このとき、次の2つの場合が考えられる。
(1) 数 k が、a1 であるとき、残りの n−2 個の数の並べ方の数は、F(n−2) 通り
(2) 数 k が、a1 でないとき、1 以外の n−1 個の数の並べ方の数は、F(n−1) 通り
したがって、次のような漸化式が成り立つ。
F(n)=(n−1)(F(n−1)+F(n−2))
明らかに、F(1)=0、F(2)=1 である。
このとき、 F(n)−nF(n−1)=−(F(n−1)−(n−1)F(n−2))
なので、
F(n)−nF(n−1)=(F(2)−2F(1))(−1)n=(−1)n
よって、
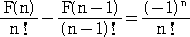
と変形できるから
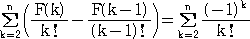
すなわち、

F(1)=0 なので、
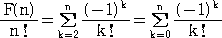
となる。
したがって、
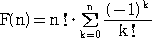
以上から、n人のクラスで席替えを行うとき、少なくとも1人が同じ席になる確率は、

となる。 ところで、
 |
なので、 |
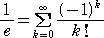 |
が成り立つ。 |
したがって、
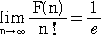
が成り立つので、n を限りなく大きくしたとき、上記の確率は、
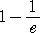
に近づく。表計算ソフトExcelで、”=EXP(−1)”により計算すると、
1/e =0.367879441171442・・・
であるので、席替えによって、少なくとも1人が同じ席になる確率は、n が十分大きいとき、
ほぼ、 0.632120558828557・・・ であると言える。
普通、席替えというとクラス内で行うのが通常なので、n=40 として、上記の確率を求
めてみよう。
F(40)=3.00158458444476×1047
40!=8.15915283247898×1047
なので、40人クラスの中で少なくとも一人が同じ席になる確率は、
0.632120558828557・・・
で、n を十分大きくした場合のものと比べ、ほぼ同じである。
ただ、この計算から、「少なくとも1人が同じ席になる」場合が起こりやすいことは理解で
きるが、実際問題として、「じゃ、何人くらいが同じになるの?」という問いかけに対しては
何も答えてはいない。この問いかけに明確に答えようというのが、冒頭に提起された定理
である。
数学においては、このような問題に対して、確率分布を考え、その期待値を計算するの
が筋だろう。
以下において、n 人のうち k 人だけが同じ席になる確率を、pk (0≦k≦n)とおく。
例(n=2 のとき) p0=1/2!=1/2 、 p1=0 、 p2=1/2!=1/2
よって、 このときの期待値は、 0×p0+1×p1+2×p2=1
例(n=3 のとき) p0=2/3!=1/3 、 p1=3C1・1/3!=1/2 、
p2=0 、 p3=1/3!=1/6
よって、 このときの期待値は、 0×p0+1×p1+2×p2+3×p3=1
例(n=4 のとき) p0=9/4!=3/8 、 p1=4C1・2/4!=1/3 、
p2=4C2・1/4!=1/4 、 p3=0 、 p4=1/4!=1/24
よって、 このときの期待値は、 0×p0+1×p1+2×p2+3×p3+4×p4
=0+1/3+1/2+0+1/6=1
例(n=5 のとき) p0=44/5!=11/30 、 p1=5C1・9/5!=3/8 、
p2=5C2・2/5!=1/6 、 p3=5C3・1/5!=1/12 、
p4=0 、 p5=1/5!=1/120
よって、 このときの期待値は、 0×p0+1×p1+2×p2+3×p3+4×p4+5×p5
=0+3/8+1/3+1/4+0+1/24=1
このように計算していくと、n の値によらず常に期待値は、1 であるような雰囲気である。
分散は、どうだろうか? n=5 のときに、実際に計算してみると、
(分散)=(02×p0+12×p1+22×p2+32×p3+42×p4+52×p5)−12
=3/8+2/3+3/4+5/24−1=1
「おやっ? 期待値も分散も、同じ値 1 になっている!」
試しに、n=4 のときも計算してみると、
(分散)=(02×p0+12×p1+22×p2+32×p3+42×p4)−12
=1/3+1+2/3−1=1
で、やはり、期待値も分散も、同じ値 1 になっている!
このように考えると、n 人のクラスで席替えを行うとき、X 人だけが席が同じであるような
確率分布 X は、少し特殊な分布のように思える。
平均と分散が同じ分布としては、ポアッソン分布が有名である。
ポアッソン分布は、2項分布 B(n ,p)において、平均 np(=m)を一定に保ちながら、n
の値を限りなく大きくしたときに得られる分布である。
n の値が十分大きく、np の値が一定なので、 p≒0 としてよい。このとき、分散は、
np(1−p)≒m で、平均と同じ値となる。
ポアッソン分布に従う確率変数 X は、0、1、2、・・・ という離散的な整数値をとり、
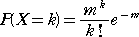
を満たすものである。
このとき、確率変数 X は、平均 m のポアッソン分布 Po(m) に従うとも言う。
ここで、ポアッソン分布が2項分布 B(n ,p)において、平均 np(=m)を一定に保ちなが
ら、n の値を限りなく大きくしたときに得られる分布であることを確認しておこう。
np=m とおくと、 n→∞ のとき、 p→0 で、
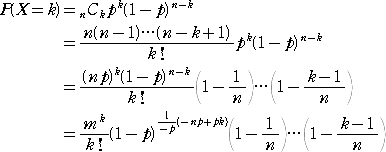
より、
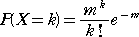
に近づく。よって、上記のことが確認された。
さて、n 人のうち k 人だけが同じ席になる確率を、pk (0≦k≦n)とおく。
このとき、 pk = P(X=k) = nCkF(n−k)/n! ( k≠n−1 )
pn−1 = 0 (← n−1人だけが同じということは起こらない!)
が成り立つ。ここで、
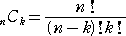 、
、 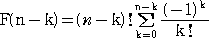
なので、
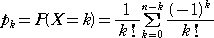
となる。 n の値を十分大きくとるとき、
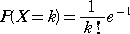
に近づく。このことから、n 人のクラスで席替えを行った場合、席が同じになる人数 X は、平
均 1 のポアッソン分布 Po(1) にほぼ従うことが分かった。
(P(X=n−1) = 0 を除いて!)
(追記) 令和4年5月23日付け
中間テストも終わり、そろそろ全国の学校で席替えが行われている頃だろう。
今、20人のクラス(男子10人、女子10人)で席替えが行われようとしている。座席は、下
図の通り、列毎に男女別になっている。

男子のA君と女子の a さんは4月以来隣同士で仲良しになり、A君は席替えしても a さん
の隣りに座りたいと考えている。
(1) 男子も女子も席替えする場合
(2) 男子は席替えしないで、女子だけが席替えする場合
A君は、a さんの隣りに座る確率を高くするために、(1)と(2)のどちらを選ぶべきだろうか。
(解)(1)の場合、確率は、 15×9!×9!/(10!×10!)=3/20
(2)の場合、確率は、
A君が男子列1にいる場合、 9!/10!=1/10
A君が男子列2にいる場合、 2×9!/10!=1/5
従って、A君が男子列1にいる場合は、(1)の場合を選択し、A君が男子列2にいる場合
は、(2)の場合を選択すると、a さんの隣りに座る確率が最も高くなる。
以下、工事中