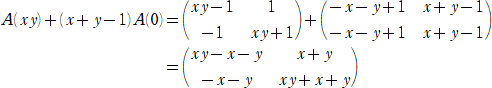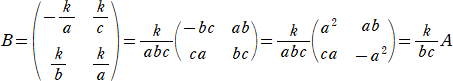�s��̕K�{�Z�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@���w�U�Ŋw�ԁu�w���E�ΐ��v�́A��U�������Ă��܂��ΈՂ����Ǝv����v�Z�����A�v�Z
�͂��R�����A�w�����I�o��������܂ł��܂�Ȃ������ꍇ�́A�ɒ[�ɓ���v�Z�Ǝv��
��悤�ŁA���k�͖��ӎ��̓��ɁA�u�Q���v���u�Q�|���� �� �v�Ƃ��Ă��܂������ł���B
�@����Ɠ����悤�Ȍ��ۂ��A���w�b�Ŋw�ԁu�s��v�ł��N����B�������m�̌v�Z�܂ł͓���
���͋N����Ȃ��̂����A�s�̂��̂��A�N���o�b�g�I�ɏ�������i�ɂȂ�ƁA�r�[��
�r���ɕ��鐶�k�������Ă���B
�@���Ƃ��A�Q���̐����s��
�@
���A �`2���` �����Ƃ��A���{�� �� �����|���� �̒l�����߂�B
�Ƃ������ŁA
�@
����A�A��������
�@��2�{���������@�A�@�����{���������@�A�@�����{���������@�A�����{��2����
�����A������A���{��
�� �����|����
�̒l�����߂邱�Ƃ͏��w�Ҍ����ɂ悭�s����v�Z��
����B
���ۂɌv�Z���Ă݂�ƁA�@�@�����{���������@�A�@�����{���������@���A
�@�i���{���|�P�j�����O�@�A�@�i���{���|�P�j�����O
�@���{�����P�@�̂Ƃ��A�@���������O
�@���̂Ƃ��A�@��2�����@�A�@��2�����@���A�@�����O�A�P�@�@�����O�A�P
�@���{�����P�@�Ȃ̂ŁA�@�i �� �C �� �j���i �O �C �O �j�A�i �P �C�P �j
�@����āA�@���{�����O�@�A�@�����|�������O�@�܂��́A�@���{�����Q�@�A�@�����|�������P
�@���{�����P�@�̂Ƃ��A�@�����|���������i�P�|���j�|���������|��2�|���������|�����O
�ȏォ��A�@�i ���{�� �C �����|���� �j���i �O �C �O �j�A�i �P �C �O�j�A�i �Q �C �P �j
�@�����A���̌v�Z�͏\����{�I�Ȃ̂����A�S����������A���������������o�����A����
���Z���ɂ͌���I�ɕs�����Ă���B�i�R���A���ꎟ���������A���w�T�̂Q�����̌���
�ň����邪�A�Q�����̌�����ނɂ��Ă���ȏ�A�A���������̌`�͓���ȏꍇ��
�����A����Ȃ鉞�p�͂����҂���͓̂���B���̏�ԂŊw�Ԙb�Ȃ̂ŁA��L�̌v�Z��
����Ɗ����鐶�k�������Ƒ����ɈႢ�Ȃ��B���̐ӔC�͕��ȏȂɕ����Ƃ����ł���B�j
�@��L�̌v�Z���������鐶�k�ɂƂ��āA��@�Ƀn�~���g���E�P�[���[�̒藝���g��������
�Ȃ�r���Łu�����I�v�ƍ��𓊂��Ă��܂����Ƃ͏\���\�z����邵�A�����ł�����B
�@�����A�n�~���g���E�P�[���[�̒藝�͍s��̌v�Z�ł͔��ɗL���Ȓ藝�Ȃ̂ŁA���̒�
���̍������s��w�K�̂ЂƂ̎R��ƌ����Ă������߂��ł͂Ȃ��悤�Ɏv���B
�@�n�~���g���E�P�[���[�̒藝��p����A���̂悤�ɉ������B
�@�s�� �` �ɑ��āA�@�`2�|�i���{���j�`�{�i�����|�����j�d���n�@�����藧�B
�@�`2���`�@�Ȃ̂ŁA�@�`�|�i���{���j�`�{�i�����|�����j�d���n
�@���Ȃ킿�A�@�@�i���{���|�P�j�`���i�����|�����j�d
�@���{�����P�@�̂Ƃ��A�@�����|�������O
�@���{�����P�@�̂Ƃ��A�@�`�����d�@�i��
�͒萔�j�@�Ƃ�����B�@�i���@�����̕������L�[�|�C���g�j
�@�`2���`�@�ɑ�����āA�@��2�d�����d�@���A�@��2�����@�@�@����āA�@�����O�A�P
�@�����O�@�̂Ƃ��A�@�`���n�@�@���̂Ƃ��A�@���{�����O�@�A�@�����|�������O
�@�����P�@�̂Ƃ��A�@�`���d�@�@���̂Ƃ��A�@���{�����Q�@�A�@�����|�������P
�@�@�ȏォ��A�@�i
���{�� �C �����|���� �j���i �O �C �O �j�A�i �P �C �O�j�A�i �Q �C �P
�j
�i�R�����g�j�@���̉�@�ɂ��đ��q�Ɋ��z������A�u�����邯��ǁA�Ȃ������肱�Ȃ�
�@�@�@�@�@�Ȃ��`�v�Ƃ̂��ƁB���������A�������Z���̍��A���̕s���ȉ�@�ɔY�L����
�@�@�@�@�@�h���Ă����D�D�D�B���ł́A�������R�ȉ�@�Ǝv���Ă���̂����B
�@�n�~���g���E�P�[���[�̒藝�́A�s��� �� ��̌v�Z�ȂǂɗL���ł���B
��@�Q���̐����s��
�@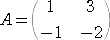
�ɂ��āA�@�`2�A�`3�A�`4�A�`10 ���v�Z����B
�@�n�~���g���E�P�[���[�̒藝���A�@�`2�{�`�{�d���O
����āA
�@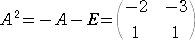
�@�܂��A�@�`3�|�d���i�`�|�d�j�i�`2�{�`�{�d�j���n�@���A�@�`3���d
���̂Ƃ��A�@�`4���`3�`���d�`���`�@�A�@�`10���i�`3�j3�`���d3�`���d�`���`
�i�R�����g�j�@���ʂɐ����v�Z���Ă����߂��邪�A��L�̕���������Ƃ�����ꂩ�ȁH
�@��L�̏ꍇ�́A���܂�n�~���g���E�P�[���[�̒藝�̉��b���������Ȃ����A���̖���
�͎����ł��邱�Ƃ��낤�B
��@�Q���̐����s��
�@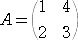
�ɂ��āA�@�`3�|�U�`2�{�S�`�{�T�d
���v�Z����B
�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�S�`�|�T�d���O
����āA
�@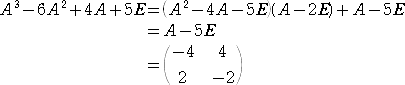
�i�R�����g�j�@�܂Ƃ��ɐ����v�Z���Ă��悢���A���̕��@�Ɋ���Ă��܂��Ɛ����v�Z��������
�@�@�@�@�@�@�Ȃ�͎̂������D�D�D�H
�@�n�~���g���E�P�[���[�̒藝�́A���Z�ł́A�Q���̐����s��Ɍ��肳��Ă���̂ŁA����
�ؖ��́A���ȏ��ł͐����v�Z�Ŋm���߂邱�ƂŏI�����Ă���B
�i�NjL�j�@�����Q�O�N�W���Q�R���t��
�@���������v�Z������ɂ��Ă��A���̂悤�Ȏ�@�����邱�Ƃ��ŋߒm�����̂ŏЉ�����B
������������F����ɂƂ��Ă͊��m�̎�@��������Ȃ����D�D�D�B
�i�n�~���g���E�P�[���[�̒藝�̏ؖ��j
�@�`2�|�i���{���j�`
���`�o�`�|�i���{���j�d�p�@�@�i���@���̂悤�Ȏ��ό`����肢�ł��ˁI�j
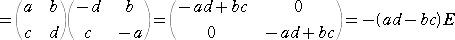
����āA�@�`2�|�i���{���j�`�{�i�����|�����j�d���n�@�����藧�B�@�i�؏I�j
�@�������A�n�~���g���E�P�[���[�̒藝�́A��ʂ� �� ���̐����s��ɂ��ď�ɐ��藧����
�ł���̂ŁA�����ł͈�O���N���A��ʂ� �� ���̐����s��ɂ��Ă��ȒP�ɁA���̏ؖ�����
���o����悤�ɁA��ʂ̐��`�㐔�w�ōs���Ă��闝�_���A�Q���̐����s��̘b�ɏĂ�����
�āA�����v�Z�ɂ��Ȃ��n�~���g���E�P�[���[�̒藝�̏ؖ����A���̃y�[�W�Ŏ��݂悤�Ǝv���B
�@�Q�l�ɂ����Ă��������������́A
�@�O��q�P�@���@�@������`�㐔�@�@�i�|���فj
�@��̓I�ȗ���肪�L�x�ŁA������₷�����K�`���̗Ǐ��ł���B
�i�O��搶�̌������͎��̏������錤�����̋߂��������̂ŁA�����A������ŁA������Ă��邩�ȁD�D�D�H�j
�@�ȉ��ŁA�s��͑S�āA�Q���̐����s��Ƃ���B
�@�s��
�@
�ɑ��āA�s�Ɨ�����ւ����s����A�]�u�s���Ƃ����A
�@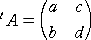
�ŕ\���B�]�u�s��ɂ��āA���̐��������藧���Ƃ͖��炩���낤�B
�@���i�`�{�a�j�����`�{���a�@�@�@�@���i�`�a�j�����a���`
�@�܂��A��x�N�g�����A
�@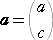 �@�@�@
�@�@�@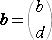
�Ƃ����ƁA�s�� �` �́A�@�`���i ���@�@�� �j�@�Ə�����B���̂悤�ȕ\�������A�s�� �` �������Ƃ�
���B��L�ł́A��x�N�g���ŕ������Ă��邪�A����������̏��s��ɕ������邱�Ƃ���
�肦��B
�@���̕����Ƃ����l�����́A���̂悤�ȏꍇ�ɂƂĂ��L���ł���B
�i�P�j�@�����ɁA�܂Ƃ܂��āu�O�v������Ƃ��ɁA�s��̐ς����߂�
�i�Q�j�@�����ɁA�܂Ƃ܂��āu�O�v������Ƃ��ɁA�s�����߂�
�i�R�j�@�ŗL�l�A�ŗL�x�N�g���𗘗p���āA�s��̑Ίp�������߂�
�@���w�Q�N�Ŋw�ԘA���P���������̉�@�̌����́A�u�����̏����v�ł���B���̕���Ƃ��āA
���w�ł́A�u����@�v�u�����@�v�u���u�@�v�Ȃǂ��w������Ă���B
�@���̎��ό`�ɋ��ʂ��錴���́A
�i�C�j�@�P�̎��ɁA�O�ȊO�̐����|���Ă����͕s��
�i���j�@���Ǝ������ւ��Ă����͕s��
�i�n�j�@�P�̎��ɁA���̎������{���������̂������Ă����͕s��
�ł���B�@���̌��������ƂɘA�����������������@���A�u�|���o���@�v�Ƃ����B
�@���̑|���o���@�́A�s��̗l���ŁA�Ȍ��ɕ\�������B���̍ۂɗp�����錴���́A��
�L�̌������s��̌��t�ɒu�������Ď��̂悤�Ȍ`�ƂȂ�B
�i�`�j�@�P�̍s�ɁA�O�ȊO�̐����|���Ă����͕s��
�i�a�j�@�s�ƍs�����ւ��Ă����͕s��
�i�b�j�@�P�̍s�ɁA���̍s�����{���������̂������Ă����͕s��
��@�A��������
�@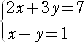
�������B
�i���j�@�|���o���@�ɂ��B
| �Q |
�R |
�V |
|
| �P |
�|�P |
�P |
|
|
|
|
|
| �T |
�O |
�P�O |
�E�E�E�@��Q�s���R�{�������̂��P�s�ɉ����� |
| �P |
�|�P |
�P |
|
|
|
|
|
| �P |
�O |
�Q |
�E�E�E�@��P�s���T�Ŋ��� |
| �P |
�|�P |
�P |
|
|
|
|
|
| �P |
�O |
�Q |
|
| �O |
�|�P |
�|�P |
�E�E�E�@��P�s���|�P�{�������̂��Q�s�ɉ����� |
|
|
|
|
| �P |
�O |
�Q |
|
| �O |
�P |
�P |
�E�E�E�@��Q�s���|�P�Ŋ��� |
�ȏォ��A���߂�������̉��́A�@�����Q�@�A�@�����P�@�ƂȂ�B
�@�s�� �` �ɑ��āA�@�`�a���a�`���d�@�ƂȂ�s�� �a �����݂���Ƃ��A�s�� �` �͋t�s�����
�Ƃ����A�a���`-1�@�ƕ\���B
�@��L�̑|���o���@�ɂ���@�́A�t�s���p����Ύ��̂悤�ɂȂ�B
�@�����ŁA
�@
�ɑ��āA���̋t�s�� �`-1 �́A
�@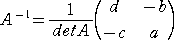
�i�������A�@�������`�������|���� �ł���B�j
�Ȃ̂ŁA
�@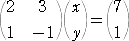
���A
�@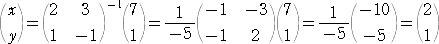
���Ȃ킿�A���߂�������̉��́A�@�����Q�@�A�@�����P�@�ƂȂ�B
�@��L�̑|���o���@�ɂ��A�W���s�� �` �͊Ȗ�āA�P�ʍs�� �d �ɂȂ��Ă���B��
�Ȃ킿�A�W���s�s��̊�{�ό`�i�`�j�i�a�j�i�b�j�ɂ��P�ʍs�� �d �ɊȖ��A�W
���s�� �` �͕K���t�s��������Ƃ�������B
�@�s�� �` �̋t�s��̌v�Z�ŁA�s�� �������` �̒l����ї]���q�̍l��������ł���B
�@�s��
�@
�ɑ��čs�� �������`�������|���� �ł��邪�A�u���̍l����p���Ď��̂悤�ɒ�`��������
�ł���B�i���@�Q�l�F�u���R�r�̒藝�v�j
�@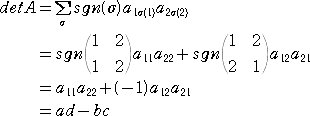
�@�������A�@������11�@�A������12�@�A������21�@�A������22�@�ŁA����ɁA
�@�������i�Ёj���i�|�P�j���@�i�� �́A�u�� �� ��\���݊��̐��j�@�Ƃ���B
�@���̍s�̐�Βl �b�������`�b�́A�Q�̗�x�N�g��
�@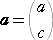 �@�@�@
�@�@�@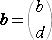
���������镽�s�l�ӌ`�̖ʐρb�����|�����b�ɓ��������Ƃ͋����[�����ʂł���B
�@
�@�s�̒�`���疾�炩�Ȃ悤�ɁA���̐��������藧�B
�i�P�j�@�s�Ɨ����ꂩ���Ă��A�s�̒l�͕s�ρi�s�Ɨ�Ɋւ��đΏ́j
�@�@���Ȃ킿�A�@������ �`�������� ���`
�i�Q�j�@�Q�̍s�i��j����ꂩ����ƁA�s�́A�|�P �{�ɂȂ�
�@�@�s�i��j�����ւ���ƁA���Ƃ̒u���Ɍ݊����V���ɏ悺����̂ŁA�����́A�|�P �{��
�@�Ȃ�B
�i�R�j�@�s�́A�e�s�i��j�Ɋւ��Đ��`�ł���
�i�S�j�@�P�̍s�i��j�̋��ʈ����́A�s�̊O�ɂ����肾����
�i�T�j�@�P�̍s�i��j�̗v�f���S�ĂO�Ȃ�A�s�̒l�͂O
�i�U�j�@�Q�̍s�i��j���������Ƃ��A�s�̒l�͂O
�@�@�������s�i��j�����ւ���ƁA�i�Q�j���A������ �`���|������ �` �Ȃ̂ŁA������ �`���O
���̂Ƃ��A�i�R�j�Ɓi�U�j����A
�i�V�j�@�P�̍s�i��j�ɔC�ӂ̐��������đ��̍s�i��j�ɉ����Ă��s�̒l�͕s��
�@�s�Ɋւ��āA���̒藝���悭�p������B
�@������ �`�a�������� �`�E������ �a
�@�Q���̐����s��ł́A�����v�Z�ɂ��m���߂��邪�A�����ł́A����ʓI�ȏꍇ�ɂ�
�ʗp����ؖ���^���Ă������B
�i�ؖ��j�@�܂��A�S���̐����s��̍s�ɂ��āA
�@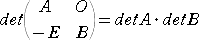
�����藧���Ƃ������B
�@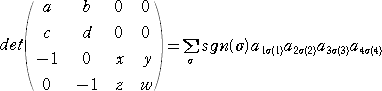
�ɂ����āA���ӂ̐����̏���A�ЂɊւ���a�́A
�@�Ёi�P�j���P�A�Ёi�Q�j���Q�@�@�܂��́@�Ёi�P�j���Q�A�Ёi�Q�j���P
�̏ꍇ�������l����悢�B���̂Ƃ��A
�@�Ёi�R�j���R�A�Ёi�S�j���S�@�@�܂��́@�Ёi�R�j���S�A�Ёi�S�j���R
���������āA�@�o �P �C �Q �p�̒u�����@�сA�@�o �R �C �S �p�̒u�����@�� �Ƃ���ƁA
�@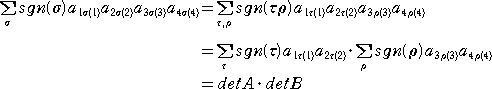
�����藧�B
�@���ɁA���ӂ̍s�ɂ����āA���̂悤�ȑ�����s���B
�@��P��� �� �A��Q��� �� ���|�������̂��R��ɉ�����
�@��P��� �� �A��Q��� �� ���|�������̂��S��ɉ�����
���Ȃ킿�A
�@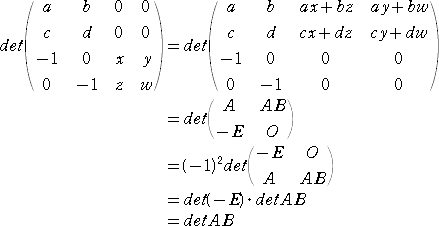 �i�؏I�j
�i�؏I�j
�@��L�ؖ��Ŏ��������Ƃ́A���낢��ȏ�ʂŊ��p�����B
�@�ǎ҂̂��߂ɗ��K�����c���Ă������B
���K����@�@���̓��������藧���Ƃ������B
�@
�@�܂��A���� ������ �`�a�������� �`�E������ �a�@�̗��K�����c���Ă������B
���K����@�@�`3���d�@�Ȃ�A�������`���P�@�ł��邱�Ƃ������B
�@���ɁA�]���q���`���悤�B
�@�Q���̐����s��`�ɑ��āA���̑� �� �s�� �� �����苎���ē�����s��̍s��
�i�|�P�j���{�� ���|�������̂��A�s��`����i���C���j�]���q�Ƃ����A�������ŕ\���B
�i��j�@�s��
�@
�ɂ��āA��11��(�|�P�j2�~�S���S�@�A�@��12��(�|�P�j3�~�R���|�R
�@��21���i�|�P�j3�~�Q���|�Q�@�A�@��22��(�|�P�j4�~�P���P
�@���̗]���q�̍l����p����ƁA�s�́A���̎��Ōv�Z�����B
�@�s��
�@
�ɑ��āA������ �`�����E��11�{���E��12�����E���{���E�i�|���j�������|�����@�ƂȂ�B
�@�s�� �` ���A���̂悤�ɕ\�����Ƃ��A�s�� �` ���]���q�W�J�Ƃ����B
�@�Q���̐����s��̏ꍇ�A���̓W�J�̉��b���邱�Ƃ͑S���Ȃ����A��荂���̍s��
�̌v�Z�ł͗L���ȕ��@�ƂȂ�B
�����ŁA
�@���E��11�{���E��12��������
�`�@�@�ł��邪�A�@���E��21�{���E��22�����E�i�|���j�{���E�����O
�Ƃ������������߂����Ȃ��B
�@�s��`�̑�i���C���j�]���q �������@��p���āA�]���q�s�� �`~
�@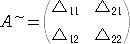
����`�����B�i�����̔z�u�ɒ��ӁI�j
���̂Ƃ��A�@���E��11�{���E��12�������� �`�@�@���E��21�{���E��22���O
�@���E��11�{���E��12���O�@�@�@�@�@���E��21�{���E��22�������� �`
�ł��邱�Ƃ���A�`�E�`~���`~�E�`���i������ �`�j�d�@�����藧���A������ �`���O�@�̂Ƃ��A
�@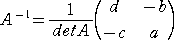
�ł��邱�Ƃ������ꂽ�B
�܂��A������ �i�`�E�`~�j���������`�E�������`~���������o�i������ �`�j�d�p���i������ �`�j2�@�ɂ����āA
������ �`���O�@�̂Ƃ��A�@�������`~�������� �`
������ �`���O�@�̂Ƃ��A�@�`���n�@�Ȃ�A�@�`~���n�@�Ȃ̂ŁA�@�������`~�������� �`
�@�`���n�@�Ȃ�A�@�`�E�`~���n�@���A�@�`~ �͋t�s��������Ȃ��B
�@���Ȃ킿�A�@�������`~���O�@�����藧���A�@�������`~�������� �`
�ȏォ��A����ɂ��Ă��A�@�������`~�������� �`�@�����藧�B
�i�R�����g�j�@���̓����͐����v�Z����Ζ��炩�����A��ʓI�ȏؖ����ӎ�����Ə�q�̂悤
�@�@�@�@�@�ɂȂ�B
�@�s�� �` ��p���āA�P���ϊ��@�s�i���j���`���@����`�����B
�@�P���ϊ� �s �ɂ����āA���̐��������藧�B
�@�s�i���{���j���s�i���j�{�s�i���j�@�@�@�s�i�����j�����s�i���j�@�@�i���͒萔�j
�@���̐�������A�@�s�i�O�j���O�@�ł���B���Ȃ킿�A�P���ϊ��ɂ��A���_�͌��_�Ɉڂ����B
�@�x�N�g�� �� �S�̂̏W���� �u �ŕ\���ƁA�u �́A�P���Ɨ��ȂQ�̃x�N�g�� ��1 �A ��2 �ɂ��
���������B
�@���̂Ƃ��A�s��̓����@�i �s�i��1�j�@�s�i��2�j �j���i ��1�@��2 �j�a�@�����s�� �a �����݂���B
���̍s�� �a �̂��Ƃ��A��� �o ��1 �C ��2 �p �Ɋւ���\���s��Ƃ����B
�i ��1�@��2 �j���d�@�̂Ƃ��A��� �o ��1 �C ��2 �p �͕W�����ƌ�����B
�@�W�����ɂ����ẮA�\���s�� �a �́A�`�@�ƈ�v����B
�@���܁A��� �o ��1 �C ��2 �p ��ʂȊ�� �o ���f1 �C ���f2 �p �ɕς��邱�Ƃ��l����B
�@�i ���f1�@���f2 �j���i ��1�@��2 �j�o�@�i�o�͐����s��j
���̂Ƃ��A�s�� �o �̂��Ƃ��A���̕ϊ��s��Ƃ����B
�@�P���ϊ� �s �̊�� �o ��1 �C ��2 �p �Ɋւ���\���s��� �` �A��� �o ���f1 �C ���f2 �p �Ɋւ�
��\���s��� �a �Ƃ���ƁA
�@�i �s�i��1�j�@�s�i��2�j �j���i ��1�@��2 �j�`�@�@�i �s�i���f1�j�@�s�i���f2�j �j���i ���f1�@���f2 �j�a
�����藧���A�@�i ���f1�@���f2 �j���i ��1�@��2 �j�o�@�ł���̂ŁA
�@�i �s�i���f1�j�@�s�i���f2�j �j���i ���f1�@���f2 �j�a���i ��1�@��2 �j�o�a
����A�@�i �s�i���f1�j�@�s�i���f2�j �j���s�i ���f1�@���f2 �j���s�i ��1�@��2 �j�o
�@�@�@�@���i �s�i��1�j�@�s�i��2�j �j�o���i ��1�@��2 �j�`�o
�@����āA�@�o�a���`�o�@���A�@�a���o-1�`�o�@�����藧�B
�@���̌����́A�s��̑Ίp���Ȃǂɉ��p�����B
��@�W�����ɂ����āA�P���ϊ� �s �̕\���s����A
�@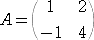
�Ƃ���B��� �o ���f1 �C ���f2 �p
�@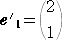 �@�@�@
�@�@�@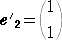
�Ɋւ���\���s�� �a �����߂�B
(���j�@��� �o ���f1 �C ���f2 �p �̕W�����Ɋւ���ϊ��s�� �o �́A
�@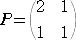
�ł���̂ŁA���߂�s�� �a �́A
�@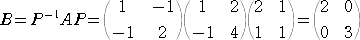
�i�R�����g�j�@��L�s��̑Ίp���� �Q ����� �R �́A�s�� �` �̌ŗL�l�ł���A���f1 �A���f2�@�́A
�@�@�@�@�@�����ɑ�����ŗL�x�N�g���i�̈�j�ł���B�i���@�Q�l�F�u�ŗL�x�N�g�������߂��v�j
�@�����s�� �` �ɑ��āA�@�f�`�i�Ɂj���������i�ɂd�|�`�j
���s�� �` ���ŗL�������Ƃ����B�@�������@�f�`�i�Ɂj���O�@�̉����ŗL�l�Ƃ����B
�@�ŗL�l �� �ɑ�����ŗL�x�N�g�� �� �i���O�j�́A�@�`���������@�ɂ�蓾����B
��@�s��
�@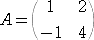
�̌ŗL�������́A�������i�ɂd�|�`�j���i�Ɂ|�P�j�i�Ɂ|�S�j�|�i�|�Q�j����2��T�Ɂ{�U
�@����āA�@��2��T�Ɂ{�U���i�Ɂ|�Q�j�i�Ɂ|�R�j���O�@���A�ŗL�l�́@�Q�@�Ɓ@�R
�ŗL�l �Q �ɑ�����ŗL�x�N�g���̈�́A�`�|�R�d �̗�x�N�g������A
�@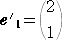
�ŗL�l �R �ɑ�����ŗL�x�N�g���̈�́A�`�|�Q�d �̗�x�N�g������A
�@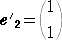
�ł��邱�Ƃ�����������B
��@���i�b����������-�g���������������j
�@�����s�� �` �̌ŗL������ �f�`�i�Ɂj�ɂ��āA�@�f�`�i�`�j���n�@�����藧�B
�@���̒藝�́A�s��
�@
�ɑ��āA�@�`2-�i���{���j�`�{�i�����|�����j�d���n
�Ə������������Z���ɂƂ��Ă͓���݂����邾�낤�B
�i�ؖ��j�@�a�����ɂd�|�`�@�Ƃ����ƁA�@������ �a�����������i�ɂd�|�`�j���f�`�i�Ɂj�@�Ȃ̂ŁA
�a���̗]���q�s�� �a��~ �ɂ��āA�@�a�� �a��~ ���f�`�i�Ɂj�d�@�����藧�B
�` �͂Q���̐����s��Ȃ̂ŁA �a��~ �́A�ɂɂ��č��X�P���̑������Ƃ��ď�����B
���Ȃ킿�A�@�a��~ ���ɂo�{�p�@�@�i�o�A�p �͂Q���̐����s��j�@�Ə�����B
���̂Ƃ��A�@�a�� �a��~ ���f�`�i�Ɂj�d�@�ɑ�����āA�@�i�ɂd�|�`�j�i�ɂo�{�p�j���f�`�i�Ɂj�d
�܂��A�f�`�i�Ɂj�́A�Q�����Ȃ̂ŁA�@�f�`�i�Ɂj����2�{���Ɂ{���@�i���A�� �͒萔�j
�Ə�����B�����ŁA�@�i�ɂd�|�`�j�i�ɂo�{�p�j����2�o�{�i�p�|�`�o�j�Ɂ|�`�p�@�Ȃ̂ŁA
�W�����r���āA�@�o���d�@�A�@�p�|�`�o�����d�@�A�@�|�`�p�����d�@�����藧�B
���̂Ƃ��A�@�@���`���`�i�p�|�`�o�j���`�p�|�`2�o�@�A�@���d���|�`�p�@�Ȃ̂ŁA
�`2�{���`�{���d���`2�{�i�`�p�|�`2�o�j�{�i�|�`�p�j���`2�{�`�p�|�`2�|�`�p���n
�ƂȂ�A����́A�@�f�`�i�`�j���n�@�����藧���Ƃ��Ӗ�����B�@�i�؏I�j
�i�R�����g�j�@��L�ł͂�≓���̌v�Z���s���Ă��邪�A�]���q�s��̐�������A�o�A�p ��
�@�@�@�@�s�� �` �ƌ����\�ł��邱�Ƃ�������̂ŁA�ϐ� �� �ɍs�� �` �������邱�Ƃ͉�
�@�@�@�@�\�ł���B���̂Ƃ��A �f�`�i�`�j���n�@�ł��邱�Ƃ́A�قƂ�ǎ������낤�B
�@�@�@�@�i�����ɂ��ؖ��Ɣ�r���āA���̏ؖ������Z�������ɍs�����Ƃ͖��d�ł��ˁI�j
�@�������ہA�s�̃ɂɑ������̂ł͂Ȃ��A�������W�J���ꂽ�ɂɑ������Ƃ�����
���͑�ł��낤�B
�@��L�ŁA�s��� �� ��̌v�Z�ɁA�n�~���g���E�P�[���[�̒藝���L���ł��邱�ƁA�����āA
���̎��ۂ̌v�Z����q�ׂ��B
�@�s��� �� ��̌v�Z�́A�s��̑Ίp���ɂ���čs���̂��ʏ킾�낤�B�Q������m���̌v
�Z���ɂ����p����A������Ɍv�Z�Z�p�̒����Ă���_�ŕK���K�����ׂ��Z�@�̈��
���ƌ�����B
�@���̗��_�I�w�i�ł́A�Ίp�s��
�@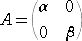
�ɂ��āA
�@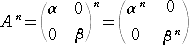
�Ƃ��������̐��藧�Ƃ��낪�傫���B
�@�����āA�i�o-1�`�o�j�����o-1�`���o�@�����藧���Ƃ���A�s��`�� �� �� �`�� �́A
�@�`�� ���o�i�o-1�`�o�j���o-1
�ɂ�苁�߂���B
��@�s��
�@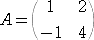
�̌ŗL�l�́@�Q�@�Ɓ@�R�@�ŁA�ŗL�l �Q �ɑ�����ŗL�x�N�g���̈�́A
�@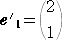
�ŗL�l �R �ɑ�����ŗL�x�N�g���̈�́A
�@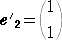
�ł��邱�Ƃ���L�Ōv�Z�����B
�@���̂��Ƃ���A�@�`���f1���Q���f1�@�A�@�`���f2���R���f2 �Ȃ̂ŁA�`�i���f1�@���f2�j���i�Q���f1�@�R���f2�j
���Ȃ킿�A
�@
������A�s�� �` �́A
�@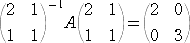
�ƑΊp�������B����āA�s�� �` �� �� ��́A
�@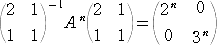
����A
�@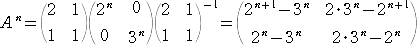
�Ƌ��߂���B
�@���̂��Ƃ����p���āA�A���^�̑Q����
�@��1���P
�A��1���P �A����+1�������{�Q����
�A����+1���|�����{�S����
�̉��́A�@�������i�Qn�|�R��-1�j�{�i�Q�E�Rn-1�|�Q���j���Rn-1
�@�������i�Qn-1�|�R��-1�j�{�i�Q�E�Rn-1�|�Q��-1�j���Rn-1
�ƂȂ�B
�i�R�����g�j�@���ݒ肪���������܂����I�@��1���P�A��2���R�A��3���X�A��4���Q�V�A�E�E�E�@������A
�@�@�@�@�@�������Rn-1�@�������ɕ������Ă��܂��āA��L�̍s��� �� ��̌v�Z�̗L���݂��`
�@�@�@�@�@���Ȃ��悤�ȁD�D�D�\���I
�@�b����������-�g�������������� �̒藝�@�F�@�`2-�i���{���j�`�{�i�����|�����j�d���n�@�ɂ����āA
�@�����|������������ �`�@�@�i�s�� �` �̍s�j
�ł��邪�A���{�����s�� �`�@����ȊT�O�ł���B
�@�s�� �` ���g���[�X�܂��́A�r������ �`�i�V���v�[���`�j�ȂǂƌĂ��B
�@���Z���ɑ��ē��ʂɋ������邱�Ƃ��Ȃ����Ƃ�m���Ă��m�炸���A�s��
�` �̐����Ɋ�
���������肪�U�������B
�s�� �` �̐���
�i�P�j�@�s���i�`�{�a�j���s�� �` �{ �s�� �a
�i�ؖ��j
�@ �@�@�A�@
�@�@�A�@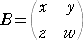
�ɑ��āA�@�s���i�`�{�a�j�����{���{���{�������{���{���{�����s�� �` �{�s�� �a�@�@�i�؏I�j
�i�Q�j�@�s���i���`�j�����E�s�� �`
�i�ؖ��j
�@ �@
�@
�ɑ��āA�@�s���i���`�j�������{���������i���{���j�����E�s�� �`�@�@�i�؏I�j
�i�R�j�@�s���i�`�a�j���s���i�a�`�j
�i�ؖ��j
�@ �@�@�A�@
�@�@�A�@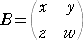
�ɑ��āA�@�s���i�`�a�j�������{�����{�����{�����@�A�s���i�a�`�j�������{�����{�����{����
����āA�@�@�s���i�`�a�j���s���i�a�`�j�@�����藧�B�@�@�i�؏I�j
�@�s�� �` �̐����Ƃ��ẮA��L�́i�P�j�i�Q�j�i�R�j���{���I�ł���B
���Ȃ킿�A�t�ɁA�Q���̐����s��S�̂�������S�̂ւ̎ʑ� �e �ŁA
�i�@�j�@�e�i�`�{�a�j���e�i�`�j�{�e�i�a�j
�i�A�j�@�e�i���`�j�����E�e�i�`�j
�i�B�j�@�e�i�`�a�j���e�i�a�`�j
�������̂́A�@�e�i�`�j�����E�s�� �`�@�i���͒萔�j�@�Ə����邱�Ƃ��m���Ă���B
�i�S�j�@�s���i�o-1�`�o�j���s�� �`
�i�ؖ��j�@�s���i�o-1�`�o�j���s���i�`�o�o-1�j���s�� �`�@�@�i�؏I�j
�@�i�S�j�̐����́A�������i�o-1�`�o�j�������� �`�@�ƕ����āA�s��̑Ίp���@�a���o-1�`�o�@�̌�
�Z�ɗp�����A�v�Z���P���ł���̂ŏd��ł���B
�i�T�j�@�s���i�`2�j�|�i�s�� �`�j2�{�Q������ �`���O
�i�ؖ��j�@�`2�|�i�s�� �`�j�`�{�i������ �`�j�d���n�@���A�s���o�`2�|�i�s�� �`�j�`�{�i������ �`�j�d�p���O
�����i�P�j�i�Q�j���A�@�s���i�`2�j�|�i�s�� �`�j�i�s�� �`�j�{�Q�i������ �`�j���O
���Ȃ킿�A�@�s���i�`2�j�|�i�s�� �`�j2�{�Q�i������ �`�j���O�@�@�i�؏I�j
�@��L�̐����̗��K���Ƃ��āA�Q�O�O�P�N�x�@��t��w�̓�����肪�œK�ł��낤�B
��@���@�Q���̐����s�� �` �A�a ���A�`���`�a�|�a�`�@�����Ƃ��A�@�`2���n�@�ł���
�@�@�@�@���Ƃ������B
�i���j�@�s���i�`�j���s���i�`�a�|�a�`�j���s���i�`�a�j�|�s���i�a�`�j���O�@�ŁA����ɁA
�@�`2���`�E�`���`�i�`�a�|�a�`�j���`2�a�|�`�a�`�@���A
�@�s���i�`2�j���s���i�`2�a�|�`�a�`�j���s���i�`2�a�j�|�s���i�`�a�`�j���s���i�`2�a�j�|�s���i�`2�a�j���O
����āA�@�s���i�`2�j�|�i�s�� �`�j2�{�Q�i������ �`�j���O�@���A�@������ �`���O�@�ƂȂ�B
�@�b����������-�g�������������� �̒藝���A�@�`2�|�i�s�� �`�j�`�{�i������ �`�j�d���n�@�Ȃ̂ŁA
�@�s���i�`�j���O�@�A�@������ �`���O�@���A�@�`2���n�@�ł��邱�Ƃ�������B�@�i�I�j
�i�R�����g�j�@�g���[�X�̐����������ɖ��킦��ǖ�ł��ˁI�P�ɁA�`���`�a�|�a�`�@����A����
�@�@�@�@�I�� �`2 ���v�Z���Ă��܂��Ă͘H���ɖ����Ă��܂��܂��D�D�D�B
�@���́A�����Q�P�N�x�@�������ȑ�w�̓������ł���B�����ł���L�Ŋm�F���� �s�� �`
�̐��������ʓI�ɗp�������ł���B�i��蕶�͋L�q�`���ɉ���I�j
��@���@�Q���̐����s�� �w�A�` �ɑ��āA �w3���`�@�ŁA�s�� �w �������ƂȂ�悤�ɁA
�@�@�@�@�w ���߂�B�������A
�@�@
�Ƃ���B
(���j�@������ �w3 ���i������ �w�j3�������� �`���P�S�{�T�O���U�S�@���A�@������ �w���S
�b����������-�g�������������� �̒藝�ɂ����āA�@�s�� �w �� ���@�Ƃ����ƁA
�@�w2�|���E�w�{�i������ �w�j�d���n�@�@���Ȃ킿�A�@�w2 �� ���E�w�|�S�d
���̂Ƃ��A�@�@�w3 �� ���E�w2�|�S�w�@���A�@�`�����E�w2�|�S�w���i��2�|�S�j�w�|�S���d
����āA�@�s�� �` ���s�� �i�i��2�|�S�j�w�|�S���d�j���i��2�|�S�j�E�s�� �w �|�W������3�|�P�Q���@����A
�@��3�|�P�Q�� �� �|�X�@�@���Ȃ킿�A�@��3�|�P�Q�� �{�X���O
���̂R���������́A�R�̎������������A���̂����̐������́A�R �݂̂ł���B
���������āA�@�� �� �s�� �w �� �R�@�ƂȂ�B
���̂Ƃ��A�@�`���T�w�|�P�Q�d�@���A�@�w���i�P/�T�j�iA�{�P�Q�d�j�@�ł���̂ŁA
�@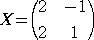
�ƂȂ�B�@�@�i�I�j
�i�R�����g�j�@���̖����A�s�� �w �̐����ɒ��ڂ��Ȃ��ƁA���C�������悤�Ȍv�Z�̗��Ɋ�������
�@�@�@�@�@�ꂻ���ȁD�D�D�\���I
�@���g�o�����������b�ɂȂ��Ă���r�i�g�j���ޑ�����������ꂽ�̂ŁA�����Ă݂�
���Ƃɂ��悤�B�i�����Q�P�N�Q���P�S���t���j
�@�r�i�g�j����̖��ݒ�ł͍s��̐����f���܂łƂ��Ă��邪�A�����ł́A�����͎���
�܂łƂ��Ă������B
�i�P�j�@�s��
�@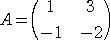
�ɑ��āA�w4 ���`�@�ƂȂ�s�� �w �����߂�B
�i���j�@������ �w4 ���i������ �w�j4�������� �`���|�Q�{�R���P�@���A�@������ �w���P�A�|�P
�i�C�j�@������ �w���P�@�̂Ƃ��A
�@�b����������-�g�������������� �̒藝�ɂ����āA�@�s�� �w �� ���@�Ƃ����ƁA
�@�w2�|���E�w�{�i������ �w�j�d���n�@�@���Ȃ킿�A�@�w2 �� ���E�w�|�d
�@���̂Ƃ��A�@�@�w4 �� ��2�E�w2�|�Q���E�w�{�d�@���A
�@�`����2�E�w2�|�Q���E�w�{�d����2�E�i���E�w�|�d�j�|�Q���E�w�{�d���i��3�|�Q���j�w�{�i�P�|��2�j�d
�@����āA�@�s�� �` ���s�� �i�i��3�|�Q���j�w�{�i�P�|��2�j�d�j���i��3�|�Q���j���{�Q�i�P�|��2�j����4�|�S��2�{�Q
�@����A��4�|�S��2�{�Q �� �|�P�@���Ȃ킿�A�@��4�|�S��2�{�R���O�@���A�@�����}�P�A�}
�@�����ŁA�@�� �� �s�� �w �� �P�@�̂Ƃ��A�@�`���|�w�@���A�@�w���|�`
�@�� �� �s�� �w �� �|�P�@�̂Ƃ��A�@�`���w�@���A�@�w���`
�@�� �� �s�� �w ��  �@�̂Ƃ��A�@�`��
�@�̂Ƃ��A�@�`�� �w�|�Q�d�@���A
�w�|�Q�d�@���A
�@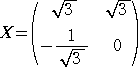
�@�� �� �s�� �w �� �| �@�̂Ƃ��A�@�`��
�@�̂Ƃ��A�@�`�� �w�{�Q�d�@���A
�w�{�Q�d�@���A
�@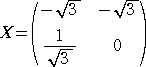
�i���j�@������ �w���|�P�@�̂Ƃ��A
�@�b����������-�g�������������� �̒藝�ɂ����āA�@�s�� �w �� ���@�Ƃ����ƁA
�@�w2�|���E�w�{�i������ �w�j�d���n�@�@���Ȃ킿�A�@�w2 �� ���E�w�{�d
�@���̂Ƃ��A�@�@�w4 �� ��2�E�w2�{�Q���E�w�{�d�@���A
�@�`����2�E�w2�{�Q���E�w�{�d����2�E�i���E�w�{�d�j�{�Q���E�w�{�d���i��3�{�Q���j�w�{�i�P�{��2�j�d
�@����āA�@�s�� �` ���s�� �i�i��3�{�Q���j�w�{�i�P�{��2�j�d�j���i��3�{�Q���j���{�Q�i�P�{��2�j����4�{�S��2�{�Q
�@����A��4�{�S��2�{�Q �� �|�P�@���Ȃ킿�A�@��4�{�S��2�{�R���O
�@���̂S���������͎������������Ȃ��̂ŕs�K�B�@�@�i�I�j
�i�Q�j�@�s��
�@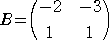
�ɑ��āA�w5 ���a�@�ƂȂ�s�� �w �����߂�B
�i�R�j�@�s��
�@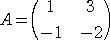
�ɑ��āA�w7 ���`�@�ƂȂ�s�� �w �����߂�B
�i�R�����g�j�@�i�Q�j�i�R�j�������i�P�j�Ɠ��l�ɂł���Ǝv���̂ŁA�ǎ҂̕��̗��K���ɂ��Ă������B
�i�NjL�j�@�����Q�V�N�P���P�R���t��
�@�s��̗��_�ɂ��āA���g�o�ǎ҂̂g�D�e�D�����胁�[���ɂĂ��낢��A�h�o�C�X�������B
�@�g�D�e�D����ɂ��A
�@�wn ���`�@�AA��E�@�̂Ƃ��AX�̑S�Ẳ��́A�ő�� n2����
�Ƃ̂��Ƃł���B�i���@�Q�l�F�u�������ʂ̊w�I�\���v�j
�@�s��� �� ��ɂ��Ă͎��̌������m���Ă���B�i����������̂Ŋo����K�v�͂Ȃ��I�j
�@�s��
�@
�ɂ����āA�b����������-�g�������������� �̒藝���A�`2-�i���{���j�`�{�i�����|�����j�d���n
�����藧�B�Q���������@��2-�i���{���j���{�i�����|�����j���O�@�̂Q�̉����A�� �A�� �Ƃ����B
�@���̂Ƃ��A
�i�P�j�@�������i�d���j�̂Ƃ��A�`����������-1�`�|�i���|�P�j�����d
�i�Q�j�@�������@�̂Ƃ��A
�@�`�����o�i�����|�����j/�i���|���j�p�`�|�����o�i����-1�|����-1�j/�i���|���j�p�d
�����藧�B
�@���g�o�ǎ҂̂g�m�u�|�e�g�v����̎���ł��B�i�����Q�T�N�W���Q�Q���t���j
�@�Q���̐����s��`�A�a�ɑ��āA�`�a���a�`���d �̂Ƃ��A�a���`�̋t�s����ĂԁA�Ƃ�������
���āA��`�a���d�@�Ȃ�@�a�`���d�ƂȂ�B��Ƃ���A���̏ؖ����킩��܂���B�Ȃɂ��ǂ�
����������������������B
�@���݁A���w�ւ̐��w�i�ʏ̍��㐔�j��A����`�㐔�w�i��v�ۏ��v���j���ǂ�ōl���Ă�
�܂����A�����Ōv�Z���悤�Ƃ���ƕ�����8��o�Ă��Ă���A�����ɍ����Ă��܂��i�������A��
�㐔�ł͂Q�������s��ł̏ؖ��͍��Z���ł��\�Ɠǂ߂�L�q������A���ꂩ�炷��Ɛ�
���𗘗p���邱�Ǝ��̂͊Ԉ���Ă��Ȃ��̂����Ǝv���Ă��܂��B�ǂ����������肢�܂��B
�@�Ƃ���ŁA�P�[���[��n�~���g���̒藝��p���邱�Ƃɂ��A�s��`�Ƃ����Ăd�ƂȂ�s��͈�
�ӓI�Ɍ��܂�̂ŁA����Ď����ꂽ�Ƃ����_�ő��v�Ƃ����l���Ɏ���܂����B
�@���Ȃ킿�A�`���ia b c d)�@�Ƃ����B�i�� ����A�E��A�����A�E�� �Ɠǂ�ł��������j
���̂Ƃ��A�P�[���[��n�~���g���̒藝���A �`2�|(���{��)A�{(�����|����)E���n
����āA�����|�������O �̂Ƃ��A�������������āA���ӂ� �����|���� �Ŋ���A�ؖ�����Ƃ�������
�ł��B�s��ɂ��Ă��Ȃ���ł���A�_�Ɍ�������C�����ĂȂ�܂���B��]�����肢
���܂��B
�@����̎�|�́A�u�Q���̐����s��`���t�s������v���Ƃ̒�`�Ƃ��āA
�i�P�j�@�Q���̐����s��a�����݂��ā@�`�a���a�`���d �����藧�Ƃ�
�Ƃ���̂��A���邢�́A
�i�Q�j�@�Q���̐����s��a�����݂��ā@�`�a���d �����藧�Ƃ�
�Ƃ���̂��ł��ˁB�i�Q�j�̏ꍇ�́A�u�`�a���d�@�Ȃ�@�a�`���d��������菇���c����܂��B
�@���`�㐔�w�̏��Ђł͑�́A�t�s��a�Ȃ���̂��\�����Ă݂��āA���̑��݂�ۏ��Ă�
��悤�ł��B���Ȃ킿�A
�@�Q���̐����s��`�ɑ��āA���̗]���q�s����`~�Ƃ���ƁA�@�`�E�`~���`~�E�`���i�������`�j�d
�����藧�̂ŁA�@�������`���O�@�̂Ƃ��A�@�a���i�P/�������`�j�`~�@�Ƃ����ƁA�@�`�a���a�`���d
�@����āA�������`���O�@�̂Ƃ��A�`�̋t�s��͑��݂��āA�`�̋t�s��́A�i�P/�������`�j�`~
�@�`�a���d�@���邢�́@�a�`���d�@�̂Ƃ��A�K�R�I�Ɂu�������`���O�v�Ȃ̂ŁA�`�̋t�s��͑��݂���
���B����āA�t�s���݂����`�Ƃ��āA�i�P�j�ł��i�Q�j�ł��ǂ����ł��n�j�Ƃ������ƂɂȂ��
�����A�����́A�����Ɂu�`�a���d�@�Ȃ�@�a�`���d��ł��邱�Ƃ����������Ǝv���܂��B
�i�ؖ��j�@�Q���̐����s��a�����݂��ā@�`�a���d �����藧�Ƃ��A�`�͋t�s������Ƃ���B
�@���̂Ƃ��A�@�������a���O�@�Ȃ̂ŁA�a���t�s������B���Ȃ킿�A����b�����݂��āA�a�b���d
����āA�@�a�`���a�`�d���a�`�a�b���a�d�b���a�b���d�@�ƂȂ�B
�@���������āA�@�`�a���d�@�Ȃ�@�a�`���d�@�ł���B�@�@�i�؏I�j
�@�|�e�g����̃R�����g�ł��B�i�����Q�T�N�W���Q�R���t���j
�@��Âɍl������A�`�a���d����������i�K�ŁA�`�͋t�s��������Ƃ��m�肷���ł��ˁB
���������āA���̋^��́A
�@��`�a���d�Ȃ�A�s��`�͋t�s������B�Ƃ���ŁA���̂Ƃ��b�`���d�����s��b�͂a��
�O�ɑ��݂���̂��H�
�Ƃ������ƂɂȂ��ł��ˁB�����l����ƁA��L�̂��Ƃ������Ɨ����ł��܂����B���肪�Ƃ�����
���܂����B
�i�R�����g�j�@��ʂ̑㐔�ł́A�u���������@�Ȃ�@���������v�Ƃ������Ƃ͌����Ȃ��̂ł����A����
�@�@�@�@�@�@�s��̏ꍇ�͌������ł��ˁI
�@�Ƃ���ŁA�`�a���d�@�̂Ƃ��A�b�`���d�ƂȂ�b�����݂���A����͂a�ȊO�ɂ���܂���B
���ۂɁA�@�b���b�d���b�`�a���d�a���a�@������ł��B
�@�����ł́A�b�`���d�ƂȂ�b�����݂���Ɖ��肵�Ď����Ă��܂����A���̑��݂�ۏ��Ȃ���
�����ƂȂ�ƁA��L�́i�ؖ��j�̂悤�ȕ��@�ɂȂ�܂��B
�i�NjL�j�@�ߘa�U�N�W���R���t��
�@���k��w�@�������ʁi�P�X�V�U�j�ŁA���̖�肪�o�肳�ꂽ�B�f�p�ɐ����v�Z����Ή�����
���������B�ŏ��A�n�~���g���E�P�[���[�̒藝���g�����Ƃ������A��肭�����Ȃ������B
��R���@�@�s��
�@�@ 
������ �`2�|���`���`-1 �����Ƃ��A�`3 �����߂�B�������A�����|�������P �Ƃ���B
�i���j
�@ �@�A
�@�A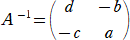
�Ȃ̂ŁA�@��2�{�����|���������@���Ȃ킿�A�@������2�|�P�@�E�E�E�@�i�P�j
�@�i���{���j���|�������|���@���Ȃ킿�A�@�i���{�P�j�����O�@�E�E�E�@�i�Q�j
�@�i���{���j���|�������|���@���Ȃ킿�A�@�i���{�P�j�����O�@�E�E�E�@�i�R�j
�@�����{��2�|��2�����@���Ȃ킿�A�@���������@�E�E�E�@�i�S�j
�@���{�P���O�@�̂Ƃ��A�i�Q�j�i�R�j���A�@���������O�@�ŁA�i�S�j���A�@�����O
���̂Ƃ��A�@�����|�������O�@�ƂȂ�A�����|�������P �ɖ�������B
�@����āA�����|�P�@�ŁA�i�P�j���A�@�����O�@�A�������|�P
�n�~���g���E�P�C���C�̒藝���A�@�o2�|�i���{���j�o�{�d���O�@�i�d�͒P�ʍs��j
���Ȃ킿�A�@�o2�{�o�{�d���O�@�Ȃ̂ŁA�@�o3�|�d���i�o�|�d�j�i�o2�{�o�{�d�j���O
����āA�@�o3���d�@�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�W���Q�W���t��
�@���̓��k��w�@���n�i�P�X�V�X�j�̖��́A�s��̐��������肷����ł���B�n�~���g���E
�P�[���[�̒藝������ł������Ȗ��ł���B
����@�@�s��
�@�@ 
������ �`3���d �����悤�Ɏ��� ���A���A�� ���߂�B�������A�d�͒P�ʍs��Ƃ���B
�i���j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{���j�`�{�i�����|��2�j�d���O
���Ȃ킿�A�@�`3�|�i���{���j�`2�{�i�����|��2�j�`���O�@����A
�@�d�|�i���{���j�i�i���{���j�`�|�i�����|��2�j�d�j�{�i�����|��2�j�`���O
����āA�@�i�i���{���j2�|�i�����|��2�j�j�`���i�i���{���j�i�����|��2�j�{�P�j�d
�i���{���j2�|�i�����|��2�j���O�@�̂Ƃ��A�@�`�����d�@�i���͎����j�@�Ə�����B
���Ȃ킿�A�@�`3����3�d���d�@���A�@��3���P�@�������āA�@�����P
�@���̂Ƃ��A�@�����P�@�A�����O�@�A�����P
�@����́A�i���{���j2�|�i�����|��2�j���O�@�����B
�i���{���j2�|�i�����|��2�j���O�@�̂Ƃ��A�@�i���{���j�i�����|��2�j���|�P
���Ȃ킿�A�@�i���{���j3���|�P�@����A�@���{�����|�P�@�A�@�����|��2���P
�����ŁA�����|���|�P�@�ŁA��2���|��2�|���|�P���O�@�ƂȂ�A���̎������������͑��݂��Ȃ��B
�ȏォ��A�@�����P�@�A�����O�@�A�����P�@�ł���B�@�@�i�I�j
�i�R�����g�j�@���u�Б�w�i�Q�O�O�X�j�ŁA�ޑ肪�o�肳��Ă���B
�@�d���Q���̒P�ʍs��Ƃ��āA�Q���̐����s��
�@�@ 
�� �`2���d ���݂����Ƃ���B�������A���A���A���͎����ł���A�����O �Ƃ���B
���̂Ƃ��A�� �̒l����蓾��͈͂����߂�B
�܂��A�� �̒l�����͈̔͂ɂ���Ƃ��A�� ����� �� �� �� �ŕ\���B
�i���j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{���j�`�{�i�����|��2�j�d���O
���Ȃ킿�A�@�i���{���j�`���i�����|��2�{�P�j�d
���{�����O�@�̂Ƃ��A�`�����d�@�i���͎����j�@�Ə����邪�A�����O ����s�K
����āA�@���{�����O�@�A�����|��2���|�P
�����|���@�������āA��2���P�|��2���O�@����A�|�P�������P�@�ŁA�@������i�P�|��2�j�@�@�i�I�j
�@���̓��k��w�@���n�i�P�X�W�O�j�̖��ɂ����Ă��A�n�~���g���E�P�[���[�̒藝������B
���T�@�@�s��
�@�@
�ŕ\�����P���ϊ��́A�������b �F ������2�|�� ��̓_���˂ɂb��̓_�ɂ����Ƃ���B
�i�P�j�@�� �� �� �� �� ��p���ĕ\���B
�i�Q�j�@����ɁA�`2�|�U�`�{�W�d���n�@�ł���Ƃ��A�s��`�����߂�B
�������A�d�͒P�ʍs��ŁA�n�͗�s��ł���B
�i���j�i�P�j�@������2�|�� ��̓_�i���C��2�|���j�́A�P���ϊ��`�ɂ��A
�@�i����2�{�i���|���j���C����2�{�i���|���j���j
�ɂ�����A���ꂪ�܂��b��̓_�Ȃ̂ŁA
�@����2�{�i���|���j�����i����2�{�i���|���j���j2�|�i����2�{�i���|���j���j
����A��2���O�@�A�Q���i���|���j���O�@�A�i���|���j2�|�������@�A�|�i���|���j�����|���@�Ȃ̂ŁA
�@�����O�@�A������2�@�A�������|������2�|��
�i�Q�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i��2�{���j�`�{��3�d���n
�@�`2�|�U�`�{�W�d���n�@�Ȃ̂ŁA�@�i��2�{���|�U�j�`���i��3�|�W�j�d
��2�{���|�U���O�@�̂Ƃ��A�@�`�����d�@�Ƃ�����B���Ȃ킿�A��2�|�U���{�W���O�@����A�����Q�A�S
�@����āA�`���Q�d�@�A�S�d
��2�{���|�U���O�@�̂Ƃ��A�@�i���{�R�j�i���|�Q�j���O�@����A�@�����|�R�A�Q
�@�����|�R�@�̂Ƃ��A�����O�A�����P�Q�A�����X
�@�����Q�@�̂Ƃ��A�����O�A�����Q�A�����S�@�@�i�I�j
�@���̓��k��w�@���n�i�P�X�W�O�j�̖��́A�P���ϊ��Ɋւ�����ł���B
����@�@�@�s��
�@
�ŕ\�����P���ϊ��́A���ʏ�̓_(�P�C�Q)�A(�Q�C�P)�����ꂼ��_ (�T�C�O)�A(�S�C�R)�ɂ�����
����B
�i�P�j�@�s��`�����߂�B
�i�Q�j�@���̂P���ϊ��ɂ���āA���_�𒆐S�Ƃ��锼�a�P�̉~�͂ǂ̂悤�Ȑ}�`�ɂ�����邩�B
�i���j�i�P�j�@�������A�@���{�Q�����T�A�Q���{�����S�@����A�����P�A�����Q
�@���{�Q�����O�A�Q���{�����R�@����A�����Q�A�����|�P
�@����āA
�@�@
�i�Q�j�@�s��`�����āA
�@�@
�@�����A�P���ϊ��`�ɂ��A���_�𒆐S�Ƃ��锼�a�P�̉~�� �� ���Ɋւ��đΏ̈ړ����A����ɁA
��]�ړ������A������ �̑����g�傳�������̂����߂�}�`�ł���B
�̑����g�傳�������̂����߂�}�`�ł���B
�@���������āA���߂�}�`�́A���_�𒆐S�Ƃ��锼�a �̉~�ł���B�@�@�i�I�j
�̉~�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�X���Q�R���t��
�@���̓��k��w�@���n�i�P�X�W�P�j�̖����A�o���l���K�v�Ȗ��ł���B
���T
�@�@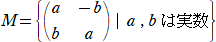
�Ƃ���B
�i�P�j�@�n�łȂ�M�̍s��A�ɑ��āAAX���n ����M�̍s��w�����߂�B�������A�n�͗�s
�@��ł���B
�i�Q�j
�@�@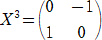
�@�����l�̍s��w�����߂�B
�i���j�i�P�j
�@�@�@�@
�ɂ����āA�������`����2�{��2 �ƂȂ�B�s��A�́A�n�łȂ��̂ŁA���A�� �̉��ꂩ�͂O�łȂ��B
����āA�@�������`����2�{��2���O �ƂȂ�̂ŁA�`�̋t�s��`-1�����݂���B
�ȏォ��A�@�w���`-1�n���n�@�ł���B
�i�Q�j
�@�@
�Ƃ����ƁA��ӂ��A�����v�Z�����āA�@���i��2�|�R��2�j���O�@�A���i�R��2�|��2�j���P
�@�����O�@�̂Ƃ��A�@�|��3���P�@����A�@�����|�P
�@��2���R��2�@�̂Ƃ��A�@�W��3���P�@����A�@�����P/�Q�@�ŁA�@�����} /�Q
/�Q
���������āA���߂�w�́A
�@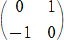 �@�A
�@�A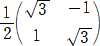 �@�A
�@�A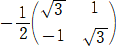 �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���Q���t��
�@���̓��k��w�@���n�i�P�X�W�P�j�ł́A�P���ϊ��I�戵���ł���B
����@�@�n�����_�Ƃ��镽�ʂ̂P���ϊ��e�������āA�C�ӂ̓_�o���������_���p�Ƃ���Ƃ��A
�@�@����OQ�̒����͐���OP�̒����̂Q�{�ɂȂ��Ă���B�Ƃ��ɂe�͓_(�P�C�O)��_( �C�|�P)��
�C�|�P)��
�@�@�����B���̂悤�ȂP���ϊ��e��\���s��A�����߂�B
�i���j�@���߂�s��`��
�@�@
�Ƃ����ƁA��ӂ��A�@���� �@�A�����|�P
�@�A�����|�P
�܂��A�@�i�����{�����j2�{�i�����{�����j2���S�i��2�{��2�j�@���A�@��2�{��2���S�@�A ���|�����O
���|�����O
�����������āA�@�����}�P�@�A�����} �@�i���������j�@�@�i�I�j
�@�i���������j�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���U���t��
�@���̓��k��w�@�������ʁi�P�X�W�Q�j�̖��́A�悭����ꂽ�ǖ₾�Ǝv���B
���P�@�@�s��
�@�@ �@�@�i���A���A���A�� �͎����j
�@�@�i���A���A���A�� �͎����j
�́A�`2���` �����B
�i�P�j�@�������P/�S �̂Ƃ��A�� �� �� �̒l�����߂�B
�i�Q�j�@����ɁA�O�����{���{���{�����Q �Ƃ��āA�s��`�����߂�B
�i���j�i�P�j�@��ӂ��A�@��2�{���������@�A�i���{���j�������@�A�i���{���j�������@�A�����{��2����
�@�������P/�S �Ȃ̂ŁA�@�����O�@�A�����O�@���A�@���{�����P
�@�����P�|���@���A�����{��2�����@�ɑ�����Đ�������ƁA�@a2�|���{�������O
�����ŁA���ʎ����c�Ƃ����ƁA�� �͎����Ȃ̂ŁA�@�c���P�|�S�������O�@���A�@�������P/�S
�@�������P/�S �Ȃ̂ŁA�@�������P/�S�@���A�@a2�|���{�P/�S���O�@����āA�@�����P/�Q�@�A�����P/�Q
�i�Q�j�@���{�����P�@���A�@�|�P�����{�����P�@�ł���B�����ŁA���{�������@�Ƃ����ƁA���A�� �́A
�@�Q�������� ��2�|�����{�P/�S���O�@�̂Q�̎������ł���B
����āA���ʎ����c�Ƃ����ƁA�@�c����2�|�P���O�@���A�@�����|�P�@�A�����P
�@�|�P�������P�@���A�@�����|�P�@�ƂȂ�B�@��2�{���{�P/�S���O�@�������āA���������|�P/�Q
�ȏォ��A
�@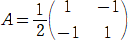 �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���P�S���t��
�@���̓��k��w�@���n�i�P�X�W�Q�j�̖��́A�ŗL�l�̌v�Z�𗍂߂����ł���B
���T�@�@�s��
�@�@
�ɂ��āA���̖�ɓ�����B
�i�P�j�@�`�������@�������i���C���j�@�� ��2�{��2���P �Ƃ��ɖ������_P(x�Cy) (x���O)������B�� ��
�@�@�_�o�̍��W�� �� �ŕ\���B
�i�Q�j�@�i�P�j�̂Ƃ��A����ɁA�`�w�����w�@�i�����P�j�@�w�����i�w�C�x�j�@�� �w2�{�x2���P �Ƃ��ɖ���
�@�@���_�p(�w�C�x) (�x���O) �����݂���悤�� �� �� �� �ŕ\���A�_�p�̍��W�� �� �ŕ\���B
�i�R�j�@���_���n�Ƃ���Ƃ��A���n�o�p�̖ʐς����߂�B
�i���j�i�P�j�@�������A�@�Q�����{���������@�A�����{���������@���A
�@�i�Q���|�P�j���{�������O�@�A�����{�i���|�P�j�����O
�i���C���j���i�O�C�O�j�@�Ȃ̂ŁA�i�Q���|�P�j�i���|�P�j�|��2���O�@�����A�@������o�i�P�|�Q���j�i�P�|���j�p
���̂Ƃ��A�@�����i�P�|�Q���j/���E������o�i�P�|�Q���j/�i�P�|���j�p�E���@���A
�@��2�{�o�i�P�|�Q���j/�i�P�|���j�p�E��2���P�@�Ȃ̂ŁA�@��2���i�P�|���j/�i�Q�|�R���j
����āA�@������o�i�P�|���j/�i�Q�|�R���j�p�@�A������o�i�P�|�Q���j/�i�Q�|�R���j�p�@���A
�@�o�i��o�i�P�|���j/�i�Q�|�R���j�p�C��o�i�P�|�Q���j/�i�Q�|�R���j�p�j
�i�Q�j�@�������A�@�Q���w�{���x�����w�@�A���w�{���x�����x�@���A
�@�i�Q���|���j�w�{���x���O�@�A���w�{�i���|���j�x���O
�i�w�C�x�j���i�O�C�O�j�@�Ȃ̂ŁA�i�Q���|���j�i���|���j�|��2���O�@�����A
�@�i�Q���|���j�i���|���j�|�i�Q���|�P�j�i���|�P�j���O�@���A�@�i���|�P�j�i���|�R���{�P�j���O
����āA�����P�@�Ȃ̂ŁA�@�����R���|�P
���̂Ƃ��A�@�i�P�|���j�w�{���x���O�@�A���w�{�i�P�|�Q���j�x���O
�@�w���|�o�i�P�|�Q���j/���p�x���|��o�i�P�|�Q���j/�i�P�|���j�p�E�x�@���A
�@�i�P�|�Q���j/�i�P�|���j�E�x2�{�x2���P�@�Ȃ̂ŁA�@�x2���i�P�|���j/�i�Q�|�R���j�@���A
�@�x����o�i�P�|���j/�i�Q�|�R���j�p�@����āA�@�w���|��o�i�P�|�Q���j/�i�Q�|�R���j�p
���������āA�p�i�|��o�i�P�|�Q���j/�i�Q�|�R���j�p�C��o�i�P�|���j/�i�Q�|�R���j�p�j
�i�R�j�@�n�o�E�n�p���O�@���A�@�n�o�ۂn�p
����āA���n�o�p���i�P/�Q�j�E�P�E�P���P/�Q�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���Q�O���t��
�@���̓��k��w�@���n�i�P�X�W�R�j�̖��́A�ŗL�x�N�g���Ɋւ�����ł���B
���T�@�@�s��
�@�@ �@
�@
�́A�C�ӂ̃x�N�g���@�������i�� ���j�@�ɑ��āA�@�`���E�������E�����i�P/�S�j�`���E�`���@�����B
�i�P�j�@�`�����߂�B
�i�Q�j�@�����O�@�̂Ƃ��A�� �� �`�� �̂Ȃ��p�����߂�B
�i�R�j�@�`�̒�߂�P���ϊ��ɂ���āA�~�� �o�i���C���j�b��2�{��2���P�A�����O�A�����O�p�͂ǂ̂悤��
�@�@�}�`�ɂ�����邩�B�}�ɂ���Ď����B
�i���j�i�P�j�@�������A
�@�`���E��������2�{�i���{���j�����{����2����2�{��2���i�P/�S�j�i�i�����{�����j2�{�i�����{�����j2�j
����A�����P�A�����P�A���{�����O�A��2�{��2���S���A�����{�������O�A��2�{��2���S��
����āA�@��2���R�A��2���R�@�ŁA���{�����O�@����A�@�i���C���j���i �C�|
�C�| �j�A�i�|
�j�A�i�| �C
�C �j
�j
���������āA���߂�s��`�́A
�@�@ �@�A
�@�A
�i�Q�j�@�� �� �`�� �̂Ȃ��p���ƂƂ����ƁA�b�`���b���Q�b���b�@�Ȃ̂ŁA
�@�������Ɓ��`���E��/�i�b�`���b�b���b�j���b���b2/�i�Q�b���b2�j���P/�Q�@���A�@�Ɓ���/�R
�i�R�j�@�P���ϊ��`�́A
�@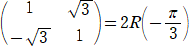
����A���_���S�Ɂ|��/�R��]�����āA�Q�{�Ɋg�傳����悢�B
�@
����A���_���S�Ƀ�/�R��]�����āA�Q�{�Ɋg�傳����悢�B
�@�ȏォ��A�`�̒�߂�P���ϊ��ɂ���āA�~�� �o�i���C���j�b��2�{��2���P�A�����O�A�����O�p�̂���
�����}�`�́A���}�̐����������ɂȂ�B
�@�@ �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�O���Q�W���t��
�@���̓��k��w�@�������ʁi�P�X�W�S�j�̖��́A�މ����b��̖��ł���B
���P�@�@���ʏ�ŁA�s��
�@�@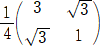
�ɂ��^������P���ϊ����e�A���_�̂܂��Ɂ|��/�R��]����P���ϊ����f�Ƃ���B
�i�P�j�@���ʏ�̔C�ӂ̓_���e�ɂ���āA���钼���k��̓_�ɂ�����邱�Ƃ������A�k�̕���
�@�@�������߂�B
�i�Q�j�@�o(���C��)���k��̓_�Ƃ���B�����ʑ��e�f�ɂ���āA�o�ɂ������_�S�̂̂���}�`
�@�@�����߂�B
�i���j�i�P�j�@�e�F�i���C���j���i�w�C�x�j�@�Ƃ���ƁA�@�w���i�R���{ ���j/�S�@�A�x���i
���j/�S�@�A�x���i ���{���j/�S�@����A
���{���j/�S�@����A
�@�w�� �x�@�ƂȂ�̂ŁA���߂钼���k�̕������́A�@����
�x�@�ƂȂ�̂ŁA���߂钼���k�̕������́A�@���� ��
��
�i�Q�j�@�o(���C��)���k��̓_�Ƃ���ƁA�@���� ���@�����藧�B���̂Ƃ��A
���@�����藧�B���̂Ƃ��A
�@�e�f�F�i���C���j���i�i /�Q�j���C�i�P/�Q�j���j��(���C��)�@����A�@�����Q���@�A�� �͔C��
/�Q�j���C�i�P/�Q�j���j��(���C��)�@����A�@�����Q���@�A�� �͔C��
����āA���߂�}�`�̕������́A�@�����Q���@�ŁA����́A�_�i�O�C�Q���j��ʂ�A�� ���ɕ��s�Ȓ�
���ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�P���Q�O���t��
�@���̓��k��w�@���n�i�P�X�W�U�j�̖����A�މ����b��̖��ł���B
���R�@�@�i�P�j�@�s��
�@�@
�ɂ��āA�`3���` ����������悤�� ���A�� ���߂�B
�i�Q�j�@�i�P�j�� ���A�� �ɑ��āA�P���ϊ� ���f�������{�����@�A���f�����{�����@���l����B���̂P���ϊ�
�@�ɂ��~ ��2�{��2���P �̑���}������B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�Q���`�{�i��2�|���j�d���O�@�i�d�͒P�ʍs��j
���Ȃ킿�A�@�`2���Q���`�|�i��2�|���j�d�@���A
�@�`3���Q���`2�|�i��2�|���j�`���i�R��2�{���j�`�|�Q���i��2�|���j�d���`
����āA�@�i�R��2�{���|�P�j�`���Q���i��2�|���j�d
�`���j�d�@���A�@�R��2�{���|�P���O�@�A���i��2�|���j���O
�����O�@���A�@��2�����@�Ȃ̂ŁA�@��2���P/�S�@���Ȃ킿�A�@�����P/�Q�@�A�����P/�S
�i�Q�j�@���f���i�P/�Q�j���{�i�P/�S�j���@�A���f�����{�i�P/�Q�j���@����A�@���f���Q���f
����āA��2�{��2���P ��̓_�́A���� �����Q�� ��ɂ������B
�������A�@�����������ƁA�����������Ɓ@�Ƃ����ƁA
�@���f���i�P/�Q�j�������Ɓ{�i�P/�S�j�������Ɓ��i /�S�j�������i�Ɓ{���j�@�i�������A�����������Q�j�@���A
/�S�j�������i�Ɓ{���j�@�i�������A�����������Q�j�@���A
�@�| /�S�����f��
/�S�����f�� /�S
/�S
�ȏォ��A�~ ��2�{��2���P �̑��́A���� �����Q���@�i�| /�S������
/�S������ /�S�j�@�ł���B�@�@�i�I�j
/�S�j�@�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�P���Q�T���t��
�@���̓��k��w�@���n�i�P�X�W�U�j�̖��́A���n�i�P�X�W�U�j�̖��̗ޑ�ł���B
����@�@�s��
�@�@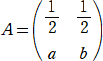
�ɂ��āA�`3���` �����藧�悤�� ���A�� ���߂�.
�i���j�@�n�~���g���E�P�[���[�̒藝���A
�@�`2�|�i���{�P/�Q�j�`�{�i�P/�Q�j�i���|���j�d���O�@�i�d�͒P�ʍs��j
�`3���` �Ȃ̂ŁA
�@�`�|�i���{�P/�Q�j�i�i���{�P/�Q�j�`�|�i�P/�Q�j�i���|���j�d�j�{�i�P/�Q�j�i���|���j�`���O
���Ȃ킿�A�@�i�i���{�P/�Q�j2�|�i�P/�Q�j�i���|���j�|�P�j�`���i�P/�Q�j�i���{�P/�Q�j�i���|���j�d
�@�`�����d�@�Ȃ̂ŁA�@�i���{�P/�Q�j2�|�i�P/�Q�j�i���|���j�|�P���O�@�A�i���{�P/�Q�j�i���|���j���O
�������@�̂Ƃ��A�@�i���{�P/�Q�j2���P�@����A�@���������P/�Q�@�A�|�R/�Q
�����|�P/�Q�@�̂Ƃ��A�@���|�����|�Q�@����A�@�����R/�Q�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�P���Q�V���t��
�@���̓��k��w�@���n�i�P�X�W�V�j�̖��́A���w�ɂ͂Ȃ��p�^�[���ŁA��������B
���P�@�@�s��
�@�@
�ɑ��A���� ���A���A�Ɓi�|��/�Q���Ɓ���/�Q�j�@�����݂���
�@�@
�ƕ\���邱�Ƃ������B����ɁA���̂Ƃ��� ���A�� �� ���A���A�� �ŕ\���B
�i���j�@��2�{��2����2�@�ŁA�����O�@����A�@�i��/���j2�{�P���i��/���j2
�����ŁA�@��/�����������Ӂ@�A��/�����P/�������Ӂ@�i�|��/�Q���Ӂ���/�Q�j�@�Ƃ����ƁA
�@�������E�������Ӂ@�A�������E��������
�����ŁA
�@�@
����A�@�Ӂ|�Ɓ���/�Q�{�Ɓ@���Ȃ킿�A�@�Ɓ���/�S�|��/�Q�@�Ƃ����ƁA
�@�|��/�Q���Ӂ���/�Q�@����A�@�|��/�Q���O���Ɓ���/�Q�@�ŁA
�@�������E�������Ɓ@�A�����|���E�������Ɓ@�Ƃ����ƁA
�@
�����藧�B���̂Ƃ��A
�@�������E�������i��/�Q�{�Q�Ɓj���|���E�������Q�Ɓ��|�Q���E�������Ƃ������Ɓ��Q����/��
�@�������E�������i��/�Q�{�Q�Ɓj�����E�������Q�Ɓ����i������2�Ɓ|������2�Ɓj���i��2�|��2�j/��
���A�@��2�|��2�������@�A����������/�Q
�@�i��2�{��2�j2���i��2�|��2�j2�{�S��2��2����2��2�{��2��2���i��2�{��2�j��2����4
����āA�@��2�{��2����2�@����A�@��2���i�����{��2�j/�Q�@���A�@������2�Ɓ��i���{���j/�i�Q���j
�@�|��/�Q���O���Ɓ���/�Q�@�ɂ����āA�������Ɓ��O�@�Ȃ̂ŁA�@�������Ɓ���o�i���{���j/�i�Q���j�p
����āA�@��������o�i���{���j/�i�Q���j�p
�܂��A
�@�@
����A�@���������Ɓ|���������Ɓ����������Ɓ@���A�@�������Ɓ��i���|���j/��
��2�{��2����2�@����A��2����2�|��2���i���|���j�i���{���j�@�Ȃ̂ŁA�@�������Ɓ��|��/�i���{���j
����āA�������Ɓ��������ƁE�������Ɓ��|��/�i���{���j�E��o�i���{���j/�i�Q���j�p�@���A
�@�������E��/�i���{���j�E��o�i���{���j/�i�Q���j�p������o��/�i�Q�i���{���j�j�p�@�@�i�I�j
�i�NjL�j�@�ߘa�U�N�P�Q���T���t��
�@���̓��k��w�@���n�i�P�X�W�V�j�̖��́A�P���ϊ��Ɩʐς̊W��₤�Ă���B
����@�@���A�� �������Ƃ���B
�i�P�j�@�s��
�@�@
�ŕ\�����1���ϊ��e�́A���� ���ʂ̌��_�n���P�̒��_�Ƃ���C�ӂ́��n�o�p������Ɩʐς�
���������n�o�f�p�f�ɂ����B���A�� �̖������ׂ����������߂�B
�i�Q�j�@�i�P�j�̏����̂��ƂŁA�e�ɂ���ē_(�Q�C�|�P)�ɂ������_�� �� ���W���ő�ɂȂ�Ƃ�
�@�� ���A�� �̒l�����߂�B
�i�R�j�@�i�Q�j�̏����̂��ƂŁA�_�d1(�P�C�O)�A�d2(�P�C�P)�A�d3(�O�C�P)�ɑ��āA�����`�n�d1�d2�d3�́A
�@�e�ɂ���āA�ǂ̂悤�Ȑ}�`�ɂ��邩�B�}������B
�i���j�i�P�j�@1���ϊ��e�ɂ���āA�ʐς́A�b�������`�b���b��2�{��2�b����2�{��2�@�{�ɂȂ�̂ŁA
�Ή�����O�p�`�̖ʐς����������Ƃ���A��2�{��2���P�@�ł���B
�i�Q�j�@�_�i���C���j���A�e�ɂ���ē_(�Q�C�|�P)�ɂ������Ƃ��A�@�����Q���|���@�����藧�B
�@���� �����Q���|�� ���A�~ ��2�{��2���P �ɐڂ���Ƃ��A�@�b���b/ ���P�@���A�@�����}
���P�@���A�@�����}
����āA���� �̂Ƃ��A�ő�ƂȂ�̂ŁA�����Q���|
�̂Ƃ��A�ő�ƂȂ�̂ŁA�����Q���| �@�� ��2�{��2���P�@�ɑ�����āA
�@�� ��2�{��2���P�@�ɑ�����āA
�@�T��2�|�S ���{�S���O�@���Ȃ킿�A�@�i
���{�S���O�@���Ȃ킿�A�@�i ���|�Q�j2���O�@���A�@�����Q/
���|�Q�j2���O�@���A�@�����Q/ �A�����|�P/
�A�����|�P/
�i�R�j�@�e�F�d1 �� �i�Q/ �C�|�P/
�C�|�P/ �j�@�A�e�F�d2 �� �i�R/
�j�@�A�e�F�d2 �� �i�R/ �C�P/
�C�P/ �j�@�A�e�F�d3 �� �i�P/
�j�@�A�e�F�d3 �� �i�P/ �C�Q/
�C�Q/ �j
�j
�@����āA�e�ɂ�鐳���`�n�d1�d2�d3�̑��́A���}�ƂȂ�B
�@�@ �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P���W���t��
�@���̓��k��w�@���n�i�P�X�W�W�j�̖����A�P���ϊ��ɊW������ł���B
����@�@�i�P�j�@�s��
�@�@
�ŕ\�����P���ϊ����A�Ȑ� �������P ��̂��ׂĂ̓_���Ȑ� ��2�|��2���Q ��̓_�ɂ�����
���A�`�͂ǂ̂悤�ȍs�B�s��`�̊e������ �� �̎��Ƃ��ĕ\���B
�i�Q�j�@����ɁA���̂P���ϊ��̋t�ϊ����A�Ȑ� �������P ��̂��ׂĂ̓_���Ȑ� ��2�|��2���Q ��
�@�̓_�ɂ����Ƃ��A�`�����߂�B
�i���j�i�P�j�@�`�F�i���C�P/���j�@���@�i�����{��/���C�����{��/���j�@�Ƃ���ƁA
�@�i�����{��/���j2�|�i�����{��/���j2���Q�@���A
�@�i��2�|��2�j��2�{�i��2�|��2�j�i�P/��2�j�{�Q�i�����|�����|�P�j���O
�@��2�|��2���O�@�A��2�|��2���O�@�A�����|�������P
����āA�@�����}���@�A�����}���@�i�����C�Ӂj
�����|�������P�@�Ȃ̂ŁA�@�������@�A�����|���@�܂��́A�@�����|���@�A������
���̂Ƃ��A����ɂ��Ă��A�@�������P/�Q�@���A�@�����P/�i�Q���j
�ȏォ��A
| �@ |
 |
�@�܂��́A |
 |
�i�Q�j
| �@ |
 |
�@�̂Ƃ��A |
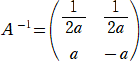 |
�`-1�F�i���C�P/���j�@���@�i��/�i�Q���j�{�P/�i�Q�����j�C�����|��/���j�@���A
�@�i��/�i�Q���j�{�P/�i�Q�����j�j2�|�i�����|��/���j2���Q�@���A
�@�i�P/�i�S��2�j�|��2�j��2�{�i�P/�i�S��2�j�|��2�j�i�P/��2�j�{�P/�i�Q��2�j�{�Q��2���Q
�@�P/�i�S��2�j����2�@�A�P/�i�S��2�j�{��2���P�@���A�@�Q��2���P�@�A����āA�����}�P/
���������āA
| �@ |
 |
�@�܂��́A |
 |
�܂��A
�@�@
�̂Ƃ��A�������P��̓_�i�P�C�P�j�́A�`�ɂ��A�i���{�P/�i�Q���j�C�|���|�P/�i�Q���j�j�Ɉڂ���邪�A
�@�i���{�P/�i�Q���j�j2�|�i�|���|�P/�i�Q���j�j2���O�@���A��2�|��2���Q ��ɂȂ��_�ł���B
�@����āA���̏ꍇ�͕s�K�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P���P�P���t��
�@���̓��k��w�@���n�i�P�X�W�X�j�̖����A�P���ϊ��ɊW������ł���B
���Q�@�@�s��
�@�@ �@�@�i�O���Ɓ���/�Q�j
�@�@�i�O���Ɓ���/�Q�j
�̕\���P���ϊ����e�Ƃ���B�~C�F(���|�Q)2�{��2���S/�R �̂e�ɂ�鑜���b1�Ƃ���B
�i�P�j�@�Ȑ��b1�͉~�ł��邱�Ƃ������A���̒��S�̍��W�Ɣ��a�����߂�B
�i�Q�j�@�Q�~�b�Ƃb1���O�ڂ���悤�ɃƂ��߂�B
�i���j�i�P�j�@�������`��������4�Ɓ{������2�Ƃ�����2�Ɓ�������2�Ɓi������2�Ɓ{������2�Ɓj��������2�Ɓ��O
���A
�@�@
�Ȑ��b1��̓_�i���C���j�ɑ��āA�`-1�ɂ�鑜�́A�i���{���������ƁC�|���������Ɓ{���j
���ꂪ�b��̓_�Ȃ̂ŁA�i���{���������Ɓ|�Q�j2�{�i�|���������Ɓ{���j2���S/�R
���Ȃ킿�A�i�P�{������2�Ɓj��2�{�i�P�{������2�Ɓj��2�|�S���|�S���������Ɓ{�W/�R���O�@���A
�@��2�{��2�|�i�S/�i�P�{������2�Ɓj�j���|�i�S��������/�i�P�{������2�Ɓj�j���{�i�W/�R�j/�i�P�{������2�Ɓj���O
�P�{������2�Ɓ��P/������2�Ɓ@�Ȃ̂ŁA
�@��2�{��2�|�S������2�ƁE���|�S�������Ƃ������ƁE���{�i�W/�R�j������2�Ɓ��O
����āA
�i���|�Q������2�Ɓj2�{�i���|�Q�������Ƃ������Ɓj2
���|�i�W/�R�j������2�Ɓ{�S������4�Ɓ{�S������2�Ƃ�����2�Ɓ��i�S/�R�j������2��
�ȏォ��A�Ȑ��b1�͉~�ł��邱�Ƃ�������A���S�̍��W�́A�i�Q������2�ƁC�Q�������Ƃ������Ɓj
���a�́A�i�Q/ �j�������Ɓ@�ł���B
�j�������Ɓ@�ł���B
�i�Q�j�@�Q�~�b�Ƃb1���O�ڂ��邽�߂ɂ́A
�i�Q������2�Ɓ|�Q�j2�{�i�Q�������Ƃ������Ɓj2���i�i�Q/ �j�{�i�Q/
�j�{�i�Q/ �j�������Ɓj2���i�S/�R�j�i�P�{�������Ɓj2
�j�������Ɓj2���i�S/�R�j�i�P�{�������Ɓj2
���Ȃ킿�A�@�S������4�Ɓ|�W������2�Ɓ{�S�{�S������2�Ƃ�����2�Ɓ��i�S/�R�j�i������2�Ɓ{�Q�������Ɓ{�P�j
���A
�@�i�P�U/�R�j������2�Ɓ{�i�W/�R�j�������Ɓ|�i�W/�R�j���O
����āA�@�Q������2�Ɓ{�������Ɓ|�P���i�Q�������Ɓ|�P�j�i�������Ɓ{�P�j���O�@���A�������Ɓ��P/�Q�A�|�P
�O���Ɓ���/�Q�@���A�@�Ɓ���/�R�@�@�i�I�j
�i�R�����g�j�@������4�Ɓ{������2�Ƃ�����2�Ɓ�������2�Ɓ@�Ƃ������ό`���ڗ����܂����I�����ƁA�o��
�@�@�@�@�҂̕��̂��C�ɓ���Ȃ�ł��傤�ˁD�D�D�B
�i�NjL�j�@�ߘa�V�N�R���P�R���t��
�@���̓��k��w�@�O�����n�i�P�X�X�O�j�̖��́A�n�~���g���E�P�[���[�̒藝�ɊW������
�ł���B
����@�@���A���A���A�� �͎����Ƃ��āA�s��
�@�@
�ɂ��āA���̖�ɓ�����B
�i�P�j�@�`�����d�@�i���͎����j�@�ŁA���� ���A�� ������ �`2�|���`�{���d���n�@�����Ƃ��A���A�� ��
�@���A���A���A�� �ŕ\���B�����ŁA�d�͒P�ʍs��A�n�͗�s���\�����̂Ƃ���B
�i�Q�j�@A�� �`���n�AA3�{A���n �����AA�͋t�s��������AA-1���|�` �ƂȂ邱�Ƃ������B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{���j�`�{�i�����|�����j�d���n
����āA�@�i���|�i���{���j�j�`���i���|�i�����|�����j�j�d
�@�`�����d�@�i���͎����j�@�Ȃ̂ŁA�@�������{���@�A���������|����
�i�Q�j�@�������`���O�@�Ƃ���ƁA�@�`2���i���{���j�`�@���A�@�i���{���j�`2���|�`�@���Ȃ킿�A
�@�i���{���j2�`���|�`�@�@�������A�`���n �Ȃ̂ŁA�@�i���{���j2���|�P
�@���A�� �͎����Ȃ̂ŁA����͖����B�@���������āA�������`���O�@�ŁAA�͋t�s������B
���̂Ƃ��AA3���|A�@����AA2���|�d�@���A�`���|�`-1�@�����A�@A-1���|�` �ƂȂ�B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�R���P�T���t��
�@���̓��k��w�@�O�����n�i�P�X�X�O�j�̖��́A�u�L���v�Ƃ��������̎g������Ⴢ�܂��ˁI
����@�@�������A���i�i���C���j���i�O�C�O�j�j�ɑ��āA
�@�@
�Œ�߂���s����l����B
�i�P�j�@���ʏ���O�łȂ��x�N�g���Ƃ���Ƃ��A�x�N�g���̑傫���̔�b�`���b/�b���b�����A��
�@�@���g���ĕ\���B
�i�Q�j�@�s��̏W���o�`���b�����O�C�P�C�Q�C�E�E�E�p���L���W���ƂȂ�Ƃ��A�`�͉�]�̍s��ł��邱
�@�@�Ƃ������B�������A�`0�͒P�ʍs��d��\�����̂Ƃ���B
�i�R�j�@�o�`���b�����O�C�P�C�Q�C�E�E�E�p���Q�̗v�f���琬��悤�ɂ��A�����߂�B
�i���j�i�P�j�@�������i���C���j�@�Ƃ����ƁA�@�`�������i�����|�����C�����{�����j�@�ł���B���̂Ƃ��A
�@�b�`���b2���i�����|�����j2�{�i�����{�����j2���i��2�{��2�j�i��2�{��2�j
�����ŁA�@�b���b2����2�{��2�@�Ȃ̂ŁA�@�b�`���b2���i��2�{��2�j�b���b2
����āA�@�b�`���b/�b���b����i��2�{��2�j
�i�Q�j�@��i��2�{��2�j�����@�i�����O�j�@�Ƃ����B�@��/�����������Ɓ@�A��/�����������Ɓ@�ƂȂ�Ƃ��߂�ƁA
�@�`�����E�q�i�Ɓj�@�i�q�i�Ɓj�͉�]�p�Ƃ̉�]�s��j
�@�s��̏W���o�`���b�����O�C�P�C�Q�C�E�E�E�p���L���W���Ƃ������Ƃ���A
�@�`�����`0 �ƂȂ邎�����݂���B
���̂Ƃ��A�����E���������Ɓ��P�A�����E���������Ɓ��O�@����A�@�������P�@�����A�����P
���������āA�`���q�i�Ɓj�@�ƂȂ�A��]�p�Ƃ̉�]�s��ƂȂ�B
�i�R�j�@��ӂ��A�@�o�`���b�����O�C�P�C�Q�C�E�E�E�p���o�d�C�`�p�@�ƂȂ�B
���������āA�@�`2���d�@�܂��́@�`2���`
�@�����ŁA�`2���`�@�Ƃ���ƁA�@�`���d�@�ƂȂ�A��ӂɔ�����B
����āA�@�`2���d�@�ł���B���Ȃ킿�A�@�������Q�Ɓ��P�@�A�������Q�Ɓ��O
�@��������Ƃ́A�Ɓ��O�A��
�`���d�@�Ȃ̂ŁA�@�Ɓ��O�@�͕s�K
�ȏォ��A�Ɓ��@�ŁA�@�`���|�d�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�R���P�W���t��
�@���̓��k��w�@������n�i�P�X�X�O�j�̖��́A�P���ϊ��Ɋւ�����ł���B
����@�@���A�� �͎����ŁA�����O �Ƃ���B�s��
�@�@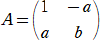
�ɂ��\�����1���ϊ�
�@�@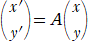
�ɂ��čl����B
�i�P�j�@A2�{A�{E��O �����悤�ɂ`���߂�B�����ŁA�d�͒P�ʍs��A�n�͗�s���\����
�@�@�̂Ƃ���B
�i�Q�j�@���_���n(�O�C�O)�A���� �����Q ��̓_��P(�Q�C��)�Ƃ��A�i�P�j�Œ�߂�ꂽ�s��`�ɂ��P��
�@�@�ϊ��ŁA�_�o���_�p�Ɉڂ���̂Ƃ���B�b�n�p�b���b�n�o�b�ƂȂ�悤�Ȃ��͈̔͂����߂�B
�i�R�j�@�i�Q�j�̑傫���̔�b�n�p�b/�b�n�o�b�̍ő�l�����߂�B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{�P�j�`�{�i��2�{���j�d���n
�@A2���|A�|E ���A�@�i���{�Q�j�`���i��2�{���|�P�j�d
�@�`�����d�@�i���͎����j�@�Ȃ̂ŁA�@���{�Q���O�@�A��2�{���|�P���O�@���A�@�����|�Q�@�A����
�i�Q�j�@�`�F�i�Q�C���j�@���@�i�Q�| ���C�Q
���C�Q �|�Q���j�@�Ȃ̂ŁA
�|�Q���j�@�Ȃ̂ŁA
�@�i�Q�| ���j2�{�i�Q
���j2�{�i�Q �|�Q���j2���S�{��2�@���Ȃ킿�A�@��2�|�Q
�|�Q���j2���S�{��2�@���Ȃ킿�A�@��2�|�Q ���{�Q���O
���{�Q���O
����������āA�@���� �|�P�@�A
�|�P�@�A �{�P����
�{�P����
�i�R�j�@�i�Q�| ���j2�{�i�Q
���j2�{�i�Q �|�Q���j2�����i�S�{��2�j�@�i�����O�j�@�Ƃ����ƁA
�|�Q���j2�����i�S�{��2�j�@�i�����O�j�@�Ƃ����ƁA
�@�i���|�V�j��2�{�P�Q ���{�S���|�P�U���O
���{�S���|�P�U���O
���̂Q���������������������悤�ɂ��̒l�͈̔͂����߂�悢�B
�@�����V�@�̂Ƃ��A�����|�P/ �@�Ƃ�������������A���߂邋�͈̔͂Ɋ܂܂��B
�@�Ƃ�������������A���߂邋�͈̔͂Ɋ܂܂��B
�@�����V�@�̂Ƃ��A���ʎ����c�Ƃ����ƁA�������������߂ɂ́A
�@�c/�S���P�O�W�|�i���|�V�j�i�S���|�P�U�j���|�S��2�{�S�S���|�S���O�@�����A�@��2�|�P�P���{�P���O
����������āA�@�O���i�P�P�|�R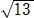 �j/�Q�������V�A�V�������i�P�P�{�R
�j/�Q�������V�A�V�������i�P�P�{�R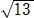 �j/�Q
�j/�Q
�����V�@���܂߂āA�@�i�P�P�|�R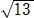 �j/�Q�������i�P�P�{�R
�j/�Q�������i�P�P�{�R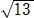 �j/�Q
�j/�Q
���������āA�る�̍ő�l�́A�@��i�i�P�P�{�R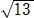 �j/�Q�j���i
�j/�Q�j���i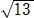 �{�R�j/�Q�@�@�i�I�j
�{�R�j/�Q�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�R���Q�T���t��
�@���̓��k��w�@������n�i�P�X�X�O�j�̖����A�P���ϊ��Ɋւ�����ł���B
����@�@�}�`C�F�V��2�{�R��2�|�S �������X �ɂ��āA���̖�ɓ�����B
�������X �ɂ��āA���̖�ɓ�����B
�i�P�j�@�}�`C�����_�̂܂��ɂR�O��������]�����}�`�̕����������߂�B
�i�Q�j�@�}�`C���~ ��2�{��2���P �Ɉڂ��P���ϊ���\���s��
�@�@ �@�@�i���A���A���A�� �͎����A�����|�������O�j
�@�@�i���A���A���A�� �͎����A�����|�������O�j
�@�ŁA�_�i �C�P�j��_(�P�C�P/
�C�P�j��_(�P�C�P/ )�Ɉڂ����̂����߂�B
)�Ɉڂ����̂����߂�B
�i���j�i�P�j�@�_�i���C���j�����_�̂܂��ɂR�O��������]�����_���i�w�C�x�j�Ƃ���ƁA
�@�����i �w�{�x�j/�Q�@�A�����i�|�w�{
�w�{�x�j/�Q�@�A�����i�|�w�{ �x�j/�Q
�x�j/�Q
����� �V��2�{�R��2�|�S �������X �ɑ�����Đ�������ƁA�@�X�w2�{�x2���X
�������X �ɑ�����Đ�������ƁA�@�X�w2�{�x2���X
���Ȃ킿�A�@��2�{��2/�X���P
�i�Q�j�@���������̂P/�R�k���̂P���ϊ����a�Ƃ���ƁA�P���ϊ��a�q�i�R�O���j�ɂ��A�Ȑ��b�́A
�@�~ ��2�{��2���P �Ɉڂ����B����āA���߂�P���ϊ��́A
�@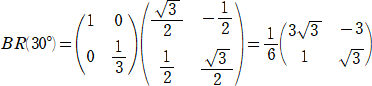
���̂P���ϊ��ɂ��A�_�i �C�P�j�͓_(�P�C�P/
�C�P�j�͓_(�P�C�P/ )�Ɉڂ���邩��A���������B�@�@�i�I�j
)�Ɉڂ���邩��A���������B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�R���R�O���t��
�@���̓��k��w�@�O�����n�i�P�X�X�P�j�̖��́A�����������̉�@���܂�ł���B
����@�@�e�i���j�A�f�i���j�͔����\�Ȋ��Ƃ��A�s��
�@�@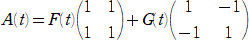
�͂��ׂĂ̎��� ���A�� �ɑ��āA���̂Q�̏��������Ƃ���B
�i�P�j�@A(���{��)��A(��)A(��)
�i�Q�j�@A(t)�̕\���P���ϊ��͑o�Ȑ�C�Fx2�|y2���P ��̔C�ӂ̓_��C��Ɉڂ��B
���̂Ƃ��A�e�i���j�A�f�i���j�͂ǂ̂悤�Ȋ����B
�i���j�@A(���{��)��A(��)A(��)�@�̐����v�Z���āA
�@�e�i���{���j�{�f�i���{���j���Q�i�e�i���j�e�i���j�{�f�i���j�f�i���j
�@�e�i���{���j�|�f�i���{���j���Q�i�e�i���j�e�i���j�|�f�i���j�f�i���j
������A�@�e�i���{���j���Q�e�i���j�e�i���j�@�A�f�i���{���j���Q�f�i���j�f�i���j
�܂��AA(t)�ɂ��A�b��̓_�i�P�C�O�j�́A�i�e�i���j�{�f�i���j�C�e�i���j�|�f�i���j�j�Ɉڂ���A���̓_���܂�
�b��ɂ���̂ŁA�@�i�e�i���j�{�f�i���j�j2�|�i�e�i���j�|�f�i���j�j2���P�@���Ȃ킿�A�@�e�i���j�f�i���j���P/�S
�@����āA�@�e�i���j���O�@�A�f�i���j���O�@�ƂȂ�B
�@�e�i���{���j���Q�e�i���j�e�i���j�@�ŁA���������O�@�Ƃ����ƁA�@�e�i�O�j���Q�e�i�O�j2
�@�e�i�O�j���O�@�Ȃ̂ŁA�@�e�i�O�j���P/�Q�@���l�ɂ��āA�@�f�i�O�j���P/�Q
�@�e�i���{���j���Q�e�i���j�e�i���j�@�̗��ӂ� �� �Ɋւ��Ĕ�������ƁA�@�e�f�i���{���j���Q�e�f�i���j�e�i���j
�@�����O�@�Ƃ����ƁA�@�e�f�i���j���Q�e�f�i�O�j�e�i���j
�@�����ŁA�@�Q�e�f�i�O�j�����@�Ƃ����ƁA���͒萔�ŁA�@�e�f�i���j�����e�i���j
�@�e�f�i���j/�e�i���j�����@����A�@�������b�e�i���j�b�������{�b�@���A�@�e�i���j���}��^�i�����{�b�j
�@�}��^�b���c�@�Ƃ����ƁA�@�e�i���j���c��^�i�����j�@�i�c�͒萔�j
�@�����ŁA�@�e�i�O�j���c���P/�Q�@���A�@�e�i���j���i�P/�Q�j��^�i�����j
�@�e�i���j�f�i���j���P/�S�@���A�@�f�i���j���i�P/�Q�j��^�i�|�����j
�@�t�ɁA�e�i���j���i�P/�Q�j��^�i�����j�A�f�i���j���i�P/�Q�j��^�i�|�����j�@�̂Ƃ��A���̏��������B�i�I�j
�i�NjL�j�@�ߘa�V�N�S���R���t��
�@���̓��k��w�@�O�����n�i�P�X�X�P�j�̖��́A���n�ɂ��ޑ肪�o�肳��Ă���B
����@�@�� �������Ƃ��A�_(�P�C�|�P)��_( �C�|
�C�| )�ɁA�_(�P�C�P)��_(�Q���|
)�ɁA�_(�P�C�P)��_(�Q���| �C�Q
�C�Q �|�Q��)
�|�Q��)
�@�@�Ɉڂ��P���ϊ����e�Ƃ���B����ɁA�����k�F ���{�����P ��̓_�on (�����P�A�Q�A�R�A�E�E�E)����
�@�@�̂悤�ɋA�[�I�ɒ�߂�B
�i�@�j�@�_(�P/�Q�C�P/�Q�j���o1�Ƃ���B
�i�A�j�@�on���e�ňڂ����_���o�fn�Ƃ��A���_�n�Ƃo�fn��ʂ钼�����k�ƌ����_���on+1�Ƃ���B
�@���̂Ƃ��A
�i�P�j�@�b�on�on+1�b�� �� �� �� �ŕ\���B
�i�Q�j�@�b�o1�o8�b���U�R�T/ �ƂȂ�悤�� �� �̒l�����߂�B
�ƂȂ�悤�� �� �̒l�����߂�B
�i���j�i�P�j�@�P���ϊ��e��\���s��e�́A
�@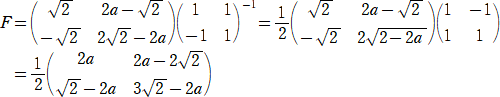
�܂��A
�@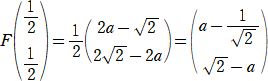
���A�o�f1�i���|�P/ �C
�C �|���j�@�ł���B���̂Ƃ��A�����n�o�f1�̕������́A
�|���j�@�ł���B���̂Ƃ��A�����n�o�f1�̕������́A
�@�����i �|���j/�i���|�P/
�|���j/�i���|�P/ �j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�o2�́A
�j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�o2�́A
�@�i �|���j/�i���|�P/
�|���j/�i���|�P/ �j�E�����P�|���@���A�@����
�j�E�����P�|���@���A�@���� ���|�P
���|�P
����āA�@�o2�i ���|�P�C�Q�|
���|�P�C�Q�| ���j
���j
�@��ʂɁA�on�i�����C�P�|�����j�ɑ��āA�o�fn�i���f���C���f���j�Ƃ����ƁA
�@���f�����������{�i���| �j�i�P�|�����j�����|
�j�i�P�|�����j�����| �{
�{ ����
����
�@���f�����i�P/ �|���j�����{�i�i�R/�Q�j
�|���j�����{�i�i�R/�Q�j �|���j�i�P�|�����j���i�R/�Q�j
�|���j�i�P�|�����j���i�R/�Q�j �|���|
�|���| ����
����
���̂Ƃ��A�����n�o�fn�̕������́A
�@�����i�i�R/�Q�j �|���|
�|���| �����j/�i���|
�����j/�i���| �{
�{ �����j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�on+1�́A
�����j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�on+1�́A
�@�i�i�R/�Q�j �|���|
�|���| �����j/�i���|
�����j/�i���| �{
�{ �����j�E�����P�|���@���A�@����
�����j�E�����P�|���@���A�@���� ���|�Q�{�Q����
���|�Q�{�Q����
����āA�@��n+1���Q�����{ ���|�Q�@���A�@��n+1�{
���|�Q�@���A�@��n+1�{ ���|�Q���Q�i�����{
���|�Q���Q�i�����{ ���|�Q�j�@�Ȃ̂ŁA
���|�Q�j�@�Ȃ̂ŁA
�@�����{ ���|�Q���Qn-1�i��1�{
���|�Q���Qn-1�i��1�{ ���|�Q�j���Qn-1�i
���|�Q�j���Qn-1�i ���|�R/�Q�j�@���A
���|�R/�Q�j�@���A
�@�������Qn-1�i ���|�R/�Q�j�{�Q�|
���|�R/�Q�j�{�Q�| ��
��
����āA�@�������P�|�������|�Qn-1�i ���|�R/�Q�j�|�P�{
���|�R/�Q�j�|�P�{ ��
��
�܂��A�@����+1���Qn�i ���|�R/�Q�j�{�Q�|
���|�R/�Q�j�{�Q�| �� �A����+1���|�Qn�i
�� �A����+1���|�Qn�i ���|�R/�Q�j�|�P�{
���|�R/�Q�j�|�P�{ ��
��
�ȏォ��A
�b�on�on+1�b2���i�Qn-1�i ���|�R/�Q�j�j2�{�i�Qn-1�i
���|�R/�Q�j�j2�{�i�Qn-1�i ���|�R/�Q�j�j2
���|�R/�Q�j�j2
�@���Q�E�i�Qn-1�i ���|�R/�Q�j�j2
���|�R/�Q�j�j2
���Ȃ킿�A�@�b�on�on+1�b�� �E�Qn-1�b
�E�Qn-1�b ���|�R/�Q�b���Qn-1�b�Q���|�R/
���|�R/�Q�b���Qn-1�b�Q���|�R/ �b
�b
�i�Q�j�@�b�o1�o8�b���i�P�{�Q�{�E�E�E�{�U�S�j�b�Q���|�R/ �b���P�Q�V�b�Q���|�R/
�b���P�Q�V�b�Q���|�R/ �b���U�R�T/
�b���U�R�T/
����āA�@�b�Q���|�R/ �b���T/
�b���T/ �@�������āA�@�����Q
�@�������āA�@�����Q �@�A�|�P/
�@�A�|�P/ �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�S���V���t��
�@���̓��k��w�@�O�����n�i�P�X�X�P�j�̖��́A��L�̗��n�̗ޑ�ł���B
����@�@�_(�P�C�|�P)��_( �C�|
�C�| )�ɁA�_(�P�C�P)��_(
)�ɁA�_(�P�C�P)��_( �C�O)�Ɉڂ��P���ϊ����e�Ƃ���B
�C�O)�Ɉڂ��P���ϊ����e�Ƃ���B
�@�@����ɁA�����k�F ���{�����P ��̓_�on (�����P�A�Q�A�R�A�E�E�E)�����̂悤�ɋA�[�I�ɒ�߂�B
�i�@�j�@�_(�P/�Q�C�P/�Q�j���o1�Ƃ���B
�i�A�j�@�on���e�ňڂ����_���o�fn�Ƃ��A���_�n�Ƃo�fn��ʂ钼�����k�ƌ����_���on+1�Ƃ���B
�@���̂Ƃ��A��n���b�on�on+1�b�Ƃ���ƁA����o��n�p�͂ǂ̂悤�Ȑ��B
�i���j�i�P�j�@�P���ϊ��e��\���s��e�́A
�@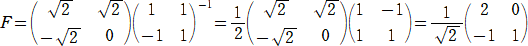
�܂��A�on�i�����C�����j�ɑ��āA�o�fn�i���f���C���f���j�Ƃ����ƁA
�@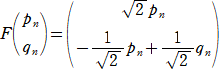
���A�@���f���� �����@�A���f�����|�i�P/
�����@�A���f�����|�i�P/ �j�����{�i�P/
�j�����{�i�P/ �j����
�j����
���̂Ƃ��A�����n�o�fn�̕������́A
�@�����i�|�i�P/ �j�����{�i�P/
�j�����{�i�P/ �j�����j/�i
�j�����j/�i �����j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�on+1�́A
�����j�E���@�Ȃ̂ŁA�����k�Ƃ̌�_�on+1�́A
�@�i�|�i�P/ �j�����{�i�P/
�j�����{�i�P/ �j�����j/�i
�j�����j/�i �����j�E�����P�|���@���A�@�����Q����
�����j�E�����P�|���@���A�@�����Q����
����āA�@��n+1���Q�����@�Ə�����B
�@��1���P/�Q�@���A���ׂĂ̎��R�����ɑ��āA�������O �ł���B
�@�on�i�����C�P�|�����j�ɑ��āA�on+1�i�Q�����C�P�|�Q�����j �ƂȂ�̂ŁA
��n2���b�on�on+1�b2������2�{����2���Q����2�@���A�@��n�� ����
����
���̂Ƃ��A�@��n+1�� ����+1���Q
����+1���Q �������Q��n ����A
�������Q��n ����A
�@����o��n�p�́A����  ��1���P/
��1���P/ �ŁA����Q�̓��䐔��ł���B�@�@�i�I�j
�ŁA����Q�̓��䐔��ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�S���P�P���t��
�@���̓��k��w�@������n�i�P�X�X�P�j�̖��́A�u���Ɋւ�����ł���B
����@�@�P���ϊ��e��\���s��e���@�e3���d�A�e���d�@�i�d�͒P�ʍs��j�@�����Ă���B�܂��A
�@�@���قȂ�R�_�`(�P�C�O)�A�a(�O�C�Q)�A�b(���C��)�̂e�ɂ�鑜�e�i�`�j�A�e�i�a�j�A�e�i�b�j�͂��ꂼ��`�A
�@�@�a�A�b�̂����ꂩ�Ɉ�v���Ă���Ƃ���B
�i�P�j�@�e�i�`�j�A�e�i�a�j�A�e�i�b�j�͑��قȂ邱�Ƃ������B
�i�Q�j�@�e�i�`�j���`�A�e�i�a�j���a�A�e�i�b�j���b �ł��邱�Ƃ������B
�i�R�j�@���A�� ����� �e �����߂�B
�i���j�i�P�j�@�e�i�`�j���e�i�a�j�@�Ɖ��肷��ƁA�e3�i�`�j���e3�i�a�j ���Ȃ킿�A�@�`���a�@�ƂȂ�A�s�K�B
�@����āA�e�i�`�j���e�i�a�j�@�ł���B���l�ɁA�e�i�a�j���e�i�b�j�A�e�i�b�j���e�i�`�j�@�ł���B
���������āA�@�e�i�`�j�A�e�i�a�j�A�e�i�b�j�͑��قȂ�B
�i�Q�j�@�e�i�`�j���`�A�e�i�a�j���a�A�e�i�b�j���b ��ے肷��ƁA
�@�e�i�`�j���`�@�܂��́@�e�i�a�j���a�@�܂��́@�e�i�b�j���b
�E�e�i�`�j���`�@�A�e�i�a�j���a�@�A�e�i�b�j���b �̂Ƃ��A�@�e���d�@�ƂȂ�A�s�K
�E�e�i�`�j���`�@�A�e�i�a�j���a�@�A�e�i�b�j���b �̂����Q�����藧�Ƃ��A�@�e���d�@�ƂȂ�A�s�K
�E�e�i�`�j���`�@�A�e�i�a�j���a�@�A�e�i�b�j���b �̂����P���������藧�Ƃ��A
�@���Ƃ��A�e�i�`�j���`�@�̂Ƃ��A�e�i�a�j���b�@�A�e�i�b�j���a �ƂȂ�̂ŁA
�@�e3�i�a�j���e2�i�b�j���e�i�a�j���b�@�ƂȂ�A�e3���d�@�ł��邱�Ƃɔ�����B�������l�B
���������āA�e�i�`�j���`�A�e�i�a�j���a�A�e�i�b�j���b �ł���B
�i�R�j�@�i�P�j�i�Q�j���A
�@�e�i�`�j���a�@�A�e�i�a�j���b�@�A�e�i�b�j���`�@�܂��́A�e�i�`�j���b�@�A�e�i�a�j���`�@�A�e�i�b�j���a
��P�̏ꍇ�A
�@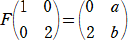 �@�@ �@�@ |
����A |
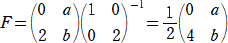 |
�@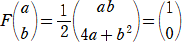
���A�@�������Q�@�A�S���{��2���O�@�������āA�@�����|�P�@�A�����|�Q
���̂Ƃ��A
�@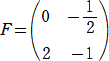
��Q�̏ꍇ�A
�@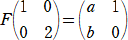 �@ �@ |
����A |
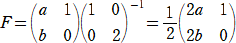 |
�@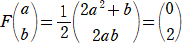
���A�@�Q��2�{�����O�@�A�������Q�@�@�������āA�@�����|�P�@�A�����|�Q
���̂Ƃ��A
�@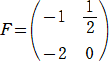 �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�S���P�R���t��
�@���̓��k��w�@������n�i�P�X�X�P�j�̖��́A���w�I�A�[�@��p������ł���B
����@�@���� �� �ɑ��A�`�i���j�����Œ�`����B
�@�@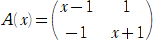
�i�P�j�@�`�i���j�`�i���j���`�i�����j�{�i���{���|�P�j�`�i�O�j�@���ؖ�����B
�i�Q�j�@�����Q�ȏ�̐����̂Ƃ��A�@�`�i���jn���`�i��n�j�{�i����n-1�|�P�j�`�i�O�j �����藧���Ƃ��ؖ�
�@�@����B�������A�`�i���j1���`�i���j�A�`�i���jn���`�i���j�`�i���jn-1 �i�����Q�j �Ƃ���B
�i���j�i�P�j�@��`���A
�@�@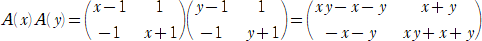
�@�@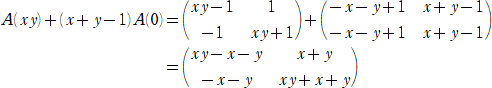
�Ȃ̂ŁA�@�`�i���j�`�i���j���`�i�����j�{�i���{���|�P�j�`�i�O�j�@�����藧�B
�i�Q�j�@�i�P�j�ŁA�������@�Ƃ����ƁA�@�`�i���j2���`�i��2�j�{�i�Q���|�P�j�`�i�O�j �����藧�̂ŁA�����
�@�����Q�̂Ƃ����藧�B
�@�������i�����Q�j�@�̂Ƃ��A���肪���藧�Ɖ��肷��B���Ȃ킿�A
�@�`�i���j�����`�i�����j�{�i������-1�|�P�j�`�i�O�j
���̂Ƃ��A
�@�`�i���j��+1���`�i���j�`�i���jk���`�i���j�i�`�i�����j�{�i������-1�|�P�j�`�i�O�j�j
���`�i���j�`�i�����j�{�i������-1�|�P�j�`�i���j�`�i�O�j
���`�i����+1�j�{�i���{�����|�P�j�`�i�O�j�{�i������-1�|�P�j�i�`�i�O�j�{�i���|�P�j�`�i�O�j�j
���`�i����+1�j�{�i�i���{�P�j�����|�P�j�`�i�O�j
�Ȃ̂ŁA����́A�������{�P�̂Ƃ������藧�B
���������āA�����Q�ȏ�̐����̂Ƃ��A
�@�`�i���jn���`�i��n�j�{�i����n-1�|�P�j�`�i�O�j �����藧�B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�S���P�W���t��
�@���̓��k��w�@�O���������ʁi�P�X�X�Q�j�̖��́A�P�Ȃ鐬���v�Z�ł���B
����@�@�s��
�@�@ �@�A
�@�A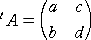
�@�ɂ��āA���̖�ɓ�����B
�i�P�j�@���� At�`�����`�` �����藧�Ƃ��A�`�̐����̊Ԃɂ͂ǂ̂悤�ȊW�����邩�B
�i�Q�j�@�����R/�T �̂Ƃ��AAt�`�����`�`���d�@�i�d�͒P�ʍs��j �����s��`�����ׂċ��߂�B
�i���j�i�P�j�@�����v�Z�ɂ��A��2�{��2����2�{��2�@�A�����{�����������{�����@�A��2�{��2����2�{��2
���Ȃ킿�A�@��2����2�@�A�i���|���j�i���|���j���O
��2����2�@���A�i���|���j�i���{���j���O�@�Ȃ̂ŁA�@�������@�܂��́A�@�����|��
�@�������@�̂Ƃ��A�@���A�� �͔C�ӂ̐�
�@�����|���@�ŁA�����O�@�̂Ƃ��́A�������@�̂Ƃ��ƈ�v����̂ŁA�����O�@�Ƃ��Ă悢�B
�@���̂Ƃ��A�@�������@�ƂȂ�B
�i�Q�j�@�����v�Z�ɂ��A
�@��2�{��2����2�{��2���P�@�A�����{�����������{�������O�@�A��2�{��2����2�{��2���P
�����R/�T �̂Ƃ��A��2���P�|�X/�Q�T���P�U/�Q�T�@����A�����}�S/�T
�@��2���P�|�X/�Q�T���P�U/�Q�T�@����A�����}�S/�T
�@�����}�S/�T�@���A��2���P�|�P�U/�Q�T���X/�Q�T�@����A�����}�R/�T
�i�P�j���A�@���������S/�T�@�̂Ƃ��A���{�����O�@�ɒ��ӂ��āA�����R/�T�A�����|�R/�T
�@���������|�S/�T�@�̂Ƃ��A���{�����O�@�ɒ��ӂ��āA�����R/�T�A�����|�R/�T
�@�����S/�T�A�����|�S/�T�@�̂Ƃ��A�@�����R/�T�A�����R/�T
�@�����|�S/�T�A�����S/�T�@�̂Ƃ��A�@�����R/�T�A�����R/�T�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���R���t��
�@���̓��k��w�@������n�i�P�X�X�Q�j�̖��́A�P���ϊ��̌v�Z�ł���B
����@�@�s��
�@�@
�ŕ\�����P���ϊ��e�ɂ���āA�~ x2�{y2���P ���~ x2�{y2���Q �ɕϊ�����A�o�Ȑ� �������P
���o�Ȑ� ��2�|��2���S �ɕϊ������Ƃ��A���̍s������߂�B
�i���j�@��ӂ��A�P���ϊ��e�́A������ �̌��_���S�A��]�p�Ƃ̉�]�ړ�
�̌��_���S�A��]�p�Ƃ̉�]�ړ�
�@�@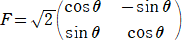
���A�܂��́A������ �̒��� �������i�������Ɓj�Ɋւ���Ώ̈ړ�
�̒��� �������i�������Ɓj�Ɋւ���Ώ̈ړ�
�@�@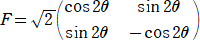
�̉��ꂩ�ł���B
�@�@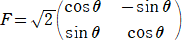
�̂Ƃ��A�@�e-1�F�i���C���j���i�w�C�x�j�@�Ƃ���ƁA
�@�w���i���������Ɓ{���������Ɓj/ �@�A�x���i�|���������Ɓ{���������Ɓj/
�@�A�x���i�|���������Ɓ{���������Ɓj/
�w�x���P�@�Ȃ̂ŁA�@�i���������Ɓ{���������Ɓj�i�|���������Ɓ{���������Ɓj���Q
���Ȃ킿�A�@�|��2�������Q�Ɓ{�Q�����������Q�Ɓ{��2�������Q�Ɓ��S
��2�|��2���S �Ȃ̂ŁA�@�������Q�Ɓ��|�P�@�A�������Q�Ɓ��O
�O���Ɓ��Q�@���A�@�Q�Ɓ��R��/�Q�@�A�V��/�Q�@�Ȃ̂ŁA�@�Ɓ��R��/�S�@�A�V��/�S
����āA
�@ �@�A
�@�A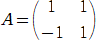
�@�@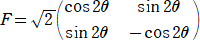
�̂Ƃ��A�@�e-1�F�i���C���j���i�w�C�x�j�@�Ƃ���ƁA
�@�w���i���������Q�Ɓ{���������Q�Ɓj/ �@�A�x���i���������Q�Ɓ|���������Q�Ɓj/
�@�A�x���i���������Q�Ɓ|���������Q�Ɓj/
�w�x���P�@�Ȃ̂ŁA�@�i���������Q�Ɓ{���������Q�Ɓj�i���������Q�Ɓ|���������Q�Ɓj���Q
���Ȃ킿�A�@��2�������S�Ɓ|�Q�����������S�Ɓ|��2�������S�Ɓ��S
��2�|��2���S �Ȃ̂ŁA�@�������S�Ɓ��P�@�A�������S�Ɓ��O
�O���Q�Ɓ��S�@���A�@�Q�Ɓ���/�S�@�A�T��/�S�@�Ȃ̂ŁA�@�Ɓ���/�W�@�A�T��/�W
����āA
�@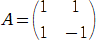 �@�A
�@�A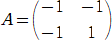 �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���U���t��
�@���̓��k��w�@�O�����n�i�P�X�X�R�j�̖��́A�P�Ȃ鐬���v�Z�ł���B
����@�@�s��
�@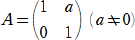
�ŁA�d�͒P�ʍs��Ƃ��A�m���`���|�d�@�i���͎��R���j�@�ɂ��āA���̖�ɓ�����B
�i�P�j�@�m2�A�i�d�{�m�j�i�d�|�m�j �����߂�B
�i�Q�j�@�d�|�m���t�s��������Ƃ������A�i�d�|�m�j-1 �����߂�B
�i�R�j�@���� �w2���m �����s�� �w �͑��݂��Ȃ����Ƃ��ؖ�����B
�i���j�i�P�j�@���w�I�A�[�@�ɂ��A
�@�@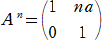
�Ȃ̂ŁA
�@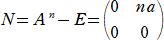
���̂Ƃ��A
�@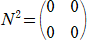
����ɁA�@�i�d�{�m�j�i�d�|�m�j���d�@�ł���B
�i�Q�j�@�i�d�{�m�j�i�d�|�m�j���d�@�Ȃ̂ŁA�d�|�m�͋t�s��������A�@�i�d�|�m�j-1���d�{�m���`��
�i�R�j�@���� �w2���m �����s�� �w �����݂���Ɖ��肷��B
�@�@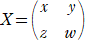
�Ƃ����ƁA�@��2�{�������O�@�A�i���{���j���������@�A�i���{���j�����O�@�A�����{��2���O
���͎��R���ŁA�����O�@����A�@�i���{���j�����O�@���A�@���{�����O�@�A�����O
�i���{���j�����O�@���A�@�����O�@�ƂȂ�A�@��2���O�@�A��2���O�@���Ȃ킿�A�@���������O
����āA���{�����O�@�ƂȂ�A���{�����O�@�Ɩ�������B
���������āA���� �w2���m �����s�� �w �͑��݂��Ȃ��B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���P�O���t��
�@���̓��k��w�@�O�����n�i�P�X�X�R�j�̖����A�P�Ȃ鐬���v�Z�ł���B
����@�@���_���n�Ƃ��A�s��
�@�@
�ɂ���ĕ\�����P���ϊ����e�Ƃ���B�R�_�o1(�P�C�O)�A�o2�i�P/ �C�P/
�C�P/ �j�A�o3�i�O�C�P�j�̂e��
�j�A�o3�i�O�C�P�j�̂e��
��鑜�����ꂼ��o1�f�A�o2�f�A�o3�f�Ƃ����B���ς̒l�ɂ��āA
�@�n�o1�E�n�o1�f���P�A�n�o2�E�n�o2�f���R�A�n�o3�E�n�o3�f���R �ł���Ƃ��A���̖�ɓ�����B
�i�P�j�@���A���A�� �����߂�B
�i�Q�j�@�_�o(�������ƁC�������Ɓj�̂e�ɂ�鑜���o�f�Ƃ���B�Ƃ� �O���Ɓ��� �͈̔͂ŕω�����Ƃ��A
�@�@�n�o�E�n�o�f�̍ő�l�ƍŏ��l�A����т����̒l��^����Ƃ̒l�����߂�B
�i���j�i�P�j�@�o1�f�i���C���j�@���A�n�o1�E�n�o1�f�������P
�@�o2�f�i�i���{���j/ �C�i���{���j/
�C�i���{���j/ �j�@���A�n�o2�E�n�o2�f���i���{���j/�Q�{�i���{���j/�Q���R
�j�@���A�n�o2�E�n�o2�f���i���{���j/�Q�{�i���{���j/�Q���R
����āA�@���{�Q���{�����U�@����A�Q���{�����T
�@�o3�f�i���C���j�@���A�n�o3�E�n�o3�f�������R�@�Ȃ̂ŁA�@�����P
�i�Q�j�@�o�f�i�������Ɓ{�������ƁC�������Ɓ{�R�������Ɓj�@���A
�@�n�o�E�n�o�f��������2�Ɓ{�Q�������Ƃ������Ɓ{�R������2�Ɓ��������Q�Ɓ{�P�{�Q������2��
�@���������Q�Ɓ|�������Q�Ɓ{�Q�� �������i�Q�Ɓ|��/�S�j�{�Q
�������i�Q�Ɓ|��/�S�j�{�Q
�@�O���Ɓ��� ���A�@�|��/�S���Q�Ɓ|��/�S���R��/�S�@�Ȃ̂ŁA
�n�o�E�n�o�f�́A�Q�Ɓ|��/�S����/�Q�@�����A�Ɓ��R��/�W�@�̂Ƃ��A�ő�ŁA�ő�l�@ �{�Q
�{�Q
�@�Q�Ɓ|��/�S���R��/�Q�@�����A�Ɓ��V��/�W�@�̂Ƃ��A�ŏ��ŁA�ŏ��l�@�| �{�Q�@�@�i�I�j
�{�Q�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���P�Q���t��
�@���̓��k��w�@�O�����n�i�P�X�X�R�j�̖����A�P�Ȃ鐬���v�Z�ł���B
����@�@�Q�̗�x�N�g���t�����i�Q�C�P�j�A�u�����i�P�C�R�j�ƁA���������ׂĎ����ł���s��
�@�@
�ɂ��āA�`2�t���u�@�A�`2�u���t�@�������ɂ͐������Ȃ����Ƃ��ؖ�����B
�i���j�@�`2�t���u�@�A�`2�u���t�@�������ɐ���������̂Ɖ��肷��B
�@�`2�i�t�C�u�j���i�u�C�t�j�@����A
�@�@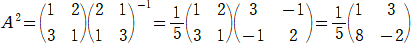
�܂��A
�@�@
�Ȃ̂ŁA�@��2�{�������P/�T�@�A�����{�������R/�T�@�A�����{�������W/�T�@�A�����{��2���|�Q/�T
��P���Ƒ�S������A�@��2�|��2���R/�T
��Q���ƘA�����āA�@�i���{���j�i���|���j���i���{���j���@�ŁA���{�����O�@����A�@���|������
����āA�@���{�����R/�i�T���j�@�ƂȂ�B���̂Ƃ��A��R�����A�@�����W��/�R
�������S���ɑ�����āA�@�W��2/�R�{��2���|�Q/�T
�@���ӂ͂O�ȏ�ł���̂ɑ��āA�E�ӂ͂O��菬�����B����͖����ł���B
�@����āA�`2�t���u�@�A�`2�u���t�@�͓����ɂ͐������Ȃ��B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���P�R���t��
�@���̓��k��w�@�O�����n�i�P�X�X�R�j�̖��́A��]�ړ��̖��ł���B
����@�@�`�A���A�� �𐳂̐��Ƃ���B�Ȑ�
�@�i���{���j�i��2�{��2�j�{�Q�i���|���j�����|�Q�`�i���{���j�{�Q��2���O�@�E�E�E�@�i*�j
�� �� ���� �� ���Ƃɐڂ���Ƃ��A���̖�ɓ�����B
�i�P�j�@�`�� ���A�� �ŕ\���A�Ȑ��i*�j�� �� ���ɐڂ���_�A����сA�� ���ɐڂ���_�̍��W������
�@���ꋁ�߂�B
�i�Q�j�@�Ȑ��i*�j�����_�̂܂��ɂS�T����]�����ē�����Ȑ��̕����������߁A�Ȑ��i*�j��
�@�ȉ~�ł��邱�Ƃ��m���߂�B
�i���j�i�P�j�@�����O�@�Ƃ��āA�@�i���{���j��2�|�Q�`���{�Q��2���O
�@���ʎ����c�Ƃ��āA�@�c/�S���`2�|�Q��2�i���{���j���O�@����A�@�`������i�Q�i���{���j�j���O
���̂Ƃ��A�� ���ɐڂ���_�́A�@�i�`/�i���{���j�C�O�j���i ��/��i���{���j�C�O�j
��/��i���{���j�C�O�j
�@�����O�@�Ƃ��āA�@�i���{���j��2�|�Q�`���{�Q��2���O
���̂Ƃ��A�� ���ɐڂ���_�́A�@�i�O�C�`/�i���{���j�j���i�O�C ��/��i���{���j�j
��/��i���{���j�j
�i�Q�j�@�q�i�S�T���j�F�i���C���j�@���@�i�w�C�x�j�@�Ƃ���ƁA�q�i�|�S�T���j�F�i�w�C�x�j�@���@�i���C���j
���̂Ƃ��A�@�����i�w�{�x�j/ �A�����i�|�w�{�x�j/
�A�����i�|�w�{�x�j/ �@�Ȃ̂ŁA
�@�Ȃ̂ŁA
�@�i���{���j�i�w2�{�x2�j�{�i���|���j�i�|�w2�{�x2�j�|�Q�`�E �x�{�Q��2���O�@����A
�x�{�Q��2���O�@����A
�@���w2�{���x2�|�Q����i���{���j�x�{��2���O
����āA�Ȑ��i*�j�����_�̂܂��ɂS�T����]�����ē�����Ȑ��̕������́A
�@����2�{����2�|�Q����i���{���j���{��2���O
�ł���B����2�{���i���|��i���{���j�j2�������@����A��2/���{�i���|��i���{���j�j2/�����P�@�ƂȂ�̂ŁA
����́A�ȉ~�̕������ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���P�V���t��
�@���̓��k��w�@������n�i�P�X�X�R�j�̖��́A�P�Ȃ鐬���v�Z�ł���B
����@�@�s��
�@�@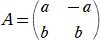
�ɂ���Ē�܂�P���ϊ����e�Ƃ����A���_�n�ƈقȂ�Q�_�o1�i��1�C��1�j�A�o2�i��2�C��2�j�̂e�ɂ��
�����o1�f�A�o2�f�ƕ\���B�n�o1���n�o2�A�n�o1�f���n�o2�f�����ꂼ��A�݂��ɒ�������Ƃ��A��
�̖�ɓ�����B�������A��1���O�A��1���O�A���������O �Ƃ���B
�i�P�j�@�n�o1�� �� ���̂Ȃ��p�Ɓi�O���Ɓ���/�Q�j�����߂�B
�i�Q�j�@�n�𒆐S�Ƃ��锼�a�P�̉~����̓_�o�̂e�ɂ�鑜���o�f�Ƃ���B�n�o�f�̑傫���̍ő�
�@�@�l�ƍŏ��l�����߂�B
�i���j�i�P�j�@�n�o1���i��1�C��1�j���n�o2���i��2�C��2�j���������邱�Ƃ���A��1��2�{��1��2���O
�n�o1�f���i���i��1�|��1�j�C���i��1�{��1�j�j���n�o2�f���i���i��2�|��2�j�C���i��2�{��2�j�j���������邱�Ƃ���A
��2�i��1�|��1�j�i��2�|��2�j�{��2�i��1�{��1�j�i��2�{��2�j���O
��1��2�{��1��2���O�@�Ȃ̂ŁA�@��2�i�|��1��2�|��2��1�j�{��2�i��1��2�{��2��1�j���O�@���A
�@�i��2�|��2�j�i��1��2�{��2��1�j���O
��2�|��2���O�@�Ȃ̂ŁA�@��1��2�{��2��1���O
���̂Ƃ��A�@�������Ɓ���1/��i��12�{��12�j���P/��i�P�{�i��1/��1�j2�j
�����ŁA��1��2�{��1��2���O�@����A��1/��1���|��2/��2
��1��2�{��2��1���O�@����A��1/��1���|��2/��2�@�Ȃ̂ŁA��1/��1����1/��1�@���A�i��1/��1�j2���P
����āA�������Ɓ��P/ �@���A�@�Ɓ���/�S
�@���A�@�Ɓ���/�S
�i�Q�j�@�n�o���i�������ƁC�������Ɓj�@�Ƃ����ƁA�@�n�o�f���i���i�������Ɓ|�������Ɓj�C���i�������Ɓ{�������Ɓj�j
���̂Ƃ��A
�n�o�f����i��2�i�P�|�������Q�Ɓj�{��2�i�P�{�������Q�Ɓj�j����i�i��2�{��2�j�|�i��2�|��2�j�������Q�Ɓj
�������Q�Ɓ��|�P�@���Ȃ킿�A�Ɓ��R��/�S�A�V��/�S�@�̂Ƃ��A�ő�ŁA�ő�l�@ ��
��
�������Q�Ɓ��P�@���Ȃ킿�A�Ɓ���/�S�A�T��/�S�@�̂Ƃ��A�ŏ��ŁA�ŏ��l�@ ���@�@�i�I�j
���@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���Q�P���t��
�@���̓��k��w�@������n�i�P�X�X�R�j�̖����A�P�Ȃ鐬���v�Z�ł���B
����@�@�s��
�@�@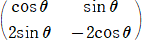 �@�A
�@�A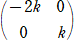
�̕\���P���ϊ������ꂼ��e�A�f�Ƃ���B�e�Ƃf�̍����ϊ��f�e�ɂ���āA�_(�Q�C�Q)���_(�O�C�|�W)
�Ɉڂ�悤�ɁA�Ɓi�O���Ɓ��Q�j�Ǝ������̒l�����߂�B
�i���j�@�e�Ƃf�̍����ϊ��f�e��\���s��́A
�@�@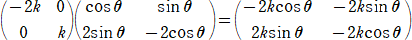
���̂Ƃ��A�_(�Q�C�Q)�͓_�i�|�S���i�������Ɓ{�������Ɓj�C�S���i�������Ɓ|�������Ɓj�j�Ɉڂ����B
��ӂ��A�@�|�S���i�������Ɓ{�������Ɓj���O�@�C�S���i�������Ɓ|�������Ɓj���|�W
��Q�����A�����O�@�Ȃ̂ŁA�@�������Ɓ{�������Ɓ��O�@���Ȃ킿�A�@�������i�Ɓ{��/�S�j���O
��/�S���Ɓ{��/�S���Q�{��/�S�@���A�@�Ɓ{��/�S���A�Q�@����A�Ɓ��R��/�S�A�V��/�S
���i�������Ɓ|�������Ɓj���|�Q�@�ɂ����āA
�@�Ɓ��R��/�S�@�̂Ƃ��A�@���i�P/ �{�P/
�{�P/ �j���|�Q�@���A�@�����|
�j���|�Q�@���A�@�����|
�@�Ɓ��V��/�S�@�̂Ƃ��A�@���i�|�P/ �|�P/
�|�P/ �j���|�Q�@���A�@����
�j���|�Q�@���A�@���� �@�@�i�I�j
�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�T���R�P���t��
�@���̓��k��w�@�O�����n�i�P�X�X�S�j�̖����A�P�Ȃ鐬���v�Z�ł���B
����@�@�s��
�@�@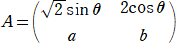 �@�A
�@�A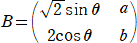
�ɂ����āA�`�͋t�s��`-1�������A�O���Ɓ��P�W�O���A�������O �Ƃ���B
�a���R�`-1�����藧�Ƃ��A���ɓ�����B
�i�P�j�@�`�����߂�B
�i�Q�j�@�`�̕\�� ���� ���ʏ�̂P���ϊ��ɂ���āA�~ ��2�{��2���P �͂ǂ̂悤�Ȑ}�`�Ɉڂ邩�B
�@�@���̕����������߂�B
�i���j�i�P�j�@�a���R�`-1 ���A�@�`�a���R�d�@�i�d�͒P�ʍs��j�@�Ȃ̂ŁA
�@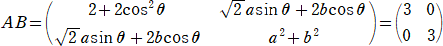
����āA�@�Q�{�Q������2�Ɓ��R�@���A�@�������Ɓ��}�P/
�O���Ɓ��P�W�O������A�@�Ɓ��S�T���@�A�P�R�T��
�Ɓ��S�T���̂Ƃ��A�@ ���������S�T���{�Q���������S�T�����O�@���Ȃ킿�A�@���{
���������S�T���{�Q���������S�T�����O�@���Ȃ킿�A�@���{ �����O
�����O
�@�������O �Ȃ̂ŁA�@���������O�@����́A�@��2�{��2���R�@�ł��邱�Ƃɖ�������̂ŁA�s�K�B
�Ɓ��P�R�T���̂Ƃ��A�@ ���������P�R�T���{�Q���������P�R�T�����O�@���Ȃ킿�A�@���|
���������P�R�T���{�Q���������P�R�T�����O�@���Ȃ킿�A�@���| �����O
�����O
��2�{��2���R�@�ɑ�����āA�@��2���P�@����A�@�����}�P
����āA�@�i���C���j���i �C�P�j�A�i�|
�C�P�j�A�i�| �C�|�P�j�@����A���߂�s��`�́A
�C�|�P�j�@����A���߂�s��`�́A
�@�@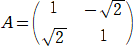 �@�A
�@�A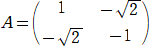
�i�Q�j�@�`�� �q�i�Ɓj�@�i�������A�������Ɓ��}
�q�i�Ɓj�@�i�������A�������Ɓ��} �@�Ə�����B����́A���_�̂܂��Ɋp�Ƃ�
�@�Ə�����B����́A���_�̂܂��Ɋp�Ƃ�
����]���A������ �̑����g���\���P���ϊ��Ȃ̂ŁA�~ ��2�{��2���P �́A�~ ��2�{��2���R
�̑����g���\���P���ϊ��Ȃ̂ŁA�~ ��2�{��2���P �́A�~ ��2�{��2���R
�Ɉڂ����B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�U���Q���t��
�@���̓��k��w�@������n�i�P�X�X�S�j�̖��́A�}�`�I�ɍl����Ɖ����₷���B
����@�@ �������ʂɁA�Ȑ��j�F�i���|���j2/��2�{�R��2/�i��2�|��2�j���P�@�i�O���������j������B���_
�@�@�̂܂��̉�]�s��q�i�Ɓj�̕\���P���ϊ��ɂ���āA�Ȑ��j���}�`�j�f�Ɉڂ����Ƃ���B
�@�@���̂Ƃ��A�j�f���o�i���C���j�b�����O�C���{�����O�p�ƂȂ�悤�ɃƂ͈̔͂��߂�B
�@�@�������A�O�����Ɓ��R�U�O���Ƃ���B
�i���j�@�ȉ~�@�i���|���j2/��2�{�R��2/�i��2�|��2�j���P�@�̒��S�́A�i���C�O�j�ŁA�� ���Ƃ̌�_�́A
�@�i���|���C�O�j�A�i���{���C�O�j�@�ŁA�O���������@���A�@�O�����|�������{���@�ł���B
�@���_��ʂ钼�� �������� ���Ȑ��j�ɐڂ���Ƃ��A���}�ɂ����āA���_�̂܂��ɉ�]�����āA
�Ȑ��j�f���A�j�f���o�i���C���j�b�����O�C���{�����O�p�ƂȂ�悤�ɂ���悢�B
�@�@
�@���������@�������āA�@�i���|���j2/��2�{�R��2��2/�i��2�|��2�j���P�@���Ȃ킿�A
�@�i�R��2��2�{��2�|��2�j��2�|�Q���i��2�|��2�j�{��2�i��2�|��2�j����2�i��2�|��2�j�@����A
�@�i�R��2��2�{��2�|��2�j��2�|�Q���i��2�|��2�j�{�i��2�|��2�j2���O
�ڂ��邱�Ƃ���A���ʎ����c�Ƃ��āA
�@�c/�S����2�i��2�|��2�j2�|�i�R��2��2�{��2�|��2�j�i��2�|��2�j2���O
�������@�Ȃ̂ŁA�@��2�|�i�R��2��2�{��2�|��2�j���O�@���A�@��2���P/�R
����āA�@�����}�P/ �@���A�@�����������i�}�R�O���j
�@���A�@�����������i�}�R�O���j
���̂��Ƃ���A��ӂ������߂ɂ́A�@�P�R�T���{�R�O�����Ɓ��Q�V�O���|�R�O��
���Ȃ킿�A�@�P�U�T�����Ɓ��Q�S�O���@�ƂȂ�B�@�@�i�I�j
�i�R�����g�j�@�ڐ��� �� ���Ƃ̂Ȃ��p���@�}�R�O���ɂȂ�Ƃ́A�v�Z���Ă��Ċ������܂����I
�i�NjL�j�@�ߘa�V�N�U���P�P���t��
�@���̓��k��w�@�O�����n�i�P�X�X�T�j�̖��́A�ܒ~�̂�����ł����B
����@�@�s��
�@�@
�Ƃ���B�`2���p�Ɓi�O���Ɓ��j�̉�]��\���s��ł���A�`����]��\���s��ł��邱
�Ƃ��ؖ�����B
�i���j�@��ӂ��A�@�`2���q�i�Ɓj�@�i�O���Ɓ��j�@�Ȃ̂ŁA�����v�Z���āA
�@��2�{�������������Ɓ@�A�i���{���j�����|�������Ɓ@�A�i���{���j�����������Ɓ@�A�����{��2����������
��P���Ƒ�S������A�@��2����2�@���A�@�����}��
�@�����|���@�̂Ƃ��A�@�������Ɓ��O�@�ƂȂ邪�A�O���Ɓ��@����A�s�K�B����āA������
�@�����ŁA�����O�@�Ƃ���ƁA�������Ɓ��O�@�ƂȂ邪�A�O���Ɓ��@����A�s�K�B
����āA�@�����O�@�ł���B
��Q���Ƒ�R������A�@�Q���i���{���j���O�@���A�@���{�����O�@���Ȃ킿�A�@�����|��
���̂Ƃ��A�@��2�|��2���������Ɓ@���A�@�Q�������|�������Ɓ@�Ȃ̂ŁA
�@�i��2�|��2�j2�{�i�Q�����j2���i��2�{��2�j2���P�@����A�@��2�{��2���P
����āA�@��2���i�P�{�������Ɓj/�Q��������2�i��/�Q�j�@����A�@�����}�������i��/�Q�j
�@��2���i�P�|�������Ɓj/�Q��������2�i��/�Q�j�@����A�@�����}�������i��/�Q�j
�����ŁA�Q�������|�������Ɓ@�Ȃ̂ŁA
�@�����������i��/�Q�j�A�����|�������i��/�Q�j�@�܂��́A
�@�����|�������i��/�Q�j���������i�{��/�Q�j�A�����������i��/�Q�j���|�������i�{��/�Q�j
�ȏォ��A�@�`���q�i��/�Q�j�@�܂��́A�@�`���q�i�{��/�Q�j�@�ƂȂ�A
�@�`�͉�]��\���s��ł���ƌ�����B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�U���Q�U���t��
�@���̓��k��w�@������n�i�P�X�X�T�j�̖��́A�P�Ȃ鐬���v�Z�̖��ł��B
����@�@�s��
�@�@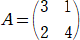
����сA�x�N�g��
�@�@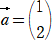 �@�A
�@�A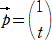
�ɂ��āA���̖�ɓ�����B�������A�����O �Ƃ���B
�i�P�j
�@�@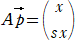
�@�Ƃ���Ƃ��A�s���� �b���|�Q�b���i�Q/�R�j�b���|�Q�b �������B
�i�Q�j�@�b�`���b/�b���b���b�`���b/�b���b �ƂȂ� �� �͈̔͂����߂�B
�i���j�i�P�j�@�������A�@�������{�R�@�A�������S���{�Q�@�Ȃ̂ŁA�@���i���{�R�j���S���{�Q
����āA�@�����i�S���{�Q�j/�i���{�R�j�@���A�@���|�Q���Q�i���|�Q�j/�i���{�R�j�@�Ȃ̂ŁA
�@�b���|�Q�b���i�Q/�i���{�R�j�b���|�Q�b
�����ŁA�����O�@���A�@�Q/�i���{�R�j���Q/�R�@�Ȃ̂ŁA�@�b���|�Q�b���i�Q/�R�j�b���|�Q�b
���Ȃ킿�A�@�b���|�Q�b���i�Q/�R�j�b���|�Q�b �����藧�B
�i�Q�j�@�b�`���b2/�b���b2���i�P�V��2�{�Q�Q���{�P�R�j/�i��2�{�P�j
�܂��A�b�`���b2/�b���b2���P�Q�T/�T���Q�T�@�Ȃ̂ŁA�@�i�P�V��2�{�Q�Q���{�P�R�j/�i��2�{�P�j���Q�T
������A�@�S��2�|�P�P���{�U���O�@���Ȃ킿�A�@�i���|�Q�j�i�S���|�R�j���O�@����A
�@�O�������R/�S�@�A�Q�����@�����߂� �� �͈̔͂ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�U���R�O���t��
�@���̓��k��w�@�O�����n�i�P�X�X�U�j�̖��́A�t�s��Ɋւ�����ł��B
����@�@�O���Ɓ���/�Q �Ƃ��A�s��`��
�@�@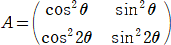
�ɂ���Ē�߂�B�P�ʍs����d�ŕ\���B
�i�P�j�@�s�� �`�|���d �̋t�s���݂��Ȃ��Ƃ��A�� �����߂�B
�i�Q�j�@�i�P�j�ŋ��߂� �� �����ׂĐ��̐��ƂȂ�悤�ȃƂ͈̔͂����߂�B
�i���j�i�P�j�@�������i�`�|���d�j���i������2�Ɓ|���j�i������2�Q�Ɓ|���j�|������2�Ƃ�����2�Q�Ɓ��O�@���A
�@��2�|�i������2�Ɓ{������2�Q�Ɓj���{������2�Ƃ�����2�Q�Ɓ|�i�P�|������2�Ɓj�i�P�|������2�Q�Ɓj���O
���Ȃ킿�A�@��2�|�i������2�Ɓ{������2�Q�Ɓj���{������2�Ɓ{������2�Q�Ɓ|�P���O
�㎮�̍��ӂ́A���|�P �������Ɏ��̂ŁA�@�i���|�P�j�i���{�P�|������2�Ɓ|������2�Q�Ɓj���O
����āA�@�����P�@�A�|�P�{������2�Ɓ{������2�Q��
�i�Q�j�@��ӂ��A�@�|�P�{������2�Ɓ{������2�Q�Ɓ��O�@���Ȃ킿�A�@�S������2�Ƃ�����2�Ɓ�������2��
�O���Ɓ���/�Q �ɂ����āA�@������2�Ɓ��O�@�Ȃ̂ŁA�@������2�Ɓ��P/�S
����ɁA�@�������Ɓ��O�@�Ȃ̂ŁA�@�������Ɓ��P/�Q�@����A�@�O���Ɓ���/�R�@�@�i�I�j
�i�R�����g�j�@��肪��������Ă��܂��ˁI�������܂����B
�i�NjL�j�@�ߘa�V�N�V���P�T���t��
�@���̓��k��w�@������n�i�P�X�X�U�j�̖��́A�P���Ȑ����v�Z�ł���B
����@�@�s��
�@�@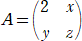 �@�A
�@�A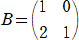 �@�A
�@�A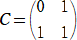
�ɑ��āA���� �`2�a���a�`2�A�`�b���b�` �����藧�Ƃ��A���A���A�� �̒l�����߂�B
�i���j�@�����v�Z���āA
�@�`2�a���a�`2�@���A�@�Q���{�������O�@�A��2���S
�@�`�b���b�`�@���A�@�������@�A�����Q�{���@�A�����Q�{��
�@�Q���{�������O�@����A�@�����O�@�܂��́@�����|�Q
�����O�@�̂Ƃ��A�@�����O�@�A�����Q
�����|�Q�@�̂Ƃ��A�@���������|�S�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�V���P�V���t��
�@���̓��k��w�@������n�i�P�X�X�U�j�̖��́A�P���ϊ��̖��ł���B
����@�@�P���ϊ��e�ɂ��~�b1�F(���|�Q)2�{��2���P�̑����~�b2�F��2�{�i���|���j2���S (�����O�j��
�@�@��v����Ƃ��A�e��\���s��`����� �� �̒l�����߂�B
�i���j�@��ӂ��A���߂�P���ϊ��e�́A���_���S�̂X�O����]�Ƒ�����Q�̑����g�傩�A��
�@���́A������ �Ɋւ���Ώ̈ړ��Ƒ�����Q�̑����g��ł���B
����āA
�@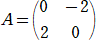 �@�@�܂��́A�@
�@�@�܂��́A�@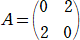
����̏ꍇ���A�@�����S�@�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�W���P�U���t��
�@���̓��k��w�@�O�����n�i�P�X�X�W�j�̖��́A�n�~���g���E�P�[���[�̒藝��������
�ł���B
����@�@�Q�������s��
�@�@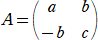
�ɑ��āA�Ίp�����̘a�@Tr�i�`�j��Tr�i�`2�j���|�P �ł���Ƃ���B
�i�P�j�@�`3���d �������B�������A�d�͒P�ʍs��ł���B
�i�Q�j�@�A���P�������� �i�`�{�d�j4���i���@���j�����i���@�|���j �������B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{���j�`�{�i�����{��2�j�d���n
���� Tr�i�`�j���|�P�@���A�@���{�����|�P�@�Ȃ̂ŁA�@�`2�{�`�{�i�����{��2�j�d���n
���̂Ƃ��A�@Tr�i�`2�j���|���|�i�����{��2�j�|���|�i�����{��2�j���P�|�Q�i�����{��2�j���|�P
����āA�@�����{��2���P�@����A�@�`2�{�`�{�d���n�@�Ȃ̂ŁA
�@�`3�|�d���i�`�|�d�j�i�`2�{�`�{�d�j���O�@����A�`3���d �����藧�B
�i�Q�j�@�i�P�j�@���A�@�`�{�d���|�`2�@����A�@�i�`�{�d�j2���`4���`�@�Ȃ̂ŁA
�@�i�`�{�d�j4���`2���|�`�|�d�@���A
�@�������i�i�`�{�d�j4�j���i���{�P�j�i���{�P�j�{��2�������{��2�{���{���{�P���P���O�@�Ȃ̂ŁA
�@�i�`�{�d�j4 �͋t�s������B���̂Ƃ��A�@�������@�A������2�|��2�@�����ƂȂ�B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�W���Q�X���t��
�@���̓��k��w�@������n�i�P�X�X�W�j�̖��́A�����v�Z�̖��ł���B
����@�@�s��
�@�@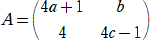
�ɂ����āA���A���A�� �͂��ׂĐ����ł���A�`2���d �i�d�͒P�ʍs��j�Ƃ���B
�i�P�j�@�� ����� �� �� �� �̎��ŕ\���B
�i�Q�j�@�s��
�@�@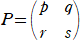
�����݂��āA
�@�@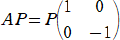
�����藧�Ƃ��A�s��o�̐����� �� �̎��ŕ\���B�������A���A���A���A�� �͂��ׂĐ����ŁA
�����|�������P �Ƃ���B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A
�@�`2�|�S�i���{���j�`�{�i�i�S���{�P�j�i�S���|�P�j�|�S���j�d���n
�@�`2���d ���A�@�S�i���{���j�`���i�i�S���{�P�j�i�S���|�P�j�|�S���{�P�j�d
����āA�@�P�U�i���{���j���O�@����A�@�����|���@�ŁA�i�S���{�P�j�i�S���|�P�j�|�S���{�P���O
���Ȃ킿�A�@�S�����|�i�S���{�P�j2�{�P���|�P�U��2�|�W���@���A�@�����|�S��2�|�Q��
�i�Q�j�@�������A
�@�@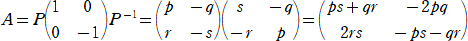
�Ȃ̂ŁA������r���āA
�@�S���{�P�������{�����@�A�|�S��2�|�Q�����|�Q�����@�A�S���Q����
���Ȃ킿�A�@�S���{�P�������{�����@�A�Q��2�{���������@�A�Q������
���A�� �͐����Ȃ̂ŁA�@�i���C���j���i�P�C�Q�j�A�i�Q�C�P�j�A�i�|�P�C�|�Q�j�A�i�|�Q�C�|�P�j
�i���C���j���i�P�C�Q�j�̂Ƃ��A�@�Q���{�����S���{�P�@�A�������Q��2�{��
�@�����������āA�@�Q��2�|�i�S���{�P�j���{�Q��2�{�����O�@���A�@�i�Q���|�Q���|�P�j�i���|���j���O
�@����āA�@�����i�Q���{�P�j/�Q�@�A���@�ŁA���͐����Ȃ̂ŁA�@�������@�A�����Q���{�P
�@���̂Ƃ��A�@�����|�������|�P�@�ŁA�����ɔ����邩��s�K�B
�i���C���j���i�Q�C�P�j�̂Ƃ��A�@���{�Q�����S���{�P�@�A�������Q��2�{��
�@�����������āA�@�Q��2�|�i�S���{�P�j���{�Q��2�{�����O�@���A�@�i�Q���|�Q���|�P�j�i���|���j���O
�@����āA�@�����i�Q���{�P�j/�Q�@�A���@�ŁA���͐����Ȃ̂ŁA�@�����Q���{�P�@�A������
�@���̂Ƃ��A�@�����|�������P�@�ŁA���������B
�i���C���j���i�|�P�C�|�Q�j�̂Ƃ��A�@�|�Q���|�����S���{�P�@�A�������Q��2�{��
�@�����������āA�@�Q��2�{�i�S���{�P�j���{�Q��2�{�����O�@���A�@�i�Q���{�Q���{�P�j�i���{���j���O
�@����āA�@�����|�i�Q���{�P�j/�Q�@�A�|���@�ŁA���͐����Ȃ̂ŁA�@�����|���@�A�����|�Q���|�P
�@���̂Ƃ��A�@�����|�������|�P�@�ŁA�����ɔ����邩��s�K�B
�i���C���j���i�|�Q�C�|�P�j�̂Ƃ��A�@�|���|�Q�����S���{�P�@�A�������Q��2�{��
�@�����������āA�@�Q��2�{�i�S���{�P�j���{�Q��2�{�����O�@���A�@�i�Q���{�Q���{�P�j�i���{���j���O
�@����āA�@�����|�i�Q���{�P�j/�Q�@�A�|���@�ŁA���͐����Ȃ̂ŁA�@�����|�Q���|�P�@�A�����|��
�@���̂Ƃ��A�@�����|�������P�@�ŁA���������B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�X���Q�P���t��
�@���̓��k��w�@������n�i�P�X�X�X�j�̖��́A�����v�Z�̖��ł���B
����@�@�i�P�j�@�����𐬕��Ƃ���Q�������s��
�@�@
������������A���i�����O�j�ɂ��āA
�@�@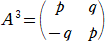
�����A�������@�A�����|���@�ł��邱�Ƃ������B
�i�Q�j�@�����𐬕��Ƃ���Q�������s��
�@�@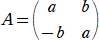
�ŁA
�@�@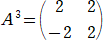
�������̂����ׂċ��߂�B
�i���j�i�P�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�i���{���j�`�{�i�����|�����j�d���n
�����A�@�`2���i���{���j�`�|�i�����|�����j�d�@���A
�@�`3���i���{���j�`2�|�i�����|�����j�`���i���{���j�i�i���{���j�`�|�i�����|�����j�d�j�|�i�����|�����j�`
�@���o�i���{���j2�|�i�����|�����j�p�`�|�i���{���j�i�����|�����j�d
����āA������r���āA
�@�������o�i���{���j2�|�i�����|�����j�p�|�i���{���j�i�����|�����j�@�A�������o�i���{���j2�|�i�����|�����j�p
�|�������o�i���{���j2�|�i�����|�����j�p�@�A�������o�i���{���j2�|�i�����|�����j�p�|�i���{���j�i�����|�����j
���̂Ƃ��A�@�i���|���j�o�i���{���j2�|�i�����|�����j�p���O�@�A�i���|���j�o�i���{���j2�|�i�����|�����j�p���Q��
�@�i���{���j�o�i���{���j2�|�i�����|�����j�p���O
�������A�@�����O�@�Ȃ̂ŁA�@�i���{���j2�|�i�����|�����j���O
����āA�@���|�����O�@�A�@���{�����O�@���A�@�������@�A�����|���@�ƂȂ�B
�i�Q�j�@�n�~���g���E�P�[���[�̒藝���A�@�`2�|�Q���`�{�i��2�{��2�j�d���n �Ȃ̂ŁA
�@�`3���Q���i�Q���`�|�i��2�{��2�j�d�j�|�i��2�{��2�j�`���i�R��2�|��2�j�`�|�Q���i��2�{��2�j�d
����āA������r���āA
�@���i�R��2�|��2�j�|�Q���i��2�{��2�j���Q�@�A���i�R��2�|��2�j���Q
���Ȃ킿�A�@��3�|�R����2���Q�@�A�R��2���|��3���Q ���A�@��3�|�R����2���R��2���|��3
���ӂ���3�Ŋ����āA�@�i��/���j3�|�R�i��/���j���R�i��/���j2�|�P�@����A
�@�i��/���{�P�j�i�i��/���j2�|�S�i��/���j�{�P�j���O
����������āA�@��/�����|�P�@�A�Q�} �@�ƂȂ�B
�@�ƂȂ�B
�@��/�����|�P�@�̂Ƃ��A�@�����|���@�ŁA�@��3���|�P�@���A�@�����|�P�@�A�����P
�@��/�����Q�} �@�̂Ƃ��A�@�����i�Q�}
�@�̂Ƃ��A�@�����i�Q�} �j���@����A�@�i�Q�}
�j���@����A�@�i�Q�} �j���E�i�i�V�}�S
�j���E�i�i�V�}�S �j�|�R�j��2���Q
�j�|�R�j��2���Q
�@����āA�@�i�Q�} �j�i�Q�}�Q
�j�i�Q�}�Q �j��3���P ���A�@�i�S�}�Q
�j��3���P ���A�@�i�S�}�Q �j�i�P�}
�j�i�P�} �j��3���P
�j��3���P
���Ȃ킿�A�@�i�P�} �j3��3���P ����A�@�����P/�i�P�}
�j3��3���P ����A�@�����P/�i�P�} �j���i�|�P�}
�j���i�|�P�} �j/�Q
�j/�Q
���̂Ƃ��A�@�����i�P�} �j/�Q�@�@�i�I�j
�j/�Q�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�X���Q�U���t��
�@���̓��k��w�@�O�����n�i�Q�O�O�O�j�̖��́A�����v�Z�̖��ł���B
����@�@
�@�@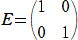 �@�A
�@�A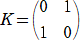 �@�Ƃ��A���A���������Ƃ���B
�@�Ƃ��A���A���������Ƃ���B
�i�P�j�@�i���d�{���j�j2�����d�{���j�ƂȂ���� ���A�� �����݂��邽�߂ɂ́A���A�� ���ǂ�ȏ�����
�@�@���������Ƃ��K�v�\���ł��邩�B
�i�Q�j�@���A�� �� ��2�{��2���Q �����A����ɁA
�@�@�i���d�{���j�j2�����d�{���j�@�A�i���d�{���j�j2�����d�|���j
�@�@�ƂȂ���� ���A���A���A�� �����݂���Ƃ���B���̂Ƃ��A���A�� �̒l�����߂�B
�i���j�i�P�j�@�j2���d �Ȃ̂ŁA�@�i���d�{���j�j2����2�d�{�Q�����j�{��2�d���i��2�{��2�j�d�{�Q�����j
�@����āA�@��2�{��2�����@�A�Q���������@���Ȃ킿�A�@��2��2����2/�S
���̂Ƃ��A��2�A��2 �́A�Q�������� ��2�|�����{��2/�S���O�@�̂Q�̔̎������ƂȂ�̂ŁA
�@���̕����� ������/�Q �ɂ��āA
�@�����O�@�̂Ƃ��A�@�����O
�@�����O�@�̂Ƃ��A�@���ʎ��c����2�|��2���O�@���@��2���O
�ȏォ��A���A�����������ׂ������́A�@���������O�@�܂��́@�i�����O�@���@��2����2�j
�@�@
�i�Q�j�@�i���d�{���j�j2�����d�{���j ���A�i�P�j����A���������O�@�܂��́@�i�����O�@���@��2����2�j
�i���d�{���j�j2�����d�|���j �ɂ��Ă����l�ɂ��āA���������O�@�܂��́@�i�����O�@���@��2����2�j
�@���A�� �� ��2�{��2���Q �����̂ŁA��2���P�@���Ȃ킿�A�@�����P�@���̂Ƃ��A�@�����P�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P�O���Q�W���t��
�@���̓��k��w�@������n�i�Q�O�O�P�j�̖����A�����v�Z�̖��ł���B
����@�@ ���A���A�� �͎����ŁA�����P�A������ �Ƃ���B�s��
�@�@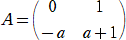 �@�A
�@�A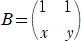 �@�A
�@�A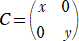
�́A�`�a���a�b �����Ƃ���B
�i�P�j�@�a�� �� ��p���ĕ\���B
�i�Q�j�@�a-1 ����т`n �i�����P�A�Q�A�R�A�E�E�E�j�� �� ��p���ĕ\���B
�i�R�j�@����o��n�p���A��0�����A��1�����A
�@�@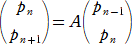 �@�@�i�����P�A�Q�A�R�A�E�E�E�j
�@�@�i�����P�A�Q�A�R�A�E�E�E�j
�ɂ���Ē�߂�B�o��n�p���������邽�߂� ���A���A�� �̏��������߂�B
�@�܂��A���̂Ƃ��̋Ɍ� ������������ ��n �����߂�B
�i���j�i�P�j�@�`�a���a�b �̐����v�Z����A
�@�|���{�i���{�P�j������2�@�A�|���{�i���{�P�j������2
���Ȃ킿�A�@�i���|���j�i���|�P�j���O�@�A�i���|���j�i���|�P�j���O�@����A
�@�������A�P�@�������A�P
�����ŁA�����P�A������ �Ȃ̂ŁA�@�����P�@�A������
����āA
�@�@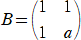
�i�Q�j�@�������a�����|�P���O�@�Ȃ̂ŁA�a�͋t�s��������A
�@�@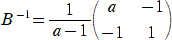
�@�`�a���a�b ���A�@�`���a�b�a-1�@�Ȃ̂ŁA�@�`�����a�b���a-1�@�ƂȂ�B
�@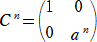
�@�Ȃ̂ŁA
�@�@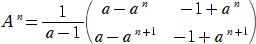
�i�R�j�@�������A
�@�@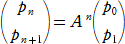
����A�@�������o�i���|�����j���{�i�����|�P�j���p/�i���|�P�j���o�����|���{�i���|���j�����p/�i���|�P�j
�o��n�p���������邽�߂ɂ́A�@�������@�܂��́@�|�P�������P�@���K�v�\�������ł���B
���̂Ƃ��A�@������������ ��n���i�����|���j/�i���|�P�j�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P�P���P�S���t��
�@���̓��k��w�@������n�i�Q�O�O�Q�j�̖����A�����v�Z�̖��ł���B
����@�@ �d��P�ʍs��Ƃ���B���A���A�� �͎����Ƃ��A�s��A���A�`3���d���݂����A����Ɏ���
�@�@����
�@�@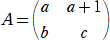 �@�A
�@�A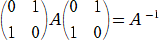
�����Ƃ���B���̂悤�Ȃ`�����ׂċ��߂�B
�i���j�@�`3���d ���A�`-1���`2 �Ȃ̂ŁA�����v�Z���āA
�@������2�{���i���{�P�j�@�A�����i���{�P�j�ia�{���j�@�A���{�P�����i���{���j�@�A�������i���{�P�j�{��2
��P���Ƒ�S������A�@���|������2�|��2�@���Ȃ킿�A�@�i���|���j�i���{���{�P�j���O
�@����āA�@���|�����O�@�܂��́@���{���{�P���O
�@�����ŁA�@���|�����O�@���Ȃ킿�A�@�������@�Ƃ���ƁA
�@������2�{���i���{�P�j�@�A�����Q���i���{�P�j�@�A���{�P���Q����
��Q���������āA�@���{�P���S��2�i���{�P�j�@����A�@�����|�P�@�܂��́@�����}�P/�Q
�@�����|�P�@�̂Ƃ��A��P������@�|�P���P�@�ƂȂ�A����͖����B
�@�����P/�Q�@�̂Ƃ��A�@�����R/�Q�@�ŁA��P������A�@�P/�Q���P/�S�{�X/�S���T/�Q�@�ƂȂ�A�����B
�@�����|�P/�Q�@�̂Ƃ��A�@�����|�P/�Q�@�ŁA��P������A�|�P/�Q���P/�S�|�P/�S���O�@�ƂȂ�A�����B
�ȏォ��A���|�����O�@�Ȃ̂ŁA�@���{���{�P���O�@���̂Ƃ��A
�@������2�|�����@�A�����|���ia�{���j�@�A�|�������i���{���j�@�A�����|�����{��2
�����ŁA�@���{�����|�P�@�Ȃ̂ŁA��Q���A��R�����A�@������
�@��S�����A�@�|���|�P���|��2�{��2���O�@�Ȃ̂ŁA�@�����|�P�@���Ȃ킿�A�@�����|�P�A�����O
�ȏォ��A���߂�s��`�́A
�@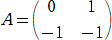
�@���̍s��`�͗^����ꂽ���������B�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P�P���Q�P���t��
�@���̓��k��w�@�O�����n�i�Q�O�O�R�j�̖����A�����v�Z�̖��ł���B
����@�@ ���� ���A���A���A�� �ɑ��A�d��P�ʍs��Ƃ��A
�@�@ �@�A
�@�A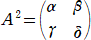 �@�A
�@�A
�Ƃ����B
�i�P�j�@���|�������O �������B
�i�Q�j�@�`���A�`4���d �����Ȃ�A�`2���d�@�܂��́@�`2���|�d�@�ƂȂ邱�Ƃ������B
�i�R�j�@�`���A�`2���|�d�@����с@�j�`���|�`�j�@�����Ƃ��A���A���A�� �� �� �̎��ŕ\���B
�@�܂��A���̂Ƃ��A�`�j���`m�j�`n�@����������悤�Ȑ����̑g(���C��)�ŁA
�@�P�������R�A�P�������R�@�͈̔͂ɂ�����̂����ׂċ��߂�B
�i���j�i�P�j�@���|�������i��2�{�����j�i�����{��2�j�|�����ia�{���j2���i�����|�����j2���O�@�ł���B
�i�Q�j�@�`4���d ���A
�@��2�{�������P�@�A�i���{�j�����O�@�A�i���{�j�����O�@�A�����{��2���P
�@��P���Ƒ�S������A�@��2����2�@���Ȃ킿�A�@�i���|�j�i���{�j���O
�@���{���O�@�̂Ƃ��A�@���|���@�ŁA�@�|��2�|�������O�@���Ȃ킿�A�@��2�{�������O
�@����́A��2�{�������P�@�ɖ�������B����āA���{���O�@�ƂȂ�A���̂Ƃ��A�@������
�@����ɁA�����O�@�A�����O�@�ł���B���̂Ƃ��A�@��2���P�@�A��2���P
���{���O�@�ɒ��ӂ��āA�@�i���C�j���i�P�C�P�j�A�i�|�P�C�|�P�j
�ȏォ��A�@�`2���d�@�܂��́@�`2���|�d�@�ƂȂ�B
�i�R�j�@�j�`���|�`�j�@���A�@�����|���@�A�����|��
�@�`2���|�d�@���A�@��2�{�������|�P�@���Ȃ킿�A��2�|��2���|�P�@���A�@�����}��i��2�{�P�j
�@����āA�@������i��2�{�P�j�@�̂Ƃ��A�����|��i��2�{�P�j
�@�@�����|��i��2�{�P�j�@�̂Ƃ��A������i��2�{�P�j
�܂��A�@�����|���@�ƕ\�����B
�@�`2���|�d�@���A�`4���d �ŁA�`m �ɂ��ċN���肤��ꍇ�͎��̒ʂ�ł���B
�@���߂O�@�i�������@�S�j�̂Ƃ��A�`m�߂d
�@���߂P�@�i�������@�S�j�̂Ƃ��A�`m�߂`
�@���߂Q�@�i�������@�S�j�̂Ƃ��A�`m�߁|�d
�@���߂R�@�i�������@�S�j�̂Ƃ��A�`m�߁|�`
�ȏォ��A�P�������R�A�P�������R�@�͈̔͂ŁA�`m�j�`n�@�́A�`2���|�d�@����с@�j�`���|�`�j
�ɒ��ӂ��āA
�����P�A�����P�@�̂Ƃ��A�@�`m�j�`n���`�j�`���|�`2�j���j
�����P�A�����Q�@�̂Ƃ��A�@�`m�j�`n���|�`�j�d���|�`�j
�����P�A�����R�@�̂Ƃ��A�@�`m�j�`n���|�`�j�`���`2�j���|�d�j���|�j
�����Q�A�����P�@�̂Ƃ��A�@�`m�j�`n���|�d�j�`���|�j�`���`�j
�����Q�A�����Q�@�̂Ƃ��A�@�`m�j�`n���d�j�d���j
�����Q�A�����R�@�̂Ƃ��A�@�`m�j�`n���d�j�`���j�`���|�`�j
�����R�A�����P�@�̂Ƃ��A�@�`m�j�`n���|�`�j�`���`2�j���|�j
�����R�A�����Q�@�̂Ƃ��A�@�`m�j�`n���`�j
�����R�A�����R�@�̂Ƃ��A�@�`m�j�`n���`�j�`���|�`2�j���j
�ȏォ��A�`�j���`m�j�`n�@����������悤�Ȑ����̑g(���C��)�́A
�@(���C��)��(�Q�C�P)�A(�R�C�Q)�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P�Q���U���t��
�@���̓��k��w�@������n�i�Q�O�O�R�j�̖����A�����v�Z�̖��ł���B
����@�@�Q���̐����s��`�A�a�� �`2���a2���n (�n�͗�s��) �����Ƃ���B���́i�P�j�i�Q�j
�@�@�������B
�i�P�j�@(�`�{�a)2�����d�@(���͎����A�d�͒P�ʍs��)
�i�Q�j�@�i�`�{�a�j2���n�@�A�`���n �Ȃ�ρA�a�����`�@(���͎���) �����藧�B
�i���j�i�P�j�@
�@�@
�Ƃ����ƁA�`2���n�@����A�@��2�{�������O�@�A�i���{���j�����O�@�A�i���{���j�����O�@�A�����{��2���O
��P���Ƒ�S������A�@��2����2�@���Ȃ킿�A�@�i���{���j�i���|���j���O
�@���{�����O�@�̂Ƃ��A��Q���Ƒ�R������A���������O�@���A��2����2���O�@�����A���������O
�@������ɁA����͖����ł���B����āA���{�����O�@���Ȃ킿�A�@�����|��
�@����āA
�@�@�@�@�@
���l�ɂ��āA
�@�@�@
�Ƃ����ƁA�a2���n�@����A�@��2�{�������O�@�A�i���{���j�����O�@�A�i���{���j�����O�@�A�����{��2���O�@����A
�@
���̂Ƃ��A(�`�{�a)2��(�`�{�a)(�`�{�a)���`�a�{�a�`�@����A
�@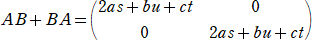
�@���������āA�@�Q�����{�����{���������@�Ƃ����A
�@(�`�{�a)2���`�a�{�a�`�����d�@(���͎����A�d�͒P�ʍs��)
�Ə�����B
�i�Q�j�@�i�`�{�a�j2���n�@���A�@�����Q�����{�����{�������O
�@��2�{�������O�@�A�i���{���j�����O�@�A�i���{���j�����O�@�A�����{��2���O�@����A
�@�����O�@�̂Ƃ��A�@��2���O�@���Ȃ킿�A�@�����O
�@�`���n�@����A�@�����O�@�ł���B���̂Ƃ��A�Q�����{�����{�������������O�@����A�����O
�@���̂Ƃ��A��2�{�������O�@�A�i���{���j�����O�@�A�i���{���j�����O�@�A�����{��2���O�@����A
��2���O�@���Ȃ킿�A�@�����O
�@����āA
�@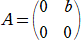 �@�A
�@�A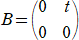
�Ə�����̂ŁA������/���@�Ƃ����A�a�����`�@(���͎���) �Ə����邱�Ƃ�������B
�@�����O�@�̂Ƃ��A�@��2���O�@���Ȃ킿�A�@�����O
�@�`���n�@����A�@�����O�@�ł���B���̂Ƃ��A�Q�����{�����{�������������O�@����A�����O
�@���̂Ƃ��A��2�{�������O�@�A�i���{���j�����O�@�A�i���{���j�����O�@�A�����{��2���O�@����A
��2���O�@���Ȃ킿�A�@�����O
�@����āA
�@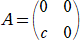 �@�A
�@�A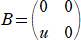
�Ə�����̂ŁA������/���@�Ƃ����A�a�����`�@(���͎���) �Ə����邱�Ƃ�������B
�@�����O�@���@�����O�@�̂Ƃ��A��2���|�������O�@����A�@�����O�@�ł���B
�@���̂Ƃ��A�@�Q�����{�����{�������O�@���A�@�����|�i�����{�����j/�i�Q���j
�@��2�{�������O�@�ɑ�����āA�@�i�����{�����j2/�i�S��2�j�{�������O
���Ȃ킿�A�@��2��2�{�Q���������{��2��2�{�S��2�������O
�@��2���|�����@���A�@��2��2�{�Q���������{��2��2�|�S�����������O�@�Ȃ̂ŁA
�@��2��2�|�Q���������{��2��2���O�@���Ȃ킿�A�@�i�����|�����j2���O�@����A�@����������
�����ŁA�@���������������@�Ƃ����ƁA�@�����|�i�����{�����j/�i�Q���j���|��/���@�A������/���@�A������/��
����āA
�@�@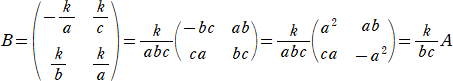
�ƂȂ�̂ŁA���̏ꍇ���A������/�����@�Ƃ����A�a�����`�@(���͎���) �Ə����邱�Ƃ�������B
�ȏォ��A�i�`�{�a�j2���n�@�A�`���n �Ȃ�ρA�a�����`�@(���͎���) �����藧�B�@�@�i�I�j
�i�R�����g�j�@�Ȃ��Ȃ��n�[�h�Ȑ����v�Z�ł����B
�@�@�ȉ��A�H�����I

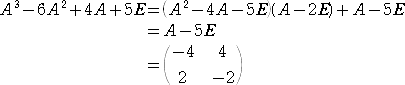
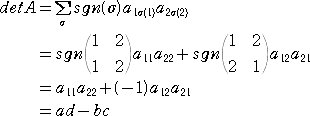

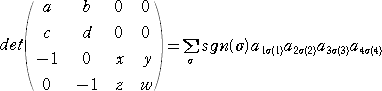
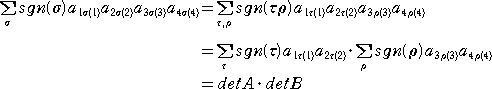
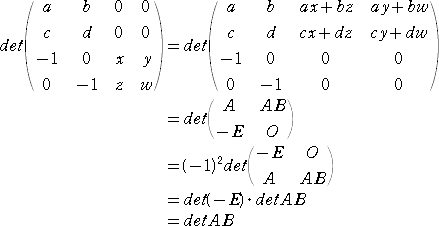 �i�؏I�j
�i�؏I�j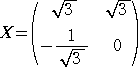
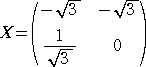

 �@�@�i�I�j
�@�@�i�I�j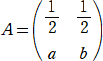
 �@�@�i�I�j
�@�@�i�I�j

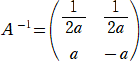
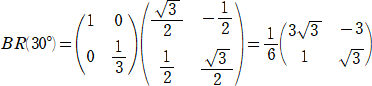
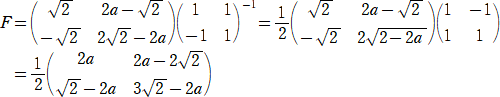
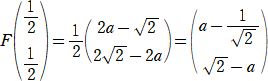
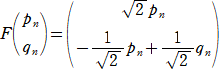
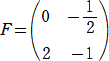
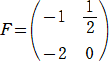 �@�@�i�I�j
�@�@�i�I�j