
行列の対角化とか、Jordanの標準形、2次曲線(曲面)の分類など、固有値、固有ベクトル
の活躍する場は数多い。このページでは、簡単に固有ベクトルを求める裏技を紹介したい。
定義 実数体R上の線形空間をVとする。VからVへの線形変換を表す行列Aに対して、
Ax=kx (xは0以外)となるRの要素kを、Aの固有値、Vの要素xをkに属するAの
固有ベクトルという。
固有ベクトルを求める 
行列の対角化とか、Jordanの標準形、2次曲線(曲面)の分類など、固有値、固有ベクトル
の活躍する場は数多い。このページでは、簡単に固有ベクトルを求める裏技を紹介したい。
定義 実数体R上の線形空間をVとする。VからVへの線形変換を表す行列Aに対して、
Ax=kx (xは0以外)となるRの要素kを、Aの固有値、Vの要素xをkに属するAの
固有ベクトルという。
| 例 | |
に対して、固有方程式 det(A−kE)=0 を解くと、k=1、5 |
| このとき、(A−E)(A−5E)= | =0 (但し、Eは単位行列) |
(A−E)(A−5E)=(A−E)(u v) (ただし、u、v は、A−5E の列ベクトル)
右辺を計算して、 (A−E)(A−5E)=(A−E)(u v)=((A−E)u (A−E)v)= 0
なので、 (A−E)v=0 となり、 A−5E の列ベクトル v が、固有値 1 に属する
固有ベクトルになることが分かる。固有値 5 に属する固有ベクトルの求め方も同様。
| したがって、、k=1に属する固有ベクトル(の一つ)は、 | |
| k=5に属する固有ベクトル(の一つ)は、 |
(注意) 固有ベクトルを求める正統的な方法は、不定な連立方程式を解かなければならな
い。たとえば、上記の例では、k=1のとき、連立方程式
2x+3y=x , x+4y=y の解は、x+3y=0 を満たす全てのx,y
となる。
このことから、固有ベクトルが求められる。k=5のときも、同様。
正統的な解法に比べて、裏技の解法は、単に行列の成分計算に帰着されているので、容
易に、固有ベクトルが求められることに驚かされる。
(参考文献:宮原 繁 著 漸化式 (科学新興社モノグラフ))
(追記) 山梨県在住のKさんという方からメールで質問を頂いた。
上記の裏技は、行列が3次や4次、・・・の場合も使えるのでしょうか?
もう随分昔に学んだ線形代数学の知識しかないので、確定的なことをいうだけの自信は
ありませんが、多分、同様に裏技が使えるはずです。
その根拠として、
(1) 任意の n 次の正方行列 A に対して、適当な正則行列 P を選ぶことにより、
P-1APを上三角行列に変形することができる。
このとき、対角成分は、Aの固有値である。
(2) 行列 A の固有多項式 FA(X)=det(XE−A) (Eは単位行列) に対して、
FA(A)=O (O は零行列) が成り立つ。(Hamilton−Cayley の定理)
があげられる。 (1)(2)より、行列 A の固有値を α、β、・・・、γ とすれば、
(A−αE)(A−βE)・・・・・・(A−γE)=O
が成り立つ。
いくつか具体例を通して、固有値と固有ベクトルを裏技で求めてみよう。
裏技で得られたものが、本当に題意に適するかどうかは、読者の検証にまかせようと思う。
例 次の行列 A の固有値と固有ベクトルを求めよ。

det(A−λE)=−λ(λ−1)(λ−2)=0 より、固有値は、 0 ,1 ,2 の3個。
このとき、 A(A−E)(A−2E)=O が成り立ち、
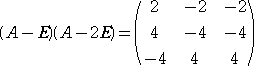
したがって、上記行列の列ベクトルに注目すれば、
固有値 0 に属する固有ベクトル(の一つ)は、 ( 1 , 2 ,−2
) である。
同様にして、
固有値 1 に属する固有ベクトル(の一つ)は、 ( 1 , 2 ,−1
) である。
固有値 2 に属する固有ベクトル(の一つ)は、 ( 0 , 1 ,−1
) である。
例 次の行列 A の固有値と固有ベクトルを求めよ。
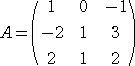
det(A−λE)=(λ−3)(λ2−λ+1)=0 より、
固有値は、 3 ,α ,β の3個。
ただし、α=(1+![]() i)/2 、β=(1−
i)/2 、β=(1−![]() i)/2 である。 ( i は虚数単位)
i)/2 である。 ( i は虚数単位)
このとき、 (A−3E)(A−αE)(A−βE)=(A−3E)(A2−A+E)=O が成り立ち、
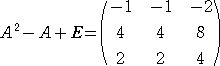
したがって、上記行列の列ベクトルに注目すれば、
固有値 3 に属する固有ベクトル(の一つ)は、 ( −1 , 4 ,2
) である。
同様にして、
(A−αE)(A−3E)(A−βE)=(A−αE)(A2−(β+3)A+3βE)=O が成り立ち、
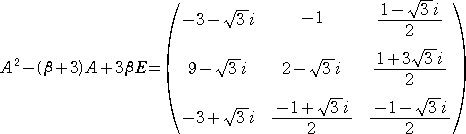
したがって、上記行列の列ベクトルに注目すれば、
固有値 α に属する固有ベクトル(の一つ)は、
( 2 , −4+2![]() i ,1−
i ,1−![]() i )
i )
である。同様にして、固有値 β に属する固有ベクトル(の一つ)は、
( 2 , −4−2![]() i ,1+
i ,1+![]() i )
i )
である。
上記で述べたことが、Kさんの質問の趣旨に合致していることを祈って筆をおく。
(追記) 平成26年6月24日付け
この頁の冒頭で、固有ベクトルを簡便に求める方法を紹介したが、行列の対角化を用いて、
いろいろな応用に活用できることを次の書籍で学んだ。
橋口 正 著 「行列の対角化の『簡便法』とその応用について」
(数研通信 No.78 (数研出版))
それによると、行列
![]()
の固有値を、α、β(ただし、α、βは0でない相異なる実数)とすれば、
![]()
| と置くことにより、 P-1AP= | と、行列Aを対角化することができる。 |
すなわち、固有値α、βのそれぞれに属する固有ベクトルを u、v とすると、
P=(v u) v=t(a−α c) 、 u=t(b d−β) (t は転置行列を表す)
と書けることを意味する。
| 例 | |
に対して、固有方程式 det(A−kE)=0 を解くと、k=1、5 |
このとき、上記の公式によれば、
固有値5に属する固有ベクトルvは、v=t(2−1 1)=t(1 1)
固有値1に属する固有ベクトルuは、u=t(3 4−5)=t(3 −1)
であることが分かる。
証明は、冒頭で述べたことから明らかだろう。ここで、Pは次の豊かな性質を持つ。
P2=−(detP)E (Eは単位行列) なので、 P-1AP=PAP-1 が成り立ち、
| PA | = | P |
(証明) α、βは固有方程式 x2−(a+d)x+ad−bc=0 の解なので、解と係数の関係
より、
α+β=a+d 、 αβ=ad−bc
よって、 Tr(P)=a−α+d−β=0 なので、ハミルトン・ケーリーの定理より、
P2−Tr(P)P+det(P)E=0 すなわち、 P2+det(P)E=0
したがって、 P2=−det(P)E が成り立つ。このとき、 P-1=−(1/det(P))P である。
よって、 P-1AP=−(1/det(P))PA・(−det(P))P-1=PAP-1 が成り立つ。
| このとき、 | PA | = | P | となる。 (証終) |
上記の公式が、いろいろな応用の基本となる。
例 連立型の漸化式
x1=2 、y1=1 、xn+1=2xn+3yn 、yn+1=xn+4yn (n=1、2、・・・)
について、通常は、行列の対角化からの行列のn乗計算で求めるのが定石であろう。
上記の公式を用いると、やや気が重い行列のn乗計算をしなくとも軽妙に一般項が求めら
れる。
|
このとき、P=(v u) v=t(1 1)、u=t(3 −1) により、
| PA | = | P より、PXn+1= | PXn |
が成り立つので、 xn+1+3yn+1=5(xn+3yn) 、xn+1−yn+1=xn−yn ・・・ (*) が直ちに
得られる。これより、 xn+3yn=5n-1(x1+3y1)=5n 、xn−yn=x1−y1=1 なので、
xn=(5n+3)/4 、 yn=(5n−1)/4
(コメント) この公式を用いると、要の関係式(*)が暗算で求められますね!感動しました。
以下、工事中!