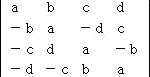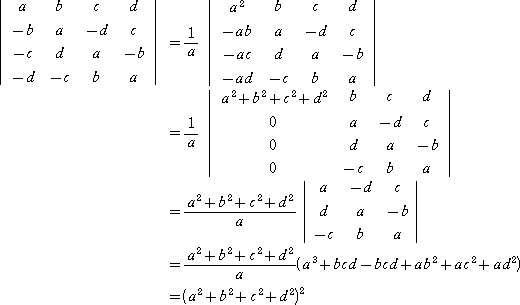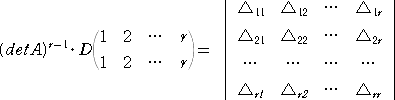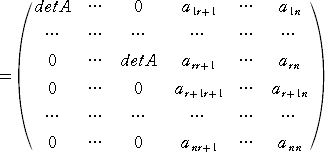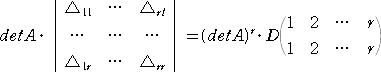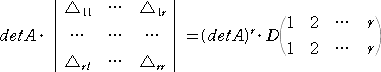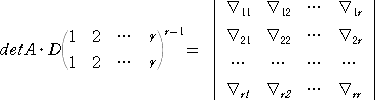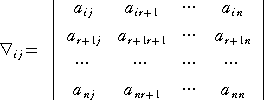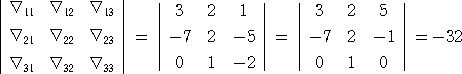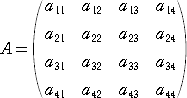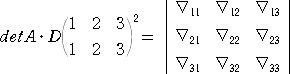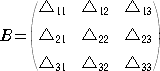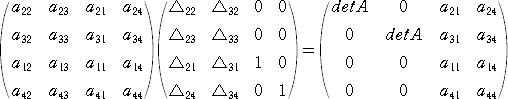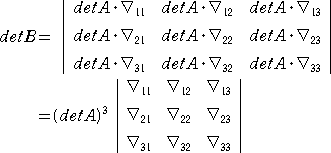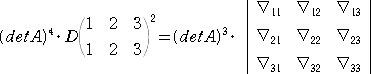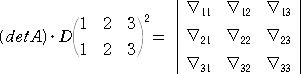ヤコビの定理 
平面上の3点 A( a , b ) 、B( c , d ) 、O( 0 , 0 ) で定まる
△ABO の面積 S は、
行列式を用いて
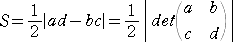
で与えられる。
面積や体積などの図形の計量以外にも、逆行列の計算や固有値の計算、変数変換の
ときのヤコビアン(関数行列式)の計算、空間での方程式の表現、2次曲面の分類など、
行列式の値を計算しなければならない場面は数多い。それだけ大切な計算ということで
ある。
しかし、次数が低い場合は、その計算は容易であるが、次数が高くなるにつれて、計算
量は膨大になる。
その計算を軽減するには、どのような方法があるのかを探求するのが、このページで
の目標である。
行列式の定義から、まず確認しておこう。
σを、n文字 1,2,3,・・・,n の置換として、ε(σ) をその符号とする。
もしも、σが偶置換ならば、ε(σ)=1であり、奇置換ならば、ε(σ)=−1である。
(置換についての説明は、こちらを参照)
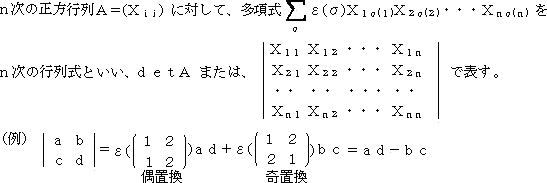
同様に

=aqz+brx+cpy−cqx−bpz−ary
4次以上の行列式も、定義に従って求められる。上記の2次と3次の場合を比較して分
かるように、その計算量は爆発的に増えていく。
( n!の変化と同じで、2!=2 、3!=6 、4!=24 、・・・。 普通に市販されている電卓では、も
はや、70!すら計算することができない。)
ところで、2次と3次の行列式の計算については、次のサラスの法則が有名である。こ
のおかげで、2次と3次の行列式の計算は、比較的容易である。
(2次の場合) (3次の場合)
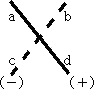
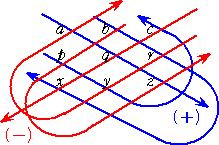
(少し見づらいかな?)
このサラスの法則は4次以上の行列式の計算には適用されない。従って、4次以上の場
合は、別の方策が必要である。
余因子の定義
n次の正方行列Aに対して、その第p行、第q列を取り去って得られる行列の行列式に
(−1)p+q を乗じたものを、行列A の第(p,q)余因子といい、△pqで表す。
(例) 実際に余因子を計算してみよう。
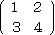
について、△11=(−1)2×4=4 、△12=(−1)3×3=−3
△21=(−1)3×2=−2 、△22=(−1)4×1=1
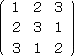
について、
△11=3・2−1・1=5 、 △12=−(2・2−3・1)=−1、
△13=2・1−3・3=−7 、△21=−(2・2−3・1)=−1、
△22=1・2−3・3=−7 、△23=−(1・1−2・3)=5、
△31=2・1−3・3=−7 、△32=−(1・1−2・3)=5、
△33=1・3−2・2=−1
4次以上の行列式の計算には、次の公式が大活躍である。
公式 n次の正方行列Aに対して、次が成り立つ。

(証明は、以下に示す行列式の性質の2.や3.などを用いて示される。)
この公式は、行列式の計算を1つの行に注目して展開するために用いられる。
例
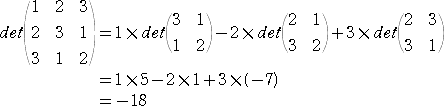
上記の例からも分かるように、n次の行列式を計算するには、(n−1)次の行列式を計算
すればよい。
同様の公式が、行と列を入れ替えたものについても成り立つ。
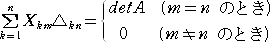
行列A の第(p,q)余因子 △pq から作られる余因子行列を A=(△pq) とおくと、
上記の公式は、
AtA=(detA)E tAA=(detA)E
であることを意味する。この関係で、上記公式を覚えておくといいだろう。
また、上記の公式は、ラプラス展開の特別な場合と見ることもできる。上記では、展開す
る行を第1行に指定しているが、これを複数行に分けて展開するのがラプラス展開である。
3次の正方行列の場合に限定して、ラプラス展開がどんなものかを見てみよう。
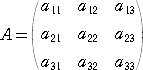
において、第1行と第2列、第3行と第3列を除外した小行列式は、通常
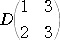
と表される。すなわち、
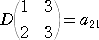
このとき、上記で除外していないところの第2行第1列を除外した小行列式は、
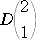
と表される。すなわち、
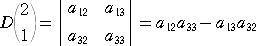
この小行列式を
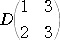
の補完小行列式(complementary minor)という。
| このとき、 |
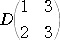 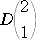 |
=a21(a12a33−a13a32) |
上記では、第1行と第3行と、行を固定して第2列と第3列を選んだ場合を考えたが、もち
ろん、列の選び方はこれ以外にもある。(全部で、3C2=3通りある!)
第1列と第2列を選んだ場合
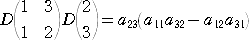
第1列と第3列を選んだ場合
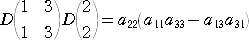
が成り立つ。ところで、
detA=a11a22a33+a12a23a31+a13a21a32−a13a22a31−a12a21a33−a11a23a32
=−a11a23a32+a12a23a31+a11a22a33−a13a22a31−a12a21a33+a13a21a32
=−a23(a11a32−a12a31)+a22(a11a33−a13a31)−a21(a12a33−a13a32)
となるので、


上式が、3次の正方行列 A
を、第1行、第3行を固定した場合のラプラス展開である。
和が、3つの列から2つの列を選び出すすべての場合について考えていることに注意する。
展開する行を1行だけに指定すると、チマチマした計算が延々と続く(十分規則的で単調な
作業である!)が、このラプラス展開だと、複数行に分けて展開できるので、多分計算は楽
になるはず?だが、実はそうでもないような...予感!
r
個の行を選んで指定すると、列の選び方は、nCr
通りある。この組み合わせの数だけ、
和を計算しなければならないので、もしかしたら、計算は思いの外大変なのかもしれない。
次の場合について、どちらが計算が楽なのか実証してみよう。
例 まずは、第1行に着目して、
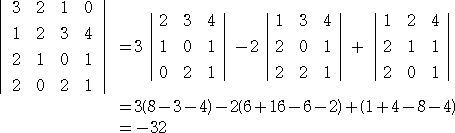
次に、第1行と第2行に着目してラプラス展開を行うと、
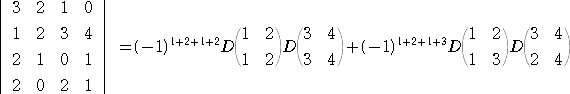
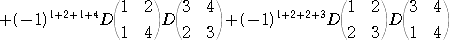
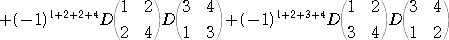
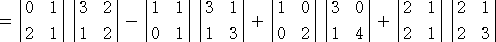
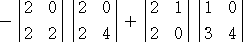
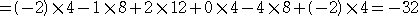
(コメント) 4次程度の行列式の計算に、ラプラス展開を使うのは何となく仰々しいような気
分かな?
上記のラプラス展開の計算例では、その意味合いが不十分であったが、次のような応用
例を見せられると、やはり「ラプラス展開」様々と言わざるを得ない。
2次の正方行列

において、 b または c が 0 だと当然、 detA=a・d が成り立つ。これと同様の性質が
n 次の正方行列においても成り立つ。
r 次の正方行列 A と n−r 次の正方行列 D について、
行列 B または 行列 C が零行列のとき、
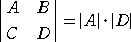
である。
(証明) B が零行列とする。第 r+1、r+2、・・・、n 行を固定した場合のラプラス展開に
おいて、
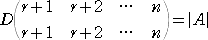
以外の行列式は、少なくとも1つの列がすべて 0 になるので、0 になる。
このときの補完的小行列式は、
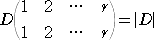
であり、かつ、
(−1)2(r+1+r+2+・・・+n)=1
なので、
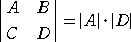
が成り立つ。 C が零行列でも同様である。 (証終)
さらに効率的に行列式を計算するために、次のような行列式の持つ性質が、よく利用され
る。
行列式の性質
1.行と列を入れかえても、行列式の値は不変(行と列に関して対称)
2.2つの行(列)を入れかえると、行列式の符号が変わる
3.行列式は、各行(列)に関して線形である
4.1つの行(列)の共通因数は、行列式の外にくくりだせる
5.1つの行(列)の要素が全て0ならば、行列式の値は0
6.2つの行(列)が比例するとき、行列式の値は0
7.1つの行(列)に任意の数をかけて、他の行(列)に加えても、行列式の値は不変
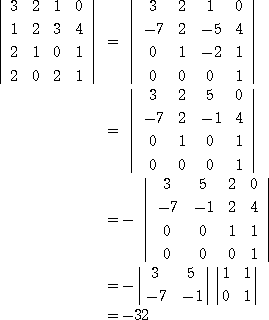
(計算例) 4次の行列式

上記の計算で、
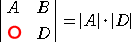
という公式を意識すると、次のようにも計算できる。
上記のような計算は、成分が数の場合は有効であるが、文字を含む場合には少し大変
かもしれない。
ところで、行列式の計算は、通常、正方行列が計算対象であるが、乗法が可能な場合に
計算対象をひろげてみると興味ある事実に遭遇する。
例えば、m×n
型の行列 A と n×m 型の行列 B の乗法 AB は可能で、m次の正方行
列となるが、
m>n のとき、 detAB=0
が常に成り立つ。
例
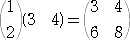
なので、その行列式は、 3×8−4×6=0 となる。
この、行列式が「0 」になるという現象は、全く偶発的なものではなく、当然起こるべくして
起こっていることである。
これは、次のように考えれば明かだろう。
たとえば、
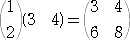
については、
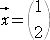
とおくと、
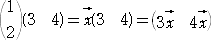
となり、2つの列が比例しているので、行列式の性質 6.から行列式は、0 となる。
一般には、
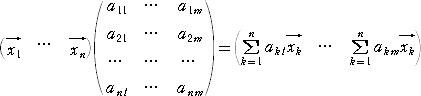
において、m>n より、行列式の性質の 3.を用いると、少なくとも2つの列が同じベクトル
になるので、行列式の性質 6.から行列式は、0 となる。
2次、3次の場合に比べて、4次以上になると、行列式の計算は非常に煩雑になる。そこ
で、次のヤコビの定理を紹介する。
ヤコビの定理(Jacobi) n次の正方行列 A =(aij) に対して、
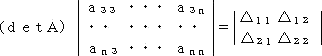
(右辺を式変形して、行列式の線形性を利用すれば、容易に示すことができる。詳しい
証明は、専門書に委ねる。)
また、上記で用いた記号を用いれば、ヤコビの定理は、
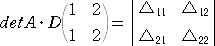
と書くこともできる。
ここでは、3次の正方行列 A=(aij) について確認しておこう。
右辺=△11△22−△12△21
=△21(−△12)+△22△11
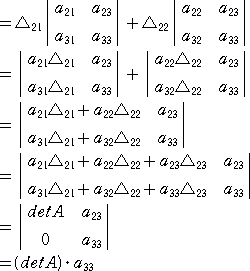
一般の場合の証明の骨子は上記と全く同様である。
また、
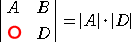
という公式を意識すると、次のような別証も可能だろう。
(別証) detA≠0 のとき、
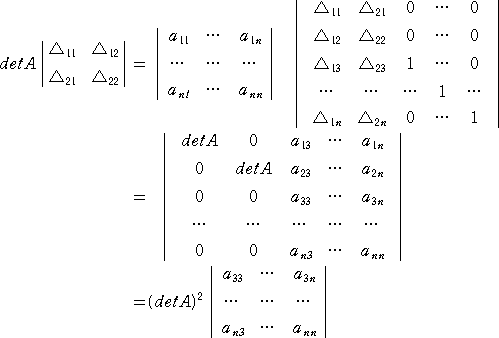
なので、
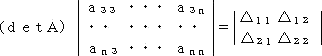
が成り立つ。
次に、detA=0 のときを考える。
いま、 aij=aij(0) であるような適当な連続関数 aij(x) をとり、
x≠0 のとき、 detA(x)≠0 ただし、 A(x)=(
aij(x) )
とする。このとき、先の議論から、
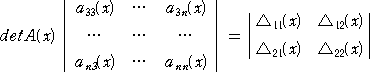
であるので、ここで、x → 0 とすると、やはり、detA=0 のときも
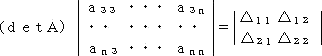
が成り立つ。 (別証終)
(補足) 上記の別証で、「 detA=0 」の場合が悩ましい。
関数の連続性を用いたものだが、ここは軽妙に次のように述べても許さ
れるところだろう。
行列 A の要素を全て異なる文字と考えると、 detA
は、これらの文字の
多項式で表され多項式として「 0 」ではない。よって、「 detA≠0 」としてよ
い。
(コメント) 上記の別証をみると、ヤコビの定理は、ごく自然な計算と感じられる!
(計算例)
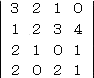 左の行列式の計算で、
左の行列式の計算で、
△11=1 、△12=−14 、△21=5 、△22=−6
| ヤコビの定理により、detA×(−2)= |
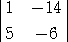 |
=64 |
なので、 detA=−32 |
(計算例)
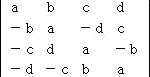 |
左の行列式の計算で、a2+b2+c2+d2=K とおくと、
△11=aK 、△12=bK 、△21=−bK 、△22=aK
|
なので、ヤコビの定理により、
(detA)(a2+b2)=(a2+b2)K2
ここで、 a2+b2=0 とすると、 a=b=0
このとき、 detA=c4+2c2d2+d4
よって、 detA=(a2+b2+c2+d2)2 が成り立つ。
また、 a2+b2≠0 とすると、
detA=K2=(a2+b2+c2+d2)2
以上から、何れにしても求める行列式の値は、
(a2+b2+c2+d2)2
となる。 |
上記の行列式の計算は、特殊すぎる場合で、次のような計算法が知られている。
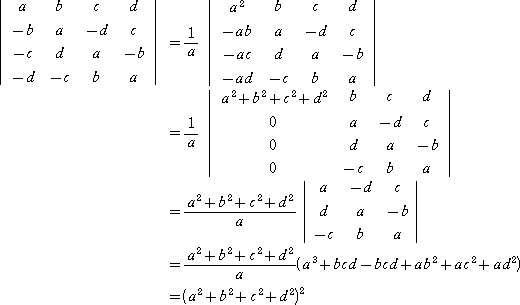
(コメント) 2つの計算を比較すると、ヤコビの定理のエレガントさがヒシヒシと伝わってき
ますね!
このヤコビの定理を一般化したものとして、シルベスターの定理(Sylvester)が知ら
れている。これらは、実は、次のよく知られた公式と密接に関係していることを最近気づか
された。
AtA=(detA)E より、 detA・dettA=(detA)n
よって、 detA=dettA=(detA)n-1 が成り立つ。
ただし、 A は、行列 A の余因子行列である。
ところで、ヤコビの定理は、
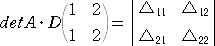
と書くことができたことを思いだそう。これが次のような形に一般化できることは十分予想さ
れる。
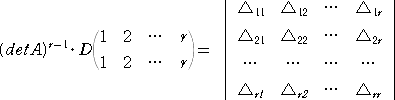
上式で、r=2 とすれば、ヤコビの定理が得られる。
また、 r=n のとき、
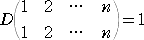
と考えれば、
detA=(detA)n-1
が得られる。
証明の骨子は、ヤコビの定理の別証と同様である。
(証明)
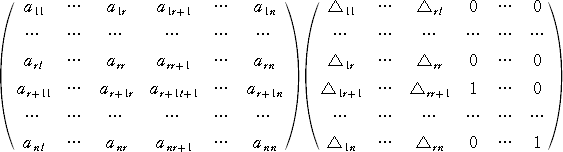
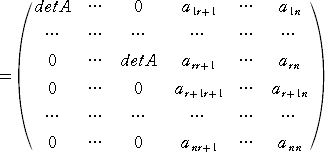
より、
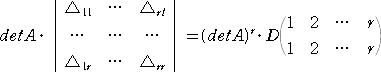
すなわち、
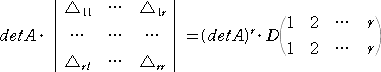
が成り立つ。上記で述べたように、detA≠0 としてよいので、
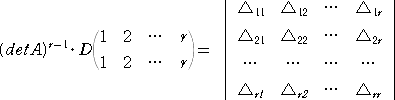
が成り立つ。 (証終)
上記の一般化は、ごく自然な形であったが、所謂「シルベスターの定理」と呼ばれるもの
は、この形とは違って、
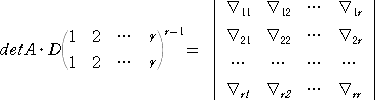
であることを主張するものである。
ただし、右辺の ∇ij は、行列 A の右下辺の n−r 次の正方行列に行列 A の第 i 行、
第 j 列を追加した行列の小行列式を表す。 すなわち、
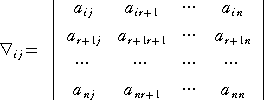
である。
ここで、r=2 のときは、正しくヤコビの定理そのものになることを確認しておこう。
上記の定義から、 ∇11=△22 、∇12=−△21 、∇21=−△12 、∇22=△11 なので、
∇11・∇22−∇12・∇21=△22・△11−(−△21)(−△12)=△11・△22−△12・△21
が成り立つ。
以上から、シルベスターの定理は、ヤコビの定理の一般化になっていると言える。
さて、本当にシルベスターの定理が成り立つのか、具体例でまず計算してみよう。
例
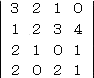 左の行列式において、
左の行列式において、
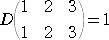
また、 ∇11=3・1−2・0=3 、 ∇12=2・1−0・0=2 、∇13=1・1−2・0=1
∇21=1・1−2・4=−7 、 ∇22=2・1−0・4=2 、∇23=3・1−2・4=−5
∇31=2・1−2・1=0 、 ∇32=1・1−0・1=1 、∇33=0・1−2・1=−2
よって、
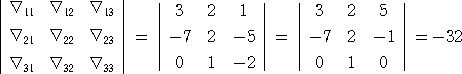
先の計算で、 detA=−32 であったので、シルベスターの定理の
左辺=(−32)・12=−32 、 右辺=−32
となり、シルベスターの定理は成り立っている。
さて、いよいよシルベスターの定理の証明に取りかかろう。
一般の場合を示すには少し煩雑になりそうなので、一般性を意識しつつ、n=4、r=3
の
場合についての略証で我慢することにしよう。多分、一般の場合も同様のはずである。
なお、この略証を試みるにあたり、上智大学理工学部物理学科 大槻東巳先生の講義
録を参考にさせていただいた。大槻先生に感謝いたします。
(略証) 行列
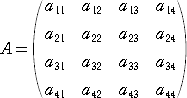
に対して、
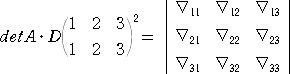
が成り立つことを占めせばよい。
ここで、
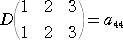
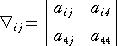
である。 いま、行列
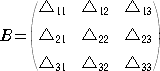
の第 i 行、第 j 列を取り除いた小行列式を、 Bij とおく。 例えば、
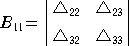
である。ヤコビの定理の別証と同様にして、
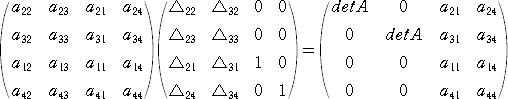
より、両辺の行列式をとる。行(列)を入れかえるとき、行列式の符号が変わるので、

行列式において、行と列を入れかえても行列式の符号は不変であるので、
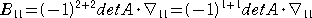
が成り立つ。同様にして、一般に、 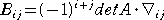 が成り立つ。
が成り立つ。
よって、行列 B の第( i , j )余因子は、
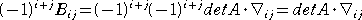
となる。行列 B の余因子行列を、Bで表すとすれば、
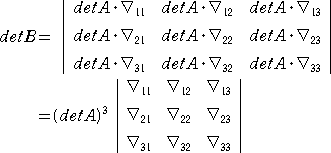
となる。
一方、 B・tB=(detB)E より、 det(B・tB)=(detB)3
すなわち、 detB・detB=(detB)3 より、 detB=(detB)2 が成り立つ。
ここで、
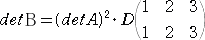
なので、
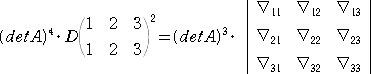
すなわち、
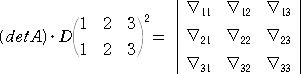
が成り立つ。 (証終)
(コメント) 大槻先生の証明がとても美しすぎて敷居が高く感じられたが、n=4、r=3 の
場合を考察することで、証明のテクニックや計算の進め方のコツ等がヒシヒシと
伝わってきて、ようやく五臓六腑に染み渡るような証明を得ることが出来た。
平成20年6月22日に当HPの掲示板「出会いの泉」にHN「文系大学生」様が
「ヤコビの定理・シルベスターの定理」に関する書き込みをされて以来、懸案であ
った証明が略証という形であるが完了した。
「文系大学生」様の書き込みに触発されて、6年ぶりに「ヤコビの定理」のペー
ジの見直しを行ったところ、いろいろ不備な点が散見されたので修正を行った。
また、シルベスターの定理は、当HPのレベルをはるかに越えるものとして、詳
細な記述をためらってきたが、ちょっと背伸びをすると手の届くレベルということ
が分かったので、いろいろとシルベスターの定理の周辺話題も含めて内容の補
充を行った。
以上の補充で、「文系大学生」様の疑問解消に役立ったのか、甚だ疑問である
が、取りあえず、当HPのレベルの範疇の中で、擱筆としたい。
(参考文献:佐武一郎 著 線形代数学(裳華房)
富永 晃 著 線形代数(聖文社)
三村征雄 著 代数学と幾何学(裳華房)
モストウ、サンプソン著 高野一夫訳 線形代数(マグロウヒル好学社)
石谷 茂 著 行列と行列式で楽しむ(現代数学社))

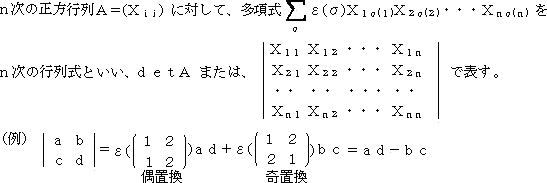

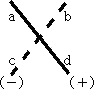

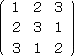
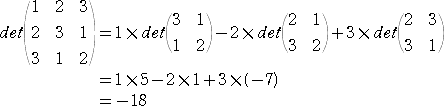
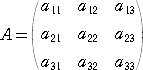

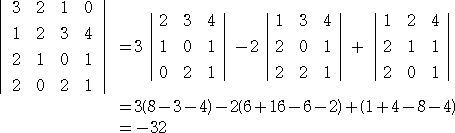
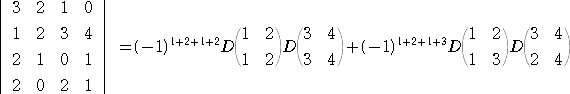


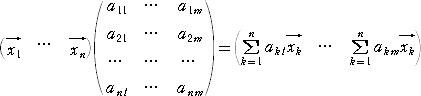
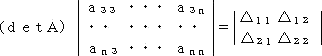
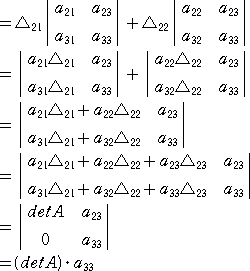
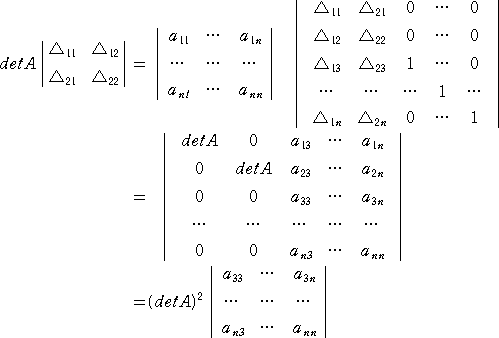
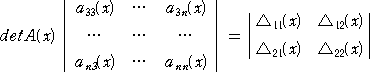
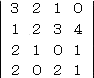 左の行列式の計算で、
左の行列式の計算で、