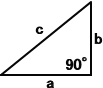
�@�@�@���p�O�p�`�ɂ����ẮA��2�{��2����2�@�����藧�B�i�O�����̒藝�j
�@�@�i���C���C���j���i�R�C�S�C�T�j�A�i�T�C�P�Q�C�P�R�j�A�i�V�C�Q�S�C�Q�T�j�A�E�E�E�Ȃǂ��A��
�@�@���m��ꂽ�s�^�S���X���ł���B
�@�@�@���̎��Ǝ����悤�Ȍ��ۂ��A���p�P�Q�O�x�̓݊p�O�p�`�ł��N����B
 |
�@�@�@���p�O�p�`�ɂ����ẮA��2�{��2����2�@�����藧�B�i�O�����̒藝�j �@�@�i���C���C���j���i�R�C�S�C�T�j�A�i�T�C�P�Q�C�P�R�j�A�i�V�C�Q�S�C�Q�T�j�A�E�E�E�Ȃǂ��A�� �@�@���m��ꂽ�s�^�S���X���ł���B �@�@�@���̎��Ǝ����悤�Ȍ��ۂ��A���p�P�Q�O�x�̓݊p�O�p�`�ł��N����B |
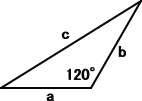 |
�@�@���}�ɂ����āA��2�{���E���{��2����2�@�����藧�B �@�@�i�ؖ��́A�]���藝���疾�炩�j �@�@�@�@�@�R2�{�R�E�T�{�T2���V2 �@�@�@�@�@�V2�{�V�E�W�{�W2���P�R2 �@�@�@�@�P�R2�{�P�R�E�R�T�{�R�T2���S�R2 �@�@�ȂǁA���������̔z�����ƁA�v�킸�������Ă��܂��B |
�@�U���@���A���̘b�����ʉ����ꂽ�B�i�����Q�R�N�W���W���t���j
��@���@��2�{���E���{��2����2�@�������R���̑g (���C���C��) �����߂�B
�����́A(���C���C��)��(�R�C�T�C�V)�A(�V�C�W�C�P�R)�A (�P�R�C�R�T�C�S�R)�A�E�E�E�@�Ȃ�
�i���j�@�u����ȃs�^�S���X���v�̂悤�ɁA�Q�������肳����B
�@�@�������|�P�A�������{�P�@�Ƃ���ƁA�^���́A�@�i���|�P�j2�{�i���|�P�j�i���{�P�j�{�i���{�P�j2����2
�@�@����āA�@��2���R��2�{�P�@���A�@��2�|�R��2���P�@���@�y�������� ��2�|�m�E��2���}�P
�@����������āA�@�i���C���j���i�Q�C�P�j�A�i�V�C�S�j�A�i�Q�U�C�P�T�j�A�i�X�V�C�T�U�j�A�E�E�E
�@���ꂩ��A(���C���C��)�����߂�ƁA
�i���C���j���i�V�C�S�j�@�̂Ƃ��A�@(���C���C��)��(�R�C�T�C�V)
�i���C���j���i�Q�U�C�P�T�j�@�̂Ƃ��A�@(���C���C��)��(�P�S�C�P�U�C�Q�U)�@���@(�V�C�W�C�P�R)
�i���C���j���i�X�V�C�T�U�j�@�̂Ƃ��A�@(���C���C��)��(�T�T�C�T�V�C�X�V)
�i���@�Q�l�F�u�ӂƊp�̔������W�U�v�A�u�s�^�S���X���̔����v�j
�@�e�m������A���̘b�����ʉ����ꂽ�B�i�����Q�R�N�W���W���t���j
�@�s�^�S���X���̏ꍇ(���u�s�^�S���X���̔����v�ɊT��������j�Ɠ��l�ɂ��āA��ʉ�������
�邱�Ƃ��قڂł���悤�ł��B
�@��2�{���E���{��2����2�@�E�E�E�i�P�j�@�̗��ӂ� ��2 �Ŋ����āA��/�������A��/������ �ƒu���ƁA
�@�@�@��2�{���E���{��2���P�@���(�Q)
�@�܂��A(�Q)�̗L�����������߂�B
�@�i�Q�j��̓_ (�|�P�C�O)��ʂ�X�� �� �̒��� �������i���{�P�j ��(�Q)�Ƃ̌�_�����߂�B
������āA�@��2�{���E���i���{�P�j�{��2�i���{�P�j2���P�@���A
�@�@�@�i��2�{���{�P�j��2�{�i�Q��2�{���j���{��2�|�P���O
�@���ꂪ�A�����|�P�����Ɏ����Ƃ͂킩���Ă���̂ŁA�����������āA
�@�@�@�i���{�P�j�o�i��2�{���{�P�j���{��2�|�P�p���O
����āA�����|�P�ȊO�̉��Ƃ��āA�@�����i�P�|��2�j/�i��2�{���{�P�j
�@���̂Ƃ��A�@�����i��2�{�Q���j/�i��2�{���{�P�j
�@����͂������(�Q)�̉��ŁA�� ��L�����ɂ���A���A�� ���L�����ɂȂ�B
�@�t�ɁA(�Q)�����L���� ���A�� �ɑ��āA�@������/�i���{�P�j�@�Ƃ����A���A��
�͏�L�̎��œ�
���邩��A���ׂĂ̗L�������͂��̂悤�ɂ��ē�����B
�@�������A(���C��)��(�|�P�C�O)�A(�|�P�C�|�Q)�͏����B
�@��� ���A�� �ɁA��2�{���{�P ��������ƁA���ꂼ��@�P�|��2�@�A��2�{�Q���@�ƂȂ�B
������ ���A���@�Ƃ��A������2�{���{�P�@�Ƃ����A���A���A�� �́A(�P)�����B
�@������/�� �Ƃ����āA���A���A�� �ɑ�����A������ ��2 �����������̂����߂� ���A���A�� �Ƃ���
�ƁA�@������2�|��2�@�A������2�{�Q�����@�A������2�{�����{��2�@�i�O���������j
�@�����́A(�P)�̎��R�����ł���B
�@���A�� ���������l�̂Ƃ��� ���A���A�� �́A���̂悤�ɂȂ�B
| �� | �� | �� | �� | �� | |
| �Q | �P | �R | �T | �V | |
| �R | �P | �W | �V | �P�R | |
| �R | �Q | �T | �P�U | �P�X | |
| �S | �P | �P�T | �X | �Q�P | �@���@�R�Ŋ���ƁA�@�T�@�R�@�V |
| �S | �R | �V | �R�R | �R�V |
�@��� �����S�A�����P �̂Ƃ��̂悤�ɁA���A�� ���݂��ɑf�ł����Ă� ���A���A��
����������
���Ƃ�����܂��B�s�^�S���X���̏ꍇ���������Ƃ͂����܂����A���A�� �̈���͋����Ƃ��邱��
�ɂ���ĉ���ł��܂��B
�@(A)�@���A�� �݂͌��ɑf�Ȑ����Ƃ���B
�@�@�@�@�@������2�|��2�@�A������2�{�Q�����@�A������2�{�����{��2
�@�@�@�̍ő���́A�P�܂��͂R�ł���B
�@����͐������ł��傤���B������������A�ǂ������ꍇ�� �P�A�R �ɂȂ邩���܂߂ďؖ�����
���������B�������Ȃ��Ȃ甽��������ĉ������B
�@�e�m����̑���ł��B�i�����Q�R�N�W���Q�T���t���j
�@�܂��A�u�f�� �� ���A���A�� �̌��ł���A�����R�v���ؖ�����B
�@������2�|��2���i���{���j�i���|���j�߂O�@�i�������@���j�@���A
�@�@�@�@���߂��@�i�������@���j�@�܂��́@���߁|���@�i�������@���j
�@������2�{�Q���������i���{�Q���j�߂O�@�i�������@���j�@���A
�@�@�@�@���߂O�@�i�������@���j�@�܂��́@���߁|�Q���@�i�������@���j
�@�\���͂S�ʂ肠�邪�A
�@�@�@���߂��@�i�������@���j�@�A���߁|�Q���@�i�������@���j
�̂Ƃ��ȊO�́A���߂���0�@�i�������@���j�ƂȂ薵���B
�@���߂��@�i�������@���j�@�A���߁|�Q���@�i�������@���j�̂Ƃ��́A�R����0�@�i�������@���j�ƂȂ邪�A
m��0�@�i�������@���j�̂Ƃ��͏�Ɠ��l�ɖ����B
�@����āA�����R�@�łȂ���Ȃ�Ȃ��B
���ɁA�u�X�́A���A�� �̌��ł͂Ȃ��v���ؖ�����B
�@�X���A���A�� �̌��ł���Ƃ���B�������A�R�́A���A�� �̌��ł���B
��̏ؖ��Ɠ��l�ɂ��āA�@���߂��@�i�������@�X�j�@�A���߁|�Q���@�i�������@�X�j�@�ŁA������A
�Rm��0�@�i�������@�X�j�@����A�@m��0�@�i�������@�R�j�@�����A�@m��n��0�@�i�������@�R�j�ƂȂ薵���B
�@�ȏ���A���A�� �̍ő���́A�P���R�ł���A�R�ɂȂ�̂́A
�@�@�@�@m��n�@�i�������@�R�j�ŁA��0�@�i�������@�R�j�ł͂Ȃ��Ƃ��B
���̂Ƃ��A������2�{�����{��2�߂R��2��0�@�i�������@�R�j�ł��邩��A���A���A�� �̍ő�����R
������A���A���A�� �̍ő���́A�P���R�ł���A�R�ɂȂ�̂́A
�@�@���|�����R�̔{���ł���Ƃ��i�������A���A���͂R�̔{���ł͂Ȃ����̂Ƃ���B�j
�@�ȏォ��A(A)�͍m��I�ɉ����܂����B������g���āA���Ƃ��Ƃ̖��ɑ�����͓����
�܂��B�������A���A���A�� �̍ő�����P�ł�����̂����ŏ\���ł��B
�@��2�{���E���{��2����2�@�������R���̑g(���C���C��)�ōő�����P�ł�����̂́A
�@�@�@������2�|��2�@�A������2�{�Q�����@�A������2�{�����{��2
�ŗ^������B
�@�������A���A���݂͌��ɑf�Ȏ��R���ŁA�������@���@���|���@�́A�R�̔{���łȂ��Ƃ���B
�@���܂łɎ��������Ƃł͂܂��s�\���ŁA���������ؖ����ׂ����Ƃ�����܂��B�����
��2�{���E���{��2����2�@�́A���A���Ɋւ��đΏ̂Ȃ̂ŁA(���C���C��)�����Ȃ�A(���C���C��)�����ł��B
��̎��͈�������\���܂���B
�@�Ⴆ�A(���C���C��)��(�R�C�T�C�V)�́A�����Q�A�����P�Ƃ��ē����܂����A(���C���C��)��(�T�C�R�C�V)
�͂��̌`�ł͓����܂���B
�@���̖��́A����������A�P�̊p���P�Q�O�x�ŁA�R�ӂ������ł���O�p�`�i�R�ӂ̍ő�
�����P�ł�����́j�����ׂċ��߂�Ƃ������̂ł��B
�@���������Ӗ��ł́A(�R�C�T�C�V)��(�T�C�R�C�V)�͓����O�p�`�Ȃ̂ň�������ł����ƌ����܂��B
�i�R�����g�j�@�U���@����A�e�m����A���̘b��̈�ʉ��Ɋ��ӂ��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@