丂摉俫俹偺乽晄摍幃偵梀傇乿偵偍偄偰丄僠僃價僔僃僼偺懡崁幃偑妶桇偟偨丅
乮俿倱們倛倕倐倷倱們倛倕倖倖 乮
丂偙偺儁乕僕偱偼丄偙偺懡崁幃偵偮偄偰偺偄傠偄傠側惈幙傪惍棟偟偨偄偲巚偆丅
丂僠僃價僔僃僼偺懡崁幃偵娭偡傞栤戣偼丄戝妛擖帋栤戣偵傕懡悢弌戣偝傟偰偄傞丅偪傚偆偳
崅峑俀擭惗偐傜戝妛弶擭媺偵偐偗偰偺夝愅妛偺堦偮偺柺敀偄榖戣側傫偩傠偆偲巚傢傟傞丅
丂埲壓偱丄値 偼帺慠悢偲偡傞丅
丂値 攞妏偺梋尫 們倧倱値兤 偼丄壛朄掕棟傪梡偄傞偲丄們倧倱兤丂偺懡崁幃偵側傞
丂偙偺偙偲偼偄偔偮偐偺幚尡傪偡傟偽娙扨偵梊憐偝傟傞丅
値亖侾丂偺偲偒丄丂們倧倱侾兤亖們倧倱兤
値亖俀丂偺偲偒丄丂們倧倱俀兤亖們倧倱2兤亅倱倝値2兤亖們倧倱2兤亅乮侾亅們倧倱2兤乯亖俀們倧倱2兤亅侾
値亖俁丂偺偲偒丄丂們倧倱俁兤亖們倧倱俀兤們倧倱兤亅倱倝値俀兤倱倝値兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮俀們倧倱2兤亅侾乯們倧倱兤亅俀倱倝値2兤們倧倱兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀們倧倱3兤亅們倧倱兤亅俀們倧倱兤亄俀們倧倱3兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖係們倧倱3兤亅俁們倧倱兤
値亖係丂偺偲偒丄丂們倧倱係兤亖俀們倧倱2俀兤亅侾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀乮俀們倧倱2兤亅侾乯2亅侾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俉們倧倱4兤亅俉們倧倱2兤亄侾
値亖俆丂偺偲偒丄
丂們倧倱俆兤亖們倧倱俁兤們倧倱俀兤亅倱倝値俁兤倱倝値俀兤
丂丂丂丂丂亖乮係們倧倱3兤亅俁們倧倱兤乯乮俀們倧倱2兤亅侾乯亅乮俁倱倝値兤亅係倱倝値3兤乯丒俀倱倝値兤們倧倱兤
丂丂丂丂丂亖俉們倧倱5兤亅侾侽們倧倱3兤亄俁們倧倱兤亅俀乮俁們倧倱兤亅係乮侾亅們倧倱2兤乯們倧倱兤乯乮侾亅們倧倱2兤乯
丂丂丂丂丂亖俉們倧倱5兤亅侾侽們倧倱3兤亄俁們倧倱兤亅俀乮係們倧倱3兤亅們倧倱兤乯乮侾亅們倧倱2兤乯
丂丂丂丂丂亖俉們倧倱5兤亅侾侽們倧倱3兤亄俁們倧倱兤亅俀乮係們倧倱3兤亅係們倧倱5兤亅們倧倱兤亄們倧倱3兤乯
丂丂丂丂丂亖侾俇們倧倱5兤亅俀侽們倧倱3兤亄俆們倧倱兤
丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂偙偺棳傟偱峴偔偲丄師偺栤戣偼梕堈偵夝寛偱偒傞偩傠偆丅
栤丂戣丂丂們倧倱乮兾/乮俀値乯乯丂偼戙悢揑悢偱偁傞偙偲傪帵偣丅
丂乮夝乯丂兤亖兾/乮俀値乯丂偲偍偔偲丄丂値兤亖兾/俀丂偱偁傞丅
丂丂丂丂偙偺偲偒丄丂們倧倱値兤 偼丄們倧倱兤丂偺懡崁幃偱昞偣傞偺偱丄
丂丂丂丂丂丂丂們倧倱値兤亖倎0們倧倱値兤亄倎1們倧倱値-1兤亄丒丒丒亄倎値-1們倧倱兤亄倎値亖侽
丂丂丂丂丂丂丂丂丂丂丂乮偨偩偟丄丂倎0丄倎1丄丒丒丒丄倎値-1丄倎値丂偼丄桳棟悢乯
丂丂丂丂傛偭偰丄們倧倱乮兾/乮俀値乯乯丂偼戙悢揑悢偱偁傞丅丂乮廔乯
乮僐儊儞僩乯丂們倧倱乮兾/係乯丄們倧倱乮兾/俉乯丄們倧倱乮兾/侾侽乯丄丒丒丒丂偼戙悢揑悢両
乮嶲峫乯丂師偺俫俹偵偍偄偰丄値攞妏偺岞幃乮俀亝値亝俀侽乯偑梌偊傜傟偰偄傞丅偦偺悢偵埑搢偝
丂丂丂丂傟傑偡丅
乮曗懌乯丂暯惉侾俋擭俉寧俀俇擔晅偗
丂宑滀媊弇戝妛棟岺妛晹偺暯惉侾俋擭搙擖帋栤戣偵庤崰側墳梡戣偑弌戣偝傟偨丅
乮侾乯丂cos俁兤亖俥乮cos兤乯 傪枮偨偡俁師幃 俥乮倶乯 偲丄cos係兤亖俧乮cos兤乯 傪枮偨偡係師幃
丂俧乮倶乯 傪媮傔傛丅
丂傑偨丄懡崁幃 俫乮倶乯 偱丄丂乮倶亅侾乯俫乮倶乯亖俧乮倶乯亅俥乮倶乯丂傪枮偨偡傕偺傪媮傔傛丅
乮俀乯丂侽亝兤亝兾丂偱偁傞偲偒丄丂俫乮cos兤乯亖侽 偱偁傞偨傔偵偼丄
丂丂兤亖cos乮俀兾/俈乯丂丄cos乮係兾/俈乯丂丄cos乮俇兾/俈乯丂
丂偱偁傞偙偲偑昁梫廫暘偱偁傞偙偲傪徹柧偣傛丅
乮俁乯丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯丂偺抣傪媮傔傛丅
丂偙偺栤戣偱偼丄cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯丂偺抣傪媮傔傞偙偲偑娽栚偲巚
傢傟傞丅乮侾乯乮俀乯偺摫擖傪梡偄偰夝偔偙偲傪媮傔偰偄傞偺偩傠偆丅
丂偙偙偵丄僠僃價僔僃僼偺懡崁幃偺怺墦偝傪姶偠傞偲偙傠偱偁傞丅
乮棯夝乯丂乮侾乯偵偮偄偰偼丄忋婰偺寁嶼偐傜丄
丂俥乮倶乯亖係倶3亅俁倶丂丄俧乮倶乯亖俉倶4亅俉倶2亄侾丂偱偁傞丅
丂傛偭偰丄丂俧乮倶乯亅俥乮倶乯亖俉倶4亅係倶3亅俉倶2亄俁倶亄侾丂傛傝丄
丂俧乮倶乯亅俥乮倶乯亖乮倶亅侾乯乮俉倶3亄係倶2亅係倶亅侾乯丂側偺偱丄俫乮倶乯亖俉倶3亄係倶2亅係倶亅侾
乮俀乯丂俫乮cos兤乯亖侽 偲偡傞偲丄丂俧乮cos兤乯亅俥乮cos兤乯亖侽丂偡側傢偪丄丂cos係兤亖cos俁兤
丂偙偺偲偒丄丂係兤亖俀値兾 亇 俁兤丂傛傝丄丂兤亖俀値兾丂丄俀値兾/俈丂乮値 偼惍悢乯
丂侽亝兤亝兾丂傪枮偨偡 兤 偼丄兤亖 侽 丄 俀兾/俈 丄 係兾/俈 丄俇兾/俈
丂偙偙偱丄丂兤亖 侽 偺偲偒丄丂俫乮侾乯亖俈亗侽丂側偺偱丄兤亖 侽 偼晄揔丅
傛偭偰丄丂兤亖 俀兾/俈 丄 係兾/俈 丄 俇兾/俈丂偑惉傝棫偮丅
丂媡偵丄兤亖 俀兾/俈 丄 係兾/俈 丄 俇兾/俈丂偑惉傝棫偮傕偺偲偡傞丅
丂偙偙偱丄丂椺偊偽丄丂兤亖 俀兾/俈丂偲偍偔偲丄
丂cos係兤亖cos乮俉兾/俈乯亖cos乮俀兾亅俇兾/俈乯亖cos乮俇兾/俈乯亖cos俁兤
丂偑惉傝棫偮丅懠偺応崌傕摨條偱偁傞丅
丂傛偭偰丄丂俧乮cos兤乯亅俥乮cos兤乯亖侽丂偑惉傝棫偮丅
丂偡側傢偪丄丂乮cos兤亅侾乯俫乮cos兤乯亖侽 丂偱偁傞偑丄
丂cos兤亗侾丂側偺偱丄丂俫乮cos兤乯亖侽 丂偑惉傝棫偮丅
乮俁乯丂乮俀乯傛傝丄丂cos乮俀兾/俈乯丄cos乮係兾/俈乯丄cos乮俇兾/俈乯丂偼丄
丂俁師曽掱幃丂俉倶3亄係倶2亅係倶亅侾亖侽丂偺堎側傞俁偮偺夝偱偁傞偺偱丄夝偲學悢偺娭學偐傜丄
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅係/俉亖亅侾/俀丂偲側傞丅丂乮廔乯
乮捛婰乯丂暯惉俀侾擭俁寧俁侾擔晅偗
丂忋婰偱偼丄cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅侾/俀丂偱偁傞偙偲傪帵偟偨偑丄嵍
曈偺暋嶨偝偵斾傋丄塃曈偺扨弮偝偵嬃偐傟傞曽傕懡偄偩傠偆丅
丂偙傟偼丄丂cos乮俀兾/俈乯丂丄cos乮係兾/俈乯丂丄cos乮俇兾/俈乯丂偑丄俁師曽掱幃
丂俉倶3亄係倶2亅係倶亅侾亖侽丂偺堎側傞俁偮偺夝偱偁傞偙偲偑媫強偱偁偭偨丅摨條偵偟偰丄
丂cos乮俀兾/俈乯cos乮係兾/俈乯cos乮俇兾/俈乯亖侾/俉
丂cos乮俀兾/俈乯cos乮係兾/俈乯cos乮俉兾/俈乯亖侾/俉
偲側傞偙偲傕懄摎偩傠偆丅偙偺傛偆偵鉟楉側抣偵側傞棟桼偼丄俧倎倢倧倝倱棟榑偐傜傕愢柧偝傟傞丅
乮捛婰乯丂暯惉俀侾擭係寧侾擔晅偗偱丄俽乮俫乯偝傫傛傝丄師偺傛偆側擖帋栤戣偑偁傞偙偲傪巉偭偨丅
搶嫗帨宐夛堛壢戝妛乮俀侽侽俉乯
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖倎
丂cos乮俀兾/俈乯cos乮係兾/俈乯cos乮俇兾/俈乯亖倐
偲偡傞丅 倎 丄 倐 偺抣傪媮傔偨偄丅埲壓偺愝栤(1)丄(2)丄(3)偵摎偊傛丅
(1)丂妏兤乮儔僕傾儞乯偑丂們倧倱俁兤亖們倧倱係兤丂傪傒偨偡偲偒丄夝偺傂偲偮偑們倧倱兤偱偁傞傛偆
丂側係師偺曽掱幃傪媮傔傛丅
(2)丂兤亖俀兾/俈丂偺偲偒丄們倧倱兤偑夝偺傂偲偮偱偁傞傛偆側俁師偺曽掱幃傪媮傔傛丅
(3)丂愝栤(2)偺寢壥傪梡偄偰丄倎 偍傛傃 倐 偺抣傪媮傔傛丅
丂宑滀媊弇戝妛偺侾擭屻偺弌戣偱偡偑丄栤偄偐偗偑尰栶崅峑惗岦偗偵峫偊傗偡偔岺晇偝傟
偰偄傑偡偹両
乮夝乯丂(1)丂攞妏偺岞幃傛傝丄丂係們倧倱3兤亅俁們倧倱兤亖俀們倧倱2俀兤亅侾
丂塃曈亖俀乮俀們倧倱2兤亅侾乯2亅侾亖俉們倧倱4兤亅俉們倧倱2兤亄侾丂側偺偱丄
丂俉們倧倱4兤亅俉們倧倱2兤亄侾亖係們倧倱3兤亅俁們倧倱兤
傛偭偰丄丂俉們倧倱4兤亅係們倧倱3兤亅俉們倧倱2兤亄俁們倧倱兤亄侾亖侽丂傛傝丄
丂媮傔傞係師曽掱幃偼丄丂俉倶4亅係倶3亅俉倶2亄俁倶亄侾亖侽
(2)丂(1) 傛傝丄丂乮倶亅侾乯乮俉倶3亄係倶2亅係倶亅侾乯亖侽
丂兤亖俀兾/俈丂偺偲偒丄丂們倧倱兤亗侾丂偱偁傞丅
傑偨丄丂們倧倱俁兤亖們倧倱乮俇兾/俈乯亖們倧倱乮兾亅兾/俈乯亖亅們倧倱乮兾/俈乯
丂們倧倱係兤亖們倧倱乮俉兾/俈乯亖們倧倱乮兾亄兾/俈乯亖亅們倧倱乮兾/俈乯丂傛傝丄丂們倧倱俁兤亖們倧倱係兤
偑惉傝棫偪丄們倧倱兤丂偼丄俁師曽掱幃偼丄俉倶3亄係倶2亅係倶亅侾亖侽丂偺夝偲側傞丅
(3)丂兤亖俀兾/俈丄係兾/俈丄俇兾/俈丂偼偡傋偰丂們倧倱俁兤亖們倧倱係兤丂傪傒偨偟丄
丂們倧倱乮俀兾/俈乯丄們倧倱乮係兾/俈乯丄們倧倱乮俇兾/俈乯丂偼憡堎側傞俁悢偱丄侾 偲偼堎側傞丅
傛偭偰丄俁悢偼丄(2) 偱摼傜傟偨俁師曽掱幃偺俁偮偺夝偲側傞丅夝偲學悢偺娭學偐傜丄
丂倎亖們倧倱乮俀兾/俈乯亄們倧倱乮係兾/俈乯亄們倧倱乮俇兾/俈乯亖亅侾/俀
丂倐亖們倧倱乮俀兾/俈乯們倧倱乮係兾/俈乯們倧倱乮俇兾/俈乯亖侾/俉丂丂丂乮廔乯
乮捛婰乯丂暯惉侾俋擭俋寧俀俋擔晅偗
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯丂偺抣傪媮傔傞偩偗偺栤戣偩偭偨傜丄師偺傛偆
偵夝偄偨曽偑憗摴偩傠偆丅
丂暋慺悢暯柺偵偍偄偰丄丂曽掱幃丂倅7亖侾丂偺夝偼壓恾偺傛偆偵暘晍偡傞丅
丂丂
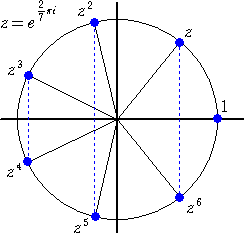
丂偙偺偲偒丄丂侾亄倸亄倸2亄倸3亄倸4亄倸5亄倸6亖侽丂偑惉傝棫偮丅
丂偙偙偱丄丂倸 偲 倸6丂丄丂倸2 偲 倸5丂丄丂倸3 偲 倸4丂偼屳偄偵嫟栶側暋慺悢側偺偱丄
丂倸 亄 倸6 亖 俀們倧倱乮俀兾/俈乯
丂倸2 亄 倸5 亖 俀們倧倱乮係兾/俈乯
丂倸3 亄 倸4 亖 俀們倧倱乮俇兾/俈乯
傛偭偰丄丂丂侾亄俀乮cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯乯亖侽丂傛傝丄
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅侾/俀
乮僐儊儞僩乯丂幚悢偺悽奅偱偳傫側偵柺搢側栤戣傕丄暋慺悢偺悽奅偱偼暯堈側栤戣偵惗傑傟曄
丂丂丂丂傢偭偰偟傑偄傑偡偹両
乮捛婰乯丂暯惉侾俋擭俋寧俁侽擔晅偗
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞 俙値倧値倷倣倧倳倱 偝傫偐傜偺忣曬偵傛傞偲師偺傛偆側暿夝
傕峫偊傜傟傞丅忋婰偱偼嫟栶暋慺悢傪梡偄偨偑丄埲壓偺夝偱偼丄弮悎偵曽掱幃傪夝偔偙偲偵
傛傝媮傔傜傟傞丅
丂兛亖倸亄倸2亄倸4丂乮丂偨偩偟丄 倸亖exp乮俀兾倝/俈乯丂乯丂偲偍偔偲丄
丂兛2亖倸2亄倸4亄倸8亄俀倸3亄俀倸6亄俀倸5亖倸2亄倸4亄倸亄俀倸3亄俀倸6亄俀倸5亖倸3亄倸6亄倸5亅侾
傛偭偰丄丂兛2亄兛亄侾亖倸亄倸2亄倸3亄倸4亄倸5亄倸6亖亅侾丂側偺偱丄兛 偼丄
俀師曽掱幃 倶2亄倶亄俀亖侽丂偺夝偲側傞丅夝偺岞幃偵傛傝丄
丂
丂偙偺偙偲偐傜丄丂暋慺悢 兛 偺幚悢晹傪斾妑偟偰丄
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俉兾/俈乯亖亅侾/俀
偲側傞丅丂偙偙偱丄丂cos乮俉兾/俈乯亖cos乮俇兾/俈乯丂側偺偱丄
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅侾/俀
偱偁傞丅
丂偝傜偵丄師偺傛偆側巃怴側夝朄傕峫偊傜傟傞傛偆偩丅傕偟偐偟偨傜丄偙偪傜偺夝朄偺曽偑丄傛傝
敪揥惈偺偁傞夝朄偐傕偟傟側偄丅
丂侾亄倸亄倸2亄倸3亄倸4亄倸5亄倸6亖侽丂偵偍偄偰丄丂倸亗侽丂側偺偱丄
丂侾/倸3亄侾/倸2亄侾/倸亄侾亄倸亄倸2亄倸3亖侽
丂乮倸亄侾/倸乯3亅俁乮倸亄侾/倸乯亄乮倸亄侾/倸乯2亅俀亄乮倸亄侾/倸乯亄侾亖侽
偡側傢偪丄丂乮倸亄侾/倸乯3亄乮倸亄侾/倸乯2亅俀乮倸亄侾/倸乯亅侾亖侽
傛偭偰丄丂兝亖倸亄侾/倸丂偲偍偔偲丄丂兝3亄兝2亅俀兝亅侾亖侽丂偲側傝丄
丂兝 偼丄俁師曽掱幃 倶3亄倶2亅俀倶亅侾亖侽丂偺夝偲側傞丅
偲偙傠偱丄丂兝亖倸亄侾/倸亖俀cos乮俀兾/俈乯丂偱丄
丂兝2亖乮倸亄侾/倸乯2亖倸2亄侾/倸2亄俀丂傛傝丄兝2亅俀亖倸2亄侾/倸2亖俀cos乮係兾/俈乯
偝傜偵丄丂乮兝2亅俀乯兝亖乮倸2亄侾/倸2乯乮倸亄侾/倸乯亖倸3亄侾/倸3亄倸亄侾/倸丂側偺偱丄
丂兝3亅俁兝亖倸3亄侾/倸3亖俀cos乮俇兾/俈乯
偙偺偲偒丄丂兝亄乮兝2亅俀乯亄乮兝3亅俁兝乯亖兝3亄兝2亅俀兝亅俀亖亅侾丂側偺偱丄
丂俀cos乮俀兾/俈乯亄俀cos乮係兾/俈乯亄俀cos乮俇兾/俈乯亖亅侾
偡側傢偪丄丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅侾/俀
乮僐儊儞僩乯丂摨偠栤戣偑丄偄傠偄傠側帇揰偐傜夝偐傟偰妝偟偄偱偡偹両偦傟偩偗宑滀媊弇戝妛
丂丂丂偺擖帋栤戣偼怺墦側傞椙栤偩偭偨偲偄偆偙偲偱偟傚偆偐丅
乮捛婰乯丂暯惉俀係擭俈寧侾俁擔晅偗偱丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偑
丂cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯
偵偮偄偰丄暿夝傪峫偊傜傟偨丅
乮夝乯丂榓傪愊偵側偍偡岞幃傛傝丄
丂cos(2兾/7)亄cos(6兾/7)亖2cos((6兾/7)亄(2兾/7))/2丒cos((6兾/7)-(2兾/7))/2
亖2cos(4兾/7)cos(2兾/7)
偵傛傝丄梌幃亖2cos(4兾/7)cos(2兾/7)亄cos(4兾/7)亖cos(4兾/7){2cos(2兾/7)亄1}丒丒丒仚
丂cos(2兾/7)亖1-2sin2(兾/7)丂傛傝丄2cos(2兾/7)亄1亖3-4sin2(兾/7)丂側偺偱丄
丂仚亖cos(4兾/7){3-4sin2(兾/7)}丒丒丒仛
偙偙偱丄{}撪偺幃偵婥偑偮偔偲丄仛偺幃偼
仛亖cos(4兾/7){(sin(兾/7))(3-4sin2(兾/7)}/sin(兾/7)
丂亖cos(4兾/7){3sin(兾/7)-4sin3(兾/7)}/sin(兾/7)亖cos(4兾/7)sin(3兾/7)/sin(兾/7)丒丒丒丒丒仛仛
丂偙偙偱丄cos(4兾/7)sin(3兾/7)亖(1/2){sin((4兾/7)亄(3兾/7))-sin((4兾/7)-(3兾/7))}
丂丂亖(1/2){sin兾-sin(兾/7)}亖-(1/2)sin(兾/7)
傛偭偰丄仛仛亖-(1/2)sin(兾/7)/sin(兾/7)亖-1/2
埲忋偐傜丄cos乮俀兾/俈乯亄cos乮係兾/俈乯亄cos乮俇兾/俈乯亖亅侾/俀丂丂乮廔乯
丂堦斒偵丄們倧倱値兤 傪丄壛朄掕棟傪梡偄偰揥奐偟偨幃偵偍偄偰丄們倧倱兤亖倃丂偲偟偰摼傜傟傞
懡崁幃傪丄僠僃價僔僃僼偺懡崁幃偲偄偆丅捠忢丄俿値乮倃乯丂偱昞偝傟傞丅
丂丂偡側傢偪丄丂丂們倧倱値兤亖俿値乮們倧倱兤乯丂偱偁傞丅
丂忋婰偺寁嶼偐傜丄
丂俿1乮倃乯亖倃
丂俿2乮倃乯亖俀倃2亅侾
丂俿3乮倃乯亖係倃3亅俁倃
丂俿4乮倃乯亖俉倃4亅俉倃2亄侾
丂俿5乮倃乯亖侾俇倃5亅俀侽倃3亄俆倃
偱偁傞偙偲偑暘偐傞丅
丂偝偰丄忋婰偺娭悢幃傪尒偰丄俿値乮倃乯 偼丄値 師偺懡崁幃偱丄嵟崅師偺崁偺學悢偼丄俀値-1
偱偁傞偙偲偑梊憐偝傟傞丅丂偙偺偙偲傪妋擣偟偰傒傛偆丅
丂僪丒儌傾僽儖偺岞幃偵傛傝丄倝 傪嫊悢扨埵偲偟偰丄們倧倱(値兤)亄倝丒倱倝値(値兤)亖乮們倧倱兤亄倝丒倱倝値兤乯値
塃曈偵懳偟偰丄俀崁掕棟傪梡偄偰揥奐偡傞偲丄
丂
偲側傞偺偱丄椉曈偺幚晹傪斾妑偡傟偽丄
丂
偲側傞丅乮忋偺幃偱丄乵倶乶 偼丄僈僂僗婰崋偱偁傞丅乯
丂傛偭偰丄偙偺幃偵偍偄偰丄們倧倱兤亖倃丂偲偡傞偲丄俿値乮倃乯 偼丄値 師偺懡崁幃偵側傞偙偲偑暘
偐傞丅
丂偝傜偵丄嵟崅師偺崁偺學悢偼丄弴楍丒慻崌偣偺棟榑乮仺丂嶲峫丗僷僗僇儖偺嶰妏宍乯偐傜丄
丂値俠0亄値俠2亄値俠4亄丒丒丒丒丒丂亖俀値-1
偱偁傞丅
丂傑偨丄掕悢崁偵偮偄偰傕丄師偺帠幚偑惉傝棫偮丅
丂値佭侽丂乮倣倧倓丂係乯丂偺偲偒丄丂掕悢崁亖侾
丂値佭侾丂乮倣倧倓丂係乯丂偺偲偒丄丂掕悢崁亖侽
丂値佭俀丂乮倣倧倓丂係乯丂偺偲偒丄丂掕悢崁亖亅侾
丂値佭俁丂乮倣倧倓丂係乯丂偺偲偒丄丂掕悢崁亖侽
丂徹柧偼丄忋婰偺丂們倧倱(値兤)丂偺幃偐傜柧傜偐偱偁傠偆丅
丂僠僃價僔僃僼偺懡崁幃傪埖偆応崌偺拲堄揰偼丄們倧倱兤亖倃丂偲抲偄偰偄傞娭學偐傜丄
丂丂丂丂丂丂丂丂丂亅侾 亝 倃 亝 侾
偱偁傞偙偲偩傠偆丅
丂偙偺偲偒丄奺帺慠悢 値 偵懳偟偰丄娭悢 俿値乮倃乯 偺僌儔僼傪昤偔偲丄僠僃價僔僃僼偺懡崁幃偺
摿挜偑晜偐傃忋偑偭偰偔傞丅
丂丂
 丂丂丂丂
丂丂丂丂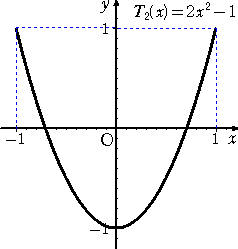
丂丂
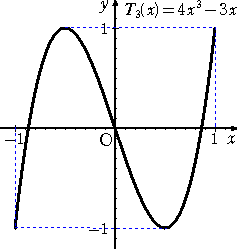 丂丂丂丂
丂丂丂丂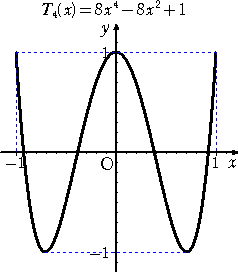
丂丂
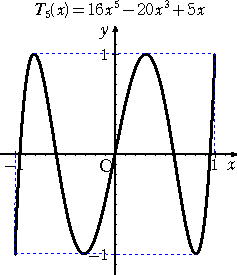
丂埲忋偺俆偮偺僌儔僼偐傜暘偐傞傛偆偵丄壗傟傕丄抣堟偼丄丂亅侾 亝 倄 亝 侾丂偱偁傞丅
傕偭偲傕丄偙傟偼丄們倧倱値兤亖俿値乮們倧倱兤乯丂偐傜柧傜偐偱偁傠偆丅
丂傑偨丄娭悢 俿値乮倃乯 偺僌儔僼傪挱傔偰偄傞偲丄嬌戝抣偲嬌彫抣偑岎屳偵尰傟偰偄傞丅偙偺揰
傕僠僃價僔僃僼偺懡崁幃偺摿挜側偺偩傠偆丅
丂偝傜偵丄亅侾 亝 倃 亝 侾丂偺斖埻偱丄曽掱幃丂俿値乮倃乯亖侽丂偼丄堎側傞 値 屄偺幚悢夝傪帩
偮偙偲傕暘偐傞丅
丂幚嵺偵丄曽掱幃丂俿値乮倃乯亖侽丂偲側傞 倃亖們倧倱兤 偼丄們倧倱(値兤)亖侽 傪枮偨偡 兤 偵傛偭偰媮
傔傜傟傞丅偙偺嶰妏曽掱幃偺堦斒夝偼丄
丂値兤亖倠兾亅乮侾/俀乯兾丂丂乮 倠 偼丄惍悢乯
側偺偱丄兤亖乮俀倠亅侾乯兾/俀値丂丂乮 倠 偼丄惍悢乯丂偲側傞丅
丂們倧倱兤 偼丄嬼娭悢偱偁傞偺偱丄憡堎側傞 們倧倱兤 偺抣傪梌偊傞傕偺偲偟偰偼丄
倠亖侾丄俀丄俁丄丒丒丒丄値 傪戙擖偟偰丄
丂兤1亖兾/俀値丂丄兤2亖俁兾/俀値丂丄兤3亖俆兾/俀値丂丄丒丒丒丄兤n亖乮俀値亅侾乯兾/俀値
偺 値 屄懚嵼偡傞丅偙傟傜偑丄曽掱幃丂俿値乮倃乯亖侽丂偺幚悢夝 倃値亖們倧倱兤値 傪梌偊傞丅
乮僐儊儞僩丗 曽掱幃丂俿値乮倃乯亖侽丂偑昁偢堎側傞 値 屄偺幚悢夝傪帩偮側傫偰丄偲偰傕惈幙乮惈奿丠乯偑偄偄偱偡偹両乯
丂偲偙傠偱丄 們倧倱値兤 偵偍偄偰丄們倧倱兤亖倃丂偲偟偰僠僃價僔僃僼偺懡崁幃偑摼傜傟偨偑丄
倱倝値値兤 偵偮偄偰傕摨條偺偙偲偼偱偒側偄偺偱偁傠偆偐丠
丂幚偼丄懡彮旤偟偝偵偼寚偗傞偑丄摨庬偺懡崁幃偼偱偒傞傛偆偩丅
丂僪丒儌傾僽儖偺岞幃偵傛傝丄倝 傪嫊悢扨埵偲偟偰丄
丂們倧倱(値兤)亄倝丒倱倝値(値兤)亖乮們倧倱兤亄倝丒倱倝値兤乯値
塃曈偵懳偟偰丄俀崁掕棟傪梡偄偰揥奐偡傞偲丄
丂
偲側傞偺偱丄椉曈偺嫊晹傪斾妑偡傟偽丄
丂
偲側傞丅乮忋偺幃偱丄乵倶乶 偼丄僈僂僗婰崋偱偁傞丅乯
丂倱倝値2兤亖侾亅們倧倱2兤 側偺偱丄
丂
丂傛偭偰丄
丂
偲偍偔偲丄倱倝値乮値兤乯亖俽値乮們倧倱兤乯丒倱倝値兤丂傪枮偨偡懡崁幃 俽値乮倃乯 偑懚嵼偡傞丅
丂偨偲偊偽丄丂倱倝値俀兤亖俀們倧倱兤丒倱倝値兤丂傛傝丄丂俽2乮倃乯亖俀倃
倱倝値俁兤亖俁倱倝値兤亅係倱倝値3兤亖乮俁亅係倱倝値2兤乯丒倱倝値兤亖乮俁亅係乮侾亅們倧倱2兤乯乯丒倱倝値兤
亖乮係們倧倱2兤亅侾乯丒倱倝値兤
傛傝丄丂俽3乮倃乯亖係倃2亅侾
倱倝値係兤亖俀倱倝値俀兤們倧倱俀兤亖係倱倝値兤們倧倱兤乮俀們倧倱2兤亅侾乯亖乮俉們倧倱3兤亅係們倧倱兤乯丒倱倝値兤
傛傝丄丂俽4乮倃乯亖俉倃3亅係倃
偲側傞丅丂傕偪傠傫丄丂俽1乮倃乯亖侾丂偱偁傞丅
丂仸丂俵倎倲倛倕倣倎倲倝們倎丂偵偍偄偰偼丄倱倝値乮値亄侾乯兤亖俽値乮們倧倱兤乯丒倱倝値兤丂偲掕媊偝傟傞傜偟偄丅
丂俽値乮倃乯 偺掕媊偼丄偍悽帿偵傕旤偟偄偲偼尵偊側偄偑丄懡崁幃 俿値乮倃乯 偲 俽値乮倃乯 偵偼丄
幚偼丄怺墦側傞娭學偑惉棫偡傞丅
丂俿1乮倃乯亖倃丂丂丂丂丂丂丂丂丂丂丂丂俽1乮倃乯亖侾
丂俿2乮倃乯亖俀倃2亅侾丂丂丂丂丂丂丂丂俽2乮倃乯亖俀倃
丂俿3乮倃乯亖係倃3亅俁倃丂丂丂丂丂丂丂俽3乮倃乯亖係倃2亅侾
丂俿4乮倃乯亖俉倃4亅俉倃2亄侾丂丂丂丂俽4乮倃乯亖俉倃3亅係倃
丂忋婰偺寁嶼寢壥偐傜丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俿値乮倃乯乯乫亖値丒俽値乮倃乯
偲偄偆娭學幃偺惉傝棫偮偙偲偑梊憐偝傟傞丅乮偙偙偱丄嵍曈偺乮丂乯乫偼丄摫娭悢傪昞偡丅乯
丂傕偭偲傕丄偙傟偼師偺旝暘偺寁嶼偐傜柧傜偐偱偁傠偆丅
丂們倧倱値兤亖俿値乮們倧倱兤乯丂偺椉曈傪丄兤 偱旝暘偡傟偽丄
丂亅値丒倱倝値値兤亖乮俿値乮們倧倱兤乯乯乫丒乮亅倱倝値兤乯
丂偙偙偱丄丂倱倝値値兤亖俽値乮們倧倱兤乯丒倱倝値兤丂側偺偱丄
丂乮俿値乮們倧倱兤乯乯乫亖値丒俽値乮們倧倱兤乯丂偡側傢偪丄懡崁幃偲偟偰丄
丂丂乮俿値乮倃乯乯乫亖値丒俽値乮倃乯
丂偑惉傝棫偮丅
丂傑偨丄俿値乮倃乯丄俽値乮倃乯偼嫟偵摨偠慟壔幃丂丂倎値亄2亅俀丒倃丒倎値亄1亄倎値亖侽
傪枮偨偡偲偄偆帠幚傕柺敀偄丅
丂幚嵺偵丄丂乮們倧倱兤亄倝丒倱倝値兤乯値亄1亖乮們倧倱兤亄倝丒倱倝値兤乯丒乮們倧倱兤亄倝丒倱倝値兤乯値丂偵偍偄偰丄
丂們倧倱乮値亄侾乯兤亄倝丒倱倝値乮値亄侾乯兤亖乮們倧倱兤亄倝丒倱倝値兤乯丒乮們倧倱値兤亄倝丒倱倝値値兤乯
側偺偱丄丂丂俿値亄1亄倝丒俽値亄1丒倱倝値兤亖乮們倧倱兤亄倝丒倱倝値兤乯丒乮俿値亄倝丒俽値丒倱倝値兤乯
丂幚晹偲嫊晹傪斾妑偟偰丄
丂俿値亄1亖俿値丒們倧倱兤亅俽値丒倱倝値2兤亖俿値丒們倧倱兤亅俽値丒乮侾亅們倧倱2兤乯
亖俽値丒們倧倱2兤亄俿値丒們倧倱兤亅俽値
偡側傢偪丄丂俿値亄1亖俽値丒倃2亄俿値丒倃亅俽値
丂傑偨丄丂俽値亄1亖俽値丒們倧倱兤亄俿値
偡側傢偪丄丂俽値亄1亖俽値丒倃亄俿値
偑惉傝棫偮丅
丂俿値亖俽値亄1亅俽値丒倃丂傪戞侾幃偵戙擖偟偰丄
丂丂俽値亄2亅俽値亄1丒倃亖俽値丒倃2亄乮俽値亄1亅俽値丒倃乯丒倃亅俽値
偙傟傛傝丄丂俽値亄2亅俀俽値亄1丒倃亄俽値亖侽丂丂偑惉傝棫偪丄俽値 偼丄
慟壔幃丂倎値亄2亅俀丒倃丒倎値亄1亄倎値亖侽丂傪枮偨偡偙偲偑帵偝傟偨丅
丂摨條偵丄
俿値亄2亅俀俿値亄1丒倃亄俿値
亖俽値亄1丒倃2亄乮俽値亄2亅俽値亄1丒倃乯丒倃亅俽値亄1亅俀乮俽値亄2亅俽値亄1丒倃乯丒倃亄俽値亄1亅俽値丒倃
亖亅乮俽値亄2亅俀俽値亄1丒倃亄俽値乯丒倃
亖侽
丂傛偭偰丄俿値 傕丄慟壔幃丂倎値亄2亅俀倃丒倎値亄1亄倎値亖侽丂傪枮偨偡偙偲偑帵偝傟偨丅
乮曗懌乯丂暯惉侾俉擭侾俀寧俀侽擔晅偗
丂偙偺儁乕僕偼丄暯惉侾俈擭侾寧侾侾擔晅偗偱傾僢僾偝傟偨偑丄崱撉傒曉偟偰傒傞偲丄寁嶼偺抰
愘偝偑栚棫偮丅
丂俿値乮倃乯丂偑丄 慟壔幃丂倎値亄2亅俀丒倃丒倎値亄1亄倎値亖侽丂傪枮偨偡偙偲傪帵偡偲偒丄忋婰偺傛偆
偵埲慜寁嶼偟偨偑丄師偺傛偆偵寁嶼偟偨曽偑娙扨偩傠偆丅
丂忋婰傛傝丂丂俽値亄2亅俀俽値亄1丒倃亄俽値亖侽
傛偭偰丄丂俽値亄3亅俀俽値亄2丒倃亄俽値亄1亖侽
傑偨丄丂丂倃俽値亄2亅俀俽値亄1丒倃2亄倃俽値亖侽丂側偺偱丄俀幃傪曈乆堷偄偰丄
丂乮俽値亄3亅倃俽値亄2乯亅俀倃乮俽値亄2亅倃俽値亄1乯亄俽値亄1亅倃俽値亖侽
偙偙偱丄丂俿値亖俽値亄1亅倃俽値丂側偺偱丄 俿値亄2亅俀倃俿値亄1亄俿値亖侽
偲側傝丄丂俿値 傕丄慟壔幃丂倎値亄2亅俀倃丒倎値亄1亄倎値亖侽丂傪枮偨偡丅
乮暿夝乯丂俿値亄2亅俀倃俿値亄1亄俿値亖侽丂偺椉曈傪旝暘偟偰傕娙扨側寁嶼偐傜丄
丂値乮俽値亄2亅俀俽値亄1丒倃亄俽値乯亖侽丂偡側傢偪丂俽値亄2亅俀俽値亄1丒倃亄俽値亖侽
傪帵偡偙偲偑偱偒傞丅
乮僐儊儞僩丗 慡偔堎側傞懡崁幃丂俿値 偲 俽値 摨巑偑丄慡偔摨偠慟壔幃傪枮偨偡側傫偰晄巚媍偱偡偹両傕偪傠傫乽晄巚
丂丂丂丂丂丂媍乿偲偼丄媈栤偺堄枴偱偼側偔偰姶扱偺堄枴偱偡丏丏丏丅偁傞曽偼乽摉慠乿偲尵傢傟傑偡偑丏丏丏両乯
乮捛婰乯丂暯惉俀侽擭俉寧侾係擔晅偗
丂忋婰偱偼丄俿値 偑慟壔幃 俿値亄2亅俀倃俿値亄1亄俿値亖侽丂傪枮偨偡偙偲傪帵偡偺偵丄俽値 傪妶梡
偡傞偲偄偆忣偗側偄夝朄乮傑乣惉傝峴偒忋偟傚偆偑側偄偲尵偊偽偟傚偆偑側偄偑丏丏丏乯偵側偭偰偄
傞偑丄傕偪傠傫捈愙揑偵帵偡偙偲傕壜擻偱偁傞丅
俿値亄2亅俀倃俿値亄1亄俿値亖們倧倱乮値亄俀乯兤亅俀們倧倱兤們倧倱乮値亄侾乯兤亄們倧倱値兤
亖乷們倧倱乮値亄俀乯兤亄們倧倱値兤乸亅俀們倧倱兤們倧倱乮値亄侾乯兤
亖俀們倧倱乮値亄侾乯兤們倧倱兤亅俀們倧倱兤們倧倱乮値亄侾乯兤亖侽
丂偙偺慟壔幃傪梡偄傞偲丄師偺帠幚偑梕堈偵帵偝傟傞丅
丂慡偰偺帺慠悢 値 偵懳偟偰丄丂俿値丂偼桳棟學悢偺 値 師偺懡崁幃偱偁傞
乮徹柧乯丂丂俿1乮倃乯亖倃丂丄丂俿2乮倃乯亖俀倃2亅侾丂傛傝丄柧傜偐偵柦戣偼丄値亖侾丄値亖俀丂偺偲偒偵
丂惉傝棫偮丅
値亖倠丄値亖倠亄侾丂乮倠亞侾偺擟堄偺帺慠悢乯偺偲偒丄柦戣偑惉傝棫偮偲壖掕偡傞丅丂偡側傢偪丄
俿倠亄1丂丄俿倠丂偼丄偦傟偧傟桳棟學悢偺 倠亄侾師丄倠師偺懡崁幃偱偁傞丅
偙偺偲偒丄丂俿倠亄2亖俀倃俿倠亄1亅俿倠丂傛傝丄丂俿倠亄2 偼丄桳棟學悢偺 倠亄俀師偺懡崁幃偲側傞丅
丂傛偭偰丄柦戣偼丄値亖倠亄俀丂偺偲偒傕惉傝棫偮丅
偟偨偑偭偰丄慡偰偺帺慠悢 値 偵懳偟偰丄俿値丂偼桳棟學悢偺 値 師偺懡崁幃偱偁傞丅丂乮徹廔乯
丂偙偺寢壥傪梡偄傞椺戣偲偟偰偼丄師偺栤戣偑偁偘傜傟傞丅