
曲線の概形を思い通りに描けるようになったのは、私の場合、高校3年生の頃であろう
か。微分という武器を用いて、種々の曲線の概形を描くことは密かな楽しみでもあった。
ただ、全てが手計算によるものなので、あまり複雑なものを描くことはできなかった。
昨今の描画ソフトの進歩は著しい。関数式さえ分かれば、あんなものも、こんなものもとい
うくらいに鮮やかに描いてくれる。
このページでは、昔出来なかったことを描画ソフトを武器として、いろいろな曲線の概形に
挑戦したいと思う。
標準的な曲線の概形については、当HPの中の「いろいろな曲線」にまとめられている。
また、これから描かれる曲線の方程式には、ガウスの記号やら絶対値やらが複雑に絡
み合ってくる。その結果として、思いもかけない美しい曲線の概形が出現するわけで、ほと
んど感動的な出会いになると思う。
例 (x−[ x+1/2 ])2+(y−[ y+1/2 ])2=1/16
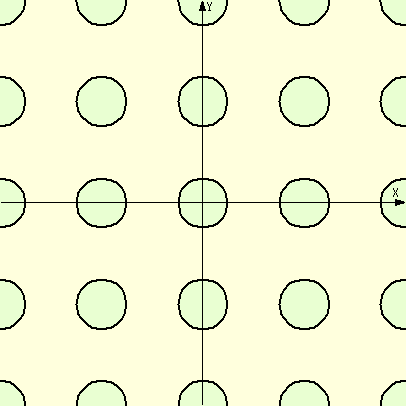
(コメント) たった一つの関数式で、平面上無限に広がる円が描けるわけで、「これはスゴ
イ!」と思いました。こんなことに感動できる感性を大切にしたいですね!
例 (x−[ x+1/2 ])2+(y−[ y+1/2 ])2=5/16
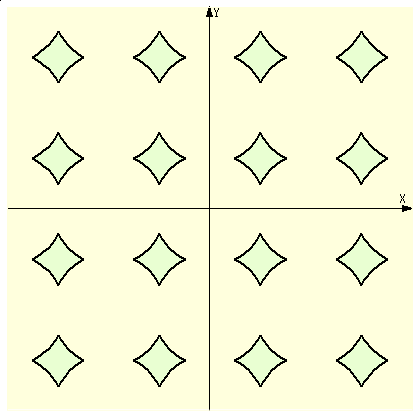
(コメント) 右辺の数字が、1/16 から5/16 に変わっただけなのに模様がガラリと様変わ
りですね!でも、じっと見つめていると、やはり無数の円が...。
例 (x−2|x|/x)2+(y−2|y|/y)2=5
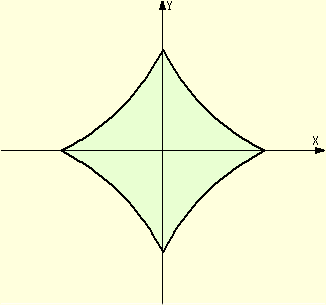
(コメント) 式は絶対値を使って込みいっているのに、出来る図形は単純!できれい。
この形は星芒形に似ているが、関係はなさそう...?
例 y4−x4−4y2+9x2=0
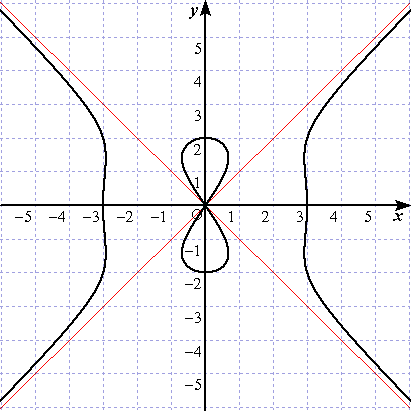
(コメント) この曲線は、悪魔の曲線と言われるそうだ。(何でだろう?)
x2 や y2 の係数をいろいろ変えてみると結構面白い!
(追記) 平成21年9月4日付け
上図ではグラフ描画ソフトを用いたので、うっかり漸近線が存在することを忘れてしまった。
このことを、広島工業大学の大川研究室よりご指摘いただいた。大川研究室に感謝します。
上記の曲線は、漸近線として、 y=±x を持つ。
実際に、 y4−x4−4y2+9x2=0 より、(y/x)4−1−4(y/x)2・(1/x)2+9/x2=0
よって、 x → ±∞ のとき、 y/x → ±1
さらに、分子の有理化を2回行うことにより、
x → ±∞ のとき、 y±x → 0 であることが分かる。
よって、曲線 y4−x4−4y2+9x2=0 は、漸近線 y=±x を持つ。 (終)
例 (x2+y2+12x+9)2−4(2x+3)3=0
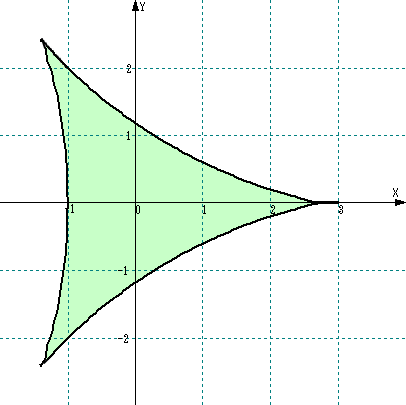
(コメント) この曲線は、三尖点曲線と言われるそうだ。フリーハンドでも書けそうな図だが、
微妙な曲線が数学らしい!
例 y2(4−x2)−(x2−4y−2)2=0
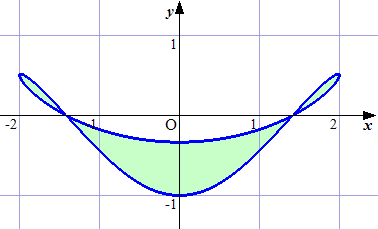
(コメント) この曲線は、2角曲線と言われるそうだ。
角と言われれば角だが、耳にも見えるネ!
ks さんからのコメントです。(令和5年8月6日付け)
不等式 |x|+|y|≦1 や x2+y2≦1 で表される領域は、それぞれ正方形と円になる。
このように、連立式ではなくて、一つの式で、長方形や三角形を表すことができるでしょうか?
(コメント) 参考 → 「絶対値について」
らすかるさんからのコメントです。(令和5年8月6日付け)
不等号すら使わずにできます。以下は、すべて内部を含む領域です。
・4頂点が (-1,1)、(-1,-1)、(1,-1)、(1,1) である正方形(辺が軸に平行)
→ |1−x|+|1+x|+|1−y|+|1+y|=4
・4頂点が (0,1)、(-1,0)、(0,-1)、(1,0) である正方形(頂点が軸上)
→ |1−x−y|+|1−x+y|+|1+x−y|+|1+x+y|=4
・半径1の円
→ x2+y2+|x2+y2−1|=1
・横の長さがa、縦の長さがbの長方形
→ |a−2x|+|a+2x|+|b−2y|+|b+2y|=2(a+b)
・重心が原点で、一つの頂点が (0,a) である正三角形
→ |a+x
・重心が原点で、一つの頂点が (0,a) である正六角形
→ |a
+|a
・3頂点が (a,b)、(c,d)、(e,f) である三角形
→ |(ad−bc+bx−dx+cy−ay)(ad−bc+be−de+cf−af)|
+|(cf−de+dx−fx+ey−cy)(cf−de+da−fa+eb−cb)|
+|(eb−fa+fx−bx+ay−ey)(eb−fa+fc−bc+ad−ed)|=(ad+cf+eb−bc−de−fa)2
ks さんからのコメントです。(令和5年8月7日付け)
らすかるさん、ありがとうございます。驚きの結果ですね。値がうまく相殺されるのですね。
円や六角形、自由な三角形も方程式で!絶対値は、場合分けなど不便の記号だとばか
り思っていましたが、便利な記号なんですね。
GAI さんからのコメントです。(令和5年8月10日付け)
・3頂点が (a,b)、(c,d)、(e,f) である三角形
→ |(ad−bc+bx−dx+cy−ay)(ad−bc+be−de+cf−af)|
+|(cf−de+dx−fx+ey−cy)(cf−de+da−fa+eb−cb)|
+|(eb−fa+fx−bx+ay−ey)(eb−fa+fc−bc+ad−ed)|=(ad+cf+eb−bc−de−fa)2
について計算していたら、
(ad-bc+be-de+cf-af)=(cf-de+da-fa+eb-cb)=(eb-fa+fc-bc+ad-ed)=(ad+cf+eb-bc-de-fa)
が成り立つようなんです。従って、求める式は、
|ad-bc+bx-dx+cy-ay|+|cf-de+dx-fx+ey-cy|+|eb-fa+fx-bx+ay-ey|=|ad+cf+eb-bc-de-fa|
と表してはいけませんかね?
らすかるさんからのコメントです。(令和5年8月10日付け)
確かにそうですね。全く気づきませんでした。
以下、工事中!