愨懳抣偵偮偄偰丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暘偐偭偰偟傑偊偽壗偱傕側偄偑丄暘偐傞傑偱偑戝曄偩偲偄偆傕偺偺戙昞偑乽愨懳抣乿偱偁
傠偆丅偦偺棟桼偲偟偰丄愨懳抣偺嫵偊曽偑偄傠偄傠偁傞偙偲偵尨場偑偁傞偲巚傢傟傞丅
丂弶婜偺抜奒偱偼丄幚悢偺愨懳抣偲偼丄偦偺悢偐傜晧偺晞崋傪庢傝彍偄偨傕偺偲偟偰嫵偊
傜傟傞丅偙偺傛偆側峫偊曽偼丄愨懳抣偺杮棃偺堄枴偵崻偞偡傕偺偱丄惗搆帺恎偵偲偭偰傕
棟夝偟傗偡偄偲巚偆丅
丂拞妛峑偱弶傔偰丄惓偺悢丄晧偺悢傪妛傇偑丄偨偲偊偽丄乽亄俇亅乮亄俁乯乿偺傛偆側寁嶼偵
偍偄偰丄庩峏偵丄惓偺悢傪乽亄俇乿偲彂偔偺偼丄愨懳抣掕拝偺偨傔偺晍愇側偺偩傠偆丅
| 丂 |
| 丂幚悢偼丄 |
|
亄 |
俇 |
偺傛偆偵丄晞崋偲愨懳抣偺懳偱昞偝傟傞丅 |
| 丂 |
|
乮晞崋乯 |
乮愨懳抣乯 |
丂 |
丂偟偐偟側偑傜丄崅峑偵擖傞偲丄偙偺傛偆側嫵偊曽偼捠忢側偝傟側偄丅
宍幃揑偵師偺傛偆偵掕媊偝傟傞丅
丂倃亞侽丂偺偲偒丄丂|倃|亖倃丂丄倃亙侽丂偺偲偒丄丂|倃|亖亅倃
丂宍幃揑側掕媊傪曗懌偡傞曽朄偲偟偰丄|倃| 偼丄悢捈慄忋偱丄尨揰俷乮侽乯偲揰俹乮倃乯偲偺嫍
棧傪昞偡偲偄偆擣幆傕偁傞偑丄愨懳抣杮棃偺堄枴偐傜偡傟偽丄偦偺暘偐傝偵偔偝偼丄屲廫
曕昐曕偱偁傠偆丅
丂摿偵丄|俆|亖俆丂側偳偺応崌丄栤戣偼側偄偑丄|亅俆|亖亅乮亅俆乯亖俆丂偲偄偆寁嶼偼丄惗搆偵
偲偭偰棟夝偵嬯偟傓寁嶼偺傛偆偩丅嫍棧偺峫偊傪梡偄偰丄|亅俆|亖侽亅乮亅俆乯亖俆丂偲偟偰傕
從偗愇偵悈偱偁傞丅
丂偙偺傛偆偵廗摼偡傞傑偱戝曄側愨懳抣傕丄偦偺墳梡傪尒傞偲偒丄旕忢偵枺榝揑側摥偒傪
偡傞偙偲偵婥偯偐偝傟傞丅愨懳抣偺壺楉側摥偒傪尒偢偵丄扨偵宍幃揑偵愨懳抣偲偄偆傕偺
傪嫵偊傜傟傞偺偱丄懡暘掕拝棪傕埆偄偺偩傠偆丅
丂惗搆偼丄昁梫偲擣幆偡傞傕偺偺媧廂偼偡偙傇傞傛偄偺偱丄墳梡椺傪傕偭偲嫵壢彂摍偵嶶
傝偽傔傟偽丄彮偟偼掕拝棪偺夵慞偵栶棫偮偺偱偼側偄偩傠偆偐丠
丂愨懳抣偺偮偄偨娭悢丂倷亖|倶|丂偺僌儔僼偼壓恾偺傛偆偵側傞丅
 |
丂丂丂愨懳抣偺掕媊偵廬偭偰峫偊傟偽丄梕堈偵
丂丂嵍恾偺僌儔僼傪彂偔偙偲偑偱偒傞丅
丂丂丂偙偺応崌丄娭悢丂倷亖倶丂偺僌儔僼偲偺崻杮
丂丂揑側堘偄偵婥偯偔昁梫偑偁傞丅
丂丂丂愨懳抣偺偮偄偨娭悢丂倷亖|倶|丂偺僌儔僼偼
丂丂娭悢丂倷亖倶丂偺僌儔僼偵偍偄偰丄倶幉偺壓懁
丂丂偺晹暘傪丄倶幉偵娭偟偰愜傝曉偟偰摼傜傟傞
丂丂偲偄偆偲偙傠偑杮幙揑偱偁傞丅 |
丂偙偺峫偊曽傪梡偄傟偽丄師偺娭悢偺僌儔僼偼丄擄偟偄寁嶼傪偟側偔偰傕梕堈偵憐憸偱偒傞
偩傠偆丅
椺丂娭悢丂倷亖| |倶|亅俀 | 偺僌儔僼傪彂偗丅
乮峫偊曽乯丂娭悢丂倷亖|倶|亅俀 偺僌儔僼偼丄娭悢丂倷亖|倶| 偺僌儔僼傪 倷幉曽岦偵丄亅俀偩偗暯峴
丂丂丂丂丂堏摦偟偨傕偺偱偁傞丅偦偺僌儔僼偵偍偄偰丄倶幉偺壓懁偺晹暘傪丄倶幉偵娭偟偰愜傝曉
丂丂丂丂丂偣偽傛偄丅
丂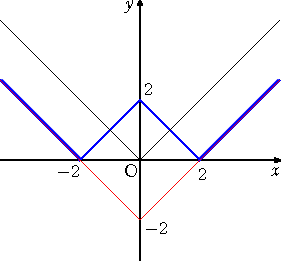
椺丂娭悢丂倷亖| | | | 倶亅俀 |亅侾 |亅俀 |亅俁 | 偺僌儔僼傪彂偗丅
丂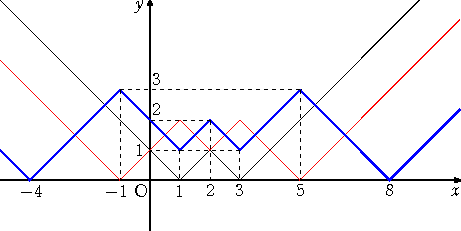
丂俀偮偺椺偐傜傕暘偐傞傛偆偵丄愨懳抣傪梡偄傞偲丄偐側傝憿宍揑偵柺敀偄僌儔僼傪彂偔偙偲
偑偱偒傞丅
丂傑偨丄師偺傛偆側惓曽宍傕愨懳抣傪梡偄偰昞偡偙偲偑偱偒傞丅
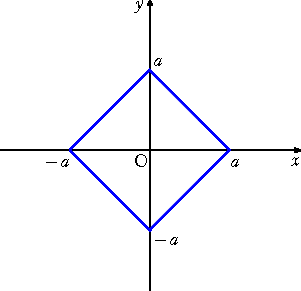 |
丂丂丂嵍恾傪昞偡曽掱幃偼丄 | 倶 | 亄 | 倷 | 亖 倎
丂丂偱梌偊傜傟傞丅
丂丂丂惓曽宍偺撪晹偍傛傃廃傪昞偡晄摍幃偼丄
丂丂| 倶 | 亄 | 倷 | 亝 倎
丂丂偱梌偊傜傟傞丅 |
丂愨懳抣傪梡偄傞偲丄師偺傛偆側僌儔僼傪彂偔偙偲傕偱偒傞丅側偤偐偼丄撉幰偺楙廗栤戣偲偟
偰巆偟偰偍偙偆丅
椺丂| | | 倶 |亅俀 |亄 | 倷 |亅俀 |亖俀
丂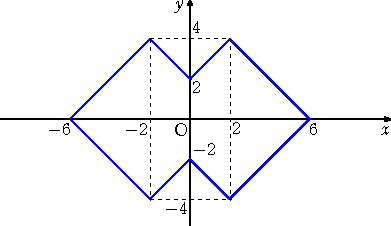
椺丂| | | 倶 |亅係 |亄 | 倷 |亅係 |亖俀

丂忋婰偺俀椺偼丄戞侾徾尷偺僌儔僼偑婎杮偱偁傞丅倶幉丄倷幉傪嬀偲巚偆偲忋偺傛偆側僌儔僼偑
摼傜傟傞丅
丂傑傞偱丄枩壺嬀傪尒偰傞傛偆側嶖妎傪妎偊傞偺偼巹偩偗偩傠偆偐丠
丂忋婰偺傛偆側暋嶨側恾宍偑丄愨懳抣傪梡偄傞偲丄偨偭偨侾杮偺幃偱昞尰偱偒傞偲偄偆偙偲偼
昅愩偵恠偔偟偑偨偄傎偳旤偟偄丅
丂摍幃傪晄摍幃偵曄偊傟偽丄偝傜偵昞忣朙偐側恾宍傪変乆偼庤偵擖傟傞偙偲偑弌棃傞丅
椺丂| 俀 | 倶 | 亄俀 | 倷 |亅俁 |亝侾
丂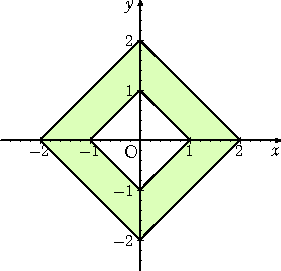 丂
丂
丂柤屆壆戝妛乮侾俋俈係乯偱師偺椞堟傪栤偆栤戣偑弌戣偝傟偨丅
丂侾亙| | 倶 |亅俀 |亄| | 倷 |亅俀 |亙俆
丂帪戙偼傔偖偭偰丄戝嶃戝妛丂慜婜棟宯乮俀侽侾俁乯偱丄帡偨傛偆側椞堟偺栤戣偑弌戣偝傟偨丅
丂侾亝| | 倶 |亅俀 |亄| | 倷 |亅俀 |亝俁
摎偊偼丄壓恾偲側傞丅
丂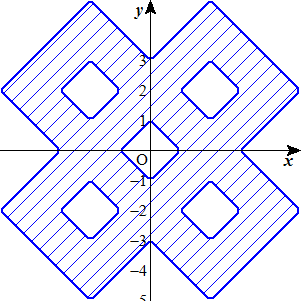
乮僐儊儞僩乯丂偙傫側偙偲傕偁傞偺偱丄庴尡偭偰夁嫀栤傪傗傞壙抣偼偁傞偺偐側丠偱傕庴尡惗偼
丂丂丂丂丂係侽擭傎偳慜偺夁嫀栤側傫偰庢傝慻傔側偄傛偹丏丏丏丅
丂崅峑俀擭偱妛傇乽悢妛嘦乿偵偍偄偰丄暯柺忋偺俀揰娫偺嫍棧偺岞幃傪妛廗偡傞丅
丂俀揰 俙乮 倶1 丆 倷1 乯丄俛乮 倶2 丆 倷2 乯傪寢傇慄暘偺挿偝 倓 偼丄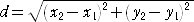
偱梌偊傜傟傞丅偙偺嫍棧偺掕媊傪梡偄傞偲丄
丂俀揰 俷乮 侽 丆 侽 乯丄俙乮 侾 丆 侾 乯偐傜摍嫍棧偁傞揰偺廤傑傝
偼丄俀揰 俙丄俛傪寢傇慄暘偺悅捈俀摍暘慄偱偁傞偙偲偑捈偪偵媮傔傜傟傞丅
丂幚嵺偵丄忦審傪枮偨偡揰偺嵗昗傪丄乮 倶 丆 倷 乯偲偡傞偲丄
丂乮倶亅侽乯2亄乮倷亅侽乯2亖乮倶亅侾乯2亄乮倷亅侾乯2
忋幃傪揥奐偟偰惍棟偡傞偲丄丂倶亄倷亅侾亖侽
丂偙傟偼丄俀揰 俙丄俛傪寢傇慄暘偺悅捈俀摍暘慄偱偁傞丅
丂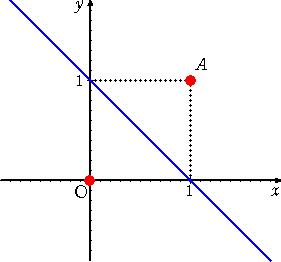
丂偲偙傠偱丄丂 丂偼丄俤倳們倢倝倓 嫍棧娭悢偲屇偽傟傞偑丄暯柺忋偵
丂偼丄俤倳們倢倝倓 嫍棧娭悢偲屇偽傟傞偑丄暯柺忋偵
掕傔傜傟傞嫍棧偼丄偙傟埲奜偵傕偨偔偝傫懚嵼偡傞丅
丂暯柺偵偍偄偰丄嫍棧 倓 偼師偺彅忦審傪枮偨偡傕偺偱偁傞丅
乮侾乯丂擟堄偺俀揰 俙丄俛 偵懳偟偰丄丂倓 乮 俙 丆 俛 乯亞侽丂摍崋惉棫偼丄丂俙亖俛丂偺偲偒偵尷傞丅
乮俀乯丂擟堄偺俀揰 俙丄俛 偵懳偟偰丄丂倓 乮 俙 丆 俛 乯亖倓 乮 俛 丆 俙 乯
乮俁乯丂擟堄偺俁揰 俙丄俛丄俠 偵懳偟偰丄丂倓 乮 俙 丆 俠 乯亝俢 乮 俙 丆 俛 乯亄倓 乮 俛 丆 俠 乯
丂暯柺忋偺俀揰 俙乮 倶1 丆 倷1 乯丄俛乮 倶2 丆 倷2 乯傪寢傇慄暘偺挿偝傪 倓1 偲偟偰丄忋婰偺忦審傪
枮偨偟丄偐偮丄俤倳們倢倝倓 嫍棧娭悢埲奜偺傕偺偲偟偰偼丄
丂倓1 亖 乥 倶1 亅 倶2 乥亄乥 倷1 亅 倷2 乥
偑桳柤偩傠偆丅偙偺嫍棧 倓1 偵偮偄偰丄愭偺栤戣
丂丂俀揰 俷乮 侽 丆 侽 乯丄俙乮 侾 丆 侾 乯偐傜摍嫍棧偁傞揰偺廤傑傝
偼丄偳偆側傞偱偁傠偆偐丠偙偺傛偆側栤偄偐偗傕悢妛揑偵戝偄偵嫽枴偑偁傞偲偙傠偱偁傞丅
丂忦審傪枮偨偡揰偺嵗昗傪丄乮 倶 丆 倷 乯偲偡傞偲丄
丂乥 倶 亅 侽 乥亄乥 倷 亅 侽 乥亖乥 倶 亅 侾 乥亄乥 倷 亅 侾 乥
偡側傢偪丄丂丂乥 倶 乥亄乥 倷 乥亖乥 倶 亅 侾 乥亄乥 倷 亅 侾 乥
乮侾乯丂倶亞侾丂丄倷亞侾丂偺偲偒丄丂倶亄倷亖倶亅侾亄倷亅侾丂傛傝丄丂侽亖亅俀丂偱晄揔丅
丂丂傛偭偰丄丂偙偺椞堟偼丄媮傔傞椞堟偵偼娷傑傟側偄丅
乮俀乯丂倶亞侾丂丄侽亝倷亙侾丂偺偲偒丄丂倶亄倷亖倶亅侾亅倷亄侾丂傛傝丄丂倷亖侽
丂丂傛偭偰丄丂倷亖侽丂乮倶亞侾丂丄侽亝倷亙侾乯偼丄媮傔傞椞堟偵偼娷傑傟傞丅
乮俁乯丂倶亞侾丂丄倷亙侽丂偺偲偒丄丂倶亅倷亖倶亅侾亅倷亄侾丂傛傝丄丂侽亖侽丂偱揔丅
丂丂傛偭偰丄丂倶亞侾丂丄倷亙侽丂偼丄媮傔傞椞堟偵偼娷傑傟傞丅
乮係乯丂侽亝倶亙侾丂丄倷亞侾丂偺偲偒丄丂倶亄倷亖亅倶亄侾亄倷亅侾丂傛傝丄丂倶亖侽丂偱揔丅
丂丂傛偭偰丄丂倶亖侽丂乮侽亝倶亙侾丂丄倷亞侾乯偼丄媮傔傞椞堟偵偼娷傑傟傞丅
乮俆乯丂侽亝倶亙侾丂丄侽亝倷亙侾丂偺偲偒丄丂倶亄倷亖亅倶亄侾亅倷亄侾丂傛傝丄丂倶亄倷亖侾
丂丂傛偭偰丄丂倶亄倷亖侾丂乮侽亝倶亙侾丂丄侽亝倷亙侾乯偼丄媮傔傞椞堟偵偼娷傑傟傞丅
乮俇乯丂侽亝倶亙侾丂丄倷亙侽丂偺偲偒丄丂倶亅倷亖亅倶亄侾亅倷亄侾丂傛傝丄丂倶亖侾丂偱晄揔丅
丂丂傛偭偰丄丂侽亝倶亙侾丂丄倷亙侽丂偼丄媮傔傞椞堟偵偼娷傑傟側偄丅
乮俈乯丂倶亙侽丂丄倷亞侾丂偺偲偒丄丂亅倶亄倷亖亅倶亄侾亄倷亅侾丂傛傝丄丂侽亖侽丂偱揔丅
丂丂傛偭偰丄丂倶亙侽丂丄倷亞侾丂偼丄媮傔傞椞堟偵偼娷傑傟傞丅
乮俉乯丂倶亙侽丂丄侽亝倷亙侾丂偺偲偒丄丂亅倶亄倷亖亅倶亄侾亅倷亄侾丂傛傝丄丂倷亖侾丂偱晄揔丅
丂丂傛偭偰丄丂倶亙侽丂丄侽亝倷亙侾丂偼丄媮傔傞椞堟偵偼娷傑傟側偄丅
乮俋乯丂倶亙侽丂丄倷亙侽丂偺偲偒丄丂亅倶亅倷亖亅倶亄侾亅倷亄侾丂傛傝丄丂侽亖俀丂偱晄揔丅
丂丂傛偭偰丄丂倶亙侽丂丄倷亙侽丂偼丄媮傔傞椞堟偵偼娷傑傟側偄丅
丂埲忋偐傜丄媮傔傞椞堟偼壓恾偺傛偆偵側傞丅
丂丂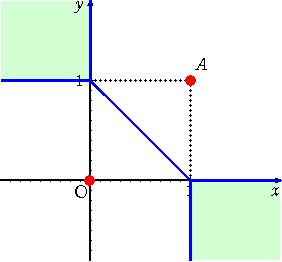
乮捛婰乯丂暯惉俀俋擭侾寧侾俋擔晅偗
丂愨懳抣娭悢偺嬃偔傋偒惈幙偵偮偄偰丄嵟嬤憳嬾偟偨偺偱傑偲傔偰偍偒偨偄丅傑偢丄師偺栤
戣傪偛棗偔偩偝偄丅
丂値偼惍悢偲偡傞丅偙偺偲偒丄
丂俽乮値乯亖乥値亅侾乥亄乥値亅俀乥亄丒丒丒亄乥値亅俋乥亄乥値亅侾侽乥丂偺愨懳抣傪奜偣丅
乮夝乯丂値亙侾丂偺偲偒丄俽乮値乯亖亅乮値亅侾乯亅乮値亅俀乯亅丒丒丒亅乮値亅侾侽乯亖亅侾侽値亄俆俆
丂値亜侾侽丂偺偲偒丄丂俽乮値乯亖乮値亅侾乯亄乮値亅俀乯亄丒丒丒亄乮値亅侾侽乯亖侾侽値亅俆俆
丂堦斒偵丄帺慠悢倠乮侾亝倠亝俋乯偵懳偟偰丄倠亝値亝倠亄侾丂偺偲偒丄
俽乮値乯亖乮値亅侾乯亄丒丒丒亄乮値亅倠乯亅乮値亅乮倠亄侾乯乯亅丒丒丒亅乮値亅俋乯亅乮値亅侾侽乯
丂亖倠乮俀値亅倠亅侾乯/俀亅乮侾侽亅倠乯乮俀値亅倠亅侾侾乯/俀
丂亖俀乮倠乕俆乯値亅倠2亅倠亄俆俆丂丂乮廔乯
丂偙偺栤戣偵偮偄偰丄懡暘懡偔偺曽偑忋婰偺傛偆偵夝偔偱偁傠偆偲巚傢傟傞丅悢妛偺僙儞僗偵
堨傟傞曽偼丄傕偟偐偟偨傜師偺傛偆偵夝偔偐傕偟傟側偄丅
丂値亙侾丄値亜侾侽偵偮偄偰偼丄忋婰偲摨偠丅
丂侾亝値亝侾侽丂偺偲偒丄
俽乮値乯亖乮値亅侾乯亄乮値亅俀乯亄丒丒丒亄乮値亅乮値亅侾乯乯
丂丂亅乮値亅乮値亄侾乯乯亅乮値亅乮値亄俀乯乯亅丒丒丒亅乮値亅俋乯亅乮値亅侾侽乯
丂亖侾亄俀亄丒丒丒亄乮値亅侾乯亄乮侾亄俀亄丒丒丒亄乮侾侽亅値乯乯
丂亖値乮値亅侾乯/俀亄乮侾侽亅値乯乮侾侾亅値乯/俀
丂亖乮値2亅値亄値2亅俀侾値亄侾侾侽乯/俀
丂亖値2亅侾侾値亄俆俆
丂偙偺傛偆偵丄俽乮値乯偑値偺俀師幃偱昞偝傟傞偲偄偆帠幚偼偁傑傝抦傜傟偰偄側偄偐傕偟傟側偄丅
丂師偺傛偆偵峫偊偰傕丄俽乮値乯偑値偺俀師幃偱昞偝傟傞偙偲偵婥偯偐偝傟傞丅偨偩偟丄偙偺傛偆側
峫偊偵帄傞偙偲偼捠忢側偄偙偲偱偁傠偆丅
丂帺慠悢倠乮侾亝倠亝俋乯偵懳偟偰丄倠亝値亝倠亄侾丂偺偲偒丄
俽乮倠乯亖乮倠亅侾乯亄丒丒丒亄乮倠亅乮倠亅侾乯乯亅乮倠亅乮倠亄侾乯乯亅丒丒丒亅乮倠亅俋乯亅乮倠亅侾侽乯
丂亖侾亄俀亄丒丒丒亄乮倠亅侾乯亄侾亄俀亄丒丒丒亄乮侾侽亅倠乯
丂亖倠乮倠亅侾乯/俀亄乮侾侽亅倠乯乮侾侾亅倠乯/俀
丂亖倠2亅侾侾倠亄俆俆
丂摨條偵偟偰丄
俽乮倠亄侾乯亖倠亄丒丒丒亄侾亅乮倠亄侾亅乮倠亄俀乯乯亅丒丒丒亅乮倠亅俉乯亅乮倠亅俋乯
丂亖倠乮倠亄侾乯/俀亄侾亄俀亄丒丒丒亄乮俋亅倠乯
丂亖倠乮倠亄侾乯/俀亄乮俋亅倠乯乮侾侽亅倠乯/俀
丂亖倠2亅俋倠亄係俆
丂傛偭偰丄丂俽乮倠亄侾乯亅俽乮倠乯亖俀倠亅侾侽丄丂俽乮侾乯亖侾亄俀亄丒丒丒亄俋亖係俆丂傛傝丄
丂俀亝値亝侾侽丂偺偲偒丄
丂俽乮値乯亖係俆亄儼倠=1乣値-1乮俀倠亅侾侽乯亖係俆亄値乮値亅侾乯亅侾侽乮値亅侾乯亖値2亅侾侾値亄俆俆
偙偺幃偼丄値亖侾偺偲偒傕惉傝棫偮丅
丂傛偭偰丄丂俽乮値乯亖値2亅侾侾値亄俆俆丂偱偁傞丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俋擭侾寧侾俋擔晅偗乯
丂忋婰偺栤戣傪尒偰丄椶戣偑偁傝傑偟偨丅侾俋俇侾擭偺嫗搒戝妛棟宯偺俆斣丅
丂値偑惍悢偱偁傞偲偒丄俽亖乥値亅1乥亄乥値亅2乥亄丒丒丒亄乥値亅100乥偺嵟彫抣傪媮
傔傛丅傑偨丄偦偺偲偒偺値偺抣傪媮傔傛丅
乮僐儊儞僩乯丂巹偺怑応偱愨懳抣偺栤戣傪榖戣偵偟偨傜丄偁傞曽偑乽偳偙偐偱夝偄偨妎偊偑偁
丂丂丂丂丂傞乿偲尵傢傟偨丅懡暘丄偙傟偺偙偲偩偭偨偺偐側丠
丂嫗搒戝妛偺栤戣傪夝偄偰傒傑偟偨丅乮暯惉俀俋擭侾寧俀侾擔晅偗乯
丂値亙侾丂偺偲偒丄丂俽乮値乯亖亅乮値亅1乯亅乮値亅2乯亅丒丒丒亅乮値亅100乯亖亅100値亄5050
丂丂傛偭偰丄値亖侽丂偺偲偒丄嵟彫抣丂5050丂傪偲傞丅
丂値亜100丂偺偲偒丄丂俽乮値乯亖乮値亅侾乯亄乮値亅俀乯亄丒丒丒亄乮値亅侾侽乯亖100値亅5050
丂丂傛偭偰丄値亖100丂偺偲偒丄嵟彫抣丂5050丂傪偲傞丅
丂侾亝値亝100丂偺偲偒丄
丂俽乮値乯亖儼倠=1乣値乮値亅倠乯亄儼倠=値+1乣100乮亅値亄倠乯
丂丂亖値2亅値乮値亄侾乯/俀亅乮100亅値乯乮101亅値乯/俀
丂丂亖値2亅101値亄5050
丂丂傛偭偰丄値亖俆侽丄俆侾丂偺偲偒丄嵟彫抣丂2500丂傪偲傞丅
丂埲忋偐傜丄媮傔傞嵟彫抣偼丄俀俆侽侽
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俋擭侾寧俀侽擔晅偗乯
丂悢妛揑堄枴傪峫偊傟偽堦暘偱夝偗傞丄嫗戝傜偟偄栤戣偱偡偹丅
丂愨懳抣傪悢捈慄忋偺俀揰偺嫍棧偲峫偊傞偲丄柧傜偐偵丄
丂丂S(50)<S(49)<S(48)<乧乧丂丄S(51)<S(52)<S(53)<乧乧
丂n=50 傑偨偼 51 偺偲偒丄
丂S= (|n-1|+|n-51|) + (|n-2|+|n-52|) + 乧乧 + (|n-50|+|n-100|)= 50亊50 = 2500
丂傛偭偰丄嵟彫抣偼 2500 乮n=50,51 偺偲偒乯
丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俋擭侾寧俀侽擔晅偗乯
丂値偼惍悢偱丄倫=1,2,3,4,5,....丂Sum[(Abs[n - k])^p, {k, 1, 100}] 偺帪偺嵟彫抣偼丠
乮捛婰乯丂椷榓俆擭係寧俁侽擔晅偗
丂杊塹堛壢戝妛峑丂堛妛嫵堢妛晹乮俀侽俀俀乯丂偱丄愨懳抣偵娭偡傞栤戣偑弌戣偝傟偨丅栤戣
偺庯巪偼丄忋婰偺嫗搒戝妛棟宯乮侾俋俇侾乯偲摨條偱偁傞丅
丂彮乆崪偺偁傞俈戣傪丄俋侽暘偱夝偐側偗傟偽側傜側偄偲偄偆拞偱偺侾栤偱丄DD++ 偝傫偺傛偆
側峫偊曽傪偡傟偽丄梫椞傛偔張棟偝傟傞偺偩傠偆丅
嘨丏丂幚悢 倶 偺娭悢 俥値乮倶乯亖儼k=1n 乥倶亅倠乥乮値亖侾丄俀丄俁丄丒丒丒乯 偑偁傞丅師偺栤偄偵摎
丂丂偊傛丅
乮侾乯丂娭悢俥3乮倶乯偺嵟彫抣傪媮傔傛丅
乮俀乯丂偁傞婏悢倣偵懳偟丄俥倣乮倶乯偺嵟彫抣偑俁侽偱偁傞偲偒丄倣偺抣傪媮傔傛丅
乮夝乯乮侾乯丂俥3乮倶乯亖乥倶亅侾乥亄乥倶亅俀乥亄乥倶亅俁乥丂偵偍偄偰丄
丂倶亙侾丂偺偲偒丄丂俥3乮倶乯亖亅倶亄侾亅倶亄俀亅倶亄俁亖亅俁倶亄俇
丂侾亝倶亙俀丂偺偲偒丄丂俥3乮倶乯亖倶亅侾亅倶亄俀亅倶亄俁亖亅倶亄係
丂俀亝倶亙俁丂偺偲偒丄丂俥3乮倶乯亖倶亅侾亄倶亅俀亅倶亄俁亖倶
丂俁亝倶丂偺偲偒丄丂俥3乮倶乯亖倶亅侾亄倶亅俀亄倶亅俁亖俁倶亅俇
丂
丂忋恾傛傝丄娭悢俥3乮倶乯偼丄倶亖俀 偺偲偒嵟彫偱丄嵟彫抣 俀
乮俀乯丂倣亖俀値亄侾丂乮値亖侽丄侾丄俀丄丒丒丒乯丂偲偍偔偲丄
丂俥倣乮倶乯亖乥倶亅侾乥亄乥倶亅俀乥亄丒丒丒亄乥倶亅乮値亄侾乯乥亄丒丒丒亄乥倶亅倣乥
乮侾乯偲摨條偵偟偰丄俥倣乮倶乯偼丄倶亖値亄侾 偺偲偒嵟彫偱丄嵟彫抣偼丄
丂俥倣乮値亄侾乯亖俀乮値亄乮値亅侾乯亄丒丒丒亄侾乯亖値乮値亄侾乯
戣堄傛傝丄丂値乮値亄侾乯亖俁侽丂側偺偱丄丂値2亄値亅俁侽亖侽
丂乮値亄俇乯乮値亅俆乯亖侽丂偱丄値 偼丄侽埲忋偺惍悢傛傝丄丂値亖俆
丂傛偭偰丄丂倣亖俀丒俆亄侾亖侾侾丂偱偁傞丅丂丂乮廔乯
乮暿夝乯丂DD++ 偝傫偺巜恓偵廬偊偽丄摎偊偼埫嶼偱媮傔傜傟傞丅
丂愨懳抣傪悢捈慄忋偺俀揰偺嫍棧偲峫偊傞偲丄柧傜偐偵丄揰乮侾丆侽乯偲乮俁丆侽乯偺拞揰偱嵟彫
偲側傞偺偱丄摿偵応崌暘偗傪偟側偔偰傕丄乮侾乯偱偼丄倶亖俀 偱嵟彫偲偄偆偙偲偑暘偐傞丅
乮俀乯傕摨條偱偁傞丅丂丂乮廔乯
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俋擭侾寧俀侽擔晅偗乯
丂p亞2 側傜丄擇奒旝暘壜擻偱丄S''(x)>0 偐偮 S'(50.5)=0 偐傜 S(50.5) 偑嵟彫側偺偼柧傜偐丅
偁偲偺寁嶼偑柺搢側偩偗偺栤戣偲巚偄傑偡丅
(捛婰)丂幚悢偠傖側偔惍悢尷掕偱偟偨偹丅偦傟偱傕幚悢奼挘偟偨傕偺偱摨條偵峫偊偰丄偁偲偼
丂丂丂丂懳徧惈偐傜 S(50)=S(51) 傪寁嶼偡傞偩偗偺丄傗偼傝柺搢側偩偗偺栤戣乧乧丅
乮捛婰乯丂暯惉俁侽擭侾俀寧俁擔晅偗
丂愨懳抣偺偮偄偨娭悢丂倷亖|倶|丂偺僌儔僼偑壓恾偺傛偆偵側傞偙偲偼丄奆偝傫丄偛懚偠偩傠偆丅
丂
丂偙偺儁乕僕偺朻摢偺曽偱丄偄偔偮偐偺愨懳抣傪娷傓娭悢偺僌儔僼傪昤偄偨丅
丂偙傟偵懳偟偰丄愜傟慄僌儔僼偐傜偦偺娭悢幃傪応崌暘偗偡傞偙偲側偔堦偮偺幃偱昞偡偙偲傪
峫偊偨偄
乮婎杮揑側媄乯
丂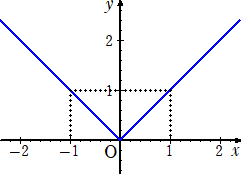
丂忋恾傪昞偡娭悢偼丄丂倷亖|倶|丂偱偁傞丅偙偺偙偲傪堦斒壔偟偰丄
乮侾乯丂倶幉曽岦偺暯峴堏摦
丂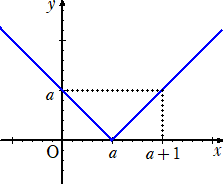
丂忋恾傪昞偡娭悢偼丄丂倷亖|倶亅倎|丂偱偁傞丅
乮俀乯丂倷幉曽岦偺奼戝丒弅彫
丂
丂忋恾傪昞偡娭悢偼丄丂倷亖倎|倶|丂偱偁傞丅
乮俁乯丂孹偒侽偐傜孹偒倎偵曄壔
丂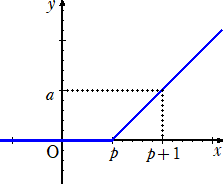
丂忋恾傪昞偡娭悢偼丄丂倷亖乮倎/俀乯乮|倶亅倫|亄倶亅倫乯丂偱偁傞丅
乮係乯丂孹偒偑亅倎偐傜侽丄偦偟偰倎偲曄壔
丂
丂忋恾傪昞偡娭悢偼丄丂倷亖乮倎/俀乯乮|倶亄倫|亄|倶亅倫|亅俀倫乯丂偱偁傞丅
丂偄偔偮偐偺墳梡戣傪峫偊偰傒傛偆丅
栤戣侾丂孹偒偑亅倎偐傜倐丄偦偟偰倎偲曄壔偡傞愜傟慄僌儔僼偺幃傪媮傔傛丅
乮夝乯
丂
丂忋恾傪昞偡娭悢偼丄
丂倷亖乷乮倎亄倐乯/俀乸|倶亄倫|亄乷乮倎亅倐乯/俀乸|倶亅倫|亅乮倎亅倐乯倫
偱偁傞丅
丂幚嵺偵丄倷亖倣|倶亄倫|亄値|倶亅倫|亄倠丂偲偍偄偰丄孹偒偵拲栚偡傞偲丄
丂倣亄値亖倎丂丄丂倣亅値亖倐
偐傜丄丂倣亖乮倎亄倐乯/俀丂丄値亖乮倎亅倐乯/俀丂偱偁傞丅
丂倶亖亅倫丂偺偲偒丄丂倷亖俀倫値亄倠亖侽
丂倶亖倫丂偺偲偒丄丂倷亖俀倫倣亄倠亖亅倎
丂壗傟偵偟偰傕丄丂倠亖亅乮倎亅倐乯倫丂傪摼傞丅丂丂乮廔乯
丂忋婰偱偼嵍抂偲塃抂偺孹偒偑亅侾攞偺娭學偵偁傝丄偁傞堄枴偱嵍塃懳徧偺娭學偵偁傞丅
丂偦傟偱偼丄嵍塃旕懳徧偺応崌偺愜傟慄僌儔僼偺幃傪嶌偭偰傒傛偆丅
椺偊偽丄師偺愜傟慄僌儔僼偼偳偆偩傠偆丠
丂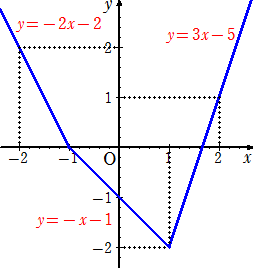
丂孹偒偑丄亅俀仺亅侾仺俁丂偲曄壔偡傞偺偱丄倷亖倣|倶亄侾|亄値|倶亅侾|丂偵偍偄偰丄
丂亅倣亅値亖亅俀丂丄倣亅値亖亅侾丂丄倣亄値亖俁
偲偟偰偟傑偆偲戞侾幃偲戞俁幃偱柕弬偑惗偠傞丅偙偺柕弬傪夞旔偡傞偵偼孹偒偦偺傕偺偱偼側
偔丄孹偒偺憹暘偵拝栚偡傟偽傛偄丅
丂孹偒偺憹暘偼丄丂侾仺係丂偲曄壔偡傞偺偱丄
丂倣亅値亅乮亅倣亅値乯亖侾丂偡側傢偪丄丂俀倣亖侾丂傛傝丄丂倣亖侾/俀
丂倣亄値亅乮倣亅値乯亖係丂偡側傢偪丄丂俀値亖係丂傛傝丄丂値亖俀
丂傛偭偰丄丂倷亖乮侾/俀乯|倶亄侾|亄俀|倶亅侾|丂傪摼傞丅
丂偨偩丄偙偺娭悢偺孹偒偼丄亅俆/俀仺亅俁/俀仺俆/俀丂偲曄壔偡傞偺偱丄孹偒偺曄壔傪丄
亅俀仺亅侾仺俁丂偲偡傞偨傔偵丄堦棩偵孹偒偵丂侾/俀傪壛偊傟偽傛偄丅
丂偡側傢偪丄娭悢幃偼丄丂倷亖乮侾/俀乯|倶亄侾|亄俀|倶亅侾|亄乮侾/俀乯倶丂偲側傞丅
丂倶亖亅侾偺偲偒丄倷亖係亅侾/俀亖俈/俀丂側偺偱丄倶亖亅侾丂偺偲偒丄倷亖侽丂偲偡傞偨傔偵丄
媮傔傞娭悢幃偼丄丂倷亖乮侾/俀乯|倶亄侾|亄俀|倶亅侾|亄乮侾/俀乯倶亅俈/俀丂偲側傞丅
丂侾師娭悢丂倷亖們倶亄倓丂傪娭悢幃偵壛偊偰傕丄孹偒偺憹暘偵曄壔偼側偄偺偱丄弶傔偐傜媮傔
傞幃傪丄
丂丂丂丂丂丂倷亖倣|倶亄侾|亄値|倶亅侾|亄們倶亄倓
偲抲偄偰傕傛偄偙偲偵婥偑偮偔丅偙偺偲偒丄師偺楢棫曽掱幃偑摼傜傟傞丅
丂亅倣亅値亄們亖亅俀丂丄倣亅値亄們亖亅侾丂丄倣亄値亄們亖俁
丂偙傟傪夝偔偲丄丂倣亖侾/俀丂丄値亖俀丂丄們亖侾/俀丂偱丄
丂丂倷亖乮侾/俀乯|倶亄侾|亄俀|倶亅侾|亄乮侾/俀乯倶亄倓
丂倶亖亅侾丂偺偲偒丄丂倷亖係亅侾/俀亄倓亖侽丂傛傝丄丂倓亖亅俈/俀
丂傛偭偰丄媮傔傞娭悢幃偼丄丂倷亖乮侾/俀乯|倶亄侾|亄俀|倶亅侾|亄乮侾/俀乯倶亅俈/俀丂偲側傞丅
乮僐儊儞僩乯丂偙偪傜偺曽偑傛傝幚愴揑偱偡偹両
栤 戣丂丂乥倶亅俀乥亄乥倷亅俀乥亝侾丂偺偲偒丄倷/倶亄倶/倷偺嵟戝抣丒嵟彫抣傪媮傔傛丅
乮夝乯丂倷/倶亖倣丂偲偍偔偲丄侾/俀亝倣亝俀
丂丂丂倸亖倣亄侾/倣丂偲偍偔偲丄丂倸乫亖侾亅侾/倣2亖乮倣亄侾乯乮倣亅侾乯/倣2丂傛傝丄倣亖亇侾
丂倣亖侾偺偲偒嬌彫偐偮嵟彫偱丄嵟彫抣偼俀
丂倣亖侾/俀丄俀偺偲偒丄嵟戝抣偼俆/俀丂丂乮廔乯
丂愨懳抣偺偮偄偨侾師娭悢偺僌儔僼偼愜傟慄偲偄偆僀儊乕僕偩偑丄偦偺僀儊乕僕偲偼偐偗棧
傟偨椺偑偁傞丅
丂|倷亄侾|亄 |倷亅侾|亖 |倶亄侾|亄 |倶亅侾|
丂倷亙亅侾丂偺偲偒丄丂亅倷亅侾亅倷亄侾亖 |倶亄侾|亄 |倶亅侾|丂傛傝丄倷亖亅乮|倶亄侾|亄 |倶亅侾|乯/俀
丂丂倶亙亅侾丂偺偲偒丄丂倷亖倶
丂丂亅侾亝倶亙侾丂偺偲偒丄丂倷亖亅侾
丂丂倶亞侾丂偺偲偒丄丂倷亖亅倶
亅侾亝倷亙侾丂偺偲偒丄丂倷亄侾亅倷亄侾亖 |倶亄侾|亄 |倶亅侾|丂傛傝丄丂|倶亄侾|亄 |倶亅侾|亖俀
丂丂倶亙亅侾丂偺偲偒丄丂亅倶亅侾亅倶亄侾亖俀丂傛傝丄丂倶亖亅侾乮晄揔乯
丂丂亅侾亝倶亙侾丂偺偲偒丄丂倶亄侾亅倶亄侾亖俀丂傛傝丄丂偄偮傕惉棫側偺偱丄丂亅侾亝倶亙侾
丂丂倶亞侾丂偺偲偒丄丂倶亄侾亄倶亅侾亖俀丂傛傝丄丂倶亖侾乮揔乯
丂偙偺偲偒丄丂亅侾亝倶亝侾
倷亞侾丂偺偲偒丄丂倷亄侾亄倷亅侾亖|倶亄侾|亄 |倶亅侾|丂傛傝丄丂倷亖乮|倶亄侾|亄 |倶亅侾|乯/俀
丂丂倶亙亅侾丂偺偲偒丄丂倷亖亅倶
丂丂亅侾亝倶亙侾丂偺偲偒丄丂倷亖侾
丂丂倶亞侾丂偺偲偒丄丂倷亖倶
丂埲忋傪恾帵偡傞偲丄
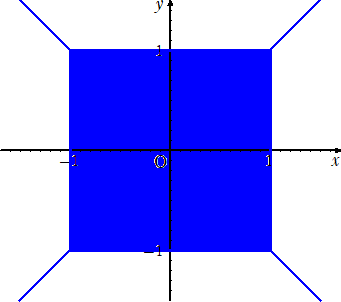
偲側傝丄愜傟慄偲偼堘偆乽椞堟乿偑尰傟偨丅
丂倠倱偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俋寧侾俇擔晅偗乯
丂捈慄偺愊偺晄摍幃偵傛傞椞堟偼丄惓椞堟偲晧椞堟偵嫬奅傪傑偨偄偱曄壔偟傑偡丅
乥倶倷乥亜侽偺応崌偼丄嫬奅傪傑偨偄偱傕丄晞崋偑曄壔偟側偄偲偙傠偑柺敀偄丅
乮捛婰乯丂椷榓俇擭侾侾寧俀擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉係乯偺栤戣偼丄愨懳抣偺偮偄偨嵟彫抣偵娭偡傞栤戣偱偁傞丅
栤戣俆丂丂値傪帺慠悢偲偟丄俥乮倶乯亖儼k=12n 乥倶亅俁k乥偲偡傞丅
乮侾乯丂倶 偑幚悢慡懱傪摦偔偲偒丄俥乮倶乯偺抣傪嵟彫偵偡傞傛偆側幚悢 倶 偺廤崌傪媮傔傛丅
乮俀乯丂俥乮倶乯偺嵟彫抣傪 倎値 偲偡傞偲偒丄倎値 偍傛傃 倢倝倣n仺亣 倎値/俋値 傪媮傔傛丅
乮夝乯乮侾乯丂俥乮倶乯偺僌儔僼偺摿挜偐傜丄俁n亝倶亝俁n+1 偱嵟彫偱偁傞丅
乮俀乯丂倎n亖俁n+1亄俁n+2亄丒丒丒亄俁2n亅乮俁亄俁2亄丒丒丒亄俁n乯亖乮俁n亅侾乯乮俁亄俁2亄丒丒丒亄俁n乯
偡側傢偪丄丂倎n亖乮俁/俀乯乮俁n亅侾乯2丂偲側傞丅
偙偺偲偒丄倎値/俋値亖乮俁/俀乯乮侾亅侾/俁n乯2丂仺丂俁/俀
偡側傢偪丄丂倢倝倣n仺亣 倎値/俋値亖俁/俀丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾俀寧侾俇擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俉乯偺栤戣偼丄愨懳抣偺偮偄偨娭悢偺僌儔僼傪昤偔栤戣偱偁傞丅
栤戣俁丂丂娭悢
丂丂
偵偮偄偰丄師偺栤偵摎偊傛丅
乮侾乯丂嬌抣傪媮傔傛丅
乮俀乯丂嬋慄 倷亖俥乮倶乯 偺慟嬤慄傪媮傔傛丅
乮俁乯丂嬋慄 倷亖俥乮倶乯 偺奣宍傪偐偗丅
乮夝乯乮侾乯丂乮俀倶2亄倶亅侾乯/乮倶亅侾乯亖乮俀倶亅侾乯乮倶亄侾乯/乮倶亅侾乯亞侽丂偡側傢偪丄
丂乮俀倶亅侾乯乮倶亄侾乯乮倶亅侾乯亞侽丂倶亗侾丂傛傝丄丂亅侾亝倶亝侾/俀丂丄侾亙倶丂偺偲偒丄
丂俥乮倶乯亖乮俀倶2亄倶亅侾乯/乮倶亅侾乯亖俀倶亄俁亄俀/乮倶亅侾乯
丂俥乫乮倶乯亖俀亅俀/乮倶亅侾乯2亖俀倶乮倶亅俀乯/乮倶亅侾乯2亖侽丂偲偍偔偲丄丂倶亖侽丄俀
傑偨丄丂倶亙亅侾丂丄侾/俀亙倶亙侾丂偺偲偒丄乮俀倶2亄倶亅侾乯/乮倶亅侾乯亙侽丂側偺偱丄
丂俥乮倶乯亖亅乮俀倶2亄倶亅侾乯/乮倶亅侾乯亖亅俀倶亅俁亅俀/乮倶亅侾乯
丂俥乫乮倶乯亖亅俀亄俀/乮倶亅侾乯2亖亅俀倶乮倶亅俀乯/乮倶亅侾乯2亖侽丂偲側傞 倶 偼側偄丅
埲忋偐傜丄憹尭昞偼丄
丂丂
傛偭偰丄倶亖亅侾 偺偲偒丄嬌彫抣 侽丄倶亖侽 偺偲偒丄嬌戝抣 侾丄倶亖侾/俀 偺偲偒丄嬌彫抣 侽丄
丂倶亖俀 偺偲偒丄嬌彫抣 俋
乮俀乯丂乮侾乯傛傝丄慟嬤慄偼丄丂倶亖侾丂丄倷亖俀倶亄俁丂丄倷亖亅俀倶亅俁
乮俁乯丂亅侾亝倶亝侾/俀丂丄侾亙倶丂偺偲偒丄
丂俥乫乮倶乯亖俀亅俀/乮倶亅侾乯2丂傪偝傜偵旝暘偟偰丄俥乭乮倶乯亖係/乮倶亅侾乯3 偐傜丄
丂亅侾亝倶亝侾/俀丂偺偲偒丄俥乭乮倶乯亙侽丂偐傜丄忋偵撌
丂侾亙倶丂偺偲偒丄俥乭乮倶乯亜侽丂偐傜丄壓偵撌
丂倶亙亅侾丂丄侾/俀亙倶亙侾丂偺偲偒丄
丂俥乫乮倶乯亖亅俀亄俀/乮倶亅侾乯2丂傪偝傜偵旝暘偟偰丄俥乭乮倶乯亖亅係/乮倶亅侾乯3 偐傜丄
丂倶亙亅侾丂偺偲偒丄俥乭乮倶乯亜侽丂偐傜丄壓偵撌
丂侾/俀亙倶亙侾丂偺偲偒丄俥乭乮倶乯亜侽丂偐傜丄壓偵撌
埲忋偐傜丄嬋慄 倷亖俥乮倶乯 偺奣宍偼壓恾丅
丂丂 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧俀俇擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俀乯偺栤戣偼丄愨懳抣偺偮偄偨娭悢偺嬌抣傪媮傔傞栤戣
偱偁傞丅
栤戣丂丂娭悢 俥乮倶乯亖乮倶2亄侾亄乥俇倶亅俉乥乯/乮俀乮倶2亄侾乯乯 偺嬌抣傪媮傔傛丅
乮夝乯丂俥乮倶乯亖侾/俀亄乥俁倶亅係乥/乮倶2亄侾乯 偵偍偄偰丄
倶亞係/俁 偺偲偒丄丂俥乮倶乯亖侾/俀亄乮俁倶亅係乯/乮倶2亄侾乯丂傛傝丄
丂俥乫乮倶乯亖亅乮俁倶亄侾乯乮倶亅俁乯/乮倶2亄侾乯2亖侽丂偐傜丄丂倶亖俁
倶亙係/俁 偺偲偒丄丂俥乮倶乯亖侾/俀亅乮俁倶亅係乯/乮倶2亄侾乯丂傛傝丄
丂俥乫乮倶乯亖乮俁倶亄侾乯乮倶亅俁乯/乮倶2亄侾乯2亖侽丂偐傜丄丂倶亖亅侾/俁
傛偭偰丄師偺憹尭昞傪摼傞丅
丂
埲忋偐傜丄
倶亖亅侾/俁 偺偲偒丄嬌戝抣 俆丄倶亖係/俁 偺偲偒丄嬌彫抣 侾/俀丄倶亖俁 偺偲偒丄嬌戝抣 侾丂乮廔乯
乮僐儊儞僩乯丂嶲峫傑偱偵丄娭悢 俥乮倶乯偺僌儔僼偼壓恾偺傛偆偱偁傞丅
丂丂
乮捛婰乯丂椷榓俈擭俇寧侾俉擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俆乯偺栤戣偼丄愨懳抣偺偮偄偨娭悢偺僌儔僼傪昤偔栤戣偱
偁傞丅
栤戣丂丂娭悢 倷亖亅倶4亄倶3亄倶2亅倶亅乥倶4亄倶3亅倶2亅倶乥 偺憹尭傪挷傋丄偦偺僌儔僼傪偐
丂丂偗丅
乮夝乯丂倶4亄倶3亅倶2亅倶亖倶乮倶亅侾乯乮倶亄侾乯2丂傛傝丄
丂倶亝侽丄侾亝倶丂偺偲偒丄丂倶4亄倶3亅倶2亅倶亞侽丂側偺偱丄丂倷亖亅俀倶4亄俀倶2
丂偙偺偲偒丄丂倷乫亖亅俉倶3亄係倶亖亅係倶乮俀倶2亅侾乯亖侽丂傛傝丄丂倶亖侽丄亇侾/
丂侽亝倶亝侾丂偺偲偒丄丂倶4亄倶3亅倶2亅倶亝侽丂側偺偱丄丂倷亖俀倶3亅俀倶
丂偙偺偲偒丄丂倷乫亖俇倶2亅俀亖俀乮俁倶2亅侾乯亖侽丂傛傝丄丂倶亖亇侾/
丂埲忋偐傜丄憹尭昞偼丄
丂丂
偲側傝丄倶亖亅侾/ 偺偲偒丄嬌戝偱丄嬌戝抣 侾/俀
偺偲偒丄嬌戝偱丄嬌戝抣 侾/俀
丂倶亖侾/ 偺偲偒丄嬌彫偱丄嬌彫抣 亅係
偺偲偒丄嬌彫偱丄嬌彫抣 亅係 /俋
/俋
丂倶亖侾 偺偲偒丄嬌戝偱丄嬌戝抣 侽
偱偁傞丅僌儔僼偼壓恾丅
丂丂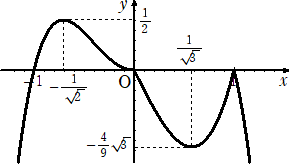
乮捛婰乯丂椷榓俈擭俇寧俀俆擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俆乯偺栤戣偼丄忋婰偲摨庯巪偺栤戣偱偁傞丅
栤戣丂丂倎亜俀 偲偟丄俥乮倶乯亖倶2倕丱乮亅乥倶亅倎乥乯 偲偡傞丅
乮侾乯丂俥乮倶乯偺嬌抣傪媮傔傛丅
乮俀乯丂嬌尷抣 倢倝倣倎仺亄亣 乮侾/倎2乯佺-aa 俥乮倶乯倓倶 傪媮傔傛丅
乮夝乯乮侾乯丂倶亙倎丂偺偲偒丄丂俥乮倶乯亖倶2倕丱乮倶亅倎乯丂偱丄俥乫乮倶乯亖乮倶2亄俀倶乯倕丱乮倶亅倎乯
丂倶亞倎丂偺偲偒丄丂俥乮倶乯亖倶2倕丱乮亅倶亄倎乯丂偱丄俥乫乮倶乯亖亅乮倶2亅俀倶乯倕丱乮倶亅倎乯
憹尭昞偼丄
丂丂
傛偭偰丄丂倶亖亅俀丂偺偲偒丄嬌戝偱丄嬌戝抣丂係倕-2-a
丂倶亖侽丂偺偲偒丄嬌彫偱丄嬌彫抣丂侽
丂倶亖倎丂偺偲偒丄嬌戝偱丄嬌戝抣丂倎2
乮俀乯丂亅倎亝倶亝倎丂側偺偱丄丂俥乮倶乯亖倶2倕丱乮倶亅倎乯
偙偺偲偒丄
佺-aa 俥乮倶乯倓倶亖佺-aa 倶2倕丱乮倶亅倎乯倓倶亖[倶2倕丱乮倶亅倎乯]-aa亅俀佺-aa 倶倕丱乮倶亅倎乯倓倶
亖倎2亅倎2倕-2a亅俀乮[倶倕丱乮倶亅倎乯]-aa亅佺-aa 倕丱乮倶亅倎乯倓倶乯
亖倎2亅倎2倕-2a亅俀乮倎亄倎倕-2a亅[倕丱乮倶亅倎乯]-aa乯
亖倎2亅俀倎亅乮倎2亄俀倎乯倕-2a亄俀乮侾亅倕-2a乯
亖倎2亅俀倎亄俀亅乮倎2亄俀倎亄俀乯倕-2a
側偺偱丄丂乮侾/倎2乯佺-aa 俥乮倶乯倓倶亖侾亅俀乮倎亅侾乯/倎2亅乮侾亄俀乮倎亄侾乯/倎2乯倕-2a丂仺丂侾
傛偭偰丄丂倢倝倣倎仺亄亣 乮侾/倎2乯佺-aa 俥乮倶乯倓倶亖侾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧俀俋擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俆乯偺栤戣偼丄婎杮栤戣偩傠偆丅
栤戣丂丂娭悢俥乮倶乯丄俧乮倶乯傪丂俥乮倶乯亖乥倶2亄俀倶乥亅倶2亅俀倶丂丄俧乮倶乯亖佺-2x 俥乮倲乯倓倲丂偱掕
丂丂傔傞丅偨偩偟丄倶 偼偡傋偰偺幚悢傪摦偔傕偺偲偡傞丅
乮侾乯丂倷亖俥乮倶乯偺僌儔僼傪偐偗丅
乮俀乯丂倷亖俧乮倶乯偺僌儔僼傪偐偗丅
乮俁乯丂嬋慄 倷亖俧乮倶乯偺愙慄偱丄孹偒偑俁/俀偱偁傞傕偺傪偡傋偰媮傔傛丅
乮夝乯乮侾乯丂倶亝亅俀丄侽亝倶丂偺偲偒丄丂俥乮倶乯亖侽
丂亅俀亙倶亙侽丂偺偲偒丄丂俥乮倶乯亖亅俀倶2亅係倶
傛偭偰丄倷亖俥乮倶乯偺僌儔僼偼壓恾丅
丂丂
乮俀乯丂倶亝亅俀丂偺偲偒丄丂俧乮倶乯亖侽
丂亅俀亙倶亙侽丂偺偲偒丄
丂俧乮倶乯亖佺-2x 乮亅俀倲2亅係倲乯倓倲亖[亅乮俀/俁乯倲3亅俀倲2]-2x亖亅乮俀/俁乯倶3亅俀倶2亄俉/俁
丂倶亞侽丂偺偲偒丄丂俧乮倶乯亖佺-20 乮亅俀倲2亅係倲乯倓倲亖俉/俁
傛偭偰丄倷亖俧乮倶乯偺僌儔僼偼壓恾丅
丂丂
乮俁乯丂俧乫乮倶乯亖亅俀倶2亅係倶亖俁/俀丂傛傝丄丂係倶2亄俉倶亄俁亖侽丂偐傜丄乮俀倶亄侾乯乮俀倶亄俁乯亖侽
傛偭偰丄丂倶亖亅侾/俀丂丄亅俁/俀
倶亖亅侾/俀丂偺偲偒丄丂倷亖俋/係丂側偺偱丄愙慄偺曽掱幃偼丄
丂倷亖乮俁/俀乯乮倶亄侾/俀乯亄俋/係亖乮俁/俀乯倶亄俁
倶亖亅俁/俀丂偺偲偒丄丂倷亖俆/侾俀丂側偺偱丄愙慄偺曽掱幃偼丄
丂倷亖乮俁/俀乯乮倶亄俁/俀乯亄俆/侾俀亖乮俁/俀乯倶亄俉/俁丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧俀係擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俈乯偺栤戣偼丄乥倶乥亖亇倶 偲偄偆擣幆偑億僀儞僩偩傠偆丅
扨弮偵丄暯曽偟偰偟傑偆偲廂廍偑偮偐側偔側傞丅応崌暘偗偡傞偺傕戝曄偦偆両
栤戣丂丂倶倷暯柺忋偺俀偮偺嬋慄丂倷亖倶2亄侾丄倷亖乥乮倶亄侾乯乮倶亅倎乯乥/俀丂偑嫟桳揰傪傕偨側
丂丂偄偲偒丄幚悢 倎 偺懚嵼偡傞斖埻傪媮傔傛丅
乮夝乯丂倶2亄侾亖乥乮倶亄侾乯乮倶亅倎乯乥/俀丂偡側傢偪丄丂倶2亄侾亖亇乮倶亄侾乯乮倶亅倎乯/俀丂偐傜丄
丂俀倶2亄俀亖亇乮倶2亄乮侾亅倎乯倶亅倎乯
傛偭偰丄丂倶2亅乮侾亅倎乯倶亄倎亄俀亖侽丂傑偨偼丄丂俁倶2亄乮侾亅倎乯倶亅倎亄俀亖侽
偙偺偳偪傜偺俀師曽掱幃偵傕幚悢夝偑側偗傟偽傛偄丅
敾暿幃俢1亖乮侾亅倎乯2亅係乮倎亄俀乯亖倎2亅俇倎亅俈亖乮倎亅俈乯乮倎亄侾乯亙侽丂傛傝丄亅侾亙倎亙俈
敾暿幃俢2亖乮侾亅倎乯2亄侾俀乮倎亅俀乯亖倎2亄侾侽倎亅俀俁亙侽丂傛傝丄亅俆亅係 亙倎亙亅俆亄係
亙倎亙亅俆亄係
偟偨偑偭偰丄媮傔傞幚悢 倎 偺懚嵼偡傞斖埻偼丄丂亅侾亙倎亙亅俆亄係 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俉寧侾俀擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俈乯偺栤戣偼丄愨懳抣偵娭傢傞掕斣偺栤戣偩傠偆丅
栤戣丂丂倎 傪 侽亙倎亙侾 傪枮偨偡掕悢偲偡傞丅
乮侾乯丂娭悢 俥乮倶乯亖倶乥倶亅倎乥偺僌儔僼偺奣宍傪偐偗丅
乮俀乯丂愊暘 俧乮倎乯亖佺01 倶乥倶亅倎乥倓倶 偺抣傪嵟彫偵偡傞 倎 傪媮傔傛丅
乮夝乯乮侾乯丂俥乮倶乯亖倶乥倶亅倎乥偺僌儔僼偺奣宍偼丄
丂丂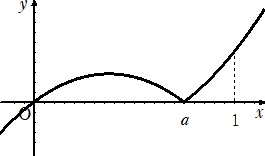
乮俀乯丂俧乮倎乯亖佺0a 乮亅倶2亄倎倶乯倓倶 亄佺a1 乮倶2亅倎倶乯倓倶 亖乮侾/俁乯倎3亅乮侾/俀乯倎亄侾/俁
丂俧乫乮倎乯亖倎2亅乮侾/俀乯亖侽丂傛傝丄丂倎亖侾/ 丂偱丄俧乮倎乯偼嬌彫偐偮嵟彫丂丂乮廔乯
丂偱丄俧乮倎乯偼嬌彫偐偮嵟彫丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俉寧侾俋擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俉乯偺栤戣偼丄僌儔僼傪堄幆偟偰夝偔栤戣偱偁傞丅
栤戣丂丂倶 偺曽掱幃 倶2亄倎乥倶亅侾乥亄倐亖侽 偑堎側傞幚悢夝傪偪傚偆偳俀屄傕偮偲偒丄
丂丂揰乮倎丆倐乯偺懚嵼偡傞斖埻傪倎倐暯柺偵恾帵偣傛丅
乮夝乯丂倷亖倶2亄倎乥倶亅侾乥亄倐丂偲偍偔丅
倶亞侾 偺偲偒丄倷亖倶2亄倎乮倶亅侾乯亄倐亖乮倶亄倎/俀乯2亅倎2/係亅倎亄倐丂偱丄幉偼丄倶亖亅倎/俀
倶亝侾 偺偲偒丄倷亖倶2亅倎乮倶亅侾乯亄倐亖乮倶亅倎/俀乯2亅倎2/係亄倎亄倐丂偱丄幉偼丄倶亖倎/俀
丂亅倎/俀亝亅侾丂懄偪丄丂倎亞俀丂偺偲偒丄丂倎/俀亞侾丂側偺偱丄倷 偺嵟彫抣偼丄倶亖侾丂偺偲偒偱丄
嵟彫抣丂倐亄侾丂偲側傞偙偲偐傜丄戣堄傪枮偨偡偨傔偵偼丄丂倐亄侾亙侽丂懄偪丄丂倐亙亅侾
丂亅侾亝亅倎/俀亝侾丂懄偪丄丂亅俀亝倎亝俀丂偺偲偒丄丂倎/俀亝侾丂側偺偱丄倷 偺嵟彫抣偼丄
倶亖倎/俀丂偺偲偒偱丄嵟彫抣丂亅倎2/係亄倎亄倐丂偲側傞偙偲偐傜丄戣堄傪枮偨偡偨傔偵偼丄
丂亅倎2/係亄倎亄倐亙侽丂懄偪丄丂倐亙倎2/係亅倎亖乮倎亅俀乯2/係亅侾
丂亅倎/俀亞侾丂懄偪丄丂倎亝亅俀丂偺偲偒丄丂倎/俀亝亅侾丂偱丄亅倎2/係亄倎亄倐亙亅倎2/係亅倎亄倐
傛傝丄戣堄傪枮偨偡偨傔偵偼丄亅倎2/係亄倎亄倐亙侽亙亅倎2/係亅倎亄倐丂傑偨偼丂倐亄侾亙侽
懄偪丄丂乮倎亄俀乯2/係亅侾亙倐亙乮倎亅俀乯2/係亅侾丂傑偨偼丂倐亙亅侾
丂埲忋偐傜丄媮傔傞揰乮倎丆倐乯偺懚嵼偡傞斖埻偼丄壓恾丅偨偩偟丄嫬奅慄偼娷傑側偄偑丄
揰乮亅俀丆亅侾乯偺傒娷傓丅
丂丂 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧俇擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俉乯偺栤戣傕丄僌儔僼傪堄幆偟偰夝偔栤戣偱偁傞丅
栤戣丂丂幚悢倠偺抣偑曄傢傞偲偒丄曻暔慄 倷亖倶2亄倠 偲嬋慄 倷亖乥倶乮倶2亅侾乯乥偲偺嫟桳揰
丂丂偺屄悢傪媮傔傛丅
乮夝乯丂俀嬋慄偺僌儔僼傪昤偔偲丄
丂丂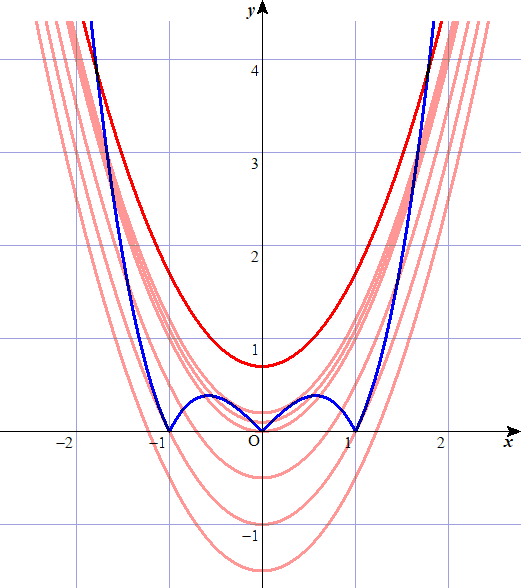
丂嬋慄 倷亖乥倶乮倶2亅侾乯乥偺僌儔僼偼丄倷 幉偵娭偟偰懳徧偱偁傞丅
丂倷亖倶2亄倠 偲嬋慄 倷亖倶乮倶2亅侾乯偑愙偡傞偲偒丄丂倶3亅倶2亅倶亖倠
丂倷亖倶3亅倶2亅倶丂偲偍偔偲丄倷乫亖俁倶2亅俀倶亅侾亖乮俁倶亄侾乯乮倶亅侾乯亖侽丂傛傝丄倶亖亅侾/俁丄侾
丂倶亖亅侾/俁丂偺偲偒丄丂倷亖俆/俀俈丂丄倶亖侾丂偺偲偒丄丂倷亖亅侾
傛偭偰丄丂倠亖俆/俀俈丂偺偲偒丄倷亖倶2亄倠 偲嬋慄 倷亖倶乮倶2亅侾乯偑愙偡傞丅
丂偙偺偲偒偺愙揰偼丄乮亅侾/俁丆俉/俀俈乯
丂倠亖亅侾丂偺偲偒丄倷亖倶2亄倠 偲嬋慄 倷亖倶乮倶2亅侾乯偑愙偡傞丅
丂偙偺偲偒偺愙揰偼丄乮亅侾丆侽乯
丂埲忋偐傜丄曻暔慄 倷亖倶2亄倠 偲嬋慄 倷亖乥倶乮倶2亅侾乯乥偲偺嫟桳揰偺屄悢偼丄
丂倠亙亅侾丂偺偲偒丄丂侽屄
丂倠亖亅侾丂偺偲偒丄丂俀屄
丂亅侾亙倠亙侽丂偺偲偒丄丂係屄
丂倠亖侽丂偺偲偒丄丂俆屄
丂侽亙倠亙俆/俀俈丂偺偲偒丄丂俇屄
丂倠亖俆/俀俈丂偺偲偒丄丂係屄
丂倠亜俆/俀俈丂偺偲偒丄丂俀屄丂丂乮廔乯
乮僐儊儞僩乯丂僌儔僼傪偟偭偐傝昤偐側偄偲丄戝曄尩偟偄栤戣偱偡偹丅
乮捛婰乯丂椷榓俈擭侾侽寧俁擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮俀侽侽侽乯偺栤戣偼丄抧摴偵応崌暘偗偡傞栤戣偱偁傞丅
栤戣丂丂|倶2亅俁倶亄侾|亜 |倶2亅侾|亅|俀倶亅侾| 傪枮偨偡 倶 偺斖埻傪媮傔傛丅
乮夝乯丂倶2亅俁倶亄侾亖侽丂傪夝偄偰丄丂倶亖乮俁亇 乯/俀
乯/俀
丂倶2亅侾亖侽丂傪夝偄偰丄丂倶亖亇侾
丂俀倶亅侾亖侽丂傪夝偄偰丄丂倶亖侾/俀
丂偙偺偲偒丄丂亅1亙乮俁亅 乯/俀亙侾/俀亙侾亙乮俁亄
乯/俀亙侾/俀亙侾亙乮俁亄 乯/俀丂偱偁傞丅
乯/俀丂偱偁傞丅
丂倶亙亅侾丂偺偲偒丄丂倶2亅俁倶亄侾亜倶2亅侾亄俀倶亅侾 偐傜丄俆倶亅俁亙侽丂傛傝丄丂倶亙俁/俆
丂丂傛偭偰丄丂倶亙亅侾
丂亅1亝倶亙乮俁亅 乯/俀丂偺偲偒丄倶2亅俁倶亄侾亜亅倶2亄侾亄俀倶亅侾 偐傜丄俀倶2亅俆倶亄侾亜侽
乯/俀丂偺偲偒丄倶2亅俁倶亄侾亜亅倶2亄侾亄俀倶亅侾 偐傜丄俀倶2亅俆倶亄侾亜侽
丂丂傛偭偰丄丂亅侾亝倶亙乮俆亅 乯/係
乯/係
丂乮俁亅 乯/俀亝倶亙侾/俀丂偺偲偒丄丂亅倶2亄俁倶亅侾亜亅倶2亄侾亄俀倶亅侾 偐傜丄丂倶亜侾
乯/俀亝倶亙侾/俀丂偺偲偒丄丂亅倶2亄俁倶亅侾亜亅倶2亄侾亄俀倶亅侾 偐傜丄丂倶亜侾
丂丂傛偭偰丄夝側偟
丂侾/俀亝倶亙侾丂偺偲偒丄丂亅倶2亄俁倶亅侾亜亅倶2亄侾亅俀倶亄侾 偐傜丄丂倶亜俁/俆
丂丂傛偭偰丄丂俁/俆亙倶亙侾
丂侾亝倶亙乮俁亄 乯/俀丂偺偲偒丄丂亅倶2亄俁倶亅侾亜倶2亅侾亅俀倶亄侾 偐傜丄俀倶2亅俆倶亄侾亙侽
乯/俀丂偺偲偒丄丂亅倶2亄俁倶亅侾亜倶2亅侾亅俀倶亄侾 偐傜丄俀倶2亅俆倶亄侾亙侽
丂丂傛偭偰丄丂侾亝倶亙乮俆亄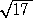 乯/係
乯/係
丂乮俁亄 乯/俀亝倶丂偺偲偒丄丂倶2亅俁倶亄侾亜倶2亅侾亅俀倶亄侾 偐傜丄丂倶亙侾
乯/俀亝倶丂偺偲偒丄丂倶2亅俁倶亄侾亜倶2亅侾亅俀倶亄侾 偐傜丄丂倶亙侾
丂丂傛偭偰丄夝側偟
丂埲忋偐傜丄媮傔傞夝偼丄丂倶亙乮俆亅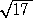 乯/係丂丄俁/俆亙倶亙乮俆亄
乯/係丂丄俁/俆亙倶亙乮俆亄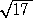 乯/係丂丂乮廔乯
乯/係丂丂乮廔乯
丂丂埲壓丄岺帠拞両







 丂
丂



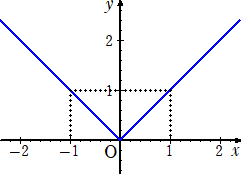


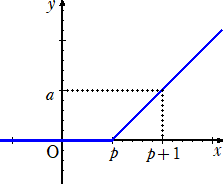


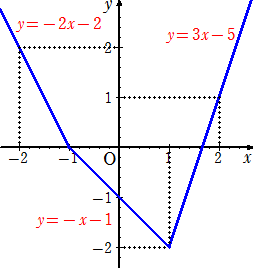


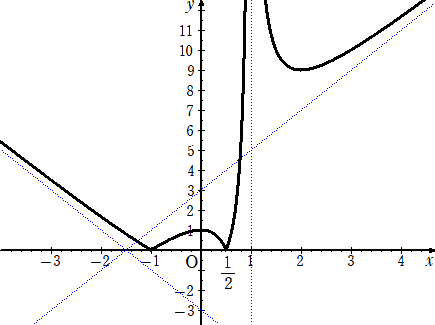 丂丂乮廔乯
丂丂乮廔乯



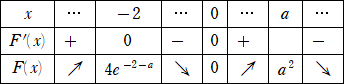
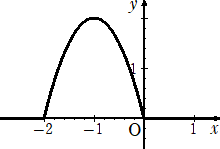
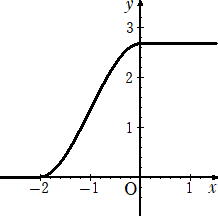

 丂丂乮廔乯
丂丂乮廔乯