グラフ理論の面白さ 
私の大学院時代、グラフ理論を専攻されている方が隣の研究室にいられた。ときどき遊び
に行くと、黒板に何やら「絵」が書いてあって、計算をされていた。今まで出会ったこともない
計算に新鮮さを感じた。私自身、当時、解析的な代数幾何学を専攻していて、他の分野の
数学を勉強する余裕もなく、ただ、「私のやっている数学と少し違う?」という感覚だけが記
憶に残った。
TVなどの教養番組などで、秋山 仁 先生が楽しそうに、グラフ理論に関わる問題を解説
されているのを見ると、思わず「勉強してみようかな!」という気になってしまう。根上生也先
生の書かれた「グラフ理論3段階」(遊星社)という本が、初心者にも分かりやすく、グラフ理
論を解説していると思う。
グラフ理論は情報科学と関係があるということで、近年注目されている数学の分野である。
このページでは、いくつかの例題を通して、グラフ理論の面白さを体験したいと思う。
ところで、グラフ理論でいう「グラフ」というのは、多分一般の方が思い浮かべる「グラフ」と
は違う。それは、点(グラフ理論では、頂点)と線(グラフ理論では、辺)で構成される。グラ
フ理論では、次の「ペテルセン・グラフ」が、最も美しいグラフといわれる。
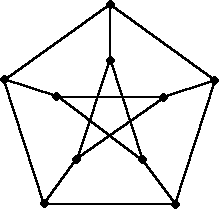
このようなグラフを使った問題を考えてみよう。
問題 平面上に、点が9個ある。点の間を何本かの直線で結ぶ。このとき、どのような直線
の引き方をしても、点から出る直線の本数が等しい点が、少なくとも2つあることを示
せ。
まず、適当に点同士を直線で結んでみよう。
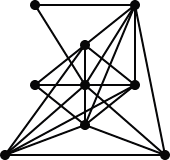 |
このとき、点から出る直線の本数が、
5本のもの ・・・・ 3点ある
6本のもの ・・・・ 2点ある
ということが分かる。
他の引き方をしたら、「直線の本数が全て異なるようにでき
るんじゃない?」という人がいるかもしれないが、実は、それ
は絶対に不可能であることが、次のようにして示される。
|
(解) 各点から出る直線の本数の可能性は、0〜8 の何れかである。このとき、点から出る
直線の本数が 0 の点と、8 の点は、同一のグラフ上で同時に存在しえない。
従って、各点から出る直線の数は、8通りある。
しかるに、点は、9 個あるので、鳩ノ巣原理により、少なくとも2点で、点から出る直線の
本数は等しい。 (終)
解答から分かるように、この事実は、点が何個あっても成り立つ。
問題 平面上に、点が6個あり、1から6までの番号が付けられている。任意の2点同士、直
線で結ばれているか、いないかのどちらかである。
このとき、少なくとも3点が、互いに直線で結ばれているか、全く直線で結ばれていな
いかの何れかが成り立つ。
(解) 任意の2点同士、直線で結ばれているか、いないかのどちらかであるので、それらを
線分の色(2色)で表すことにする。番号1の点で考えても、一般性は失わない。
番号1の点と他の5点が直線で結ばれている、いないを左図のように2色の線分で表
|
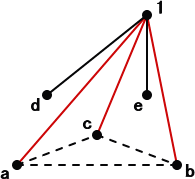 |
すと、必ず、ある1色の線分が少なくとも3本ある。その3本
の線分で結ばれた3点を、a、b、c とおく。
a と b 、b と c 、c と a を結ぶ線分の何れかが、番号1と
結ばれた線分と同色なら、題意は満たされる。
a と b 、b と c 、c と a を結ぶ線分のどれもが、番号1 と
結ばれた線分と異なる色なら、題意は満たされる。 (終) |
このような考え方は、数学に限らず実生活でも、いろいろ応用ができそうだ。
(応用例)
1.平面上にどの3点も一直線上にない6点がある。任意の2点を赤または青の線で結ぶと
き、必ず同色の線分で囲まれた三角形が存在する。(ラムゼーの定理)
このラムゼーの定理は、 点の数が5個の場合は、成り立たない。
実際に、各頂点に接続する同色の辺が2本ずつになるように配置できるからである。
点の数が7個以上の場合はもちろん成立する。
実際に、7個の頂点から任意に6点を選んで、その6点を結ぶ辺だけに着目すればよい。
2.6人の集団の中で、必ず顔見知り同士の3人か、または互いに顔見知りではない3人が
存在する。
(参考文献:情報処理教育研究会 編 情報数学の基礎 (日本理工出版会))
「堀江伸一」さんという方が当HPの掲示板「出会いの泉」に次の問題を提起された。
(平成23年3月30日付け)
グラフ理論に関係しそうな雰囲気で面白そうなのだが、如何せん、私の知らない分野なの
で、勉強しながらまとめていきたいと思う。
問 題 ある電気の全く通ってない発展途上国で、発電所を作り電力を流すことになった。
電気を必要とする地点は n 点あるが、元の発電所の能力が低いため全部に流すこ
とはできない。病院などの優先度の高い地点にだけ電気を通すことになった。地点
には、0 〜 n−1 までの番号が付けられ、各地点は離れていて何本かの道路でつ
ながっている。電線は、全て道路にそって敷設されることとなった。(地点と道路はグ
ラフの関係になっています。)
以下の情報が与えられるものとする。
・道路がつながっている2地点の番号とその距離
・電気を送りたい地点の数 m と、どの地点なのかを表す各地点の番号が m 個
・発電所のある地点の番号
指定されたm個の地点全てに電気を流す必要があります。発電所から到達できない地点
はないと仮定して、敷設する電線の長さの総計が最小になるアルゴリズム(または考え方)
を求めてください。
(補足) 電気を通さない n−m 個の点については、電線の単なる通路として利用してよい。
この問題の解き方を、「C# と VB.NET の質問掲示板」で質問したところ、線形ロゴウス
キー法という方法で解ける、というヒントを頂きました。が、リンク先掲示板ではきちんとし
た回答が頂けずじまいです。線形ロゴウスキー法やこの問題について詳しい方、考え方
の概論などをお願いします
(→ 参考) 堀江伸一さんの投稿記事(平成23年3月31日付け)
HN「通りすがり」さんが、参考文献をあげられました。(平成23年3月31日付け)
・最短シュタイナー問題(フェルマー(Fermat)点、シュタイナー(Steiner)点)
・最小シュタイナー木(トリチェリの作図法、Melzak のアルゴリズム)
・Steiner最小木問題の初等幾何的取り扱い
(参考) シュタイナー問題とは、
平面上にn個の点 P1、P2、・・・、Pn が与えられたとき、これらを線分で結ぶ最短ネット
ワークを作れ。
ただし、このときに任意の個数の点 Q1、Q2、・・・、Qm を任意の位置に付け加えてよい。
・トリチェリの問題
・最小全域木問題・・・クラスカル(Kruskal)とプリム(Prim)のアルゴリズム
「堀江伸一」さんからのコメントです。(平成23年4月1日付け)
上記の問題は、一般の重み付きグラフの解法についてのものです。地点と地点を繋げて
いる道路がまっすぐでなく、山道のようにカーブがたくさんある場合を考慮しなければなりま
せん。
at さんからのコメントです。(平成23年4月2日付け)
一般のグラフの問題においても、「最小シュタイナー木問題」というものがあるようです。
「最小シュタイナー木問題」はNP困難であることが知られているようです。
「堀江伸一」さんからのコメントです。(平成23年4月5日付け)
グラフに対する最小シュタイナー木も、平面でのシュタイナー木も遺伝的アルゴリズムの
ような賢い方法ならまあまあの答えで解けるのでしょうね。遺伝的アルゴリズムって難しそ
うですね。
こちらのサイトに、シュタイナー木を解くアルゴリズムがありましたが、解説が簡潔すぎて
全くメージできませんでした。
at さんからのコメントです。(平成23年4月8日付け)
Dreyfus-Wagner のアルゴリズムは、「最小シュタイナー木はいくつかの最小シュタイナ
ー木に分解できる」という性質を使っているのですね。Dreyfus-Wagner
のアルゴリズム
をさらに詳しく解説してある日本語で書かれた本を一冊挙げておきます。
B・コルテ/J・フィーゲン 著 「組合せ最適化 理論とアルゴリズム」
(シュプリンガー・フェアラーク東京)
この本の第20章に、Dreyfus-Wagner アルゴリズムについての説明があります。かな
り丁寧に書かれてあります。最小シュタイナー木問題がNP困難問題であることの証明も載
っています。
この本の原書は、「Combinatorial Optimization Theory and Algorithms」です。英文の本
です。現在、この本の全内容を無料でダウンロードして閲覧することができます。
上記の文献を参考に、最短ネットワーク問題の基礎の基礎をまとめていこう。
最短ネットワーク問題とは、
平面上の n 個全ての点を結ぶ経路のうち長さが最短であるものを求める問題
である。経路としては、2点を結ぶ線分はもちろん、n 個の点とは異なる中継点を経由する
線分が考えられる。
例 平面上に1辺の長さが1の正三角形 ABC がある。
(1) 辺だけを経由する場合
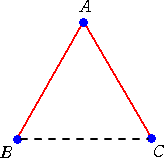 この場合、3点A、B、C は辺AB、ACで結ばれ、長さは2である。
この場合、3点A、B、C は辺AB、ACで結ばれ、長さは2である。
このように、与えられた点だけで得られる最短ネットワークを
最小木という。
(2) 重心を経由する場合
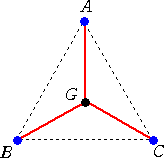 この場合、3点A、B、C は重心Gと結ばれ、長さは
この場合、3点A、B、C は重心Gと結ばれ、長さは となるが、
となるが、
この長さは、上記の最小木の場合より短く、3点が与えられた場
合の最短ネットワークとなる。
このように、与えられた点の他に任意個数の中継点を付加し
て得られる最短ネットワークを最小シュタイナー木といい、付
加される点をシュタイナー点という。
上記では、正三角形の3頂点という特殊な点であるが、一般に、
平面上の3点からの距離の総和が最小となる点を求めよ
という Fermat の問題(17世紀頃)が古くから知られ、Torricelli、Cavalieri、Simpson
らの先人達が解決してきている。
また、この問題は「平面上の n 個の点」に拡張され、Jakob Steiner(17961〜863)によ
り解決されている。
例 平面上の適切な位置にある4点を結ぶ最小シュタイナー木を作図せよ。
(作図方法)
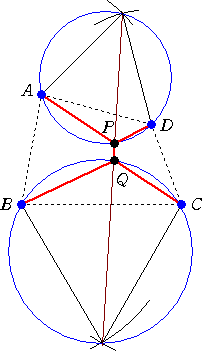 |
1.四角形ABCDの2辺AD、BCを1辺とする正三角形
をそれぞれ作図する。
2.1.で作図した正三角形の外接円をそれぞれ作図す
る。
3.A、B、C、Dとは異なる2つの正三角形の頂点同士
を結び、外接円との交点をそれぞれP、Qとする。
4.左図のように、6点A、B、C、D、P、Qを結んだもの
を考えればよい。 |
もちろん、次のような作図も考えられる。
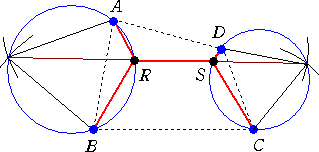
2つのネットワークの距離を比較すれば、図から明らかなように後者の方が距離が短い。
したがって、4点が上図のように配置されている場合、後者が最小シュタイナー木を与え
る。(もちろん、前者か後者かは、そのときの4点の配置で定まる。)このとき、2点R、Sが、
シュタイナー点となる。
上記の(作図方法)では、次の事実が用いられている。
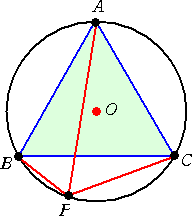
正三角形ABCの外接円Oの弧BC上のどんな点P
についても、
AP=BP+CP
が成り立つ。
| (証明) PCの延長上に、BP=CQ となる点Qをとる。 △ABPと△ACQにおいて、 |
 |
AB=AC 、BP=CQ 、∠ABP=∠ACQ
よって、△ABP≡△ACQ となり、 AP=AQ
∠APQ=60°より、∠AQP=60°
したがって、△APQは正三角形となり、
AP=PQ=BP+CP が成り立つ。 (証終) |
(コメント) この事実は、高校の教科書にも載っているくらい有名なものであるが、まさか「最
小シュタイナー木」の問題に関連しているとは微塵にも思わなかった。あらためて、
平面幾何の奥深さを実感した。
また、上記の証明では、正三角形を強引に作った感は否めないが、プトレマイオスの定理
を用いた、ごく自然な証明も知られている。
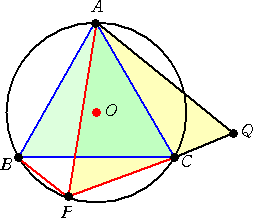
(別証) 四角形ABPCは円Oに内接するので、プトレマイオスの定理より、
AP・BC=BP・AC+CP・AB
△ABCは正三角形なので、 BC=AC=AB より、
AP=BP+CP が成り立つ。 (別証終)
平面上に3点A、B、Cがある。△ABCの内角は全て120°未満とする。
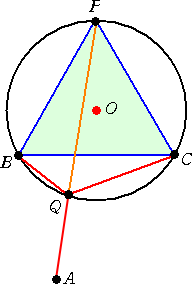 このとき、辺BCに関して、Aと反対側に点Pを、△PBCが
このとき、辺BCに関して、Aと反対側に点Pを、△PBCが
正三角形であるようにとる。△PBCの外接円Oと線分APと
の交点をQとする。
2点A、Pを結ぶ線分が最短の距離を与える。
また、上記の事実から、AQ+PQ=AQ+BQ+CQ で
長さが最小になるのは、Qが線分AP上にあるときである。
したがって、平面上の適切な3点に対して、左図が最小
シュタイナー木を与え、点Qがシュタイナー点となる。
上記のような作図法を、「トリチェリの作図法」という。この作図法により、2点B、Cがあ
たかも1点Pに代替されることが分かる。
すなわち、「3点からの距離の和が最小」という問題が、「2点からの距離の和が最小」と
いう問題に簡約される。
この「トリチェリの作図法」を活用する、最短ネットワーク問題を解くアルゴリズムとして、メ
ルザク(Melzak)のアルゴリズムが知られている。
例 次の点の配置に対して、メルザクのアルゴリズムを適用してみよう。

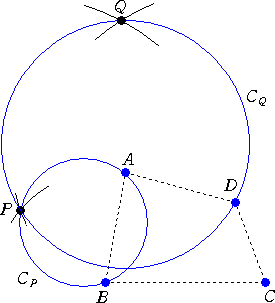
1.4点A、B、C、D の中から3点A、B、Dを選ぶ。この3点に「トリチェリの作図法」を適用
して、AとBの代替点P、外接円CPを求める。
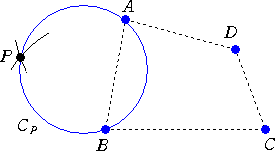
2.3点P、C、D に「トリチェリの作図法」を適用して、PとDの代替点Q、外接円CQを求め
る。
3. 線分CQと円CQの交点Kを求め、さらに、線分KPと円CPの交点Hを求める。
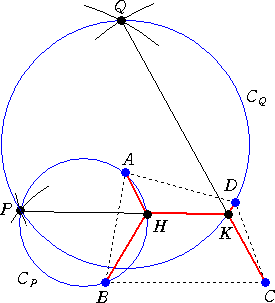
上図において、 CQ=CK+KQ=CK+(KD+KP)
=CK+KD+KH+HP=CK+KD+KH+(HA+HB)
より、 AH+BH+HK+CK+DK=CQ である。
このようにして、4点A、B、C、Dに対する一つのシュタイナー木が求められる。
ただ、このネットワークが最短かどうかは分からない。点の選び方により、多くのネットワ
ークが得られ、その中から最小シュタイナー木を探すことになる。その場合の数は点の個
数が増えると甚大になる!
例 正5角形の頂点A、B、C、D、E に対して、メルザクのアルゴリズムを適用してみよう。
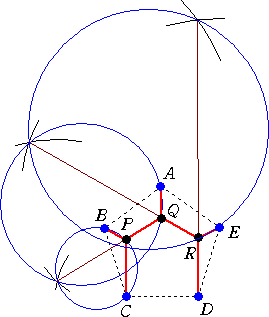
「トリチェリの作図法」では、内角の大きさが全て120°未満という制約があった。それで
は、正6角形の頂点A、B、C、D、E、F に対して、メルザクのアルゴリズムを適用してみたら
どんな事件が起こるのだろうか?
実際に作図してみた。
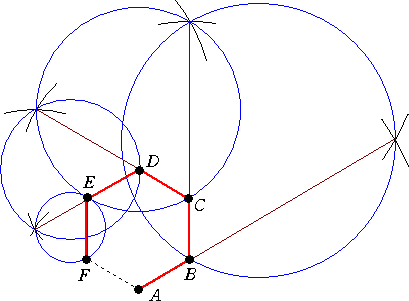
ネットワークが辺だけで構成されるようになるんですね!
実は、次の事実が知られているらしい。
定 理 正 n 角形(n≧6)の頂点に対する最小シュタイナー木は、正 n 角形から
任意の一辺を取り除いたものである。
(コメント) この定理の結果は、ちょっと肩すかしかな?
(追記) Dengan kesaktian Indukmu さんからご投稿いただきました。(令和4年6月3日付け)
シュタイナー点について面白そうでしたので、気がついたことを投稿させて頂きます。
上記の再掲です。
例 平面上の適切な位置にある4点を結ぶ最小シュタイナー木を作図せよ。

(作図方法)
 |
1.四角形ABCDの2辺AD、BCを1辺とする正三角形
をそれぞれ作図する。
2.1.で作図した正三角形の外接円をそれぞれ作図す
る。
3.A、B、C、Dとは異なる2つの正三角形の頂点同士
を結び、外接円との交点をそれぞれP、Qとする。
4.左図のように、6点A、B、C、D、P、Qを結んだもの
を考えればよい。 |
さて、ADを1辺とする正三角形を△ADX、BCを1辺とする正三角形を△BCYと呼ぶことと
します。上記の3.の「A、B、C、Dとは異なる2つの正三角形の頂点同士を結び」とあるのは、
「X、Yを結び、」と同じ意味となります。
このときに、
線分XPの長さは、線分APの長さに線分DPの長さを加えたものと等しく、
線分YQの長さは、線分BQの長さに線分CQの長さを加えたものと等しくなっているので
すね!!
・・・・・・・・・・・・・・これを「性質1」と呼ぶこととします。
P、Qの位置の定義によれば、2点ともに直線XY上にあるわけですが、この条件をいったん
はずして、点Pは弧ADの上をふらふらと動き、点Qは弧BCの上をふらふらと動くものとします
と、4点A、B、C、Dを結ぶ木の全長は、折れ線、XPQYの全長と等しいわけです。
これには性質1を使っています。
この折れ線の全長が最短となるのは、直線XY上に、点P,点Qが存在するときとなります。
同時に、
4点A、B、C、Dを結ぶ最小シュタイナー木の【候補】がひとつ作図できたことになります。
もうひとつの候補も作図して、どちらのほうが最短になるか比較することになりますが……
以上は、∠APDや∠BQCが120°などを使っていませんが、面白いと思いました。
以下、工事中!




 この場合、3点A、B、C は辺AB、ACで結ばれ、長さは2である。
この場合、3点A、B、C は辺AB、ACで結ばれ、長さは2である。 この場合、3点A、B、C は重心Gと結ばれ、長さは
この場合、3点A、B、C は重心Gと結ばれ、長さは




 このとき、辺BCに関して、Aと反対側に点Pを、△PBCが
このとき、辺BCに関して、Aと反対側に点Pを、△PBCが



