トリチェリの問題　　　　　　　　　　　　　　　　　　　　　　

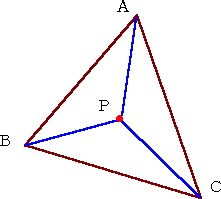
任意の鋭角三角形ＡＢＣ の内部の点Ｐに対して、 　　　　　　ＰＡ＋ＰＢ＋ＰＣ 　が最小となる点Ｐを作図せよ。 　　この問題は、フェルマーがトリチェリに出題したといわ 　れる。 　　そのため、この問題は正式には「フェルマーの問題」 　と言われるようだ。

　さらに、上記の三角形は、１２０°を超えない内角を持つ三角形に拡張され、点Ｐのことを、
Ｆｅｒｍａｔ　ｐｏｉｎｔ　と言うそうだ。

　トリチェリにより、いくつかの解法が知られている。

点Ｐの作図のために、次の定理が用いられる。

ヴィヴィアーニ（Ｖｉｖｉａｎｉ）の定理

　正三角形ＡＢＣ の内部の任意の点Ｐに対して、点Ｐより各辺に下ろした垂線の長さ
の和は一定で、正三角形の高さに等しい。

　証明は、中学レベルで可能だろう。

　正三角形において、重心と垂心は一致するので、重心から正三角形の各辺に下ろした垂
線の長さは、正三角形の高さの１/３で、その長さを３つ合わせれば、正三角形の高さに一
致する。重心に限らず、正三角形の内部の任意の点でも、やはり、その長さの和は正三角
形の高さに等しいことを主張する定理が、ヴィヴィアーニの定理である。

（証）　△ＡＢＣ＝△ＰＡＢ＋△ＰＢＣ＋△ＰＣＡ より、明らか。　（終）

　任意の鋭角三角形に外接する正三角形がうまく作図できれば、ヴィヴィアーニの定理に
より、トリチェリの問題は解決される。

作図の方法　　下図において、△ＡＢＣ が任意に与えられた鋭角三角形とする。



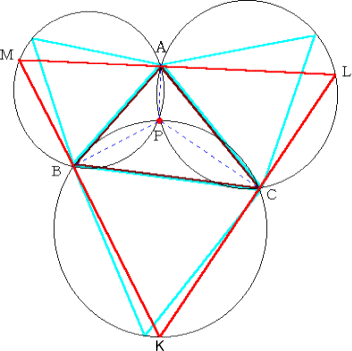　（１）　△ＡＢＣ の各辺を一辺とする

　　　正三角形（水色）を作図する。

　（２）　各正三角形の外接円を作図

　　　する。

　（３）　３円の交点Pが求める点であ
　　　る。


　∠ＡＰＢ＝∠ＢＰＣ＝∠ＣＰＡ＝120°

から、上記の点Ｐがただ一つ定まる

ことは明らかだろう。




　作図した点P が求める点であることを示すために、上図のような正三角形ＫＬＭ（赤色）

を作図する。

　正三角形の各辺は、それぞれＰＡ、ＰＢ、ＰＣに対して垂直であるようにできる。

　点Ｑを△ＡＢＣ の内部の任意の点とする。このとき、明らかに、ＱＡ＋ＱＢ＋ＱＣの値は、

点Ｑより正三角形ＫＬＭの各辺に下ろした垂線の長さの和以上に大きい。

　ところが、ヴィヴィアーニの定理により、点Ｑより正三角形ＫＬＭの各辺に下ろした垂線

の長さの和は ＰＡ＋ＰＢ＋ＰＣ に等しい。

　よって、ＰＡ＋ＰＢ＋ＰＣ≦ＱＡ＋ＱＢ＋ＱＣ となり、作図された点Ｐが、ＱＡ＋ＱＢ＋ＱＣ

の最小値を与える点であることが分かる。


（参考文献：Ｈ．デリー 著 根上生也 訳　数学１００の勝利（シュプリンガー・フェアラーク東京））

　当ＨＰがいつもお世話になっているＳ（Ｈ）さんからの情報によれば、次のようにしても作
図できるようだ。

　すなわち、正三角形の頂点と、正三角形の１辺の対角の頂点を結ぶ線分の交点として
作図される。（証明は円周角の定理より明らかだろう。）

　　　　　　　　

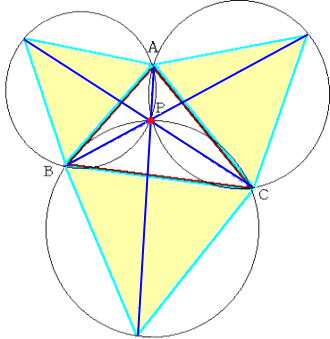
　また、次のような図と睨めっこしても上図のことは了解できるだろう。Ｓ（Ｈ）さんよりご教示
いただきました。Ｓ（Ｈ）さんに感謝します。

　　　　　　　　

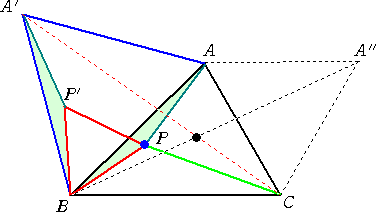
　△ＡＢＣの内部の点Ｐに対し、△ＢＰＰ’が正三角形になるように取る。

　ＡＢを１辺とする正三角形の他の頂点をＡ’、ＡＣを１辺とする正三角形の他の頂点をＡ”と
する。

　このとき、　ＰＡ＋ＰＢ＋ＰＣ＝Ａ’Ｐ’＋Ｐ’Ｐ＋ＰＣ≧Ａ’Ｃ　なので、ＰＡ＋ＰＢ＋ＰＣが最小と

なる点Ｐは、線分Ａ’Ｃ上にある。

　同様にして、ＰＡ＋ＰＢ＋ＰＣが最小となる点Ｐは、線分Ａ”Ｂ上にある。

　以上から、求める点Ｐは、線分Ａ’Ｃと線分Ａ”Ｂの交点として作図される。