 丂
丂丂巐妏宍偺偆偪偱丄堦慻偺懳曈偑暯峴側傕偺偑戜宍偱偁傞丅
戜宍偺惈幙丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂
丂
丂巐妏宍偺偆偪偱丄堦慻偺懳曈偑暯峴側傕偺偑戜宍偱偁傞丅
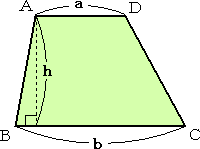 |
丂丂丂戜宍偺柺愊 俽 偺岞幃偲偟偰師偑抦傜傟偰偄傞丅 丂丂丂 丂丂亀丂乮忋掙亄壓掙乯亊崅偝亐俀丂亁偲丄偦傜傫偠偰偍傜傟傞 丂曽傕懡偄偩傠偆丅 |
丂嫵壢彂摍偱偼丄捠忢丄師偺傛偆側宍偱愢柧偝傟偰偄傞丅
丂摨偠戜宍傪俀偮梡堄偟丄壓恾偺傛偆偵慻傒崌傢偣偰暯峴巐曈宍傪嶌傞丅
丂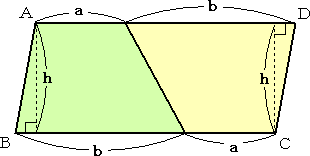
丂暯峴巐曈宍偺柺愊偺岞幃偐傜丄俀俽亖乮倎亄倐乯倛
傛偭偰丄
丂![]()
丂崱傑偱丄
丂![]()
偺晹暘偺棟夝傪忋婰偺傛偆偵峫偊丄偁傑傝怺擖傝偟偰峫偊傞偙偲偼側偐偭偨偑丄嵟嬤丄堎側
傞棟夝偑偁傞偙偲傪抦傞婡夛偑偁偭偨丅
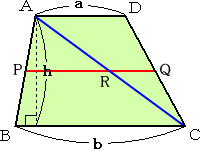 |
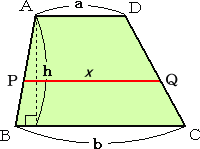
丂丂嵍恾偵偍偄偰丄俀揰 俹丄俻 偼丄偦傟偧傟俙俛丄俠俢偺拞揰 丂偱偁傞丅慄暘俙俠偲慄暘俹俻偺岎揰傪丄俼偲偡傞丅偙偺偲偒丄 丂仮俙俛俠偵偍偄偰丄拞揰楢寢偺掕棟傛傝丄俛俠亖俀俹俼丂偱 丂偁傞丅仮俙俠俢偵偍偄偰傕摨條偵偟偰丄俙俢亖俀俻俼丂偱偁傞丅 |
丂偟偨偑偭偰丄丂俙俢亄俛俠亖俀俻俼亄俀俹俼亖俀俹俻丂傛傝丄丂俹俻亖乮俙俢亄俛俠乯/俀
| 丂丂偡側傢偪丄俹俻亖 | 丂偑惉傝棫偮丅 |
丂偙偺偙偲偐傜丄戜宍偺柺愊傪媮傔傞応崌偵師偺傛偆側媮傔曽傕偁傞偲偄偆偙偲偱偁傞丅
戜宍傪丄暯峴慄偵増偭偰恑傓摴偲峫偊丄
丂乮戜宍偺柺愊乯亖乮摴偺拞墰慄偺挿偝乯亊乮摴暆乯
偙偺偙偲偼丄師偺恾傪尒傟偽柧傜偐偩傠偆丅
丂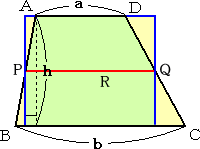
丂偝偰丄忋婰偺傛偆偵丄拞墰慄偺挿偝偐傜戜宍偺柺愊傪媮傔傜傟傞栿偩偑丄偙偺拞墰慄偼
摉慠側偑傜戜宍偺柺愊傪摍暘偵暘偗偰偼偄側偄丅
 |
丂丂嵍恾偺傛偆偵丄俙俢 偵暯峴側慄暘 俹俻 偱丄戜宍偺柺愊偑 丂摍暘偝傟傞偲偒丄俁偮偺悢 倎 丄倐 丄倶 偵偼丄偳偺傛偆側娭學 丂幃偑惉傝棫偮偺偩傠偆偐丠 丂丂偙偺栤偄偐偗偵懳偟偰丄崅峑侾擭偺乽悢妛嘥乿偱妛廗偡傞 丂乽柺愊斾偼憡帡斾偺俀忔偵摍偟偄乿 丂偲偄偆帠幚傪梡偄傟偽夝寛偝傟傞丅 丂乮仺丂嶲峫 丗 憡帡斾偺恀幚丂乯 |
| 丂塃恾偵偍偄偰丄仮俤俙俢佷仮俤俹俻佷仮俤俛俠丂偱丄 憡帡斾偼丄丂倎 丗 倶 丗 倐丂傛傝丄 丂仮俤俙俢 丗 仮俤俹俻 丗 仮俤俛俠亖倎2 丗 倶2 丗 倐2 偑惉傝棫偮丅 丂傛偭偰丄丂倶2 亅 倎2 亖 倐2 亅 倶2丂傛傝丄 慄暘 俹俻 偺挿偝 倶 偼丄 丂 |
丂丂丂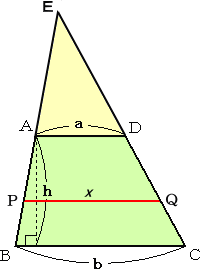 |
丂椺偊偽丄丂倎亖侾丂丄丂倐亖俈丂偺偲偒丄丂倶亖俆丂偲側傝丄俁偮偺悢 倎 丄倐
丄倶 偼丄偲傕偵帺慠悢
偲側傞丅
丂俁偮偺悢 倎 丄倐 丄倶 偑丄偲傕偵帺慠悢偵側傞応崌傪峫偊傞偙偲偼丄偲偰傕嫽枴偁傞偙偲偱偁
傞丅
丂倶2 亅 倎2 亖 倐2 亅 倶2丂傛傝丄丂倎2 亄 倐2 亖 俀倶2丂偲側傞偑丄
丂乮倱亅倲乯2亄乮倱亄倲乯2亖俀乮倱2亄倲2乯
偱偁傞偙偲傪峫偊傞偲丄丂倱2亄倲2亖倶2丂偲側傞傛偆側帺慠悢夝乮 倱 丆 倲 丆 倶 乯傪扵偣偽傛偄偙偲
偵側傞丅
丂偙傟偼丄僺僞僑儔僗悢傪媮傔傞偙偲偵摍偟偔丄
丂倱亖倣2亅値2丂丄倲亖俀倣値丂丄倶亖倣2亄値2
偲彂偐傟傞丅
丂偨偩偟丄倣丄値
偼丄屳偄偵慺側帺慠悢偱丄偳偪傜偐偼嬼悢丄偐偮丄倣亜値 偲偡傞丅
乮徻偟偔偼丄偙偪傜傪嶲徠乯
丂師偺昞偼丄僺僞僑儔僗悢傪偄偔偮偐傑偲傔偨傕偺偱偁傞丅
| 倣 | 俀 | 俁 | 係 | 係 | 俆 | 俆 | 俇 | 俇 | 俈 | 俈 | 俈 |
| 値 | 侾 | 俀 | 侾 | 俁 | 俀 | 係 | 侾 | 俆 | 俀 | 係 | 俇 |
| 倱 | 俁 | 俆 | 侾俆 | 俈 | 俀侾 | 俋 | 俁俆 | 侾侾 | 係俆 | 俁俁 | 侾俁 |
| 倲 | 係 | 侾俀 | 俉 | 俀係 | 俀侽 | 係侽 | 侾俀 | 俇侽 | 俀俉 | 俆俇 | 俉係 |
| 倶 | 俆 | 侾俁 | 侾俈 | 俀俆 | 俀俋 | 係侾 | 俁俈 | 俇侾 | 俆俁 | 俇俆 | 俉俆 |
丂偙偺昞偐傜丄俁偮偺悢 倎 丄倐 丄倶 偑丄偲傕偵帺慠悢偵側傞応崌偺昞偑摼傜傟傞丅
丂倎亖乥倱亅倲乥丂丄丂倐亖倱亄倲
| 倎 | 侾 | 俈 | 俈 | 侾俈 | 侾 | 俁侾 | 俀俁 | 係俋 | 侾俈 | 俀俁 | 俈侾 |
| 倐 | 俈 | 侾俈 | 俀俁 | 俁侾 | 係侾 | 係俋 | 係俈 | 俈侾 | 俈俁 | 俉俋 | 俋俈 |
| 倶 | 俆 | 侾俁 | 侾俈 | 俀俆 | 俀俋 | 係侾 | 俁俈 | 俇侾 | 俆俁 | 俇俆 | 俉俆 |
丂忋婰偺昞偱丄栤戣愝掕偱堘榓姶側偔巊偊傞偺偼丄乮 倎 丄倐 丄倶 乯亖乮 俈
丄侾俈 丄侾俁 乯偖傜偄偐
側丠
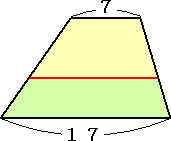 |
丂丂丂丂嵍恾偺戜宍偺柺愊傪摍暘偡傞 丂丂丂愒慄偺挿偝偼丄丂侾俁丂偱偁傞丅 |
乮捛婰乯丂暯惉侾俋擭係寧俁擔晅偗
丂忋婰偱丄戜宍偺柺愊偺岞幃偺媮傔曽傪俀偮尒偨丅巹帺恎丄戜宍偲偄偆偲丄
丂丂
偲偄偆恾偑僩儔僂儅偺傛偆偵擼棤偵偙傃傝晅偄偰偄傞丅乮彫妛俆擭惗埲棃偐側丠乯
丂嵟嬤丄師偺傛偆偵媮傔傞曽朄偑偁傞偙偲傪抦偭偨丅
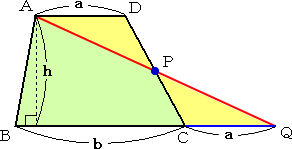 |
丂丂曈俠俢偺拞揰俹傪偲傝丄俙俹偺墑挿偲俛俠偺 丂墑挿偲偺岎揰傪俻偲偡傞丅 丂丂偙偺偲偒丄俀妏汃曈憡摉偵傛傝丄 丂丂仮俙俹俢佭仮俻俹俠 丂丂傛偭偰丄戜宍偺柺愊偼丄仮俙俛俻偺柺愊偵 丂摍偟偔丄 丂丂 |
丂柺愊寁嶼傪偡傞偲偒丄偙偺乽拞揰傪峫偊傞乿偲偄偆僥僋僯僢僋偼堄奜偵岠壥揑偱偁傞丅
丂乽暯惉嫵堢埾堳夛俀侽侽俈丂擖帋捈慜僗儁僔儍儖乿乮僼僕俿倁宯丂暯惉侾俋擭侾寧係擔曻塮乯偲偄
偆摿斣偱丄師偺傛偆側栤戣偑弌戣偝傟偨丅
 |
丂丂丂丂嵍恾偺傛偆偵丄堦晹挿曽宍偺寠偺偁偄偨挿曽 丂丂丂宍偺働乕僉偑偁傞丅 丂丂丂丂乮偙傫側働乕僉偼幚嵼偟側偄偐側丏丏丏両乯 丂丂丂丂偙偺働乕僉傪偁傞堦偮偺捈慄偵増偭偰愗傞偲丄 丂丂丂挌搙敿暘偵暘偗傜傟傞偲偄偆丅 丂丂丂丂偳偺傛偆偵愗傟偽偄偄偩傠偆偐丠 |
丂偨偩丄埮塤偵愗偭偰傕敿暘偵偼側傜側偄偺偱丄悢妛揑偵峫偊傛偆丅
丂僸儞僩偼丄挿曽宍偺懳妏慄偺岎揰傪捠傞捈慄偼丄昁偢挿曽宍偺柺愊傪俀摍暘偡傞偲偄偆
帠幚偱偁傞丅
丂偙偺偙偲偵婥偑偮偗偽丄師偺傛偆偵愗傟偽傛偄偙偲偼柧傜偐偩傠偆丅
丂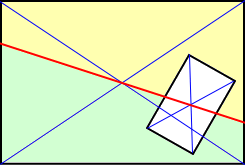
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜丄戜宍偺惈幙偵娭偡傞榖戣傪
捀偒傑偟偨丅乮暯惉俀係擭係寧侾俆擔晅偗乯
丂埲壓偺栤戣偼丄杔偑拞妛俁擭偺帪偵巊偭偰偄偨栤戣廤偺儅僀丒傾僾儘乕僠偵嵹偭偰偄偨栤
戣偱偡丅
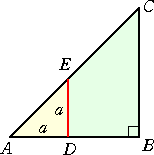 |
丂丂嵍恾偵偍偄偰丄仮ABC偼丄AB亖BC亖倶乮cm乯丄佢B=90亱偺 丂捈妏擇摍曈嶰妏宍偱偁傞丅曈俙俛丄俙俠忋偵俀揰俢丄俤傪偲傝丄 丂DE//BC丄AD亖倎乮cm乯偲偡傞丅 丂丂偙偺偲偒丄戜宍DBCE偺柺愊傪丄俀捠傝偺曽朄偱昞傢偟偰丄 丂丂丂丂倶2亅倎2亖(倶亄倎)(倶亅倎) 丂偑惉傝棫偮偙偲傪徹柧偟側偝偄丅 |
乮徹柧乯丂戜宍DBCE偺柺愊傪S偲偡傞丅DE=AD=倎乮cm乯側偺偱丄
丂S=仮ABC-仮ADE=(1/2)(AB丒BC)-(1/2)(AD丒DE)=(1/2)(倶2-倎2)丂丒丒丒丂(1)
傑偨丄戜宍DBCE傛傝丄
丂S=(1/2)(DE+BC)丒(AB-AD)=(1/2)(倶+倎)(倶-倎)丂丒丒丒丂(2)
(1)丄(2)傛傝丄丂(1/2)(倶2-倎2)=(1/2)(倶+倎)(倶-倎)丂偡側傢偪丄丂倶2-倎2=(倶+倎)(倶-倎)丂丂乮徹廔乯
丂摉帪偼慡偔暘偐傜側偐偭偨偺偱偡偑丄崱偲側偭偰偼旕忢偵傛偄栤戣偩偲巚偄傑偡丅徹柧帺
懱偼丄峴楍幃側偳偱傕偱偒傑偡丅
乮僐儊儞僩乯丂場悢暘夝偺岞幃傪婔壗揑偵偲傜偊傞偲丄報徾偵巆傝傑偡偹両