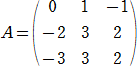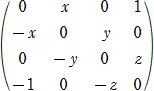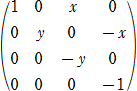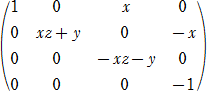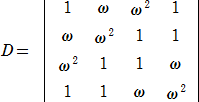数学検定に挑戦！ 　　　　　　　　　　　　　　　　　　　　　　　　

　「数学検定」は毎年３０万人ほどの方が受験される検定試験で、公益財団法人　日本数学
検定協会が運営している。問題レベルは、大体

　１級・・・大学程度　、準１級・・・高３程度　、２級・・・高２程度　、準２級・・・高１程度
　３級・・・中３程度　、４級　、・・・・・・

とされ、５級以上には、１次（計算技能）と２次（数理技能）が課され、両方合格しないと、数学
検定○級合格とはならない。

　最近、当ＨＰの読者のＭさんから、数学検定に関係するページがあればいいな〜というリク
エストがメールで寄せられた。受験料が高額なので、数学検定を受験しようとは全く思わない
が、どんな問題が出題されているか常々興味・関心があったので、ちょっと数学検定の問題
に挑戦し、その記録をまとめていきたいと思う。


問題１　次の計算をせよ。（１級１次レベル）

　　　　　　　Σ_ｐ=1〜ｎΣ_ｑ=1〜ｎ （ｐ＋ｑ）　（ただし、ｐ＞ｑ）

（解）　求める和は、

　Σ_{ｑ=1〜ｎ-1}Σ_{ｐ=2〜ｑ+1} （ｐ＋ｑ）＝(3/2)Σ_{ｑ=1〜ｎ-1}ｑ（ｑ＋１）＝（ｎ−１）ｎ（ｎ＋１）/２　　（終）

（コメント）　高校２年生程度の問題でした。


問題２　４次方程式　x⁴−４x−１＝０ について、次の問いに答えよ。（１級１次レベル）

　　（１）　上の方程式の実数解を求めよ。
　　（２）　上の方程式の虚数解を求めよ。

（解）（１）　x⁴＝４x＋１　の両辺に、２ｘ²＋１　を加えて、　x⁴＋２ｘ²＋１＝２ｘ²＋４x＋２

　　　　　すなわち、　（ｘ²＋１）²＝２（x＋１）²　となり、次のように因数分解される。

　　　　　　（ｘ²＋１＋（x＋１））（ｘ²＋１−（x＋１））＝０

　　　　　実数解は、２次方程式　ｘ²＋１−（x＋１）＝０　の解。

　　　　　よって、解の公式により、　ｘ＝（±√（４−２））/２

　　（２）　虚数解は、２次方程式　ｘ²＋１＋（x＋１）＝０　の解。

　　　　　よって、解の公式により、　ｘ＝（−±ｉ・√（４＋２））/２　　（終）

（コメント）　高校２年生程度の問題でした。

　類題　次の方程式　ｘ⁴−４ｘ³＋ｘ²−３＝０　を解きなさい。（１級１次レベル）

　因数分解出来なそうな雰囲気だが、次のような変形はすぐ思いつくだろう。

（解）　与式より、　ｘ⁴＋ｘ²＋１＝４ｘ³＋４＝４（ｘ³＋１）＝４（ｘ＋１）（ｘ²−ｘ＋１）

　　　ここで、　ｘ⁴＋ｘ²＋１＝（ｘ²＋１）²−ｘ²＝（ｘ²−ｘ＋１）（ｘ²＋ｘ＋１）　なので、

　　　　（ｘ²−ｘ＋１）（ｘ²＋ｘ＋１）＝４（ｘ＋１）（ｘ²−ｘ＋１）

　　　すなわち、　（ｘ²−ｘ＋１）（ｘ²−３ｘ−３）＝０　を解いて、

　　　　ｘ＝（１±ｉ）/２　、（３±√２１）/２　　（終）

（コメント）　高校２年生程度の問題でした。


　よおすけさんから、準１級１次レベルの問題を頂きました。（平成２７年２月７日付け）

　類題　整式　ｘ⁸＋ｘ⁴＋１　を整式　ｘ²＋ｘ＋１　で割ったときの商を求めなさい。

（解）　ｘ⁸＋ｘ⁴＋１＝ｘ⁸＋２ｘ⁴＋１−ｘ⁴

　　　　　　　　　　　＝（ｘ⁴＋１）²−ｘ⁴

　　　　　　　　　　　＝（ｘ⁴＋ｘ²＋１）（ｘ⁴−ｘ²＋１）

　　　　　　　　　　　＝（ｘ²−ｘ＋１）（ｘ²＋ｘ＋１）（ｘ⁴−ｘ²＋１）

　　よって、求める商は、　（ｘ²−ｘ＋１）（ｘ⁴−ｘ²＋１）＝ｘ⁶−ｘ⁵＋ｘ³−ｘ＋１　　（終）

（よおすけさんからのコメント）　僕が解いたときは、直接筆算でやりましたが、私の備忘録
　　　　　　　　　　　　　　　　　　「ωの真実」に載っているやり方もありかな・・・って。

　実際に、ωを用いて解いてみました。

　　　Ｆ（ｘ）＝ｘ⁸＋ｘ⁴＋１　とおくと、　Ｆ（ω）＝ω⁸＋ω⁴＋１＝ω²＋ω＋１＝０

　　同様に、Ｆ（ω²）＝ω¹⁶＋ω⁸＋１＝ω²＋ω＋１＝０

　　よって、　Ｆ（ｘ）は、　（ｘ−ω）（ｘ−ω²）＝ｘ²＋ｘ＋１　で割り切れる。

　　このとき、　ｘ⁸＋ｘ⁴＋１＝（ｘ²＋ｘ＋１）（ｘ⁶＋ａｘ⁵＋ｂｘ⁴＋ｃｘ³＋ｄｘ²＋ｅｘ＋１）　とおくと、

　　　右辺＝ｘ⁸＋ａｘ⁷＋ｂｘ⁶＋ｃｘ⁵＋ｄｘ⁴＋ｅｘ³＋ｘ²
　　　　　　　　　＋ｘ⁷＋ａｘ⁶＋ｂｘ⁵＋ｃｘ⁴＋ｄｘ³＋ｅｘ²＋ｘ
　　　　　　　　　　　　＋ｘ⁶＋ａｘ⁵＋ｂｘ⁴＋ｃｘ³＋ｄｘ²＋ｅｘ＋１

　　　　　＝ｘ⁸＋（ａ＋１）ｘ⁷＋（ａ＋ｂ＋１）ｘ⁶＋（ａ＋ｂ＋ｃ）ｘ⁵＋（ｂ＋ｃ＋ｄ）ｘ⁴
　　　　　　　　　　　　　　　　　　　　　　　　　＋（ｃ＋ｄ＋ｅ）ｘ³＋（ｄ＋ｅ＋１）ｘ²＋（ｅ＋１）ｘ＋１
　　係数比較して、
　　　　　　　　　　　　ａ＝−１、ｂ＝０、ｃ＝１、ｄ＝０、ｅ＝−１

　　よって、求める商は、　ｘ⁶−ｘ⁵＋ｘ³−ｘ＋１


　Ｓ（Ｈ）さんからのコメントです。（平成２７年２月７日付け）

　　 （ｘ²−ｘ＋１）（ｘ²＋ｘ＋１）（ｘ⁴−ｘ²＋１） とQ上可約なので、明らか。

　　ｘ⁸＋ｘ⁴＋１＝（ｘ⁶＋ａｘ⁵＋ｂｘ⁴＋ｃｘ³＋ｄｘ²＋ｅｘ＋ｆ）（ｘ²＋ｘ＋１）＋ｐｘ＋ｑ  が恒等式

　なので、ａ＝-1、ｂ＝0、ｃ＝1、ｄ＝0、ｅ＝-1、ｆ＝1、ｐ＝0、ｑ＝0　を得る。


問題３　心臓形　ｘ＝２ｃｏｓθ−ｃｏｓ２θ、ｙ＝２ｓｉｎθ−ｓｉｎ２θ　（０≦θ≦π）　とｘ軸で囲ま
　　　　れた図形の面積を求めよ。（１級１次レベル）

（解）　ｄｘ/ｄθ＝−２ｓｉｎθ＋２ｓｉｎ２θ、ｄｙ/ｄθ＝２ｃｏｓθ−２ｃｏｓ２θ

　　　ｄｘ/ｄθ＝０　から、　θ＝π/３　で、このとき、　ｘ＝３/２

　　　求める面積をＳとおくと、

　　　Ｓ＝∫_-3^3/2 ｙｄｘ−∫₁^3/2 ｙｄｘ

　　　　＝∫_π^π/3 （２ｓｉｎθ−ｓｉｎ２θ）（−２ｓｉｎθ＋２ｓｉｎ２θ）ｄθ
　　　　　　　　−∫₀^π/3 （２ｓｉｎθ−ｓｉｎ２θ）（−２ｓｉｎθ＋２ｓｉｎ２θ）ｄθ

　　　　＝２∫_π/3^π （２ｓｉｎ²θ＋３ｓｉｎθｓｉｎ２θ＋ｓｉｎ²２θ）ｄθ
　　　　　　　　＋２∫₀^π/3 （２ｓｉｎ²θ＋３ｓｉｎθｓｉｎ２θ＋ｓｉｎ²２θ）ｄθ

　　　　＝２∫₀^π （２ｓｉｎ²θ＋３ｓｉｎθｓｉｎ２θ＋ｓｉｎ²２θ）ｄθ

　　　　＝２∫₀^π （１−ｃｏｓ２θ−（3/2）（ｃｏｓ３θ−ｃｏｓθ）＋（１−ｃｏｓ４θ）/２）ｄθ

　　　　＝２［θ−ｓｉｎ２θ/２−（3/2）（ｓｉｎ３θ/３−ｓｉｎθ）＋（θ−ｓｉｎ４θ/４）/２］₀^π

　　　　＝２（π＋π/２）

　　　　＝３π　　（終）

（コメント）　高校３年生程度の問題でした。

　ここで、　ｘ＝２ｃｏｓθ−２ｃｏｓ²θ＋１＝２（１−ｃｏｓθ）ｃｏｓθ＋１

　　　　　　ｙ＝２ｓｉｎθ−２ｓｉｎθｃｏｓθ＝２（１−ｃｏｓθ）ｓｉｎθ　なので、

　　ｒ²＝（ｘ−１）²＋ｙ²＝４（１−ｃｏｓθ）²　より、極方程式は、　ｒ＝２（１−ｃｏｓθ）

　このとき、求める面積は、

　Ｓ＝(1/2)∫₀^π ｒ²ｄθ＝２∫₀^π（１−２ｃｏｓθ＋ｃｏｓ²θ）ｄθ

　　＝２∫₀^π（１−２ｃｏｓθ＋（１＋ｃｏｓ２θ）/２）ｄθ＝３π　と求められる。

（コメント）　極方程式を用いた方が簡単かも．．．。


問題４　心臓形　ｘ＝２ｃｏｓθ−ｃｏｓ２θ、ｙ＝２ｓｉｎθ−ｓｉｎ２θ　（０≦θ≦π）　をｘ軸のま
　　　　わりに１回転してできる曲面の表面積を求めよ。（１級１次レベル）

（解）　求める面積をＳとおくと、

　（ｄｘ/ｄθ）²＋（ｄｙ/ｄθ）²＝（−２ｓｉｎθ＋２ｓｉｎ２θ）²＋（２ｃｏｓθ−２ｃｏｓ２θ）²

　　　　　　　　　　　　　　　　＝８（１−ｃｏｓθ）＝１６ｓｉｎ²（θ/２）　なので、

　Ｓ＝−２π∫_-3^3/2 ｙ√（１＋ｙ’²）ｄｘ＋２π∫₁^3/2 ｙ√（１＋ｙ’²）ｄｘ

　　＝−２π∫_π^π/3 （２ｓｉｎθ−ｓｉｎ２θ）・４ｓｉｎ（θ/２））ｄθ
　　　　　　　　＋２π∫₀^π/3 （２ｓｉｎθ−ｓｉｎ２θ）・４ｓｉｎ（θ/２）ｄθ

　　＝−８π∫_π^π/3 （２ｓｉｎθｓｉｎ（θ/２）−ｓｉｎ２θｓｉｎ（θ/２））ｄθ
　　　　　　＋８π∫₀^π/3 （２ｓｉｎθｓｉｎ（θ/２）−ｓｉｎ２θｓｉｎ（θ/２））ｄθ

　　＝−８π∫_π^π/3 （ｃｏｓ（θ/２）−ｃｏｓ（３θ/２）＋（１/２）（ｃｏｓ（５θ/２）−ｃｏｓ（３θ/２）））ｄθ
　　　　　　＋８π∫₀^π/3 （ｃｏｓ（θ/２）−（ｃｏｓ（３θ/２）＋（１/２）（ｃｏｓ（５θ/２）−ｃｏｓ（３θ/２）））ｄθ

　　＝−８π∫_π^π/3 （ｃｏｓ（θ/２）＋（１/２）（ｃｏｓ（５θ/２）−３ｃｏｓ（３θ/２）））ｄθ
　　　　　　＋８π∫₀^π/3 （ｃｏｓ（θ/２）＋（１/２）（ｃｏｓ（５θ/２）−３ｃｏｓ（３θ/２）））ｄθ

　　＝−８π［２ｓｉｎ（θ/２）＋（１/５）ｓｉｎ（５θ/２）−ｓｉｎ（３θ/２）］_π^π/3
　　　　　　＋８π［２ｓｉｎ（θ/２）＋（１/５）ｓｉｎ（５θ/２）−ｓｉｎ（３θ/２）］₀^π/3

　　＝−８π（１＋１/１０−１−２−１/５−１）＋８π（１＋１/１０−１）

　　＝−８π・（−３１/１０）＋８π・（１/１０）

　　＝１２８π/５　　（終）

（コメント）　大学１年生程度の問題でした。ただ、計算が大変でしたね！


　よおすけさんが以前準１級を受験し合格されたとのことです。（平成２６年１２月２８日付け）
ということは、問題を作問して投稿し採用されれば、作問料がいただけるということですね！

問題５　次の問いに答えよ。ただし、eは自然対数の底とする。（準１級１次レベル）

（１）　次の不定積分を求めよ。

　　∫1/（x²e^1/x）dx

（２）　次の定積分を求めよ。

　　∫_1/2¹ 1//（x²e^1/x）dx

（解）（１）　１/ｘ＝ｔ　とおくと、　ｄｔ/ｄｘ＝−１/ｘ²　なので、　（１/ｘ²）ｄｘ＝−ｄｔ

　　　　　よって、　与式＝∫ｅ^-ｔ（−ｄｔ）＝ｅ^-ｔ＋Ｃ＝ｅ^-1/x＋Ｃ　ただし、Ｃは積分定数

（２）　（１）より、　与式＝[ｅ^-1/x]_1/2¹＝ｅ^-1−ｅ^-2＝（ｅ−１）/ｅ²　　（終）

（コメント）　高校３年生程度の問題でした。


問題６　ｎを２以上の整数とするとき、分数 （１５ｎ＋２）/（１４ｎ＋３）が可約分数(分母、分子
　　　　が約分できる分数)となるようなｎの一般形を求めよ。また、そのときこの分数を約分
　　　　して既約分数とした分数を求めよ。（１級２次レベル）

（解）　１５ｎ＋２と１４ｎ＋３の最大公約数をｄとおくと、題意より、ｄ＞１　としてよい。

　　　　１５ｎ＋２＝ｐｄ　、１４ｎ＋３＝ｑｄ　　（ｐ、ｑは互いに素な自然数）

　　と書ける。このとき、　（−１４ｐ＋１５ｑ）ｄ＝１７　となり、１７は素数なので、ｄ＝１７

　　　１５ｎ＋２＝１７ｐ　において、　１５・１＋２＝１７　なので、辺々引いて、

　　　１５（ｎ−１）＝１７（ｐ−１）

　　　１５と１７は互いに素なので、　ｎ−１＝１７ｋ　（ｋは自然数）　とおける。

　　　すなわち、　ｎ＝１７ｋ＋１　（ｋは自然数）

　　このとき、　（１５ｎ＋２）/（１４ｎ＋３）＝（１５ｋ＋１）/（１４ｋ＋１）　　（終）

（コメント）　高校１年生程度の問題でした。


問題７　正の整数 ａ、ｂ、ｃ があり、ａ²、ｂ²、ｃ² がこの順に公差ｄ (ｄ＞０)の等差数列をな
　　　　す。このとき、次の問いに答えよ。（１級２次レベル）

(１)　公差ｄは、２４の倍数になることを証明せよ。

(２)　公差が最小値の２４のときの ａ、ｂ、ｃ の値を求めよ。

（解）　題意より、ｂ²−ａ²＝ｃ²−ｂ²＝ｄ　で、ａ²＋ｃ²＝２ｂ²　が成り立つ。

　　平方数は３で割ると余りが ０または１なので、ａ²＋ｃ²＝２ｂ²　が成り立つことから、

　ａ²、ｂ²、ｃ² は、すべて３の倍数か、または、３で割った余りが１の自然数である。

　何れにしても、ｄ＝ｂ²−ａ²＝ｃ²−ｂ²　は、３の倍数となる。

　同様にして、平方数は８で割ると余りが ０または１または４なので、ａ²＋ｃ²＝２ｂ²　が成

り立つことから、ａ²、ｂ²、ｃ² はすべて、８の倍数か、または、８で割った余りが１か、または、

８で割った余りが４の自然数である。

　何れにしても、ｄ＝ｂ²−ａ²＝ｃ²−ｂ²　は、８の倍数となる。

　以上から、３と８は互いに素なので、ｄは、３×８＝２４の倍数になる。

（２）　ｂ²−ａ²＝ｃ²−ｂ²＝２４　より、

　　　（ｂ＋ａ）（ｂ−ａ）＝（ｃ＋ｂ）（ｃ−ｂ）＝２４×１＝１２×２＝８×３＝６×４

　このとき、起こりうる可能性は、

　（イ）　ｂ＋ａ＝２４、ｂ−ａ＝１

　　　これを満たす自然数解は存在しない。

　（ロ）　ｂ＋ａ＝１２、ｂ−ａ＝２

　　　これを解いて、　ｂ＝７、ａ＝５　このとき、ｃ²＝７３　これを満たす自然数解は存在しない。

　（ハ）　ｂ＋ａ＝８、ｂ−ａ＝３

　　　これを満たす自然数解は存在しない。

　（ニ）　ｂ＋ａ＝６、ｂ−ａ＝４

　　　これを解いて、　ｂ＝５、ａ＝１　このとき、ｃ²＝４９　で、ｃ＝７

　以上から、求める値は、　ａ＝１、ｂ＝５、ｃ＝７　　（終）

（コメント）　高校２年生程度の問題でした。当初「２４」をどこから捻出しようかと迷いましたが
　　　　　　２４＝３×８　に気がつけば一気に解決することが出来ました。（２）はおまけの問題
　　　　　　ですね！


問題８　数列{ ａ_n } (ｎ＝１、２、３、…)が、１，２，４，５，７，８，１０，１１，１３，１４，…　で与え
　　　　られている。このとき、次の問いに答えよ。（１級２次レベル）

（１）　第ｎ項 ａ_n をｎの式で表せ。
（２）　級数 Ｓ_ｎ＝Σ_ｋ=1〜ｎ ａ_ｋ²＝１６５１　となるｎの値を求めよ。

（解）（１）　階差数列は、　１，２，１，２，・・・　なので、その第ｎ項は、　｛３＋（−１）^ｎ｝/２

　　　　　よって、ｎ≧２のとき、　ａ_n＝１＋Σ_{ｋ=1〜ｎ-1} ｛３＋（−１）^k｝/２

　　　　　　　　　　　　　　　　　　　　＝１＋（３/２）（ｎ−１）＋｛（−１）^ｎ-1−１｝/４

　　　　　　　　　　　　　　　　　　　　＝（６ｎ−３＋（−１）^ｎ-1）/４

　　　　　　この式は、ｎ＝１のときも成立する。

　　　　　したがって、すべてのｎに対して、　ａ_n＝（６ｎ−３＋（−１）^ｎ-1）/４

（２）　数列{ ａ_n²}：１²，２²，４²，５²，７²，８²，１０²，１１²，１３²，１４²，１６²，１７²，１９²，・・・

　　において、

　１＋４＋１６＋２５＋４９＋６４＋１００＋１２１＋１６９＋１９６＋２５６＋２８９＋３６１＝１６５１

　よって、　ｎ＝１３　である。

（コメント）　高校２年生程度の問題でした。


問題９　ａ≧０、ｂ≧０、ｃ≧０　のとき、不等式　(ａ³＋ｂ³＋ｃ³)⁴≧(ａ⁴＋ｂ⁴＋ｃ⁴)³　が成り
　　　　立つことを示せ。また、等号が成り立つ条件を求めよ。（１級２次レベル）

（解）　ａ、ｂ、ｃ がすべて０のとき、不等式は明らかに成り立つ。

　そこで、ａ、ｂ、ｃ のうち少なくとも一つは０でない場合を考える。不等式の対称性から一般

性を失うことなく、　ａ≠０　で、　ａ≧ｂ≧ｃ　としてよい。

　ｘ＝ｂ/ａ、ｙ＝ｃ/ａ　とおくと、　０≦ｘ≦１　、　０≦ｙ≦１

　このとき、示すべき不等式は、　(１＋ｘ³＋ｙ³)⁴≧(１＋ｘ⁴＋ｙ⁴)³　と書ける。

　０≦ｘ≦１　、　０≦ｙ≦１　より、　ｘ³≧ｘ⁴　、　ｙ³≧ｙ⁴

　よって、　１＋ｘ³＋ｙ³≧１＋ｘ⁴＋ｙ⁴　より、　(１＋ｘ³＋ｙ³)³≧(１＋ｘ⁴＋ｙ⁴)³

　　１＋ｘ³＋ｙ³≧１なので、　(１＋ｘ³＋ｙ³)⁴≧(１＋ｘ³＋ｙ³)³

　以上から、　(１＋ｘ³＋ｙ³)⁴≧(１＋ｘ⁴＋ｙ⁴)³　が成り立つ。

　等号が成り立つのは、　ｘ³＝ｘ⁴　、　ｙ³＝ｙ⁴　、　(１＋ｘ³＋ｙ³)⁴＝(１＋ｘ³＋ｙ³)³

　すなわち、　ｘ³＝ｘ⁴　、　ｙ³＝ｙ⁴　、　ｘ³＋ｙ³＝０　から、　ｘ＝ｙ＝０　のときに限る。

　したがって、ａ≧０、ｂ≧０、ｃ≧０　のとき、不等式　(ａ³＋ｂ³＋ｃ³)⁴≧(ａ⁴＋ｂ⁴＋ｃ⁴)³　が

成り立ち、等号が成り立つのは、ａ、ｂ、ｃ のうち少なくとも２つは０のときに限る。　　（終）

（コメント）　高校２年生程度の問題でした。最初、両辺を展開して、左辺−右辺の計算から
　　　　　　何とかしようとしましたが徒労に終わりました。


問題１０　座標平面上の２点Ａ(ａ，０)、Ｂ(０，ｂ)　(ａ＞０、ｂ＞０)と原点Ｏを頂点とする直角三
　　　　　角形のつくる領域をD とする。Ｄ上で一様分布する２次元の確率変数(X，Y )の相関
　　　　　係ρ(X，Y)を求めたい。これを、次の（１）〜（３）の手続きにしたがって計算せよ。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（１級２次レベル）
（１）　この確率変数の密度関数f (ｘ，ｙ)を求めよ。

（２）　平均E(X)、E(Y)と分散σ_Ｘ²、σ_Ｙ²を求めよ。

（３）　上記の値を使って、相関係数ρ(X，Y)を求めよ。

（解）（１）　△ＡＢＯの面積は、ａｂ/２　なので、(ｘ，ｙ)∈Ｄにおいて、f (ｘ，ｙ)＝ｋ　とおくと、

　　　　ａｂｋ/２＝１　より、ｋ＝２/(ａｂ)　となり、

　　　(ｘ，ｙ)∈Ｄにおいて、f (ｘ，ｙ)＝２/(ａｂ)、Ｄに属さない点(ｘ，ｙ)において、f (ｘ，ｙ)＝０

（２）　E(X)＝∫∫_D ｘf (ｘ，ｙ)ｄｘｄｙ

　　　　　　＝２/(ａｂ)∫₀^ａ ｘ(∫₀^b-bx/aｄｙ)ｄｘ

　　　　　　＝２/(ａｂ)∫₀^ａ (ｂｘ−ｂｘ²/ａ)ｄｘ

　　　　　　＝２/(ａｂ)[ｂｘ²/２−ｂｘ³/(３ａ)]₀^ａ＝２/(ａｂ)・ｂａ²/６＝ａ/３

　E(Ｙ)＝∫∫_D ｙf (ｘ，ｙ)ｄｘｄｙ

　　　　　　＝２/(ａｂ)∫₀^ａ (∫₀^b-bx/aｙｄｙ)ｄｘ

　　　　　　＝２/(ａｂ)∫₀^ａ (ｂ−ｂｘ/ａ)²/２ｄｘ

　　　　　　＝１/(ａｂ)[(−ａ/ｂ)（ｂ−ｂｘ/ａ）³/３]₀^ａ＝１/(ａｂ)・(ａ/ｂ)ｂ³/３＝ｂ/３

　E(X²)＝∫∫_D ｘ²f (ｘ，ｙ)ｄｘｄｙ

　　　　＝２/(ａｂ)∫₀^ａ ｘ²(∫₀^b-bx/aｄｙ)ｄｘ

　　　　＝２/(ａｂ)∫₀^ａ (ｂｘ²−ｂｘ³/ａ)ｄｘ

　　　　　　＝２/(ａｂ)[ｂｘ³/３−ｂｘ⁴/(４ａ)]₀^ａ＝２/(ａｂ)・ｂａ³/１２＝ａ²/６

　同様にして、　E(Ｙ²)＝ｂ²/６

　このとき、　σ_Ｘ²＝E(X²)−E(X)²＝ａ²/６−ａ²/９＝ａ²/１８、σ_Ｙ²＝ｂ²/１８

（３）　定義より、　ρ(X，Y)＝Ｃｏｖ（Ｘ，Ｙ）/(σ_Ｘσ_Ｙ)　である。（Ｃｏｖ（Ｘ，Ｙ）：共分散）

そこで、E(ＸＹ)＝∫∫_D ｘｙf (ｘ，ｙ)ｄｘｄｙ

　　　　＝２/(ａｂ)∫₀^ａ ｘ(∫₀^b-bx/aｙｄｙ)ｄｘ

　　　　＝２/(ａｂ)∫₀^ａ ｘ(ｂ−ｂｘ/ａ)²/２ｄｘ

　　　　＝１/(ａｂ)∫₀^ａ (ｂ²ｘ−２ｂ²ｘ²/ａ＋ｂ²ｘ³/ａ²)ｄｘ

　　　　＝ｂ/ａ[ｘ²/２−２ｘ³/(３ａ)＋ｘ⁴/(４ａ²)]₀^ａ＝ａｂ/１２

　　ここで、　Ｃｏｖ（Ｘ，Ｙ）＝E(（Ｘ−Ｅ（Ｘ）（Ｙ−Ｅ（Ｙ）)＝E（ＸＹ）−Ｅ（Ｘ）Ｅ（Ｙ）

なので、　Ｃｏｖ（Ｘ，Ｙ）＝ａｂ/１２−ａｂ/９＝−ａｂ/３６

　以上から、相関係数は、　ρ(X，Y)＝（−ａｂ/３６）/（ａｂ/１８）＝−１/２　　（終）

（コメント）　大学１年生程度の問題でした。計算がちょっと大変でしたね。


　よおすけさんから問題を頂きました。（平成２６年１２月３０日付け）

　今回は、２級２次レベルの問題で、多項式の積分です。同様の問題がよく出されています。
教科書の例題にもありますので、慣れている方なら問題ないでしょう。
（出典：第121回 2級2次 問題7）

問題１１　座標平面上に、ｙ＝２ｘ²−ｘ＋１　で表される放物線ｇと、ｙ＝ｘ＋５　で表される直
　　　　　線 ｌ がある。このとき、次の問いに答えよ。（２級２次レベル）

（１）　放物線ｇと直線 ｌ との交点の座標を求めよ。

（２）　放物線ｇと直線 ｌ とで囲まれる部分の面積を求めなさい。

（解）（１）　２ｘ²−ｘ＋１＝ｘ＋５　より、　:２ｘ²−２ｘ−４＝０　即ち、ｘ²−ｘ−２＝０

　　　　　　（ｘ−２）（ｘ＋１）＝０　より、　ｘ＝２、−１

　　　　　よって、交点の座標は、　（２，７）、（−１，４）

（２）　求める面積は、　２（２−（−１））³/６＝９　　（終）

（コメント）　高校２年生程度の問題でした。


問題１２　２つの正方行列

、

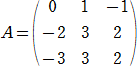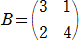　が与えられている。このとき、零行列でない３行２列の行列Ｘで、AX−XB＝O (零行列)　を
　満たすものの一例を求めよ。（１級２次レベル）

（解）　ｄｅｔ（Ａ−λＥ）＝λ³−５λ²−λ＋５＝（λ＋１）（λ−１）（λ−５）＝０　より、

　　　　　Ａの固有値は、１、−１、５

　　ｄｅｔ（Ｂ−λＥ）＝λ²−７λ＋１０＝（λ−２）（λ−５）　より、Ｂの固有値は、２、５

　　Ａの固有値５に属する固有ベクトルは、（Ａ＋Ｅ）（Ａ−Ｅ）の列ベクトルから求められ、

　　^ｔ（０，１，１）である。（→　参考：「固有ベクトルを求める」）

　　また、Ｂの固有値５に属する固有ベクトルは、Ｂ−２Ｅの行ベクトルから求められ、

　　（１，１）である。

　以上から、求める行列の一例として、Ｘ＝^ｔ（０，１，１）（１，１）　をとればよい。すなわち、

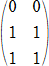　　　　　　　（終）

（コメント）　大学１年生程度の問題でした。６元１次連立方程式を解いてもよかったのですが、
　　　　　　固有値と固有ベクトルを用いる誘惑に負けました！共通の固有値５に着目し、
　　　　　　Ｘ＝^ｔ（０，１，１）（１，１）　とすれば、ＡＸ＝５^ｔ（０，１，１）（１，１）で、また、
　　　　　　ＸＢ＝５^ｔ（０，１，１）（１，１）　から、　ＡＸ−XB＝O (零行列)


問題１３　底面が半径ｒの円で、高さがｈである直円柱Ｒがある。この立体の密度が上面か
　　　　　らの距離に比例しているとき、この円柱の重心の位置を求めよ。（１級２次レベル）

（解）　題意より、求める重心の位置は、密度が端からの距離に比例する長さｈの線分の重

　　心の位置に等しい。比例定数をｋとして、密度は、ｋｘで与えられる。

　　このとき、　∫₀^h ｋｘｄｘ＝ｋｈ²/２　、∫₀^h ｋｘ・ｘｄｘ＝ｋｈ³/３　より、重心の位置は、

　　端より、　（ｋｈ³/３）/（ｋｈ²/２）＝２ｈ/３　の長さの地点にある。　　（終）

（コメント）　大学１年生程度の問題でした。重心の計算は各質点のモーメントの合計が釣り
　　　　　　合う点の計算になりますね！


問題１４　０＜ｘ＜１における微分方程式　ｕ”（ｘ）＝−π²ｓｉｎ（πｘ）　を満たし、２点境界条
　　　　　件 ｕ(０)＝０、ｕ’(１)＝０ を満たす解 u(x) を求めよ。（１級１次レベル）

（解）　ｕ’（ｘ）＝πｃｏｓ（πｘ）＋Ｃ　（Ｃは任意定数）

　　ｕ’(１)＝０ より、−π＋Ｃ＝０　なので、Ｃ＝π　　よって、　ｕ’（ｘ）＝πｃｏｓ（πｘ）＋π

　　さらに、ｕ（ｘ）＝ｓｉｎ（πｘ）＋πｘ＋Ｄ　（Ｄは任意定数）において、ｕ(０)＝０　より、Ｄ＝０

　　よって、　ｕ（ｘ）＝ｓｉｎ（πｘ）＋πｘ　　（終）

（コメント）　大学１年生程度の問題でした。微分方程式という言葉は知らなくても不定積分
　　　　　　の計算で、高校３年生程度かも．．．。


問題１５　次の行列Aの階数を調べよ。ただし、ｘｙｚ≠０　とする。（１級１次レベル）

　　　　

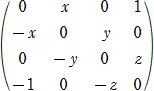
（解）　ｚ＝０　のとき、行列Ａは基本変形により、

　　　　

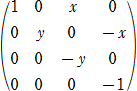
となり、ｙ≠０　のときは、階数４、ｙ＝０　のときは、階数２となる。以下、ｚ≠０　とする。

　行列Ａは基本変形により、

　　　　

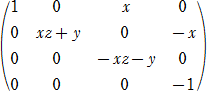
となり、ｘｚ＋ｙ≠０　のとき、階数４、ｘｚ＋ｙ＝０　のときは、階数２となる。

　以上をまとめると、ｘｚ＋ｙ≠０　のとき、階数４、ｘｚ＋ｙ＝０　のときは、階数２となる。　（終）

（コメント）　大学１年生程度の問題でした。私の数学の論文に階数を用いたものがあるので、
　　　　　　懐かしい計算でした！


問題１６　ωをｘ³＝１ の虚数解の１つとするとき、次の行列式Ｄの２乗の値を求めよ。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（１級１次レベル）
　　　　

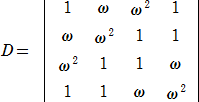
（解）　行列式の計算公式により（→　参考：「行列の必須技法」）

　　Ｄ＝｛（ω²＋１）²−（ω＋１）²｝｛−（ω²−１）²−（ω−１）²｝

　　　＝（ω²＋ω＋２）（ω²−ω）（−ω⁴＋ω²＋２ω−２）

　ω³＝１、ω²＋ω＋１＝０　であるので、Ｄ＝１・（ω²−ω）（−３）＝−３（ω²−ω）

　よって、　Ｄ²＝９（ω²−ω）²＝９（ω⁴−２ω³＋ω²）＝９・（−３）＝−２７　　（終）

（コメント）　大学１年生程度の問題でした。


問題１７　次の連立方程式の実数解の組を求めよ。（１級１次レベル）

　　（３−６ｙ/（ｘ＋ｙ））²＋（３＋６ｙ/（ｘ−ｙ））²＝８２　、ｘｙ＝２

（解）　第一式を変形して、　９（ｘ−ｙ）²/（ｘ＋ｙ）²＋９（ｘ＋ｙ）²/（ｘ−ｙ）²＝８２

　　そこで、　（ｘ−ｙ）²/（ｘ＋ｙ）²＝Ｘ　とおくと、　９Ｘ＋９/Ｘ＝８２　より、

　　　９Ｘ²−８２Ｘ＋９＝０　で、（９Ｘ−１）（Ｘ−９）＝０　より、　Ｘ＝１/９、９

　　Ｘ＝１/９　のとき、　（ｘ−ｙ）/（ｘ＋ｙ）＝１/３、−１/３

　　　（ｘ−ｙ）/（ｘ＋ｙ）＝１/３　のとき、　ｘ−２ｙ＝０　より、　ｘ＝２ｙ

　　ｘｙ＝２　に代入して、２ｙ²＝２　より、　ｙ＝１、−１

　　　よって、（ｘ，ｙ）＝（２，１）、（−２，−１）

　　　（ｘ−ｙ）/（ｘ＋ｙ）＝−１/３　のとき、　２ｘ−ｙ＝０　より、　ｙ＝２ｘ

　　ｘｙ＝２　に代入して、２ｘ²＝２　より、　ｘ＝１、−１

　　　よって、（ｘ，ｙ）＝（１，２）、（−１，−２）

　　Ｘ＝９　のとき、　（ｘ−ｙ）/（ｘ＋ｙ）＝３、−３

　　　（ｘ−ｙ）/（ｘ＋ｙ）＝３　のとき、　ｘ＋２ｙ＝０　より、　ｘ＝−２ｙ

　　ｘｙ＝２　に代入して、２ｙ²＝−２　より、　実数解はない。

　　　（ｘ−ｙ）/（ｘ＋ｙ）＝−３　のとき、　２ｘ＋ｙ＝０　より、　ｙ＝−２ｘ

　　ｘｙ＝２　に代入して、２ｘ²＝−２　より、　実数解はない。

　以上から、　（ｘ，ｙ）＝±（１，２）、±（２，１）　　（終）

（コメント）　高校１年生程度の問題でした。


問題１８　いくつかの続いた正の整数の和が１０００であるとき、この続いた整数の組を求
　　　　　めよ。（準１級２次レベル）

（解）　初項をａ、項数ｎ とすると、末項は、ａ＋ｎ−１なので、そのｎ項の和は、

　　　ｎ（２ａ＋ｎ−１）/２＝１０００　すなわち、　ｎ（ｎ＋２ａ−１）＝２０００＝２⁴・５³

　　　ここで、　ｎ＋２ａ−１＞ｎ　で、ｎ＋２ａ−１とｎは偶奇が反対の正の整数である。

　　　よって、起こりえる可能性は、

　　　（ｎ，ｎ＋２ａ−１）＝（５，４００）、（２５，８０）、（１６，１２５）

　　　（ｎ，ｎ＋２ａ−１）＝（５，４００）　のとき、　ｎ＝５、ａ＝１９８

　　　（ｎ，ｎ＋２ａ−１）＝（２５，８０）　のとき、　ｎ＝２５、ａ＝２８

　　　（ｎ，ｎ＋２ａ−１）＝（１６，１２５）　のとき、　ｎ＝１６、ａ＝５５

　以上から、求める数列は、

　　１９８、１９９、２００、２０１、２０２

　　２８、２９、３０、・・・、５２

　　５５、５６、５７、・・・、７０　　（終）

（コメント）　高校２年生程度の問題でした。


問題１９　ｘ³−ｙ³＝３３１　を満たす正の整数 x 、y を求めよ。（１級１次レベル）

（解）　（ｘ−ｙ）（ｘ²＋ｘｙ＋ｙ²）＝３３１　において、ｘ−ｙ＜ｘ²＋ｘｙ＋ｙ²　で、３３１は素数なので、

　　　ｘ−ｙ＝１　、ｘ²＋ｘｙ＋ｙ²＝３３１

　　ｘ＝ｙ＋１を第２式に代入して整理すると、ｙ²＋ｙ−１１０＝０

　　　（ｙ＋１１）（ｙ−１０）＝０　より、　ｙ＝１０　で、ｘ＝１１　　（終）

（コメント）　高校１年生程度の問題でした。ただし、公式　ｘ³−ｙ³＝（ｘ−ｙ）（ｘ²＋ｘｙ＋ｙ²）
　　　　　　は、現在の学習指導要領では、高校２年で学習することになっている。


問題２０　複素数平面上の点ｚに対して、ｚ，２ｚ，ｚ² が表す点をそれぞれＡ、Ｂ、Ｃとすると
　　　　　き、次の問いに答えよ。（１級１次レベル）

（１）　△ＡＢＣが∠Ｃ＝９０°の直角二等辺三角形であるとき、△ＡＢＣの面積を求めよ。
（２）　ｚ≠０　のとき、AC＝２BC を満たす点Ａの軌跡は円を表す。この円の半径を求めよ。

（解）（１）　題意より、　２ｚ−ｚ²＝±ｉ・（ｚ−ｚ²）　ｚ≠０　としてよいので、

　　　　　　　２−ｚ＝±ｉ・（１−ｚ）　より、　（１±ｉ）ｚ＝２±ｉ　すなわち、　ｚ＝（３±ｉ）/２

　　　　　このとき、　ｚ・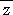＝５/２　なので、△ＡＢＣの面積をＳとおくと、

　　　　　Ｓ＝（１/２）（ｚ−ｚ²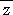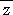）（−²）

　　　　　　＝（１/２）（５/２−（５/２）（ｚ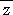＋）＋（５/２）²）

　　　　　　＝（１/２）（５/２−（５/２）・３＋（５/２）²）

　　　　　　＝５/８

（２）　題意より、　｜ｚ²−ｚ｜＝２｜ｚ²−２ｚ｜で、ｚ≠０　より、　｜ｚ−１｜＝２｜ｚ−２｜

　　このとき、点Ａは、点（５/３）と点（３）を結ぶ線分を直径とする円周上にあり、求める半径

　　は、　（１/２）（３−（５/３））＝２/３　となる。　　（終）

（コメント）　高校２年生程度の問題でした。


問題２１　a を定数とする。このとき、実数全体を定義域とする確率密度関数

　　f(ｘ) = a(ｘ−ｘ³)　(0≦ｘ≦1 のとき)　、　f(ｘ) = 0　(ｘ＜０，ｘ＞１ のとき)

について、次の問いに答えよ。（１級１次レベル）

（１）　a の値を求めよ。

（２）　f(ｘ) が定める確率分布の分散を求めよ。（１級１次レベル）

（解）　（１）　∫₀¹a(ｘ−ｘ³)ｄｘ＝ａ（1/2−1/4）＝（1/4）ａ＝１　より、　a = 4

（２）　∫₀¹ｘ・a(ｘ−ｘ³)ｄｘ＝∫₀¹a(ｘ²−ｘ⁴)ｄｘ＝(2/15)ａ＝8/15

　　　∫₀¹ｘ²・a(ｘ−ｘ³)ｄｘ＝∫₀¹a(ｘ³−ｘ⁵)ｄｘ＝(2/15)ａ＝1/3

　　よって、求める分散は、　1/3−（8/15）²＝11/225　　（終）

（コメント）　言葉の定義が把握されていれば容易ですね。


問題２２　（問題文一部改題）

　Ａ、Ｂ、Ｃは、相異なる１〜９のうちの数字で、３桁の数ＡＢＣを平方してある整数を掛けたら
６桁の数ＡＢＣＡＢＣになる。このようなＡＢＣで考えられるものをすべてあげよ。（２級２次）

（コメント）　１４３²×７＝１４３１４３　になるので、解の一つは「１４３」であるが、解がこれだ
　　　　　　けという自信が持てない．．．。


　公益財団法人日本数学検定協会の発表する模範解答に期待していたら、単に「１４３」と
書いてあるだけで素っ気ない。（平成２８年６月３０日付け）

　そこで、解が「１４３」となる道筋を整理したいと思う。

　ｍｏｄ３で、３桁の数ＡＢＣは、Ａ＋Ｂ＋Ｃ　、６桁の数ＡＢＣＡＢＣは、２（Ａ＋Ｂ＋Ｃ）

　かけ算するある整数をＮとおくと、題意より、　Ｎ（Ａ＋Ｂ＋Ｃ）²≡２（Ａ＋Ｂ＋Ｃ）　（ｍｏｄ３）

　すなわち、　（Ａ＋Ｂ＋Ｃ）（Ｎ（Ａ＋Ｂ＋Ｃ）−２）≡０　（ｍｏｄ３）

　これより、　Ａ＋Ｂ＋Ｃ≡０　（ｍｏｄ３）　ならば、　Ｎは任意

Ａ＋Ｂ＋Ｃ≡１　（ｍｏｄ３）　ならば、　Ｎ≡２　（ｍｏｄ３）

Ａ＋Ｂ＋Ｃ≡２　（ｍｏｄ３）　ならば、２Ｎ−２≡０　（ｍｏｄ３）　すなわち、Ｎ≡１　（ｍｏｄ３）

　解の「１４３」、Ｎ＝７は、この場合である。


　DD++さんからのコメントです。（平成２８年６月３０日付け）

　ｘ＝ABC、N＝「ある整数」とすると、Nｘ²＝1001ｘ つまり、Nｘ＝1001

1001＝7×11×13 の約数のうち３桁の数は、11×13＝143　のみ。


（コメント）　なるほど！自然な解法ですね。「合同式」という策に溺れてしまいました。
　　　　　　DD++さんに感謝します。


問題２３　（問題文一部改題）・・・よおすけさんから問題をいただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成３０年８月３１日付け）

図１		図２		図３

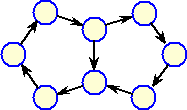
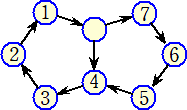
　図１のような、正五角形を２個組み合わせた図形があり、はじめ８個の頂点(○の位置)に、
図２のようにそれぞれ１〜７の番号が書いてあるコマを置き、中央上段の位置は空けておき
ます。

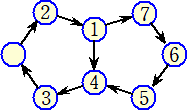
　これらのコマを、図３のように矢印の方向に、空いている位置に移動します。図３は、１と２
のコマを移動したところを表しています。次に３のコマを空いている位置に移動します。

　コマの移動の仕方について、次の２種類を考えます。

　大循環(Tとします)・・・すべてのコマを矢印の方向に１回ずつ空いている位置に移動し、最
　　　　　　　　　　　　　　後に中央上段にあるコマを右上の空いている位置に移動する。

　小循環(Sとします)・・・右側の３つのコマは移動しないで、左側の４つのコマを矢印の方向
　　　　　　　　　　　　　　に１回ずつ空いている位置に移動し、最後に中央上段にあるコマを
　　　　　　　　　　　　　　中央下段に移動する。

　TとSをこの順に施すことを１回の操作と考えます。図２の状態からこの操作を繰り返すと、
操作が終わったときに中央下段にくるコマは、あるいくつかのコマに決まります。

　どのコマになるか、理由を述べて答えなさい。（２級２次レベル）

（解）　コマの移動の仕方から、操作前に「２」の位置にあるコマが中央下段にくるので、求め
　　　るコマは、２と４である。　　（終）


　よおすけさんから問題を頂きました。（平成３０年１０月１５日付け）

　今回は、準１級２次レベルの問題で、問題パターンがほぼ同じなのでまとめてみました。

問題２４

（１）　実数 ｘ、ｙ、ｚ が ｘ＋ｙ＋ｚ＝２ を満たすならば、 ｘｙ＋ｙｚ＋ｚｘ＜２ が成り立つことを示し
　　　なさい。(第220回準1級2次)

（２）　実数 ｘ、ｙ、ｚ が ｘｙ＋ｙｚ＋ｚｘ＝３ を満たすならば、 ｘ＋ｙ＋ｚ≧３ または ｘ＋ｙ＋ｚ≦−３
　　　が成り立つことを示しなさい。(第243回準1級2次)


（解）（１）　（ｘ＋ｙ＋ｚ）²＝ｘ²＋ｙ²＋ｚ²＋２（ｘｙ＋ｙｚ＋ｚｘ）　より、

　　　　　４＝ｘ²＋ｙ²＋ｚ²＋２（ｘｙ＋ｙｚ＋ｚｘ）　なので、　４−２（ｘｙ＋ｙｚ＋ｚｘ）＝ｘ²＋ｙ²＋ｚ²

　　　　　ところで、ｘ＋ｙ＋ｚ＝２ より、実数 ｘ、ｙ、ｚ のうち少なくとも一つは０でないので、

　　　　　　　ｘ²＋ｙ²＋ｚ²＞０　　したがって、　ｘｙ＋ｙｚ＋ｚｘ＜２

（２）　（ｘ＋ｙ＋ｚ）²＝ｘ²＋ｙ²＋ｚ²＋２（ｘｙ＋ｙｚ＋ｚｘ）　より、（ｘ＋ｙ＋ｚ）²＝ｘ²＋ｙ²＋ｚ²＋６

　　ところで、　２（ｘ²＋ｙ²＋ｚ²）≧（ｘ²＋ｙ²）＋（ｙ²＋ｚ²）＋（ｘ²＋ｚ²）≧２（ｘｙ＋ｙｚ＋ｚｘ）＝６

　　より、　ｘ²＋ｙ²＋ｚ²≧３

　よって、　（ｘ＋ｙ＋ｚ）²＝ｘ²＋ｙ²＋ｚ²＋６≧９　より、

　　　ｘ＋ｙ＋ｚ≧３ または ｘ＋ｙ＋ｚ≦−３ が成り立つ。　　（終）


　りらひいさんからのコメントです。（平成３０年１０月１６日付け）

　解いてみましたが、少し時間がかかってしまいました。

（１）　z=2-x-y より、

　　xy+yz+zx=xy+(x+y)(2-x-y)=-x^2-xy-y^2+2x+2y=-(x+y/2-1)^2-3/4*y^2+y+1

　　　　　　　 =-(x+y/2-1)^2-3/4*(y-2/3)^2+4/3≦4/3＜2

（２）　x+y=0 を仮定すると、条件が xy=3 となるが、これらを満たす実数の組は存在しないた
　　め、x+y≠0である。

　　z=(3-xy)/(x+y)=(3-((x+y)^2-(x-y)^2)/4)/(x+y)=-(x+y)/4+(3+(x-y)^2/4)/(x+y)

　より、

　　(x+y+z)^2=(3/4*(x+y)+(3+(x-y)^2/4)/(x+y))^2

　　　　　　　 =(3/4*(x+y)-(3+(x-y)^2/4)/(x+y))^2+3(3+(x-y)^2/4)

　　　　　　　 =(3/4*(x+y)-(3+(x-y)^2/4)/(x+y))^2+3/4*(x-y)^2+9≧9

　よって、x+y+z≧3　または　x+y+z≦-3


　らすかるさんからのコメントです。（平成３０年１０月１６日付け）

　(x+y+z)^2=3(xy+yz+zx)+{(x+y-2z)^2+3(x-y)^2}/4≧3(xy+yz+zx)　から、

　x+y+z=2　のとき、　3(xy+yz+zx)≦(x+y+z)^2=4　すなわち、xy+yz+zx≦4/3＜2

　xy+yz+zx=3　のとき、　(x+y+z)^2≧3(xy+yz+zx)=9　なので、　|x+y+z|≧3


　りらひいさんからのコメントです。（平成３０年１０月１７日付け）

　らすかるさんの

　(x+y+z)^2=3(xy+yz+zx)+{(x+y-2z)^2+3(x-y)^2}/4≧3(xy+yz+zx)

ということは・・・、次の関係式を使うと自由に問題が作れるということですね。高い次数の問
題は解く気がおきないでしょうけど。

　nを2以上の整数、x[1],…,x[n]を実数とすると、次の式が成り立つ。

(Σ[i=1〜n]x[i])^2
＝(n/(n-1))*{ 2*(Σ[i<j]x[i]x[j]) + Σ[k=1〜n-1]((Σ[i=1〜k]x[i])-k*x[k+1])^2/(k(k+1)) }


　ＧＡＩ さんからのコメントです。（平成３０年１０月１７日付け）

　らすかるさんの変形式でもよくこんな式が成立するなと感心していましたが、これがこんな
一般式に広げられるとは驚きです。確かに、

(x1+x2+x3+x4)^2=8/3*(x1*x2+x1*x3+x1*x4+x2*x3+x2*x4+x3*x4)+
　　　　　　　　　　　　　　　　　　　　1/9*{(x1+x2+x3-3*x4)^2+2*(x1+x2-2*x3)^2+6*(x1-x2)^2)}

(x1+x2+x3+x4+x5)^2
=5/2*(x1*x2+x1*x3+x1*x4+x1*x5+x2*x3+x2*x4+x2*x5+x3*x4+x3*x5+x4*x5)+
　1/48*{3*(x1+x2+x3+x4-4*x5)^2+5*(x1+x2+x3-3*x4)^2+10*(x1+x2-2*x3)^2+30*(x1-x2)^2)}

........................................

が成立していくことはビックリです。


　DD++さんからのコメントです。（平成３０年１０月１７日付け）

　意外とみんなやり方が違うものなのですね。私ならこうかな。

(1)　6(xy+yz+zx) = 2(x+y+z)^2 - (x-y)^2 - (y-z)^2 - (z-x)^2 ≦ 8 より

　　xy+yz+zx ≦ 4/3 < 2

(2)　2(x+y+z)^2 = (x-y)^2 + (y-z)^2 + (z-x)^2 + 6(xy+yz+zx) ≧ 18 より

　　(x+y+z)^2 ≧ 9 すなわち x+y+z ≦ -3 または x+y+z ≧3


（コメント）　DD++さんの式変形、美しいですね。参考になります！


　よおすけさんからのコメントです。（平成３０年１０月１７日付け）

　公式の解答は以下の通りでした。

（１）　実数 x、y、z が x+y+z=2 を満たすとき、

　　2(xy+yz+zx)=(x+y+z)^2-(x^2+y^2+z^2)=4-(x^2+y^2+z^2)

　　x+y+z=2　より、(x,y,z)≠(0,0,0)　であるから、　x^2+y^2+z^2＞0

　よって、　2(xy+yz+zx)＜4　すなわち、　xy+yz+zx＜2

※管理人様の解答とほぼ同じ

（２）　xy+yz+zx=3 なので、

　(x+y+z)^2-9=(x+y+z)^2-3×3=(x+y+z)^2-3(xy+yz+zx)

=x^2+y^2+z^2+2(xy+yz+zx)-3(xy+yz+zx)

=x^2+y^2+z^2-(xy+yz+zx)=1/2{(x-y)^2+(y-z)^2+(z-x)^2}

　x、y、z は実数より、　{(x-y)^2+(y-z)^2+(z-x)^2}≧0

　よって、　(x+y+z)^2-9≧0　すなわち、　(x+y+z)^2≧9　がわかり

　x+y+z≧3 または x+y+z≦-3

※DD++さんの解答に、式変形の補足を加えたものと同じ


　りらひいさんからのコメントです。（平成３０年１０月１９日付け）

　対称性を持たせたものですけど、別解を作りました。

　a、b、c を a+b+c=0 かつ (a，b，c)≠(0，0，0) を満たす実数とする。

　(x+y+z)²= 3(xy+yz+zx)+{(ax+by+cz)²+(bx+cy+az)²+(cx+ay+bz)²}/(a²+b²+c²)≦3(xy+yz+zx)

が成り立つので、あとは、x+y+z の値か xy+yz+zx の値を代入すればよい。

　a、b、c に条件を満たす自由な数を入れれば解答が完成します。

　(a，b，c)=(1，-1，0) ならば、DD++さんの解答と一致。

（おまけ）　まったく需要はなさそうですが、なんとなく作ってしまったのでおいておきます。

　mを自然数とする。

(Σ[i=0〜2^m-1]x[i])^2
={ 2^(m+1)*(Σ[0≦i＜j≦2^m-1]x[i]x[j])
　+ Σ[k=1〜m]2^(m-k)*(Σ[i=0〜2^(m-k)-1]((Σ[j=0〜2^(k-1)-1]x[i*2^k+j])
　　　　　　　　　　　　　　　　　　　　　　　　　　-(Σ[j=2^(k-1)〜2^k-1]x[i*2^k+j]))^2) } / (2^m-1)


　よおすけさんから問題を頂きました。（平成３０年１０月２６日付け）

問題２５　∠AOB=90°である直角三角形OABがあります。頂点Oから辺ABに垂線を引き、
　　　　　ABとの交点をHとします。OA=a、OB=b、AH=c、BH=d、OH=h　とするとき、次の問い
　　　　　に答えなさい。

　（１）　ｈ²=cd　が成り立つことを証明しなさい。

　（２）　a²/h²=1+(c/d)　が成り立つことを証明しなさい。（２級２次レベル）

※出典：第125回 数学検定2級2次 問題1

（解）（１）　△ＯＡＨ∽△ＢＯＨ　なので、　ｃ ： ｈ＝ｈ ： ｄ　より、　ｈ²＝ｃｄ　が成り立つ。

（２）　（１）より、　ａ²/ｈ²＝ａ²/ｃｄ

　　△ＯＡＨ∽△ＢＡＯ　なので、　ａ ： ｃ＝ｃ＋ｄ ： ａ　より、　ａ²/ｃ＝ｃ＋ｄ

　　よって、　ａ²/ｈ²＝（ｃ＋ｄ）/ｄ＝１＋ｃ/ｄ


（コメント）　逆ピタゴラスの定理を用いれば、次のような解になります。

　　　　　ａ²/ｈ²＝ａ²（１/ａ²＋１/ｂ²）＝１＋ａ²/ｂ²

　　　　また、　ａ/ｃ＝ｂ/ｈ　、ａ/ｈ＝ｂ/ｄ　より、　ａ²/ｃ＝ｂ²/ｄ　すなわち、　ａ²/ｂ²＝ｃ/ｄ

　　　　よって、　ａ²/ｈ²＝１＋ｃ/ｄ　が成り立つ。


　よおすけさんから問題を頂きました。（平成３０年１１月１２日付け）

問題２６　複素数 z=cos(2π/2018)＋i・sin(2π/2018) について、次の式の値を求めなさい。
　　　　　　ただし、i は虚数単位を表します。

（１）　(1-z)(1-z^2)(1-z^3)・・・(1-z^2016)(1-z^2017)

（２）　1/(1-z)＋1/(1-z^2)＋1/(1-z^3)＋・・＋1/(1-z^2016)＋1/(1-z^2017)

（出典）第327回 実用数学技能検定1級1次 問題2


類題　次の問いに答えよ。

　z=cos(2π/n)＋i・sin(2π/n)、nを2以上の自然数とするとき、

　　　(1-z)(1-z^2)(1-z^3)・・・(1-z^(n-1))

を求めよ。ただし、iは虚数単位とする。（2002年 北海道大学理系 問題4改題）


　問題２６（１）は、類題で、ｎ＝２０１８とすればよいので、類題を示すことにする。これは有名
問題かな？

（解）　z^n=1　より、ｚはｎ次方程式 ｘ^n-1=0 の解である。

　　　よって、　ｘ^n-1=(ｘ-1)(ｘ-z)(ｘ-z^2)(ｘ-z^3)・・・(ｘ-z^(n-1))　と因数分解される。

　　　また、　ｘ^n-1=(ｘ-1)(ｘ^(n-1)+ｘ^(n-2)+・・・+1)　なので、

　　　　(ｘ-z)(ｘ-z^2)(ｘ-z^3)・・・(ｘ-z^(n-1))=(ｘ^(n-1)+ｘ^(n-2)+・・・+1)

　　　ｘ=1 とおくと、　(1-z)(1-z^2)(1-z^3)・・・(1-z^(n-1))=ｎ　　（終）


　さて、（２）を解いてみよう。

（解）　項が全部で２０１７個あり、z^2018＝１ であることに注意して、

　1/(1-z)＋1/(1-z^2017)＝1/(1-z)＋z/(z-1)＝（1-z）/(1-z)＝１

　1/(1-z^2)＋1/(1-z^2016)＝1/(1-z^2)＋z^2/(z^2-1)＝（1-z^2）/(1-z^2)＝１

　　・・・・・・・・・・・・・・・・

　1/(1-z^1008)＋1/(1-z^1010)

＝1/(1-z^1008)＋z^1008/(z^1008-1)＝（1-z^1008）/(1-z^1008)＝１

　また、　z^1009＝cosπ＋i・sinπ＝−１　なので、　　1/(1-z^1009)＝1/2

　よって、求める値は、　１×１００８＋１/２＝２０１７/２　　（終）


　よおすけさんから問題を頂きました。（平成３０年１２月４日付け）

問題２７　F[n]＝２^(2ⁿ)+1　(n＝0,1,2,・・・)　をフェルマー数といいます。

例　F[0]=2^1+1=3　、F[1]=2^2+1=5　、F[2]=2^4+1=17　、F[3]=2^8+1=257　、F[4]=2^16+1=65537
　　はいずれも素数ですが、F[5]=2^32+1=4294967297　は合成数です。
　　(→　4294967297=641×6700417)

　実は、F[n](n≧5)の中に、素数であることが確かめられたものはまだ1つもありません。

　ここでは、比較的簡単な考察によってわかるフェルマー数の性質について考えます。次の
問いに答えなさい。

（１）　m、n を m＜n を満たす 0 以上の整数とします。このとき、F[n]-2 は、F[m]で割り切れ
　　ることを示しなさい。

（２）　次の命題は真ですか偽ですか。真ならばそのことを証明し、偽ならば反例を挙げなさ
　　い。
　　　　　『相異なる２つのフェルマー数の最大公約数はつねに1である。』

（出典：第238回　実用数学技能検定準1級2次 問題5）


（解）（１）　F[n]-2=２^(2ⁿ)-1=２^(2^n-1)・2-1=（２^(2^n-1)-1）（２^(2^n-1)+1）=（２^(2^n-1)-1）F[n-1]

　　　　　　２^(2^n-1)-1=２^(2^n-2)・2-1=（２^(2^n-2)-1）（２^(2^n-2)+1）=（２^(2^n-2)-1）F[n-2]

　　　　よって、　F[n]-2=（２^(2^n-2)-1）F[n-2]F[n-1]　より、帰納的に、

　　　　　　　　　F[n]-2=F[0]F[1]・・・F[n-2]F[n-1]

　　　　が成り立つので、F[n]-2 は、F[m]で割り切れる。（mは m＜n を満たす 0 以上の整数）

（２）　２つのフェルマー数 F[ｍ]、F[ｎ] （m＜n）が１以外の共通因数ｐを持つと仮定すると、

　　　（１）より、　2=F[n]-F[0]F[1]・・・F[n-2]F[n-1]　はｐで割り切れる。すなわち、　ｐ=2

　　　しかるに、フェルマー数 F[n]＝２^(2ⁿ)+1 は奇数なので、これは矛盾する。

　　　よって、相異なる2つのフェルマー数は互いに素となり、命題は真である。　　（終）


　ハンニバル・フォーチュンさんからのコメントです。（平成３０年１２月９日付け）

　『相異なる２つのフェルマー数の最大公約数はつねに1である。』が真ならば、素数は無限
個ある、というわけですね……。


　よおすけさんから問題を頂きました。（平成３０年１２月２３日付け）

問題２８　適当な定数 a、b、c および p、q をとると、５次以下の任意の多項式 f(x) につい
　　　　　て、常に
　　　　　　　　　　　∫_-1¹ f(x)dx＝af(p)＋bf(0)＋cf(q)

　　　　　が成立するようにできます。このような a、b、c、p、q を求めなさい。
　　　　　ただし、p＜0＜q とします。

（出典：第223回実用数学技能検定準1級2次 問題7）


　りらひいさんから解答をいただきました。（平成３０年１２月２４日付け）

　f(x)=1 のとき、　2=a+b+c …(1)

　f(x)=2x のとき、　0=ap+cq …(2)

　f(x)=3x^2 のとき、　2=3ap^2+3cq^2 …(3)

　f(x)=4x^3 のとき、　0=4ap^3+4cq^3 …(4)

　f(x)=5x^4 のとき、　2=5ap^4+5cq^4 …(5)

　f(x)=6x^5 のとき、　0=6ap^5+6cq^5 …(6)

　このとき、　(2)*p^2-(4)/4 より、　0=cp^2q-cq^3　で、p＜0＜q なので、c=0 または p=-q

　c=0 とすると、(2)より、ap=0 となるが、(3)の右辺が 0 となり不適。よって、p=-q

　(2)より、a=c　で、(3)より、2=6cq^2 …(7)　また、(5)より、2=10cq^4 …(8)

　(7)-(8)より、0=6cq^2-10cq^4　で、c≠0、q＞0 なので、q=√(3/5) より、c=5/9

　(1)より、b=8/9

　以上から、　a=5/9　、b=8/9　、c=5/9　、p=-√(3/5)　、q=√(3/5)

　これらは、たしかに(1)〜(6)を満たす。

　また、積分の線型性から5次以下の任意の多項式に関しても成り立つ。


（コメント）　流石！準１級ですね．．．。難問でした。

　りらひいさんの解答を参考に私も考えてみました。

（解）　５次以下の任意の多項式 f(x) を　f(x)＝Aｘ⁵＋Bｘ⁴＋Cｘ³＋Dｘ²＋Eｘ＋F　とおくと、

　∫_-1¹ f(x)dx＝2B/5＋２D/3＋２F

また、af(p)＋bf(0)＋cf(q)

＝（ap⁵＋cq⁵）Ａ＋（ap⁴＋cq⁴）Ｂ＋（ap³＋cq³）Ｃ＋（ap²＋cq²）Ｄ＋（ap＋cq）Ｅ＋（a＋b＋c）Ｆ

で、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ　について恒等的に成り立つので、係数比較して、

　　　　ap⁵＋cq⁵＝０　・・・　（１）

　　　　ap⁴＋cq⁴＝２/５　・・・　（２）

　　　　ap³＋cq³＝０　・・・　（３）

　　　　ap²＋cq²＝２/３　・・・　（４）

　　　　ap＋cq＝０　・・・　（５）

　　　　a＋b＋c＝２　・・・　（６）

　（３）（４）（５）より、　a≠０、ｃ≠０　である。

　（３）（５）より、　ap³＋cq³＝ap³−ap・q²＝ap（p＋q）（p−q）＝０　で、ap（p−q）≠０　から、

　　p＝−q

　（５）より、　（c−a）q＝０　で、q≠０　より、　a＝c

　（２）より、　ap⁴＝１/５　で、（４）より、　ap²＝１/３　なので、p²＝３/５　よって、a＝c＝５/９

　よって、　p＝−√（３/５）　、q＝√（３/５）

　最後に、（６）より、　b＝８/９

　以上から、５次以下の任意の多項式 f(x) について、

　　　　∫_-1¹ f(x)dx＝（５/９）f(−√（３/５）)＋（８/９）f(0)＋（５/９）f(√（３/５）)

が成り立つ。　　（終）


　ハンニバル・フォーチュンさんからのコメントです。（平成３０年１２月２７日付け）

　ガウス・ルジャンドル求積法の特別な場合だったのですね。


　よおすけさんから問題を頂きました。（令和元年７月２６日付け）

問題２９　x=2cos(2π/7)　を零点に持つ有理数係数の多項式P(x)のうち、次数が最小かつ
　　　　　最高次の係数が1であるものを求めなさい。
　　　　（出典：第213回実用数学技能検定1級1次 問題2）


　らすかるさんからのコメントです。（令和元年７月２６日付け）

　y=2cos(4π/7)、z=2cos(8π/7)　とすると、x+y+z=-1、xy+yz+zx=-2、xyz=1　なので、

2cos(2π/7)は、x^3+x^2-2x-1=0　の解。x^3+x^2-2x-1　は既約なので、これが条件を満た

す解。


　ＧＡＩさんからのコメントです。（令和元年７月２６日付け）

　x^3+x^2-2*x-1=0　・・・　ほとんどらすかるさんと同時刻に返事してしまいました。

　では、同じく、　x=2*sin(2π/７）、x=2*tan(2π/7)　を 零点に持つ有理数係数の多項式の
うち、次数が最小かつ最高次の係数が1であるものをそれぞれ求めなさい。


　らすかるさんからのコメントです。（令和元年７月２６日付け）

　{sin(2π/7)}^2+{cos(2π/7)}^2=1 から、x=2sin(2π/7)のとき、√(4-x^2)=2cos(2π/7)　なの

で、2cos(2π/7)　が、x^3+x^2-2x-1=0　の解であることから、2sin(2π/7)　は、

　　(4-x^2)^(3/2)+(4-x^2)-2(4-x^2)^(1/2)-1=0　の解

　整理して、　x^6-7x^4+14x^2-7=0

　これは既約なので、2sin(2π/7)の最小多項式

　{tan(2π/7)}^2+1=1/{cos(2π/7)}^2 から、x=2tan(2π/7)　のとき、

√{16/(x^2+4)}=2cos(2π/7)　なので、2cos(2π/7)　が、x^3+x^2-2x-1=0　の解であることか

ら、2tan(2π/7)　は、{16/(x^2+4)}^(3/2)+{16/(x^2+4)}-2{16/(x^2+4)}^(1/2)-1=0　の解

　整理して、　x^6-84x^4+560x^2-448=0

　これは既約なので、2tan(2π/7)の最小多項式

（補足）　2sin(2π/7)の最小多項式 x^6-7x^4+14x^2-7=0 の6解は、

　±2sin(2π/7)　、±2sin(4π/7)　、±2sin(8π/7)

　2tan(2π/7)　の最小多項式 x^6-84x^4+560x^2-448=0 の6解は、

　±2tan(π/7)　、±2tan(2π/7)　、±2tan(4π/7)

となっていました。

※±2sin(8π/7)=干2sin(π/7)、±2tan(4π/7)=干2tan(3π/7)　ですが、下記の構造を考え
　ると、±2sin(8π/7)、±2tan(4π/7)　と書く方が綺麗です。

　ちなみに、2sin(2π/7)、2sin(4π/7)、2sin(8π/7)　の3解を持つ三次方程式は、

　　x^3-(√7)x^2+(√7)=0

　-2sin(2π/7)、-2sin(4π/7)、-2sin(8π/7)　の3解を持つ三次方程式は、

　　x^3+(√7)x^2-(√7)=0

で、

{x^3-(√7)x^2+(√7)}{x^3+(√7)x^2-(√7)} = (x^3)^2-7(x^2-1)^2 = x^6-7x^4+14x^2-7

　2tan(π/7)、2tan(2π/7)、2tan(4π/7)　の3解を持つ三次方程式は、

　　x^3+(2√7)x^2-28x+(8√7)=0

　-2tan(π/7)、-2tan(2π/7)、-2tan(4π/7)　の3解を持つ三次方程式は、

　　x^3-(2√7)x^2-28x-(8√7)=0

で、

{x^3+(2√7)x^2-28x+(8√7)}{x^3-(2√7)x^2-28x-(8√7)}
= (x^3-28x)^2-7(2x^2+8)^2 = x^6-84x^4+560x^2-448

のようになっていますので、

　2sin(2π/7)/√7　の最小多項式は、x^3-x^2+1/7=0

　tan(2π/7)/√7　の最小多項式は、x^3+x^2-x+1/7=0

ということもわかります。


　よおすけさんからのコメントです。（令和元年７月２７日付け）

（別解の一例）　2π/7=θ　とすると、2π=7θ　で、7θ=4θ+3θと考えると、2π-4θ=3θ

より、cos(2π-4θ)=cos3θ　すなわち、　cos4θ=cos3θ

cos4θ=8(cosθ)^4-8(cosθ)^2+1、cos3θ=4(cosθ)^3-3cosθで、2cosθ=x　だから、

cos4θ=1/2(x^4-4x^2+2)、cos3θ=1/2(x^3-3x)となり、cos4θ=cos3θへそれぞれ置き換え

ると、x^4-4x^2+2=x^3-3x　より、x^4-x^3-4x^2+3x+2=0

　左辺の　x^4-x^3-4x^2+3x+2　をさらに因数分解できるか調べると、(x-2)(x^3+x^2-2x-1)　と
なったため、次数が最小の多項式は、x^4-x^3-4x^2+3x+2ではない。

　これより、x≠2だから、次数が最小のxの多項式は、x^3+x^2-2x-1


問題３０　ｘ^5−ｘ^4−１を因数分解せよ。（１級１次レベル）

　この問題をパっと見てすぐ因数分解できる方は相当の因数分解マニアであろう。

　一番エレガントな解法は、次のようなものだろう。

（解）　ｘ^5−ｘ^4−１＝ｘ^5−ｘ^4＋ｘ^3−ｘ^3−１

　　　　　　　　　　　　＝ｘ^3（ｘ^2−ｘ＋１）−（ｘ−１）（ｘ^2−ｘ＋１）

　　　　　　　　　　　　＝（ｘ^2−ｘ＋１）（ｘ^3−ｘ＋１）　　（終）

　また、「オメガ（ω）の真実」に注意すれば、次のような解法も可能だろう。

（解）　１の３乗根をωとすると、　ω^3＝１、ω^2＋ω＋１＝０　なので、

　ｘ＝−ω　を代入すると、　ｘ^5−ｘ^4−１＝−ω^5−ω^4−１＝−ω^2−ω−１＝０

　ｘ＝−ω~　を代入すると、　ｘ^5−ｘ^4−１＝−ω~^5−ω~^4−１＝−ω~^2−ω~−１＝０

　よって、ｘ^5−ｘ^4−１は、（ｘ＋ω）（ｘ＋ω~）＝ｘ^2−ｘ＋１で割り切れる。

　（ｘ^5−ｘ^4−１）÷（ｘ^2−ｘ＋１）＝ｘ^3−ｘ＋１　なので、

　ｘ^5−ｘ^4−１＝（ｘ^3−ｘ−１）（ｘ^2−ｘ＋１）　　（終）

　また、手数がかかるが次のような解法もありえるだろう。

（解）　ｘ^5−ｘ^4−１＝（ｘ^3＋ａｘ^2＋ｂｘ＋ｃ）（ｘ^2＋ｄｘ＋ｅ）　とおける。

　ｘ^4の係数を比較して、　ｄ＋ａ＝−１

　ｘ^3の係数を比較して、　ｅ＋ａｄ＋ｂ＝０

　ｘ^2の係数を比較して、　ａｅ＋ｂｄ＋ｃ＝０

　ｘの係数を比較して、　ｂｅ＋ｃｄ＝０

　定数項を比較して、　ｃｅ＝−１　なので、　ｃ＝１、ｅ＝−１　または　ｃ＝−１、ｅ＝１

ｃ＝１、ｅ＝−１　とすると、　ｄ＋ａ＝−１　、ａｄ＋ｂ＝１　、−ａ＋ｂｄ＋１＝０　、−ｂ＋ｄ＝０

　　ｂ＝ｄ　なので、　ａ＋ｂ＝−１　、ｂ（ａ＋１）＝１　、ａ−１＝ｂ^2

　　ｂ＝−ａー１　なので、　（ａ＋１）^2＝−１　となり、この式を満たす実数ａは存在しない。

ｃ＝−１、ｅ＝１　とすると、　ｄ＋ａ＝−１　、ａｄ＋ｂ＝−１　、ａ＋ｂｄ−１＝０　、ｂ−ｄ＝０

　　ｂ＝ｄ　なので、　ａ＋ｂ＝−１　、ｂ（ａ＋１）＝−１　、ａ−１＝−ｂ^2

　　ｂ＝−ａー１　なので、　（ａ＋１）^2＝１　となり、　ａ＝０、−２

　　　a＝０　のとき、　ｂ＝−１

　　　ａ＝−２　のとき、　ｂ＝１、ｂ^2＝３　を満たすｂは存在しない。

　以上から、　ｘ^5−ｘ^4−１＝（ｘ^3−ｘ−１）（ｘ^2−ｘ＋１）　　（終）



　　以下、工事中！