逆ピタゴラスの定理なるものがあることを知った。
逆ピタゴラスの定理
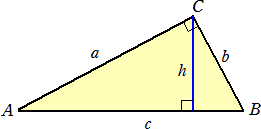
直角を挟む2辺の長さを a、b とし、直角の頂点から斜辺に下ろした垂線の長さを h とす
ると、
1/a2+1/b2=1/h2
が成り立つ。
証明は易しい。
(証) 三平方の定理より、 a2+b2=c2
また、△ABCの面積について、 ch/2=ab/2 より、 c=ab/h
よって、 a2+b2=a2b2/h2
両辺をa2b2で割って、 1/a2+1/b2=1/h2 を得る。 (証終)
例 a=4、b=3 のとき、1/h2=1/a2+1/b2=1/16+1/9=25/(16・9) より、
h=12/5 が直ぐ求められる。
HN「JA1NKA」さんからのコメントです。(平成30年10月26日付け)
「逆ピタゴラスの定理」を興味深く拝見しました。『 1/a2+1/b2=1/h2が成り立つ。』とい
うことは、「ピタゴラスの定理の逆」から、『1/a、1/b、1/h を三辺とする三角形は直角三角形』
ということですよね。
「逆ピタゴラスの定理」は、直角三角形ABCの『双対』な直角三角形に対するピタゴラスの
定理ではなかろうか。
すなわち、辺AB⇔点γ、辺BC⇔点α、辺CA⇔点βと対応させれば、反変ベクトル空間で
の直角三角形ABC、その双対図形は共変ベクトル空間での直角三角形αβγとなる、とい
うことではないでしょうか。
γ=∠Rとし、辺の長さは法線の長さの逆数で、
点A⇔辺βγ(=1/b) 、点B⇔辺γα(=1/a) 、点C⇔辺αβ(=1/h:斜辺となる)
です。物理的には、「実格子ベクトル空間」に対し、「逆格子ベクトル空間」で考える、というこ
とになると思います。
(コメント) 「逆ピタゴラスの定理」にJA1NKAさんと同じような感覚を感じていました。明確な
視座をいただき、ありがとうございます。
S(H)さんから座標幾何の視座をいただきました。(平成30年10月27日付け)
上記の話題は、座標幾何に翻訳すると一般化への道が開かれる。
例1 直線の方程式 x/a+y/b=1 のx切片 a 、y切片 b から、2点A(a,0)、B(0,b)およ
び原点O(0,0)の直角三角形OABにおいて、原点Oと直線との距離hは、
h=1/√(1/a2+1/b2) なので、 1/a2+1/b2=1/h2 が成り立つ。
例2 平面の方程式 x/a+y/b+z/c=1 のx切片 a 、y切片 b 、z切片 c から3点A(a,0,0)、
B(0,b,0)、C(0,0,c)および原点O(0,0,0)の三角錐O-ABCにおいて、原点Oと平
面との距離hは、
h=1/√(1/a2+1/b2+1/c2) なので、 1/a2+1/b2+1/c2=1/h2 が成り立つ。
S(H)さんからの情報によれば、上記の問題は、平成30年度東大大学院新領域創成科学
研究科環境学研究系海洋技術環境学の入試問題らしい。(平成30年10月27日付け)
HN「JA1NKA」さんからのコメントです。(平成30年12月7日付け)
上記の例1で、
h=1/√(1/a2+1/b2) なので、 1/a2+1/b2=1/h2 が成り立つ。
では、証明の方向が逆のような気がします。
命題 直線L:αx+βy+γ=0 と、この直線上にない点C(p,q)との距離hは、
h=|αp+βq+γ|/√(α2+β2)
を使って、hを求めたのだと思われますが、この成立を証明する(求める)には、距離を求め
るので、ピタゴラスの定理を使っているように思われます。
そこで、逆ピタゴラスの定理を使って、命題を証明する方向とします。
つまり、
直角三角形ABCでピタゴラス(三平方)の定理:a2+b2=c2 が成立
⇒(この双対図形を考えれば)逆ピタゴラスの定理:1/a2+1/b2=1/h2 … (1) が成立
⇒ 命題成立。
O-xy座標系で、直線L(線分AB)と点C(p,q)。L:f(x,y)≡αx+βy+γ=0 … (2) と置
く。CはL上にないので、f(p,q)≠0。
原点を C=O’に平行移動し、O’-XY座標系。∠C=∠Rとする直角三角形ABCで、
C:原点O’、CA:X軸、CB:Y軸。X切片:a, Y切片:b として、直線L’(線分AB)は、
X/a+Y/b=1 … (3) と表される。(三角形ができるので、a≠0 かつ b≠0)
(2)に、x=X+p、y=Y+q を代入し、(2) ⇒ L’:αX+βy+f(p,q)=0 … (2)’
I) α≠0 かつ β≠0 の場合
(2)’を(3)の形に式変形し、-X/{f(p,q)/α}−Y/{f(p,q)/β }=1 … (3)’
(3)と(3)’から、 a=−f(p,q)/α、b=−f(p,q)/β … (4)
この|a|、|b|で(1)が成立するから、 1/h2 =(α2+β2)/ {f(p,q)}2
よって、 h=|αp+βq+γ|/√(α2+β2) … (5) が成立
II) αとβの一方が0の場合(両方0はない、意味なし。)
α=0、β≠0 としても一般性を失わない。α⇔β、X⇔Yと入れ替えればよい。
このとき、(2)より、 y=−γ/β、h=| q−y|=|(βq+γ)/β| で、(5)に含まれる。
簡単に、導かれる。
なお、Hesseの標準形も、法線ベクトルを考える。法線ベクトルは直線Lに対しその向きは
一意、位置ベクトルとすれば、その終点が直線Lに対するする双対な点。双対空間(実格子
ベクトル空間に対し逆格子ベクトル空間)で考えることになる。
