
2025(令和7)年8月2日、都内某所で数学教育の講演会があり、拝聴してきた。いくつか
の話題の中で、次の問題に興味を持った。
円周上の5等分点をひとつ置きに結ぶと、次の図形ができる。これは「星型5角形」と言わ
れる。
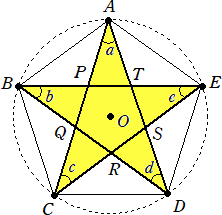
このとき、∠a+∠b+∠c+∠d+∠e=180° が成り立つ。
就職試験にも頻出の問題であるので、読者の方は、どこかで一度はお目にかかっているの
ではと思う。当HPでも、以下のページが参考になるだろう。
・「星形の内角の和」
・「角の大きさ(37)」 ・・・ 星型図形の内角の和
・「凸多角形の考察」
この等式 ∠a+∠b+∠c+∠d+∠e=180° を示すのに、9通りの考え方があると
いうことを、講演された先生は仰っていた。
「えっ、そんなにあるの?」というのが率直な感想であるが、どんな考え方があるのか、整
理してみようと思う。
(考え方 その1) ・・・ もっともよく知られた方法だろう。
∠APT=∠c+∠e 、∠ATP=∠b+∠d なので、△APTにおいて、三角形の内角の
和は180°なので、
∠a+(∠c+∠e)+(∠b+∠d)=∠a+∠b+∠c+∠d+∠e=180°
(考え方 その2)
∠COD=2∠a、∠DOE=2∠b、∠EOA=2∠c、∠AOB=2∠d、∠BOC=2∠e
なので、 2∠a+2∠b+2∠c+2∠d+2∠e=360°
よって、 ∠a+∠b+∠c+∠d+∠e=180°
(考え方 その3)
∠CRD=∠a+∠c+∠d 、∠BRE=180°−(∠b+∠e) において、
対頂角が等しいので、∠CRD=∠BRE より、∠a+∠c+∠d=180°−(∠b+∠e)
よって、 ∠a+∠b+∠c+∠d+∠e=180°
(考え方 その4)
BE‖CD なので、∠BDC=∠b 、∠ECD=∠e 、また、∠CRD=∠a+∠c+∠d
△RCDにおいて、三角形の内角の和は180°なので、
∠b+∠e+(∠a+∠c+∠d)=180°
よって、 ∠a+∠b+∠c+∠d+∠e=180°
(考え方 その5)
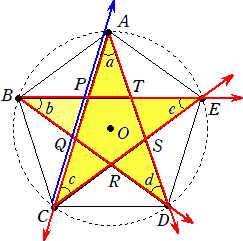
ACを∠a だけ回転させて、ADに移動する。さらに、ADを∠d だけ回転させて、BDに移動
する。さらに、BDを∠b だけ回転させて、BEに移動する。さらに、BEを∠e だけ回転させて、
CEに移動する。さらに、CEを∠c だけ回転させて、CAに移動する。
このとき、ベクトルの向きを考えると、180° 回転していることになるので、
∠a+∠b+∠c+∠d+∠e=180°
(考え方 その6)
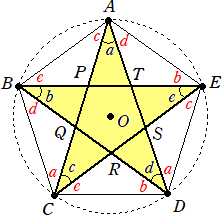
平行線の錯角の性質から、上図のように角度が求まる。
5角形の内角の和は、540° なので、 3(∠a+∠b+∠c+∠d+∠e)=540°
よって、 ∠a+∠b+∠c+∠d+∠e=180°
(考え方 その7)
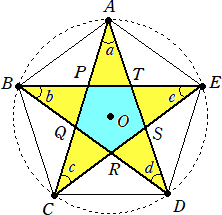
三角形の面積5個分から五角形の外角の和(180°×5−540°=360°)2個分を引
いて、
∠a+∠b+∠c+∠d+∠e=180°×5−360°×2=180°
(追記) kuiperbelt さんより、(考え方 その8)、(考え方 その9)をご投稿いただきました。
(令和7年8月4日付け)
(考え方 その8)
中心Oについて、 ∠COA+∠AOD+∠DOB+∠BOE+∠EOC=144°×5=720°
頂点Aについて、∠OCA+∠OAC+∠COA=180°、∠CAD=∠OAC+∠OAD
頂点B、C、D、Eについても同様で、
∠ODB+∠OBD+∠DOB=180°、∠DBE=∠OBD+∠OBE
∠OEC+∠OCE+∠EOC=180°、∠ECA=∠OCA+∠OCE
∠OAD+∠ODA+∠AOD=180°、∠ADB=∠ODA+∠ODB
∠OBE+∠OEB+∠BOE=180°、∠BEC=∠OEB+∠OEC
両辺を加算すると、
∠CAD+∠DBE+∠ECA+∠ADB+∠BEC+720°=180°×5=900°より、
∠CAD+∠DBE+∠ECA+∠ADB+∠BEC=180°
(考え方 その9)
∠BAEは正5角形の頂点の一つなので、∠BAE=108°
A、B、C、D、Eは、円周の5等分点なので、弧AB=弧BC=弧CD=弧DE=弧EA より、
∠BAC=∠CAD=∠DAE
∠BAC+∠CAD+∠DAE=∠BAE なので、 ∠CAD=108°÷3=36°
∠CAD=∠DBE=∠ECA=∠ADB=∠BEC より、
∠CAD+∠DBE+∠ECA+∠ADB+∠BEC=36°×5=180°
(コメント) kuiperbelt さん、ありがとうございました。
(追記) 令和7年8月5日付け
(考え方 その10) ・・・ 5つの角 ∠a、∠b、∠c、∠d、∠e を一つの頂点に集める。

上図から、 ∠a+∠b+∠c+∠d+∠e=180°
(考え方 その11) ・・・ (考え方 その10)とほぼ同様である。
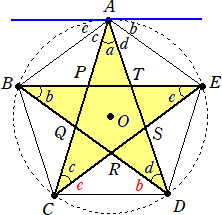
(考え方 その12) ・・・ (考え方 その6)の内部の5角形バージョンである。

∠TPQ=∠a+∠b+∠d、∠PQR=∠b+∠c+∠e、∠QRS=∠a+∠c+∠d、
∠RST=∠b+∠d+∠e、∠STP=∠a+∠c+∠e で、
∠TPQ+∠PQR+∠QRS+∠RST+∠STP=540° より、
3(∠a+∠b+∠c+∠d+∠e)=540°
よって、 ∠a+∠b+∠c+∠d+∠e=180°
(追記) 令和7年8月6日付け
(考え方 その13) ・・・ 外角に注目!
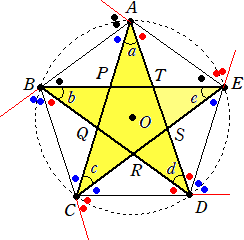
上図において、 ∠a+∠b+∠c+∠d+∠e+(外角の和)=540°
ここで、 (外角の和)=180°×5−540°=360° なので、
∠a+∠b+∠c+∠d+∠e=180°
(コメント) 上記の他にも、もっといろいろな解法があると思います。「これは!」というもの
が見つかったら、是非当HPにご教示下さい。
以下、工事中!