任意の三角形は、その頂点を、円周上に乗せることが可能。
・・・これを、円に埋め込むことが可能ということにする。
四角形の場合は、対角の和がπであれば可能。
五角形の場合は、条件をどのようにすれば可能でしょうか?そのような条件は、不可能で
しょうか?
らすかるさんからのコメントです。(令和4年11月17日付け)
凸五角形ABCDEは、
AC/sin∠B=BD/sin∠C=CE/sin∠D=DA/sin∠E=EB/sin∠A
が成り立っていれば、外接円が存在すると思います。
「角度だけ」や「辺の長さだけ」の条件ではダメです。
また、より一般には、
n角形のn辺それぞれの垂直二等分線(全部でn本)のすべてが1点で交われば外接円が
存在します。
(追記) 上の「角度だけ」は「内角だけ」のつもりでしたが、内角に限らなければ「角度だけ」
でも行けますね。
五角形ABCDEで、 ∠BCE=∠BDE=π-∠A であれば、外接円が存在すると思います。
ks さんからのコメントです。(令和4年11月18日付け)
なるほど、綺麗な条件ですね。これなら一般化もできそうです。直観的には成り立つと思い
ます。
星型図形;凸多角形の対角線を結び閉じた図形
星型図形の内角:隣り合う対角線で囲まれた角
例えば、五芒星の内角の総和は、πである。
証明は、色々あると思います。任意に描いた五芒星は、円に埋め込むことが可能。
そのままでは無理でしょうが、埋め込みが可能の意味を緩くして、角が反時計回りにΘ1、
Θ2,…、Θnとして、同じ順序で埋め込みが可能という意味です。
ks さんからのコメントです。(令和4年11月19日付け)
五芒星の頂点を、A、B、C、D、E とし、その角をΘA、ΘB、ΘC、ΘD、ΘE を円周角と
なるように、それぞれに対応するように中心角をとれば、順番に、同じように角を取ることが
できる。
星型図形の表記として、Nと互いに素な d とおくと、N/d 分数表記できるらしい。
五芒星は、正5/2角形
他の星型 N/d も、緩い意味で埋め込み可能。
ks さんからのコメントです。(令和4年11月22日付け)
星型図形の内角の総和
星型N/d とき、(N/d - 2)dπ とすれば、通常の凸多角形は、d=1とみなせばよい。
(N - 2d)πでもよい。
ks さんからのコメントです。(令和4年11月23日付け)
星型の表記について、「互いに素」にこだわらず、d<n/2 であれば、n/d の表記は有効
であるみたいです。
六点の場合、6/2 とすると、2点ごとに対角線を引くと点が余りますが、同様にして、対角
線を引くと、三角形が2つできます。したがって、内角の総和は、2πです。
総和の公式 (n - 2d)π=(6 - 2・2)π=2π
8/2、9/3、10/2、12/4 なども同様。
ks さんからのコメントです。(令和4年11月28日付け)
凸多角形の対角線を等間隔で描いた図形以外の場合を考えてみました。
例えば、円周上に6点A、B、C、D、E、Fを左周りに適当に配置します。AB=1、BE=3、
EF=1、FC=3、CD=1、DA=3 とします。数字は、長さではなくて、左回りに数えた距離
に無関係な間隔です。
d=(1+3+1+3+1+3)/6=2 (平均値をとる)
公式に代入すると、(6-2・2)π=2π
角度に符号をすると、-の角度がある場合は、角の総和は、不定となり意味を持ちません
ので、+の角のみの時とします。
左回転は+、右回転はーです。色々試して、うまくいきました。
もう一つ、7点を配置して、三角形と四角形を適当に作っても、平均が7で割り切れ、計算
すると、π+2π=3πでうまくいきます。
ks さんからのコメントです。(令和4年12月30日付け)
d の計算 : 左周り(反時計まわり、一定の方向で数える)閉曲線を作る。数えた数の総和
の平均をとる。
例えば、円周上に適当に4点をとる。等間隔でなくてもよい。それを、A、B、C、Dとし、
A、B、D、C、A の順で点を結ぶと、
A~Bは、1 B~Dは、2 D~Cは、3 C~Aは、2
となる。合計1+2+3+2=8 なので、平均は、8÷4=2
したがって、 (4-2×2)π=0 となる。0に意味がある。
例えば、円周上に適当に7点A、B、C、D、E、F、G を配置し、蝶の形と三角形を作ります。
F、G、A、F を順に結んで三角形、F、D、C、E、F を順に結んで蝶の形を作ると、
(1+1+5)+(5+6+2+1)=21で、平均 d=3
よって、 (N - 2d)π=(7-2×3)π=π となり、三角形の内角180°と一致し、蝶の形
の部分が0になるので、都合がよいです。
ks さんからのコメントです。(令和4年12月31日付け)
適用範囲を拡大して、(N-2d)πから(Nー2dーe)πを考える。正の回転だけから、直線、
点を考える。
e;点だけの個数
円周上に、N個の点だけを残した場合、d=0、e=N で、(N-0-N)π=0
4個の配置で、3点で三角形を作り、1点を残すと、1+2+0+1=4 より、d=1、e=1
なので、 (4-2×1-1)π=π 見た目と一致します。
直線の場合、点をAとBとし、AからBをkとすると、BからAは、N-kとなり、和はN、Nで
割って、d=1を得る。二重の線のイメージの閉曲線です。
ks さんからのコメントです。(令和5年1月22日付け)
円周上のN個の点を結ぶ図形の総角の和(まとめ)
0. 等間隔に配置した点を一個づつ結んでできる図形。
正多角形で、内角の総和は、(N - 2)πで与えられる。
1. 配置が等間隔でなくても、点を一個づつ結んでできる図形。
凸多角形で、内角の総和は、(N - 2)πで与えられる。
2.配置が等間隔でなく、点をd個毎に結んでできる図形。
星型図形で、内角の総和は、(N - 2d)π (但し、N≧ 2d、かつ、Nとdは互いに素)
3.配置が等間隔でなく、点をd個毎に結んでできる図形。(互いに素でない場合を含む)
内角の総和は、(N - 2d)π (但し、N≧ 2d dが約数のとき、N/d個の複連結の図形
を作ることができる。余った点からd個づつ繋ぐ。)
中心角と円周角の関係から、導くことができる。
4.連結して結ぶ線の足の長さが同じでなくても公式が適用される。どこを始点に数え始めて
もよいが、必ず反時計回りに数える。隣の点と結ぶ場合、足の長さ c=1 とする。間に1個
おいて結ぶ場合 c=2。以下同様。
c はN-1まで数えることができる。全ての足の長さの和をNで割ったものを d とする。
そうすると、1.2.3.までの結果を含むことになる。但し、N≧2d
この時、角の総和が不定(点の配置によって、総角の和が一定ではない)の図形ができる
ときがある。
不定の図形は、捻じれが生じてるからで、全て正の回転、全て負の回転の場合以外は、不
定になる。
全て負の回転の場合、逆順が全て正の回転になります。
正の回転は、A→B→Cのとき、∠ABCが、Cから見てAが、反時計周りのとき、そうでない
とき、負の回転となる。
不定の図n個のとき、n - 2d の値の総和を e とする。
これは、不定の場合、角の総和を0とみなすため引くことにするためである。
(N=2のとき、直線は不定なので、0となる。N≧3のとき、N - 2d の値としては、1となる。)
N - 2d の値が負になることがあるが、それは逆順であるためで、始点を変えればよい。
絶対値は同じになる。公式 (N - 2d - e)π となる。但し、N≧2d
5.公式を円周上の置換全てに適用することができる。
N個の円周上の点を反時計周りにナンバリング(0 ~ N - 1)する。
0 から N - 1 の全単射で、写像に従って、→で結んだ図形(置換の図)を対象に、公式の
適用を考えることができます。
この時、k から k の写像のときは、足の長さ c=0 とし、単点とよぶことにする。
単点の個数を不定の数 e に加える。
角が不定の場合を除けば、公式 (N - 2d - e)π となる。但し、N≧ 2d
(具体例) N=11個の点を適当に配置しナンバリングする。
全単射(置換) (0,1,2,3,4,5,6,7,8,9,10)→(2,0,5,3,6,8,7,4,9,1,10)
図を描くと、6点の角が不定の図、3点の三角形、単点2個ができる。
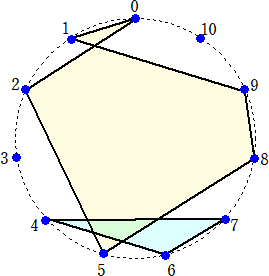
足の長さ c は、点 2 から始めて6個の閉曲線を、点 4 から始めて三角形をつくり、
d = (3+3+1+3+10+2+2+1+8+0+0)/11 = 3
点 3 と 10 は単点で、6点の閉曲線は角が不定でそれ自身の値は、2
よって、e = 2+2 = 4 で、(N - 2d - e)π = (11 - 6 - 4)π = π
したがって、総角は180°で一致します。
ks さんからのコメントです。(令和5年1月25日付け)
安定な図形(点の配置、等間隔に無関係に、円周角の総和が一定である、正の角のみを
もつ図形)のみをもつ図形の種類を数えてみました。
反時計まわりに、ナンバリングしました。
・2点のときは、円周角がないので、0
・3点のときは、三角形がひとつ、逆順も同じ形なので、1種類と考えます。
(0,1,2)⇒(1,2,0)の置換のみ 1個 総和180°
・4点のときは、四角形がひとつ
(0,1,2,3)⇒(1,2,3,0)の置換のみ 1個 総和360°
・5点のときは、五角形と星型のふたつ
(0,1,2,3,4)⇒(1,2,3,4,0)x+1 総和540°
(0,1,2,3,4)⇒(1,2,3,4,0)x+2 総和180°
の二つ。 0,1,1,2と見覚えのある数列
・6点のときは、3種
(012345)⇒(123460)六角形 x+1 総和720°
(012345)⇒(234501)三角形二個x+2 総和360°
他に、三角形が二つの場合も同一視する
(012345)⇒(234051) 総和360°
回転して、重なるものは、同一視する。
ks さんからのコメントです。(令和5年1月27日付け)
N=6 の場合、新たに一個見つかり、フィボナッチ数列の予想が外れましたが、トリボナッチ
の可能性が?
(012345)⇒(143052)
ks さんからのコメントです。(令和5年2月2日付け)
同一視する必要条件は、
1.円周角の総角の和が等しいこと
2.形が同じであること。逆順と回転して同じになる。
逆順は、置換が逆になる。回転は、足跡(足の長さの順番が違うだけ、サイクルは一緒)
例えば、0から始めて、足跡(1122422)の図と、1から始めて(1122422)同じという意味です。
3.二つ以上のサイクルに分かれる時、6点=3+3、7点=3+4、8点=3+5、8点=4+4
サイクルの型が一致。それぞれのサイクルは、同一視できる。
各サイクルのみの部分で考えれば、足跡も一致する。
4.形は異なるが、足跡の数の中身が一致する。(後述)
足跡表示で表せば、始点に無関係に同じ形になる。足跡とは、区間の長さを表示するもの
で、1は隣の点、2は一つ点を越えて線を引くことなど。
7点のときは、7種類
① 足跡表示 (1111111)=7 7角形 x+1 総角 900°
② 足跡表示 (2222222)=14 星型 x+2 総角 540°
③ 足跡表示 (3333333)=21 星型 x+3 総角 180°
④ 足跡表示 (1511114)=14 複体の三角形と四角形 総角 540°
位置や形が違っても、三角形と四角形は全て同一視する。3の内容
⑤ 足跡表示 (1314131)=14 三角形二つと四角形 総角 540°
⑥ 足跡表示 (1122422)=14 総角 540°
⑦ 足跡表示 (1212332)と(1221323)=14 総角 540°
上の二つは見た目は異なるが、足跡の数の内容が一致するので、同一視する。
ks さんからのコメントです。(令和5年2月11日付け)
8点のときは、13種類、全て足跡表示です。
① (11111111)=8 x+1 八角形 総角 1080°
② (22222222)=16 x+2 星型 総角 720°
③ (33333333)=24 x+3 星型 総角 360°
④ (13131313)=16 (4,4)の複体 総角 720°
⑤ (16111114)=16 (3,5)の複体 総角 720°
⑥ (16122525)=24 (3,5)の複体 総角 720°
⑦ (15151515)=24 総角 360°
⑧ (12223222)=16 総角 720°
⑨ (12313213)=16 総角 720°
⑩ (12342121)=16 総角 720°
⑪ (11225221)=16 総角 720°
⑫ (14141131)=16 総角 720°
⑬ (31334343)=24 総角 360°
ks さんからのコメントです。(令和5年2月26日付け)
9点のときは、24種、全て足跡表示です。
① (111111111)
② (2222222222)
③ (333333333)
④ (4444444444)
⑤ (171111114)
⑥ (171226224)
⑦ (1711311616)
⑧ 161111115
⑨ (161122626)
⑩ (123232122)
⑪ (442222443)
⑫ (443122353)
⑬ (442424133)
⑭ (123521211)
⑮ (133131213)
⑯ (334334331)
⑰ (433232334)
⑱ (422211222)
⑲ (341515143)
⑳ (114114114)
(コメント) 当HPの「お茶の時間」-「パズル&クイズ」の「星型の内角の和」で、次の図形
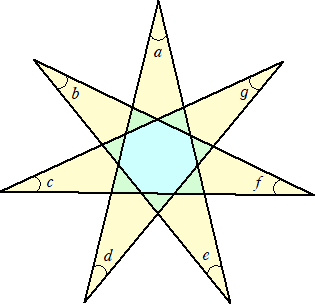
の内角の和 a+b+c+d+e+f+g の値を考察した。そこでは、外角の性質を用いた場
合と、このページで ks さんより提示された公式を用いた場合の解が示されている。
そこで、このような凹角形についての一般的な解法を調べたい。多分、一瞬で分かる方も
いらっしゃるかもしれないが...。。
問題 下図において、角の和 a+b+c+d+e+f+g+h の値を求めよ。
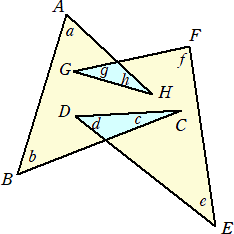
(解) 下図のように補助線を引く。

上図において、 c+d=∠PBE+∠PEB 、g+h=∠QAF+∠QFA なので、
a+b+c+d+e+f+g+h=(四角形ABEFの内角の和)=360° である。 (終)
(別解) ∠CPD=180°-(c+d) より、 図形内の∠BPC=180°+(c+d)
∠GQH=180°-(g+h) より、 図形内の∠AQF=180°+(g+h)
よって、
a+b+180°+c+d+e+f+180°+g+h=(凹六角形の内角の和)=720°
より、 a+b+c+d+e+f+g+h=720°-360°=360° である。 (終)
#捻れた部分を戻して線分に変換されたと思えば、360°というのは一目瞭然ですね!
以下、工事中!
