
下図のような星形の図形がある。
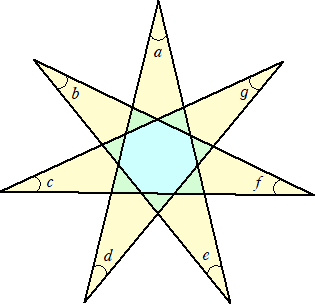
このとき、内角の和 a+b+c+d+e+f+g の値を求めよ。
(答) 180°
実際に、三角形の外角の大きさに着目して、

a+b+c+d+e+f+g=(a+d)+(b+e)+(c+f+g)=180°
(コメント) 円周上のn個の点があり、1つの点から始めてk番目毎に点を結んで星形n角形
を作るとき、内角の和は、一般に、 (n−2k)π で求められる。
特に、k=1のときは、n角形の内角の和 (n−2)π となる。
冒頭の問題については、n=7、k=3を代入して、 (7−2*3)π=π とすればよい。
(→ 参考:「凸多角形の考察」)
以下、工事中!