
下図のように、ABを直径とする半円Oの半円周上に、4点P、Q、R、S をとる。
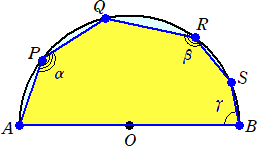
∠APQ=α、∠QRS=β、∠SBA=γ とおくとき、 α+β+γ の値を求めよ。
(答) 360°
DD++ さんからのコメントです。(令和6年6月7日付け)
AB が直径という条件も必要なく、
・円に内接する六角形の内角を 1 つおきに足すと 360°
・円に内接する六角形の外角を 1 つおきに足すと 180°
が成り立つのではないかと思います。
有名な四角形バージョンとあわせて考えると、
・円に内接する 2n 角形の内角を 1 つおきに足すと (n-1)*180°
・円に内接する 2n 角形の外角を 1 つおきに足すと 180°
となりそうですが……簡明な証明はあるでしょうか?
(コメント) 計算のポイントは、円の中心Oと六角形ABCDEの頂点を結んで、2等辺三角形
を5個作るところにあります。このとき、
2(α+β+γ)=180°×5−180° から、 α+β+γ=360° となります。
#ABが直径だと、∠AOB=180°で計算は楽になりますが、ABが直径でない場合は、
同様にして、
2((α+θ)+β+γ)+∠AOB=180°×5 で、 2θ+∠AOB=180° から、
結局、 2(α+β+γ)=180°×5−180° となり、 α+β+γ=360° と同じに
なるんですね!勉強になりました。DD++ さんに感謝します。
GAI さんからのコメントです。(令和6年6月8日付け)
直接関係は無いかもしれませんが、以前から気になっていることがあり、曲率がどこも正
である閉じた曲線C上で(曲率の値は一定でなくても構わない。)、任意の5点をとり、ある点
から1つ飛ばしに直線を引いていくと、中にダビデの星状の図形が構成される。
その星形の内部を塗り潰すと、5個の頂点を持つ図形ができる。
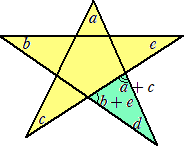
このとき、5つの頂点の内角をすべて足すと、180°となる。
同じく、C上に任意の6点をとり、ある点から1つ飛ばしに直線を引いていくと、閉じた三角
形ができる。続いて、隣の点から1つ飛ばしに直線を引いていくと、閉じた三角形が再びで
きる。
そこで、上の様に中を塗り潰せば今度は、6つの角をもつ星状の図形ができる。
このとき、6つの頂点の内角をすべて足すと、360°となる。
以下同様に、C上に任意の7点をとり、ある点から1つ飛ばしに直線を引いていくと、7個
の頂点を持つ星型図形ができる。
このとき、7つの頂点の内角をすべて足すと、540°となる。
実際に、

において、
から、確かに、7つの頂点の内角をすべて足すと、540°となる。
(追記) 令和6年8月2日付け
(別解)
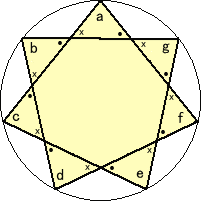
(求める内角の和)+(●の和)+(×の和)=7π において、
(●の和)=2π 、(×の和)=2π
なので、 (求める内角の和)=3π すなわち、 540° となる。 (終)
なお、2つ飛ばしで結んでいくと、その星形図形では、7つの頂点の内角をすべて足すと
180°となる。
実際に、

において、
から、確かに、7つの頂点の内角をすべて足すと、180°となる。
C上に任意の8点をとり、ある点から1つ飛ばしに直線を引いていくとを2度繰り返すと、
8個の頂点を持つ星型図形ができる。
このとき、8つの頂点の内角をすべて足すと、720°となる。
この様に、一般に、1つ飛ばしに結んでいくn角を持つ星状図形で、そのすべての内角の和
をとれば、180*(n−4)°(n≧5) となるは成立すると思われるんですが、どうでしょうか?
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月8日付け)
これ、本当ですか?
六角形の内角をAからFとして、
A = 0.5 * (arc BF) 、E = 0.5 * (arc FD) 、C = 0.5 * (arc DB) 、A + C + E = 0.5*(720°)
から、 A+ C + E = 360°
GAI さんからのコメントです。(令和6年6月8日付け)
B、D、F も結んでください。Aの内角は、∠CAEの部分となります。
三角形ACEから、A+C+E=180°
同じく、三角形BDFから、B+D+F=180°
よって、 A+B+C+D+E+F=360°の意味となります。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月8日付け)
『ある弧に対する中心角は、同一の弧の円周角の2倍である』という定理において、中心
角が180°を超えていても成り立つ、とします。(これ本当ですか?)
まず、六角形 ABCDEF について、これが円に内接することを要請しておきます。この円の
中心をOとします。
∠FAB を、弧BFの円周角とみなします。このとき、弧は長い方、すなわち、C、D、E を通過
するほうの弧とします。
∠FOB を、弧BFの中心角とします。弧の定義は先程と同じです。中心角は 180 °を超え
ることもあります。
同様にして ∠BCD、∠DEF を円周角とみなします。また、∠BOD、∠DOF を中心角とみ
なします。
3つの中心角の総和、∠FOB+∠BOD+∠DOF は、(円を2周しているので)720° となり
ます。
『ある弧に対する中心角は、同一の弧の円周角の2倍である』ので対応する円周角の総
和である∠FAB+∠BCD+∠DEFは、720°の半分、すなわち、360°となります。
《円に内接する六角形の内角を 1 つおきに足すと 360°》と言えることになるのではと。
2n角形についても同様ではないかと?
DD++ さんからのコメントです。(令和6年6月8日付け)
中心角を使えばそうなんですけど、「10 角形のときには 4 周しますよね」といわれても、一
瞬「うーんどうなんですかね」ってなりません?
もっと直感的に、そりゃそうだわってなる証明がないものかなあ、と。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月8日付け)
こっちのほうが直接的ですかね。
2n角形が、円に内接しているので、各頂点と円の中心との間に線分を補助線として引いて
あげると、2n個の二等辺三角形があることになります。二等辺三角形ではふたつの底角が
等しいことに注意し、2n個ある頂角の角度の和は360°であることにも留意します。もちろん
各二等辺三角形の内角の和は180°です。
上からダイレクトに求める公式が得られると思います。
イメージがつきやすいと思うので六角形のケースを。
先の投稿に従い、6つの二等辺三角形を作図します。すなわち、
頂角がA、底角が a の二等辺三角形、頂角がB、底角が b の二等辺三角形、
頂角がC、底角が c の二等辺三角形、頂角がD、底角が d の二等辺三角形、
頂角がE、底角が e の二等辺三角形、頂角がF、底角が f の二等辺三角形
求めたい《ひとつおきの内角の和》は、(f+a)+(b+c)+(d+e) です。
すぐにわかることを並べると、
A+a+a=180°、B+b+b=180°、C+c+c=180°、D+d+d=180°、E+e+e=180°
F+f+f=180°、A+B+C+……=F=360°
上を整理すれば、 (f+a)+(b+c)+(d+e)=360° が得られます。
DD++ さんからのコメントです。(令和6年6月8日付け)
ああ、なるほど、二等辺三角形を作る方法がありましたか。これは確かに簡明。
二等辺三角形を作った後、「だから全内角の総和のピッタリ半分」という方向に行けばもっ
とストレートですかね?
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月12日付け)
GAI さんのコメントについて、以下では、nが奇数のときのみを考えます。(n≧5)
一つおきに点を結ぶ作図により、星型n角形が生まれたものとします。すなわち、この星型
n角形の内部に、凸n角形が作図されたものとします。
(必ず凸になるかどうか…わたしにはわかりませんでした。多分大丈夫?)
このときのみについて以下のように考えます。
・中にある凸n角形の外角の和は、nによらず 360° です。
・凸n角形の各辺に三角形がn個分作図されています。これらの三角形の内角の総和は、
n*180° です。
・求めたい角の総和は後者から前者の2倍を引いたものです。すなわち、 n*180°−720°
よって、GAI さんによる予想: 180*(n−4)° (n≧5) は、上記のように私が設定した強い
条件のもとでは正しそうです。
内部に凸n角形ができない場合は、私にはとてもとても手がつけられませんでした。
n が偶数でも同じ理屈でしょっ、と知人に即座に言われて愕然としました。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月15日付け)
外角を使わない別解を教えてもらいました。
n角形の内角の和をS(n) とします。 S(n) = 180°*(n-2)
(n>=5) のときに求める星型の頂角の角度の和 T(n) は、
T(n) = 2*S(n) -n*S(3) = 180°*(2*n -4) -n*180° = 180°*(n -4)
なるほど……。
(コメント) n=5 の場合について、確認してみました。
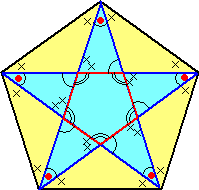
S(5) から、S(3) を5個分差し引くと、「××」が5個分引き残る。そこで、再度、S(5) から、
「×」「×」を5個分差し引くと、「●」が5個分残る。その和が、T(5) となるので、
T(5) = 2*S(5) -5*S(3)
が成り立つ。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年6月24日付け)
GAI さんがおっしゃるに、
C上に任意の7点をとり、ある点から1つ飛ばしに直線を引いていくと、7個の頂点を持つ星
型図形ができる。その星形図形では、7つの頂点の内角をすべて足すと、540°となる。
なお、2つ飛ばしで結んでいくと、その星形図形では、7つの頂点の内角をすべて足すと
180°となる。
一般的に証明するにはどうしたらよいのか、検討がつきません。(→ 参照)
内部に7角形ができていればラッキーなのですけれども、そうとも限りません。

なお、上図はいい加減なので……ご了承ください。一点で3直線が交わると嫌だなあとい
う意味でしかありません。
GAI さんからのコメントです。(令和6年6月25日付け)
曲率がいたるところ正となる閉曲線C上に、nを自然数として、異なる(3*n+4)点を任意にと
り、ある点から隣の2点を飛ばし、次の点を結ぶ線を次々と引いていくと、閉曲線Cの内部に
各点を繋げた星型(3*n+4)角形の図形が現れる。
この時、角星に当たる部分の内角をすべて足し合わせると、180*(3*n-2)°となる。
即ち、星型7角形では180°、星型10角形では720°、星型13角形では1260°、星型16角形
では1800°、・・・・・・・・・・・・・・・ となりそうなんですが・・・
(何回かの作図制作と分度儀による測量結果を基に予測)
この主張は真か偽か?
らすかるさんからのコメントです。(令和6年6月25日付け)
(全頂点の内角の和)+(全頂点の外角の和)=(全頂点の「内角+外角」の和)=(頂点数)×180°
全部の辺をなぞっていくと、3周しますので、 (全頂点の外角の和)=360°×3
よって、 (全頂点の内角の和)=(頂点数)×180°−360°×3=(頂点数−6)×180°
となります。一般には、pn+q点(pとqは互いに素)をとり、p-1点飛ばしでつなげると、内角の
和は、180(p(n-2)+q)°となりますね。
GAI さんからのコメントです。(令和6年6月25日付け)
こんな見事な証明ができるんだ。どれも3周しているなんて思ってもいなかった。例え気付
いていても、何の利用も考え付かなかったと思う。いやーもっと一般に他のパターンでも成り
立つ性質に結びつけられることに感激です。
これを利用させてもらうと、一般に、2*t+3(t=1,2,3,・・・)個の点をC上に配置されたものでは、
ある点から隣の t 個の点を飛ばして次々と繋いでいって行って出来る星型(2*t+3)角形の内
角の和は全て180°を作ることが出来る。
つまり、
星型5角形は、各点を1つ飛ばしで繋ぐ
星型7角形は、各点を2つ飛ばしで繋ぐ
星型9角形は、各点を3つ飛ばしで繋ぐ
星型11角形は、各点を4つ飛ばしで繋ぐ
・・・・・・・・・
星型2*t+3角形は、各点を t 個飛ばしで繋いでいく (t=1,2,3,・・・) ことで、これらの内角の和
は全て180°となってしまうことが起きる!
ks さんからのコメントです。(令和6年7月20日付け)
曲率がいたるところ正となる閉曲線C上に、nを自然数として、異なる(3*n+4)点を任意にと
り、ある点から隣の2点を飛ばし、次の点を結ぶ線を次々と引いていくと、閉曲線Cの内部に
各点を繋げた星型(3*n+4)角形の図形が現れる。
この時、角星に当たる部分の内角をすべて足し合わせると、180*(3*n-2)°となる。
即ち、星型7角形では180°、星型10角形では720°、星型13角形では1260°、星型16角形
では1800°
星形図形の公式 (N−2d)π によれば、N=3n+4、d=3 として出てきます。
(→ 参考:「凸多角形の考察」)
ks さんからのコメントです。(令和6年7月22日付け)
円周上に、N個の点を配置するとき、
星形図形の内角の総和公式: (N−2d)π
の証明です。
1.正N角形の頂点の内角の総和(d=1の場合)
対角線により、N−2個の三角形に分割されますので、内角の総和=(N−2)π
2.N角形の頂点の内角の総和=(N−2)π (d=1の場合)
頂点を等分にしなくても成り立つ。
円周角を一つずつ動かしても、全体の角の総和はかわらない。
3.星形(d個ずつ結んだ場合):N>2d
公約数(N,d)=1 の場合
4.公約数(N,d)=d’>1 の場合
5.円周上にN個の点を取り、12時の点から始め(一般性を失わない)、正の回転(左回りの
意)番号付け(1からN、または、0からN−1)をしておく。すべて頂点A、B、Cの順で結んだ
時、直線ABと直線BCのなす角が正の回転とする。
6.その他、複数の多角形に分割される場合
円周角の性質を利用して証明できます。
ks さんからのコメントです。(令和6年7月23日付け)
(3.の証明) 時計の12時の位置に点を選び、円周をN等分し、その点を選ぶ。12時の点
から始め、一定の間隔dで対角線を結ぶと、N回目に元の12時の位置に戻ることができる。
Nd≡0 (mod N) N'<Nでは、元に戻らない。
一区間の中心角は、2π/Nで、円周角は、π/Nである。一方、その円周角は、区間(N−2d)
の円周角であり、N個ある。
星形図形の内角の総和=(π/N)*(N−2d)*N=(N−2d)π
# N>2d の条件は、同じ形の逆順を避けるためです。
ks さんからのコメントです。(令和6年7月23日付け)
(4.の証明) d=d’ のとき、つまり、dがNの約数、N=de のとき、頂点がe個の多角形が
d個できるので、内角の総和=d*(e−2)π=(de−2d)π=(N−2d)π
ks さんからのコメントです。(令和6年7月25日付け)
(4.の証明) d>d’のとき、N/d’、d/d’ は、ともに整数で、頂点の数N/d’個、足跡の長さ d/d’
の角は、(N/d’−2d/d’)π となり、同じ図形がd’個できるので、出来る図形の内角の総和は、
d’(N/d’−2d/d’)π=(N−2d)π
ks さんからのコメントです。(令和6年7月26日付け)
(5.の証明) 頂点表示:σ1、…、σn (o〜n-1の置換)
足跡表示:d1、…、dn d(i)=σ(i+1)-σ(i)、σ(n+1)=σ(1)
Σd(i)=Σi=1〜N (σ(i+1)-σ(i)) = 0
但し、σ(i)<σ(i+1) のとき、マイナスになるが、左回りで数えるので、d(i) を N-d(i) に置き
換えると、Σd(i)は、Nの倍数となる。つまり、Σd(i)=Nd (dは、平均値)
頂点角表示:e(i)=π/N(N-(d(i)+d(i+1)))
N-(d(i)+d(i+1))>0 (正の角、左回りの角なので)
円周角の総和=Σe(i)
=(π/N)Σ(N-(d(i)+d(i+1)))=(π/N)(N^2-Σ(d(i)+d(i+1)))=(π/N)(N^2-2Nd)=(N-2d)π
ks さんからのコメントです。(令和6年7月27日付け)
(6.の証明) N=n1+…+nk 、nk>3のとき、各nkはサイクルの図形なので、(5.の証明)
と同じ。
説明不足があれば、よろしくお願いします。
以下、工事中!