
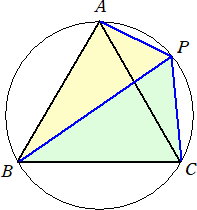
�@���g�o�ł́A�u���T�p�`�̍�}�Ɛ܂莆�v�Ƒ肵�Đ��T�p�`�ɂ����Đ��藧�����ׂ��B
�@�����ł́A�����ȎO�p�`�A�Ⴆ�A���`�b�c�䁢�c�e�b�@�������āA�`�b��
���Ƃ����߂Ă���B�������A���T�p�`�̈�ӂ̒������Q�Ƃ���B
���T�p�`�̐����@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@�@�@
�@���g�o�ł́A�u���T�p�`�̍�}�Ɛ܂莆�v�Ƒ肵�Đ��T�p�`�ɂ����Đ��藧�����ׂ��B
�@�����ł́A�����ȎO�p�`�A�Ⴆ�A���`�b�c�䁢�c�e�b�@�������āA�`�b��![]() �{�P�@�ł���
�{�P�@�ł���
���Ƃ����߂Ă���B�������A���T�p�`�̈�ӂ̒������Q�Ƃ���B
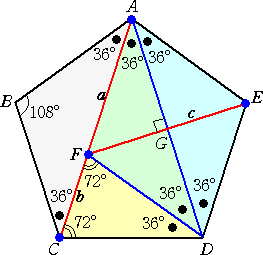 |
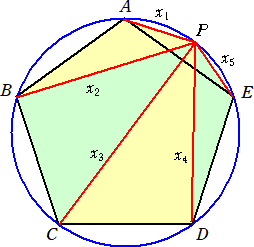
�@ �@�܂��A���}�̂悤�ɁA �@�@�@�@�e�`�����@�A�@�e�b�����@�A�@�e�d���� �@�@�Ƃ����ƁA�u �� �F �� �v��������ł��邱�Ƃ́A�悭 �@�@�m���Ă��邵�A �@�@�@�@�@�@��2�{��2����2 �@�@�����藧�Ƃ����������ʔ����B �@���̂悤�ɁA���T�p�`�ɂ́A���낢��Ȑ������B ��Ă���悤�Ɋ�����B�@�@ |
�@���̃y�[�W�ł́A���T�p�`�̌W��邢�낢��Ȑ����ׂĂ݂����Ǝv���B
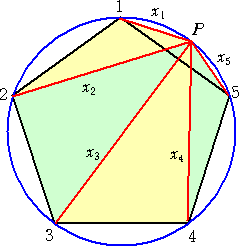 |
�@�@�@�@���}�̂悤�ɁA���T�p�`�̂T���_���A �@�@�@�@�@�@�@�P�@�A�Q�@�A�R�@�A�S�@�A�T �@�@�@�Ƃ��A���T�p�`�̊O�ډ~�̌ʂP�T��̔C�ӂ̓_�o �@�@�@�ɑ��A�e���_�Ɠ_�o�̋������A �@�@�@�@�@��1�@�A��2�@�A��3�@�A��4�@�A��5 �@�@�@�Ƃ����B���̂Ƃ��A �@�@�@�@�@�@��1 �{ ��3 �{ ��5 �� ��2 �{ ��4 �@�@�@�Ƃ������������藧�炵���B |
�@����́A���w�Z�~�i�[�@�f�P�O�@�P�����@�u�G���K���g�ȉ����Ƃށv�Ŗ���Ă������
����B�{���ɐ��藧�̂��ȁH�Ƃ����v������A�܂����ʂȏꍇ���l���Ă݂��B
 |
�@�@�@�@���}�́A�_�o�����_ �P �ɏd�Ȃ��Ă���ꍇ�� �@�@�@����B���T�p�`�̈�ӂ̒������Q�Ƃ���B �@�@�@�@���̂Ƃ��A�@��1 �� �O�@�ŁA �@�@�@�@�@��2 �� ��5 �� �Q�@�A�@��3 �� ��4 �� �@�@�@���A�@�@��1 �{ ��3 �{ ��5 �� �@�@�@�@�@�@�@�@��2 �{ ��4 �� �@�@�@�Ȃ̂ŁA�@��1 �{ ��3 �{ ��5 �� ��2 �{ ��4 |
�@���l�ɁA�_�o�����_ �T �ɏd�Ȃ��Ă���ꍇ���A�@��5 �� �O�@�ŁA
�@��1 �� ��4 �� �Q�@�A�@��2 �� ��3 �� ![]() �{�P
�{�P
���A�@�@��1 �{ ��3 �{ ��5 �� ![]() �{�R�@�A�@��2 �{ ��4 ��
�{�R�@�A�@��2 �{ ��4 �� ![]() �{�R�@�Ȃ̂ŁA
�{�R�@�Ȃ̂ŁA
�@��1 �{ ��3 �{ ��5 �� ��2 �{ ��4�@�����藧�B
�@�u��1�{��3�{��5 �� ��2�{��4�v�Ƃ����������A���T�p�`�̊O�ډ~�̌ʂP�T��̔C�ӂ̓_�o�ɑ�
�Đ��藧�Ƃ͋������I
�@���̖��ɂ��āA��HP�����������b�ɂȂ��Ă���g�m�u�}�l�v���������
���������B�i�����Q�Q�N�P���P�S���t���E�E�E�ꕔ���������C�������Ă��������܂����I�j
 |
�i���j�@�~�̒��S�� �n�A���a�� �P�A�ʂo�P�ɑ��钆�S �@�@�@�p�� �Q�� �Ƃ����B�i �O�����Ɓ��R�U���j �@�@�e���_�Ƃn�A�o�ō��ӎO�p�`���l����ƁA �@�@�@��1���Q�������� �@�@�@��2���Q�������i�Ɓ{�R�U���j �@�@�@��3���Q�������i�Ɓ{�V�Q���j �@�@�@��4���Q�������i�Ɓ{�P�O�W���j���Q�������i�V�Q���|�Ɓj �@�@�@��5���Q�������i�Ɓ{�P�S�S���j���Q�������i�R�U���|�Ɓj �@�ł���B |
| �@���̂Ƃ��A ��1 �{ ��3 �{ ��5 �| ��2 �| ��4 ���Q�������Ɓ{�Q�������i�Ɓ{�V�Q���j�{�Q�������i�R�U���|�Ɓj�|�Q�������i�Ɓ{�R�U���j�|�Q�������i�V�Q���|�Ɓj ���Q�o�������Ɓ{�������i�Ɓ{�V�Q���j�|�������i�V�Q���|�Ɓj�{�������i�R�U���|�Ɓj�|�������i�Ɓ{�R�U���j�p ���Q�i�������Ɓ{�Q�������V�Q���������Ɓ|�Q�������R�U���������Ɓj ���Q�������Ɓi�P�{�Q�������V�Q���|�Q�������R�U���j �@�����ŁA�@�Ӂ��R�U���Ƃ����ƁA�@�T�Ӂ��P�W�O���@����A�@�R�Ӂ��P�W�O���|�Q�� �@����āA�@�������R�Ӂ��������i�P�W�O���|�Q�Ӂj���������Q�Ӂ@���A �@�@�R�������Ӂ|�S������3�Ӂ��Q�������ӂ������� ���̂Ƃ��A�@�R�������Ӂ|�Q�������Ӂi�P�|�������Q�Ӂj���Q�������ӂ������Ӂ@���A �@�@�������Ӂ{�Q�������ӂ������Q�Ӂ��Q�������ӂ������� �@���������āA�@�������Ӂi�P�{�Q�������Q�Ӂ|�Q�������Ӂj���O�@�����藧�B �@���Ȃ킿�A�@�������Ӂ��O�@�Ȃ̂ŁA�@�P�{�Q�������V�Q���|�Q�������R�U�����O�@�����藧�B �@�ȏォ��A�@�@��1 �{ ��3 �{ ��5 �� ��2 �{ ��4�@�����藧�B�@�@�i�I�j�@ |
|
�i�R�����g�j�@�u�}�l�v����̑f���炵���Ɋ������܂����B�}�l����Ɋ��ӂ��܂��B
�@�@�@�@�@�@�����A�����Ə����I�ȏؖ������肻���ȁD�D�D�\���I
�@�O�p����p���āA�ʂȎ��_�ʼn����Ă݂悤�B
�i�ؖ��j�@���}�ɂ����āA�O�ډ~�̒��a���P�Ƃ���B
�@�@
�@�ڂ`�o�a���Ɓ���/�T�@�Ƃ����B���̂Ƃ��A�T�Ɓ��@�ł���B
�@�ڂo�`�d���Ӂ@�Ƃ����ƁA�ڂo�d�`���Ɓ|�Ӂ@�ł���B
�@���o�`�d �ɂ����āA�����藝���A�@�o�`���������i�Ɓ|�Ӂj�@�A�o�d����������
�܂��A�l�p�`�o�b�c�d�ɂ����āA�ڂb�o�d���Q�Ɓ@���A�ڂo�c�b�{�Ӂ��|�Q��
�@����āA�@�ڂo�c�b���|�Q�Ɓ|�Ӂ@�Ȃ̂ŁA���o�b�c �ɂ����āA�����藝���A
�@�o�b���������i�|�Q�Ɓ|�Ӂj���������i�Q�Ɓ{�Ӂj
�@���o�`�a �ɂ����āA�����藝���A�@�o�a���������i�R�Ɓ{�Ӂj���������i�Q�Ɓ|�Ӂj
�@���o�c�d �ɂ����āA�����藝���A�@�o�c���������i�S�Ɓ|�Ӂj���������i�Ɓ{�Ӂj
���̂Ƃ��A
�o�`�{�o�b�{�o�d�|�o�a�|�o�c
���������i�Ɓ|�Ӂj�{�������i�Q�Ɓ{�Ӂj�{�������Ӂ|�������i�Q�Ɓ|�Ӂj�|�������i�Ɓ{�Ӂj
���i�������i�Ɓ|�Ӂj�|�������i�Ɓ{�Ӂj�j�{�i�������i�Q�Ɓ{�Ӂj�|�������i�Q�Ɓ|�Ӂj�j�{��������
���|�Q�������Ƃ������Ӂ{�Q�������Q�Ƃ������Ӂ{��������
���������Ӂi�Q�������Q�Ɓ|�Q�������Ɓ{�P�j
�@�����ŁA�@�Q�������Q�Ɓ|�Q�������Ɓ{�P���S������2�Ɓ|�Q�������Ɓ|�P�@���A
�@�i�������Ɓ{�P�j�i�S������2�Ɓ|�Q�������Ɓ|�P�j
���S������3�Ɓ|�R�������Ɓ{�Q������2�Ɓ|�P���������R�Ɓ{�������Q�Ɓ��Q�������i�T��/�Q�j�������i��/�Q�j
�@�T�Ɓ��@�Ȃ̂ŁA�������i�T��/�Q�j���O�@����A�i�������Ɓ{�P�j�i�S������2�Ɓ|�Q�������Ɓ|�P�j���O
�@�������Ɓ{�P���O�@�Ȃ̂ŁA�@�S������2�Ɓ|�Q�������Ɓ|�P���O
�@����āA�@�o�`�{�o�b�{�o�d�|�o�a�|�o�c���O�@����A�o�`�{�o�b�{�o�d���o�a�{�o�c�@�@�i�I�j
�@�����Q�Q�N�P���P�W���t���ŁA�g�m�u�������v������A�u�g���~�[�̒藝�v��p���ĉ�����|��
���������܂����B
�@�P�ӂ̒������Q�̐��T�p�`�ɂ����āA�Ίp���̒����́A![]() �{�P�@�ł��邱�Ƃɒ��ӂ���B
�{�P�@�ł��邱�Ƃɒ��ӂ���B
�~�ɓ��ڂ���l�p�`�o�P�Q�T�ɂ����āA�@�Q��2���Q��5�{�i![]() �{�P�j��1�@�E�E�E�E�@�i�P�j
�{�P�j��1�@�E�E�E�E�@�i�P�j
�~�ɓ��ڂ���l�p�`�o�P�R�T�ɂ����āA�@�Q��3���i![]() �{�P�j��1�{�i
�{�P�j��1�{�i![]() �{�P�j��5�@�E�E�E�@�i�Q�j
�{�P�j��5�@�E�E�E�@�i�Q�j
�~�ɓ��ڂ���l�p�`�o�P�S�T�@�ɂ����āA�@�Q��4���i![]() �{�P�j��5�{�Q��1�@�E�E�E�@�i�R�j
�{�P�j��5�{�Q��1�@�E�E�E�@�i�R�j
�@����āA�@�i�P�j�|�i�Q�j�@���A�@�Q��2�|�Q��3���i�|![]() �{�P�j��5�@�E�E�E�@�i�S�j
�{�P�j��5�@�E�E�E�@�i�S�j
�@�i�R�j�{�i�S�j�@���A�@�Q��2�|�Q��3�{�Q��4���Q��5�{�{�Q��1
�@���������āA�@��1 �{ ��3 �{ ��5 �� ��2 �{ ��4�@�����藧�B�@
�i�R�����g�j�@�N�₩�ł��ˁI�u�������v����Ɋ��ӂ��܂��B
�@���̖��ɂ��ẮA���ɂ����낢��ȉ����m���Ă���B���w�Z�~�i�[�@�f�P�O�@�S����
�u�G���K���g�ȉ����Ƃށv�̉��Q�l�ɂ��Ă܂Ƃ߂Ă������B
| �i�ʉ����̂P�j | |
 |
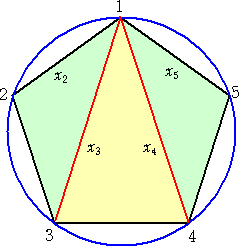
�@�@�@���}�ɂ����āA�~���p �@�@�@�@�ڂP�o�Q�A�ڂQ�o�R�A�ڂR�o�S�A�ڂS�o�T �@�@�͑S�ē������A�@�Q���T���Q����/�T �ł���B �@�@�@����ɁA���}�̂悤�ɐF�������ꂽ�U�̏��}�`�� �@�@�g�ݍ��킹�āA�����}�̂悤�Ȑ}�`�����B �@�@�i�o�P���琔���āA�����Ԗڂ��������Ԃ���Ă��邱 �@�@�Ƃɒ��Ӂj |
 |
�@�@���̂Ƃ��A�~���p �@�@�@�ڂo�`�a�A�ڂ`�a�b�A�ڂa�b�c�A�ڂb�c�d �@�͑S�ē������A�@�Q���T���Q����/�T �ł���B �@�@����ɁA���}�ɂ����āA�@�ڂ`�o�p���Q��/�T�@�Ȃ̂ŁA �@�ڂ`�p�o���|�Q��/�T�|��/�T���Q��/�T�@�ł���B �@�@����āA���`�o�p�͂Q���ӎO�p�`�ƂȂ�B �@���l�ɁA���a�p�q�A���b�q�r�A���c�r�d���Q���ӎO�p�`�B |
�@�ȏォ��A
�@��1 �{ ��3 �{ ��5 �� �i��2 �| �a�p�j �{ �i�a�p �{ �b�r�j �{ �i��4 �| �b�r�j�� ��2 �{ ��4
�����藧�B�@�@�i�I�j
�i�R�����g�j�@�N�₩�ł��ˁI�}�`��g�ݑւ��ĂQ���ӎO�p�`�����o���Ƃ����A�C�f�A�͎v��
�@�@�@�@�@�@���܂���D�D�D�B���l�s�̎R�c��������Ɋ��ӂ��܂��B
�i�NjL�j�@�����Q�Q�N�P�O���P�O���t��
�@���g�o�����������b�ɂȂ��Ă���g�m�u�e�m�v���A��L�̐���
�@�@���T�p�`�`�a�b�c�d���A�~�ɓ��ڂ��Ă���Ƃ���B�ʂ`�d��̔C�ӂ̓_�o�ɑ��āA
�@�o�`�{�o�b�{�o�d���o�a�{�o�c�����藧�B
�̈�ʉ����l����ꂽ�B
�@��L�̐����ɑ������邱�Ƃ��A�� �� �p�`�Ő��藧���ǂ������l���Ă݂悤�B��
��������
����ΐ��藧���Ȃ�����A�� �͊�Ƃ���B
�@�܂��A�����R�@�̏ꍇ���l����B
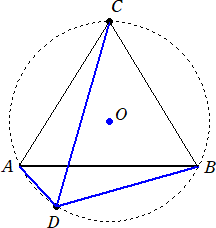
�@���R�p�`�`�a�b���~�ɓ��ڂ��Ă���Ƃ���B
�@�ʂ`�b��̔C�ӂ̓_�o�ɑ��āA�o�`�{�o�b���o�a�@�����藧�B
�@�@
�@����́A�l�p�`�o�`�a�b�Ƀg���~�[�̒藝��K�p����������ɓ�����B
�@���ۂɁA���R�p�`�`�a�b�̈�ӂ� �P �Ƃ���A�o�`�E�P�{�o�b�E�P���o�a�E�P�@�����藧���Ƃ�
�疾�炩���낤�B
�@���T�p�`�̂Ƃ��̏ؖ��͊��ɗ^�����Ă���B�g���~�[�̒藝���g���̂������Ƃ��ȒP�ł�
��B
�@��ӂ̒������Q�Ƃ��āA�Ίp���̒������@![]() �{�P�@�ł��邱�Ƃ��g���Ă��邪�A������g���~
�{�P�@�ł��邱�Ƃ��g���Ă��邪�A������g���~
�[�ŏo�邩��A�g���~�[�̒藝�����ł���Ă݂悤�B
�@�@
�i�ʏj�@��ӂ̒������P�Ƃ��Ίp���̒����� �� �Ƃ��āA���̎l�p�`�Ƀg���~�[�̒藝���g���B
�@�l�p�`�`�a�b�c�ɂ��āA�@�P�E�P�{�P�E�������E���@���A�@�P�{������2�@�E�E�E�i�P�j
�@�l�p�`�o�`�a�b�ɂ��āA�@�o�`�E�P�{�o�b�E�P���o�a�E���@���A�@�o�`�{�o�b�����E�o�a�@�E�E�E�i�Q�j
�@�l�p�`�o�a�b�c�ɂ��āA�@�o�a�E�P�{�o�c�E�P���o�b�E���@���A�@�o�a�{�o�c�����E�o�b�@�E�E�E�i�R�j
�@�l�p�`�o�b�c�d�ɂ��āA�@�o�b�E�P�{�o�d�E�P���o�c�E���@���A�@�o�b�{�o�d�����E�o�c�@�E�E�E�i�S�j
�@�i�Q�j�{�i�S�j���A�@�o�`�{�Q�o�b�{�o�d�����E�i�o�a�{�o�c�j
�@�i�R�j�������āA�@�o�`�{�Q�o�b�{�o�d����2�E�o�b�@���A�@�o�`�{�o�b�{�o�d���i��2�|�P�j�E�o�b
�@�i�P�j���A�@��2�|�P�����@�Ȃ̂ŁA�@�i�R�j���A�@�o�`�{�o�b�{�o�d�����E�o�b���o�a�{�o�c�@������
�@���B�@�@�i�؏I�j
�i�ʏj�@��ӂ̒������P�Ƃ��Ίp���̒����� �� �Ƃ���B
���̂Ƃ��A�@�P �F ���|�P�� �� �F �P�@���A ��2�|�����P�@�Ȃ̂ŁA�@���|�P/�����P�@�����藧�B
�@�l�p�`�`�a�b�o �ɂ����āA�g���~�[�̒藝���A�@�o�`�E�P�{�o�b�E�P�����E�o�a�@�E�E�E�@�@
�@�l�p�`�o�a�b�c�ɂ��āA�@�o�a�E�P�{�o�c�E�P�����E�o�b�@�E�E�E�@�A
�@�l�p�`�o�b�c�d�ɂ��āA�@�o�b�E�P�{�o�d�E�P�����E�o�c�@�E�E�E�@�B
�@�@�{�B�@���A�@�o�`�{�Q�o�b�{�o�d�����E�i�o�a�{�o�c�j�@���Ȃ킿�A
�@�o�`�{�o�b�{�o�d�����E�i�o�a�{�o�c�j�|�o�b
�@�A���A�@�o�b���i�P/���j�i�o�a�{�o�c�j�@�Ȃ̂ŁA�@�o�`�{�o�b�{�o�d���i���|�P/���j�E�i�o�a�{�o�c�j
�����ŁA���|�P/�����P�@�Ȃ̂ŁA�@�o�`�{�o�b�{�o�d���o�a�{�o�c�@�@�i�؏I�j
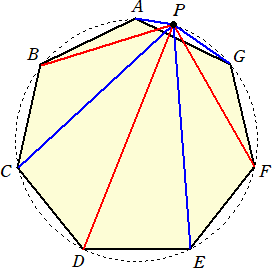
�@���āA�e�m����̏o��ł��B���V�p�`�̏ꍇ�Ɏ��̖�����ؖ����Ă��������B
�@���V�p�`�`�a�b�c�d�e�f���~�ɓ��ڂ��Ă���Ƃ���B�ʂ`�f��̔C�ӂ̓_�o�ɑ��āA
�o�`�{�o�b�{�o�d�{�o�f���o�a�{�o�c�{�o�e�@�����藧�B
�@�@
�@�����Q�Q�N�P�O���P�O���t���ŁA�g�m�u�ۂ��ہv����A
�@���T�p�`�̏ꍇ���g���~�[�̒藝���g�킸�����I�ɏؖ����邱�Ƃ��ł��܂���
�Ƃ̕����B���p����ΐ��V�p�`�ȏ�̏ꍇ�ł��ł������Ƃ������ƂŁA���̏ؖ���
�������B
�i�ʏj�@�܂����̕��������B
�@�~�n�̓����Ɍ��`�a������A�ʂ`�a�̒��_���b�A�b��ʂ�Ȃ����̌ʂ`�a������R�ɓ�
���_���c�Ƃ���Ƃ��A�c�`�{�c�a�Ƃc�b�͔�Ⴗ��B
�@�@
�@���ۂɁA�g���~�[�̒藝�ɂ��A�@�c�b�E�`�a���c�`�E�b�a�{�c�a�E�b�`
�@�����ŁA�@�b�`���b�a�@�ŁA�@�`�a/�b�`�����@�Ƃ����ƁA���͒萔�ŁA�c�`�{�c�a�����E�c�b�@�ƂȂ�B
���Ȃ킿�A�@�c�`�{�c�a �� �c�b �͔�Ⴗ��B
�@���̕��ɂ��A�@�o�`�{�o�b�����E�o�a�@�A�@�o�b�{�o�d�����E�o�c�@�A�@�o�d�{�o�f�����E�o�e
�@�o�`�{�o�f�����E�o�c�@�A�@�o�a�{�o�e�����E�o�c�@�@�i ���A���A�� �͒萔�j
�@�@
�@���������āA�@�Q�o�`�{�Q�o�b�{�Q�o�d�{�Q�o�f�����i�o�a�{�o�c�{�o�e�j�{���E�o�c
�@�܂��A�@�o�a�{�o�e�����E�o�c�@���A�@�Q�o�`�{�Q�o�b�{�Q�o�d�{�Q�o�f���i���{���{�����j�o�c
�@����āA�@�o�`�{�o�b�{�o�d�{�o�f�@�Ɓ@�o�c�@�͔�Ⴗ��B
�@�܂��A�o�c�@�Ɓ@�o�a�{�o�e�@�͔�Ⴗ��̂ŁA�@�o�c�@�Ɓ@�o�a�{�o�c�{�o�e�@�͔�Ⴗ��B
�@����āA�@�o�`�{�o�b�{�o�d�{�o�f�@�Ɓ@�o�a�{�o�c�{�o�e�@����Ⴗ��̂ŁA
�@�@�o�`�{�o�b�{�o�d�{�o�f�����i�o�a�{�o�c�{�o�e�j�@�@�i�� �͒萔�j
�@���ɁA�o���`�@�̂Ƃ��A�@�o�`�{�o�b�{�o�d�{�o�f���o�a�{�o�c�{�o�e�@�Ȃ̂ŁA�@�����P
�]���āA��ɁA�����P�@�ŁA�o�`�{�o�b�{�o�d�{�o�f���o�a�{�o�c�{�o�e�@�����藧�B�@�@�i�؏I�j
�@�ۂ��ۂ���̕ʏɑ��āA�炷���邳��̃R�����g�ł��B�i�����Q�Q�N�P�O���P�P���t���j
�@�ۂ��ۂ���̌v�Z��P�ɒZ�k���������ł����D�D�D���̂悤�ɂ��Ă������ł��ˁB�B
�@�@�o�`�{�o�b�����E�o�a�@�A�@�o�d�{�o�f�����E�o�e�@�A�@�o�a�{�o�e�����E�o�c�@�̂R������
�@�@�o�`�{�o�b�{�o�d�{�o�f�����i�o�a�{�o�e�j�������E�o�c
�@�܂��A�@�o�a�{�o�c�{�o�e���i���{�P�j�o�c
�@����āA�@�o�`�{�o�b�{�o�d�{�o�f�@�Ɓ@�o�a�{�o�c�{�o�e�@�͔�Ⴗ��B
�i�R�����g�j�@�e�m����A�ۂ��ۂ���A�炷���邳��A���肪�Ƃ��������܂��B
�@�ۂ��ۂ���̕����A���T�p�`�̏ꍇ�ɓK�p���Ă݂܂����B
�i�ؖ��j
�@�@
�@���ɂ��A���A�� �͒萔�Ƃ��āA
�@�o�`�{�o�b�����E�o�a�@�A�o�a�{�o�c�����E�o�b�@�A�o�b�{�o�d�����E�o�c�@�A�@�o�`�{�o�d�����E�o�b
���A�@�Q�i�o�`�{�o�b�{�o�d�j�����E�i�o�a�{�o�c�j�{���E�o�b���i��2�{���j�E�o�b
�@����āA�o�a�{�o�c�����E�o�b�@�Ȃ̂ŁA�o�`�{�o�b�{�o�d�����E�i�o�a�{�o�c�j�@�i���͒萔�j�@�Ƃ�����B
�@�����ŁA�o���`�@�̂Ƃ��A�@�`�b�{�`�d�����E�i�`�a�{�`�c�j�@�ŁA�`�b�{�`�d���`�a�{�`�c�@����A
�����P�@�ŁA�@�o�`�{�o�b�{�o�d���o�a�{�o�c�@�����藧�B�@�@�i�؏I�j
�@�炷��������́A���Q���{�P�p�`�ɂ��Ă����l�̖��肪���藧���Ƃ������ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�P�O���P�P���t���j
�i�ؖ��j�@���Q���{�P�p�` �`0�`1�E�E�E�`2n�@�ɂ��āA�ۂ��ۂ���̕����A
�@�@�o�`���{�o�`2��-���������o�`���@�i���� �͒萔�j�@�����藧�B���̂Ƃ��A
�@�o�`1�{�o�`3�{�o�`5�{�E�E�E�{�o�`2��-1���i��1�{��3�{�E�E�E�{����-1�j�o�`��
�@�܂��A�@�o�`0�{�o�`2�{�E�E�E�{�o�`2�����i��0�{��2�{�E�E�E�{����-2�{�P�j�o�`��
�@����āA
�@�o�`1�{�o�`3�{�o�`5�{�E�E�E�{�o�`2��-1�@�́A�@�o�`0�{�o�`2�{�E�E�E�{�o�`2���@�ɔ�Ⴗ��B
�@�o���`0�@�Ƃ����āA���萔�́A�P �ƂȂ�B���������āA
�@�@�o�`1�{�o�`3�{�o�`5�{�E�E�E�{�o�`2��-1���o�`0�{�o�`2�{�E�E�E�{�o�`2���@�i�؏I�j
�@���āA�e�m����́A���̖���̋t�����藧���ǂ����ɊS�������ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�P�O���P�P���t���j
�@�t�͐��藧�����낤���B�����A���̖��肪���藧���낤���B
�@�T�p�`�`�a�b�c�d���~�ɓ��ڂ��Ă���B�ʂ`�d��̔C�ӂ̓_�o�ɑ��āA
�@�@�@�@�o�`�{�o�b�{�o�d���o�a�{�o�c
�@�����藧�ĂA�T�p�`�`�a�b�c�d�́A���T�p�`�ł���B
�@�_�o���R�p�`�̒��_�ƈ�v�����邱�Ƃɂ��A���R�p�`�ł��邱�Ƃ��������̂ŁA�R�p�`
�̏ꍇ�͐��藧�B
�@�܂��A�R�p�`�̏ꍇ�͂����Ƌ������̖��肪���藧���낤���B
�@�R�p�`�`�a�b���~�ɓ��ڂ��Ă���B�ʂ`�b��̈قȂ�Q�_�o�ɑ���
�@�@�o�`�{�o�b���o�a
�@�����藧�Ă�ABC�͐��R�p�`�ł���B
�@���̂e�m����̖��ɂ��āA�炷���邳�㐔�I�ɉ����ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�P�O���P�P���t���j
�i���j�@�~��P�ʉ~�Ƃ��A�`( �������� �C�������� )�A�b( �������� �C�|��������
)�A�a( �������� �C�������� )�@�Ƃ���B
�@�������A�@�|�����������������@�ł���B���̂Ƃ��A�o( �������� �C�������� )�@�Ƃ��āA
�o�`�{�o�b���o�a�@���`��ɒ��ӂ��Ȃ���a�ς̌����Ȃǂ��g���Đ�������ƁA
�@�Q�������o�i���|���j/�Q�p�{�Q�������o�i���{���j/�Q�p���Q�������o�i���|���j/�Q�p�@���
�@�@�������o�i���|���j/�Q�p�{�������o�i���{���j/�Q�p���������o�i���|���j/�Q�p
�@�Q�������i��/�Q�j�������i��/�Q�j���������i��/�Q�j�������i��/�Q�j�|�������i��/�Q�j�������i��/�Q�j
�@�Q�������i��/�Q�j���������i��/�Q�j�|�������i��/�Q�j�������i��/�Q�j
����āA�@�������i��/�Q�j�������i��/�Q�j���������i��/�Q�j�|�Q�������i��/�Q�j
�@�����ŁA�@�����@�Ƃ���ƁA�@�O���P�|�Q�������i��/�Q�j�@���A�@�������i��/�Q�j���P/�Q
����āA�@��/�Q����/�U�@���A�@������/�R
�@����͐��O�p�`�̏ꍇ�ŁA�C�ӂ� �� �ɑ��āA�o�`�{�o�b���o�a�@�����藧�B
�@�i�����A������/�R�@�Ȃ�A�o�`�{�o�b���o�a�@�ƂȂ�o�͑��݂��Ȃ��B�j
�@�����̂Ƃ��A�@�������i��/�Q�j���o�������i��/�Q�j�|�Q�������i��/�Q�j�p/�������i��/�Q�j
�@�E�ӂ͒萔�ŁA�|��/�Q����/�Q����/�Q�@������A�� �͗B��Ɍ��܂�B
�@|��|���� �Ȃ�Ή��͈�A|��|���� �Ȃ�Ή��Ȃ��Ȃ̂ŁA�o�`�{�o�b���o�a �ƂȂ�o�͍��X1�B
����āA�����Q�ȏ゠��̂͐��O�p�`�̏ꍇ�̂݁B�@�i�I�j
�@�炷���邳��̏ؖ��ɑ��āA�e�m����̃R�����g�ł��B�i�����Q�Q�N�P�O���P�Q���t���j
�@���ꂢ�ȏؖ��ł��ˁB��ԍŏ��� �o�`���Q�������i�i���|���j/�Q�j�j �͐}�������Όv�Z�Ȃ��ŏo
�܂��ˁB�����̖���ł����珉���I�ȏؖ��ɂ�����肽���Ȃ�̂ł����A�ȒP��
�͂ł��Ȃ��̂ł��傤�B���̌`�Ŗ��Ƃ��Ďc���Ă����܂��B
�@�T�p�`�`�a�b�o�p�~�ɓ��ڂ��Ă��āA�o�`�{�o�b���o�a�A�p�`�{�p�b���p�a
�����藧���Ă���B
���̂Ƃ��A��ABC�����O�p�`�ł��邱�Ƃ������I�ɏؖ�����B
�@�e�m���A�u�T�p�`�ł͋t�͐������Ȃ��v���Ƃ������ꂽ�B�i�����Q�Q�N�P�O���P�P���t���j
�i�ؖ��j�@�b��ʂ钼�a�Ɋւ���A��E�AB��D���Ώ̂ɂȂ�悤�Ɏ��B
�@�炷���邳��̏ؖ��Ɠ��l�ɂ��āA�o�`�{�o�d�����o�b�@�A�@�o�a�{�o�c�����o�b
�]���āA�@�o�`�{�o�b�{�o�d���i���{�P�j�o�b�@�A�o�a�{�o�c�����o�b�@�ƂȂ�A�o�`�{�o�b�{�o�d�@��
�o�a�{�o�c�@�͔�Ⴗ��B������A�o���`�@�̂Ƃ��ɓ������Ȃ�A��ɐ��藧�B
�@�����ŁA�@�`�b�{�`�d���`�a�{�`�c�@�ƂȂ�悤�ɁA�`�A�a�A�c�A�d ������悢�B
�@�b�Ƃ`�A�d���Œ肵�A�a���`����b�܂œ������B(�������c���Ώ̂ɂȂ�悤�ɓ�����)
�@���ӂ� �`�b�{�`�d�@�͈��ł���A�E�ӂ̂`�a�{�`�c�@�͂a���`�̂Ƃ��A�`�d�A�a���b�̂Ƃ��A
�Q�`�b�@�i�`�d���`�b�j�@�ɂƂ��Ă����A�`�d���`�b�{�`�d���Q�`�b�@�ł��邩��A
�@����a�A�c�ɂ��āA�`�b�{�`�d���`�a�{�`�c�ɂł���B
�@�ȏォ��A���T�p�`�ȊO�ɏ����������̂͂�������B�@�i�؏I�j
�@�炷���邳�A�o�`�{�o�b�{�o�d���o�a�{�o�c�@�����T�p�`����̓I�ɍ\�����ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�P�O���P�P���t���j
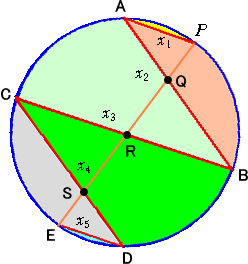
�@�܊p�`�`�a�b�c�d�ɂ����āA
�@�`(41/50�C3��91/50)�@�A�a(-7/25�C24/25)�@�A�b(-1�0)�@�A�c(-7/25�C-24/25)�@�A
�@�d(41/50�C-3��91/50)
�Ƃ���悢�B
�i�NjL�j�@�����Q�V�N�X���R���t��
�@���̒����̘a�Ɋւ���l�@�Ƒ肵�āA�}�g��w�t����ꍂ�Z�Q�N�̗с@�r��A�}�X�E
�t�F�X�^�i�����Q�T�N�W���A�G�����������j�Ō������\���ꂽ�B
�@�~�ɓ��ڂ��Ă��鐳�Q���{�P�p�`A1A2A3�E�E�EA2nA2n+1������A��A1A2n+1��ɓ_�o���Ƃ�B
����PA���̒����������Ƃ���Ƃ��A���̓���
�@��1�{��3�{��5�{�c�{��2n-1�{��2n+1����2�{��4�{��6�{�c�{��2n-2�{��2n
���������邱�Ƃ������B�����P �����A���O�p�`�̏ꍇ�ɏ㎮�����藧���Ƃ͂悭�m��ꂽ
�����ł���B�g���~�[�̒藝���疾�炩�ł���B
���@��L�Ŋ��ɁA�炷���邳��ɂ���ؖ����^�����Ă��邪�A�т���̏ؖ��͕ʏƂȂ�
�@�@���낤�B
�i�ؖ��j�@�_�o�Ɛ��Q���{�P�p�`�̘A�������R���_����Ȃ�l�p�`���l����B���̂悤�Ȏl�p�`
�@�́A�S���� �Q���{�P����BA1A2�����AA1A3���� �Ƃ��āA���ꂼ��ɂ��āA�g���~�[�̒�
�����A�@���i��1�{��3�j������2�@�A���i��2�{��4�j������3�@�A�E�E�E�E�E
�@�����̓��������āA
�@���i��1�{��3�j������2�@�A���i��3�{��5�j������4�@�A�@�E�E�E�E�E�E�@�A���i��2n-1�{��1�j������2n
�@����3�����i��2�{��4�j�@�A����5�����i��4�{��6�j�@�A�@�E�E�E�E�E�E�@�A����2n-1�����i��2n-2�{��2n�j
�@����ɁA����2n+1�{����1������2n�@�A����1�{����2n+1������2
�@������ӁX�����āA
�@�i�Q���{���j�i��1�{��3�{��5�{�c�{��2n-1�{��2n+1�j���i�Q���{���j�i��2�{��4�{��6�{�c�{��2n-2�{��2n�j
�@����āA�@��1�{��3�{��5�{�c�{��2n-1�{��2n+1����2�{��4�{��6�{�c�{��2n-2�{��2n
�����藧�B�@�@�i�؏I�j
�i�NjL�j�@�ߘa�T�N�U���X���t��
�@���܂����̐}�`���l�@���Ă���Ƃ��ɁA�ʔ����W��������ł��邱�ƂɋC�Â����B
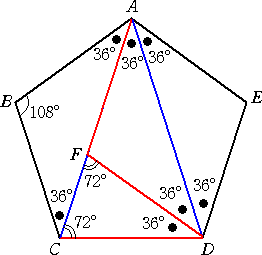 |
�@���T�p�`�̈�ӂ̒������Q�Ƃ���ƁA �@�@�`�e���e�c���b�c���Q�@�ł���B �@�����ŁA�e�b���w�Ƃ���ƁA��Ꭾ �@�@�@�Q�{�w�@�F�@�Q�@���@�Q�@�F�@�w �@�����藧���Ƃ���A�w�� �@�]���āA�`�b�� |
�@���̂Ƃ��A�@�Q�������R�U�����i![]() �{�P�j/�Q�@����A�@�������R�U�����i
�{�P�j/�Q�@����A�@�������R�U�����i![]() �{�P�j/�S�@�ł���B
�{�P�j/�S�@�ł���B
�܂��A���l�ɂ��āA�@�Q�������V�Q�����i![]() �|�P�j/�Q�@����A�@�������V�Q�����i
�|�P�j/�Q�@����A�@�������V�Q�����i![]() �|�P�j/�S�@�ł���B
�|�P�j/�S�@�ł���B
�@���̂��Ƃ���A�@�������R�U���E�������V�Q�����i![]() �{�P�j/�S�E�i
�{�P�j/�S�E�i![]() �|�P�j/�S���P/�S�@�ł���B
�|�P�j/�S���P/�S�@�ł���B
����ɁA�@�������R�U���|�������V�Q�����i![]() �{�P�j/�S�|�i
�{�P�j/�S�|�i![]() �|�P�j/�S���P/�Q�@�ł���B
�|�P�j/�S���P/�Q�@�ł���B
�@�܂��A
�@������2�R�U���{������2�V�Q�����i�������R�U���|�������V�Q���j2�{�Q�������R�U���E�������V�Q�����R/�S
�@������3�R�U���|������3�V�Q��
���i�������R�U���|�������V�Q���j3�{�R�������R�U���E�������V�Q���i�������R�U���|�������V�Q���j���P/�Q
�Ȃǂ����藧�B
�@�v�Z���ʂ����ׂėL�����ɂȂ�Ƃ����_���������B�����̔ѓ����i���Ɍ����A�u�����
�āA�X�S���Ȃ��ł����`�B�v�ƂȂ�̂��ȁH
�i�R�����g�j�@��̓I�� �������R�U���₃�����V�Q���̒l�����߂Ȃ��Ă��A
�@�������R�U���~�������V�Q�����P/�S
�ł��邱�Ƃ́A��}���疾�炩���낤�B
�@���ۂɁA�`�b�̒��_���l�Ƃ��A�l����ӂb�c�ɐ��������낵�A���̑����m�Ƃ����ƁA
�@�l�b���Q�������R�U���A�b�m���l�b�E�������V�Q���Ȃ̂ŁA�@�b�m���Q�������R�U���E�������V�Q��
�@�Ƃ���ŁA�b�m���P/�Q�@�Ȃ̂ŁA�@�������R�U���E�������V�Q�����P/�S�@�ł���B
�@�@�@�ȉ��A�H����