
あるものをある条件(数量の差や倍数関係)で、いくつかの部分に分ける問題は分配算と
言われる。
例えば、最も易しい分配算として、
1000円をA、Bの2人で分ける。AがBよりも400円多いとき、A、Bの持ち分を求
めよ。
を考えるとき、 1000÷2±200=700、300 とすれば、直ちに解が求められる。
線分図の考え方を用いれば、 (B+400)+B=1000 から、 B=300、A=700
としても求められる。
(追記) 令和4年7月25日付け
上記の問題で、1000−400=600(円) がBの持ち分の2倍なので、Bの持ち分は、
300円で、Aの持ち分は、700円とした方が実践的かもしれない。
このような考え方をいくつか練習しよう。
問題 40枚の色紙をA、B、Cの3人で分けると、BはAの3倍より6枚少なく、CはAの2倍
より4枚多いという。A、B、Cの3人の持ち分を求めよ。
(解) 40+6−4=42(枚) は、Aの持ち分の6倍なので、Aの持ち分は、7枚
このとき、Bの持ち分は、 15枚 、Cの持ち分は、 18枚 (終)
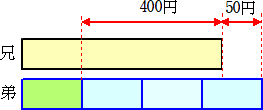
問題 兄の所持金は弟の所持金の4倍より50円少なく、兄と弟の所持金の差は、400円
であるという。兄と弟の所持金をそれぞれ求めよ。
(解) 弟の所持金の3倍は、 50+400=450(円) なので、弟の所持金は、150円
兄の所持金は、 550円 (終)
(コメント) 上記の問題は、次の線分図を考えれば納得できるだろう。
問題 85枚のカードをA、B、Cの3人で分けると、BはAの3倍、CはBより6枚少ないという。
Aは何枚のカードをもらったか?
(解) 85+6=91(枚) は、Aのもらったカードの7倍に相当するので、Aは、13枚もらっ
た。 (終)
問題 3つの整数A、B、Cに対して、 A÷B=22 ・・・ 6 、C÷B=4 ・・・ 5 で、
A+B+C=200 という。このとき、Aの値を求めよ。
(解) 200−6−5=189 は、27Bに相当するので、 B=7
よって、 A=22×7+6=160 である。 (終)
(追記) 令和4年7月26日付け
問題 3つの整数A、B、Cに対して、 A÷B=4 ・・・ 2 、B÷C=3 ・・・ 0 で、
A+B+C=146 という。このとき、Aの値を求めよ。
(解) A÷C=12 ・・・ 2 で、146−2=144 は、16Cに相当するので、 C=9
よって、 A=12×9+2=110 である。 (終)
問題 兄の所持金は弟の所持金の2倍より500円多く、兄と弟の所持金の和は、5000円
であるという。兄と弟の所持金をそれぞれ求めよ。
(解) 題意より、弟の所持金の3倍は、 5000−500=4500(円) なので、弟の所持金
は、1500円 よって、兄の所持金は、3500円 (終)
問題 3つの整数A、B、Cに対して、 B÷A=3 ・・・ 6 、(C+4)÷A=2 ・・・ 0 で、
A+B+C=98 という。このとき、Aの値を求めよ。
(解) 98−6+4=96 は、6Aに相当するので、 A=16 (終)
以下、工事中!
もう少し問題をレベルアップしよう。
問題 1000円を3人A、B、Cに分ける。AがBの3倍より700円少なく、BがCの2倍より
200円多いという。Aの持ち分はいくらか。
(解) B=2C+200 なので、 A=3B−700=6C−100
よって、 (6C−100)+(2C+200)+C=9C+100=1000 より、 C=100
このとき、 A=500 、B=400 、C=100 (終)
分配算はまた、やりとり算とも言われる。互いにものをやりとりするからである。
問題 A、B、Cの3人が最初にいくらかのお金を持っている。今、Aが所持金の半分をB
にあげ、次に、BがCに所持金から500円をあげ、最後に、CがAに所持金から700
円をあげたところ、A、B、Cの所持金がそれぞれ900円、800円、600円となった。
A、B、Cの最初の所持金はそれぞれいくらか。
(解) A÷2+700=900 より、 A=400
B+200−500=800 より、 B=1100
C+500−700=600 より、 C=800 (終)
容器の液体を交互に少しずつ入れ替えるという問題は、パズルとして正統派だろう。
(→ 参考:「意外な実験」)
2つの容器A、Bに同種の液体がそれぞれ異なった量ずつ入っている。次の操作を行う。
(1) Aの液体の1/3をBに移す。
(2) Bの液体の1/3をAに移す。
この操作の結果、A、Bの液体の量は何れも4リットルになった。
初めに各容器にはそれぞれどれだけの液体が入っていたか。
(解) 初めにA、Bに入っている液体の量をx、yとおく。
操作(1)により、A、Bに入っている液体の量は、それぞれ (2/3)x、y+(1/3)x
操作(2)により、A、Bに入っている液体の量は、それぞれ
(2/3)x+(1/3)(y+(1/3)x)=(7/9)x+(1/3)y
(2/3)(y+(1/3)x)=(2/9)x+(2/3)y
題意より、 (7/9)x+(1/3)y=4 、(2/9)x+(2/3)y=4
すなわち、 7x+3y=36 、2x+6y=36
この連立方程式を解いて、 12x=36 より、 x=3 で、y=5 (終)
連立方程式を解けば解が求まるが、解法としては美しくない。算数的に解いてみよう。
(別解) 操作(2)により、A、Bに入っている液体の量がそれぞれ4、4ということは、操
作(2)を行う直前のA、Bに入っている液体の量は、 2 、6 である。
実際に、操作(2)を行う直前のA、Bに入っている液体の量を、それぞれ a、b とおくと、
操作(2)により、 a+(1/3)b 、(2/3)b となる。
よって、 (2/3)b=4 から、 b=4÷(2/3)=6 で、
a=4−(1/3)・6=2 となる。
操作(1)の結果、A、Bに入っている液体の量がそれぞれ 2、6 なので、上記と同様
に考えて、 x=2÷(2/3)=3 で、 y=6−(1/3)・3=5 となる。 (終)
(x+y=8 を利用してもよい)
行列を利用すると、機械的に計算が進められるだろう。
操作(1)を表す行列Pは、
操作(2)を表す行列Qは、
なので、操作(1)(2)を表す行列PQは、
となる。その逆行列は、
よって、
から、初めにA、Bに入っていた液体の量は、3リットル、5リットル となる。
問題をもう少しレベルアップしよう。
問題 3つの容器A、B、Cに同種の液体がそれぞれ異なった量ずつ入っている。次の操
作を行う。
(1) Aの液体の半分を2等分して、それぞれ BとCに移す。
(2) Bの液体の半分を2等分して、それぞれ CとAに移す。
(3) Cの液体の半分を2等分して、それぞれ AとBに移す。
この操作の結果、A、B、Cの液体の量は何れも8リットルになった。
初めに各容器にはそれぞれどれだけの液体が入っていたか。
(解) 初めにA、B、Cに入っている液体の量をx、y、zとおく。
操作(1)により、A、B、Cに入っている液体の量は、それぞれ
(1/2)x 、y+(1/4)x 、z+(1/4)x
操作(2)により、A、B、Cに入っている液体の量は、それぞれ
(1/2)x+(1/4)(y+(1/4)x)=(9/16)x+(1/4)y
(1/2)(y+(1/4)x)=(1/8)x+(1/2)y
z+(1/4)x+(1/4)(y+(1/4)x)=(5/16)x+(1/4)y+z
操作(3)により、A、B、Cに入っている液体の量は、それぞれ
(9/16)x+(1/4)y+(1/4)((5/16)x+(1/4)y+z)=(41/64)x+(5/16)y+(1/4)z
(1/8)x+(1/2)y+(1/4)((5/16)x+(1/4)y+z)=(13/64)x+(9/16)y+(1/4)z
(1/2)((5/16)x+(1/4)y+z)=(5/32)x+(1/8)y+(1/2)z
題意より、 (41/64)x+(5/16)y+(1/4)z=8
(13/64)x+(9/16)y+(1/4)z=8
(5/32)x+(1/8)y+(1/2)z=8
すなわち、
41x+20y+16z=512 、13x+36y+16z=512 、5x+4y+16z=256
z を消去して、 7x−4y=0 、x+4y=32
この連立方程式を解いて、 8x=32 より、 x=4 で、y=7 、z=13 (終)
方程式を立てれば必ず解けるが、結構大変である。これも逆算で求めた方が楽でしょう。
A:8 、B:8 、C:8
操作(3)の実行 ↑
A:4 、B:4 、C:16
操作(2)の実行 ↑
A:2 、B:8 、C:14
操作(1)の実行 ↑
A:4 、B:7 、C:13
以上から、初めにA、B、Cに入っていた液体の量は、それぞれ
4リットル、7リットル、13リットル
である。
読者のために練習問題を残しておこう。(令和4年4月30日付け)
練習問題 3つの容器A、B、Cに同種の液体がそれぞれ異なった量ずつ入っている。次
の操作を行う。
(1) Aの液体の1/4をBに移す。
(2) Bの液体の1/4をCに移す。
(3) Cの液体の1/4をAに移す。
この操作の結果、A、B、Cの液体の量は何れも9リットルになった。
初めに各容器にはそれぞれどれだけの液体が入っていたか。
(解)
A:9 、B:9 、C:9
操作(3)の実行 ↑
A:6 、B:9 、C:12
操作(2)の実行 ↑
A:6 、B:12 、C:9
操作(1)の実行 ↑
A:8 、B:10 、C:9
以上から、初めにA、B、Cに入っていた液体の量は、それぞれ
8リットル、10リットル、9リットル
である。 (終)
さらに、問題を続けよう。今度は5人の場合である。
問題 5人の兄弟A、B、C、D、Eで、たくさんある金貨を、次のように分配した。
まず、Aが81枚、残り4人は、81>B>C>D>E となるように金貨を受領した。
そして、次のような操作を行った。
操作(1) Aは、他の4人の持ち分が2倍になるように自分の持ち分から金貨を分け与える。
操作(2) Bは、他の4人の持ち分が2倍になるように自分の持ち分から金貨を分け与える。
操作(3) Cは、他の4人の持ち分が2倍になるように自分の持ち分から金貨を分け与える。
操作(4) Dは、他の4人の持ち分が2倍になるように自分の持ち分から金貨を分け与える。
操作(5) Eは、他の4人の持ち分が2倍になるように自分の持ち分から金貨を分け与える。
以上の操作(1)〜(5)の結果、5人の持ち分は同じになったという。
初めに金貨は何枚あって、それを5人の兄弟A、B、C、D、Eはどのように受領したのだ
ろうか。
これも逆算により簡便に求められる。
(解) 全体を1とする。
A:1/5 、B:1/5 、C:1/5 、D:1/5 、E:1/5
操作(5)の実行 ↑
A:1/10 、B:1/10 、C:1/10 、D:1/10 、E:3/5
操作(4)の実行 ↑
A:1/20 、B:1/20 、C:1/20 、D:11/20 、E:3/10
操作(3)の実行 ↑
A:1/40 、B:1/40 、C:21/40 、D:11/40 、E:3/20
操作(2)の実行 ↑
A:1/80 、B:41/80 、C:21/80 、D:11/80 、E:3/40
操作(1)の実行 ↑
A:81/160 、B:41/160 、C:21/160 、D:11/160 、E:3/80
最初にAは81枚だったので、金貨の総数は160枚となる。
このとき、Bは41枚、Cは21枚、Dは11枚、Eは6枚 となる。 (終)
読者のために練習問題を残しておこう。市川学園中学の入試問題(2017)の改題です。
練習問題 2000円を、A、B、C、D の4人で分配する。もらう順番と配分(100円硬貨単
位で分配し、金額はそれぞれ異なり、かつ、それぞれもらう金額は200円以上)
はあみだくじで決めた。金額をもらうとき、4人は次のように発言した。
A:残りの1/3をもらった。
B:残りの1/4をもらった。
C:Bより、もらった金額は少なかった。
D:残り全部もらった。
さて、このとき、Cはいくらもらったのだろうか?
(解) 4人の発言から、最後にもらったのはDで、CはBの後にもらったことが分かる。
起こり得る可能性は、 A→B→C→D、B→A→C→D、B→C→A→D の3通り
まず、A→B→C→Dの場合
A:2000×1/3 は、「100円硬貨単位で分配」に矛盾し、この場合は起こり得ない。
次に、B→A→C→Dの場合
B:2000×1/4=500
A:1500×1/3 は、「100円硬貨単位で分配」に矛盾し、この場合は起こり得ない。
最後に、B→C→A→Dの場合
B:2000×1/4=500
残り1500円のうち、Cがもらえる金額の可能性は、200円、300円、400円
C:200 のとき、 A:1300×1/3 で、「100円硬貨単位で分配」に矛盾
C:300 のとき、 A:1200×1/3=400 で、 D:800 これは、起こり得る。
C:400 のとき、 A:1100×1/3 で、「100円硬貨単位で分配」に矛盾
以上から、Cがもらった金額は、 300円 (終)
次は、愛光中学の入試問題(2008)の改題です。
練習問題 A、B、Cの3人がいくらかずつお金を持っている。Aの所持金を2倍するとBの
所持金の3倍より180円多くなり、Bが所持金の1/4をCにあげたとしてもBはC
より60円多いという。
このとき、Aの所持金とB、C2人の所持金の合計では、どちらがいくら多いか?
また、3人の所持金の合計が930円のとき、Cの所持金はいくらか?
(解) 2A=3B+180 より、 A=(3/2)B+90
(3/4)B=C+(1/4)B+60 より、 C=(1/2)B−60 なので、 B+C=(3/2)B−60
よって、 A−(B+C)=90+60=150 なので、Aの所持金の方が150円多い。
また、A+B+C=3B+30=930 より、 B=300
このとき、 C=150−60=90 で、 A=450+90=540 (終)
分配算は、中学入試では頻出の分野である。もう少し、問題を練習しておこう。
問題 2つの整数があり、その和が300で、大きい方の数を小さい方の数で割ると商が
6で、余りが27になるという。このとき、2つの整数を求めよ。
(解) 題意より、 {(小さい数)×6+27}+(小さい数)=300 なので、
(小さい数)×7=273 から、 (小さい数)=39 で、
(大きい数)=300−39=261 (終)
問題 A、B、Cの3人がそれぞれいくらかずつ支払った。Aの払った金額はBの2倍で、そ
の後Bは、Aに400円、Cに300円払ったところ、3人の支払額が同じになったという。
A、B、Cの3人が初めに支払った金額はそれぞれいくらか。
(解) 題意より、 B−400=400+300 なので、 B=1100 、A=2200
C−300=1100+400+300 より、 C=2100
以上から、A、B、Cの3人が初めに支払った金額はそれぞれ
2200円 、1100円 、2100円
である。 (終)
(追記) 令和4年5月8日付け
次の問題は、支払い方法が斬新ですね!
問題 A、B、C、Dの4人がお金を出し合った。まず、Aは全体の1/3を支払い、次に、B
は他の3人(A、C、D)が出したお金の1/2、Cは、他の3人(A、B、D)が出したお金
の1/3を支払い、その結果、Dの支払う金額は60円となった。
果たして、4人全体で支払った金額はいくらであるか。
(解) 4人全体で支払った金額をTとおくと、題意より、
A=T/3 、B=(T−B)/2 、C=(T−C)/3 、D=60
このとき、 B=T/3 、 C=T/4 なので、
T=A+B+C+D=(11/12)T+60 から、 T=720
よって、4人全体で支払った金額は、720円である。 (終)
次は、溶液の配分の問題です。
問題 2つの容器A、Bがあり、AにはBの2倍の溶液が入っている。Aから30リットル、B
から20リットルを注ぎだしたところ、AにはBの3倍の溶液が入っていることになった。
初めに、A、Bの容器にはどれだけ溶液が入っていたか。
(解) 題意より、 A=2B 、 A−30=3(B−20) なので、
2B−30=3B−60 より、 B=30 よって、A=60 (終)
(追記) 令和4年5月21日付け
武蔵中学の入試問題(2014)です。一部改題しました。
問題 Aの所持金はBの3倍である。今、Aが所持金の1/2より480円多い金額をBにあ
げた。その後、Bがそのときの所持金の1/3の金額をAに戻したところ、2人の所持
金は等しくなった。Aの初めの所持金はいくらであったか。
(解) A=3B で、A→B の金額は、 (3/2)B+480 なので、
Bの所持金は、 B+((3/2)B+480)=(5/2)B+480 に増えた。
次に、 B→A の金額は、 (1/3)((5/2)B+480)=(5/6)B+160 なので、
Aの所持金は、 3B−((3/2)B+480)+((5/6)B+160)=(7/3)B−320
また、Bの所持金は、 (5/2)B+480−((5/6)B+160)=(5/3)B+320
題意より、 (7/3)B−320=(5/3)B+320 となるので、 B=960
このとき、 A=960×3=2880 となる。
よって、Aの初めの所持金は、2880円である。 (終)
上記の問題を逆算で求めてみよう。
(別解) 問題の操作で、2人の所持金がともに a 円になったとすると、
a a
B→Aの操作↑
(1/2)a (3/2)a
A→Bの操作↑
a+960 a−960
よって、題意より、 a+960=3(a−960) なので、 a=1920
以上から、Aの初めの所持金は、1920+960=2880(円) である。 (終)
(追記) 令和4年6月6日付け
甲と乙がそれぞれの所持金について話し合っていた。
甲:「私に800円くれれば、私の所持金は君の2倍になるね。」
乙:「君は私よりたくさん持っているんだから、君こそ私に800円くれよ。そうすれば、私と
君の所持金は同じになるんだから。」
さて、甲と乙の所持金は、それぞれいくらか?
(解) 甲+800=2(乙−800) より、 甲=2乙−2400
甲−800=乙+800 より、 甲=乙+1600
よって、 2乙−2400=乙+1600 より、 乙=4000 で、甲=5600 (終)
線分図を用いれば、文字を使わないで解くことができる。

上図から、
甲の所持金は、 (800×4)×2−800=5600(円)
乙の所持金は、 800×4+800=4000(円)
である。
以下、工事中!