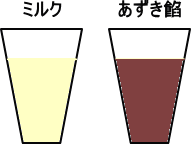
がある。ミルクとあずき餡は同量とする。
いま、ミルクの入った容器からスプーン一杯を取り出し、
それをあずき餡の容器に入れて、よくかき混ぜる。
その後、今度は、あずき餡の入った容器から、スプーン
一杯を取り出し、ミルクの容器に入れる。
 |
左図のように、それぞれミルクとあずき餡の入った容器 がある。ミルクとあずき餡は同量とする。 いま、ミルクの入った容器からスプーン一杯を取り出し、 それをあずき餡の容器に入れて、よくかき混ぜる。 その後、今度は、あずき餡の入った容器から、スプーン 一杯を取り出し、ミルクの容器に入れる。 |
このとき、ミルクの容器の中のあずき餡の量と、あずき餡の容器の中のミルクの量では、
どちらが多いだろうか?
この問題を初めて見た人にとっては、きっと、「ミルクの方が多い?」、いや、「あずき餡の
方が多い?」と悩むことだろう。私自身もそうだった。実は、答えは「同じ!」なのである。
次のように考えると、明らかである。
最初に、ミルクとあずき餡がそれぞれスプーン2杯分入っているものとする。このとき、
| 初期状態 | 1回目の移動 | 2回目の移動 | |
| ミルクの容器 | ミルク 2杯分 | ミルク 1杯分 | ミルク 4/3杯分 +あずき餡 2/3杯分 |
| あずき餡の容器 | あずき餡 2杯分 | あずき餡 2杯分 +ミルク 1杯分 |
あずき餡 4/3杯分 +ミルク 2/3杯分 |
以上の計算から、確かに両者の量は同じである。この関係は、両者を何倍しても変わら
ない。
(参考文献:E.P.ノースロップ 著 松井政太郎 訳 ふしぎな数学(みすず書房))
上記では分数計算をして問題を解いたが、次のように図式化すると分かりやすい。
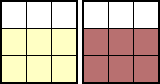 |
→ | 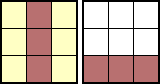 |
→ | 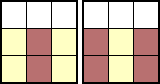 |
この操作をもう1回やったらどうなるだろうか?興味があったので実験してみた。
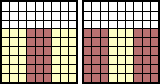 |
→ | 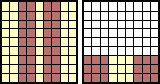 |
→ | 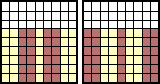 |
ミルクの容器のあずき餡の量は、 0 → 1/3 → 4/9 → ・・・ と移り変わる。
だんだんと、1/2 に収束するような...予感。(当たり前か!)
漸化式を使って、計算してみよう。
上記の操作を、n 回行った後のミルクの容器のミルクとあずき餡の量をそれぞれ、an 、
bn とおく。このとき、あずき餡の容器のミルクとあずき餡の量はそれぞれ、bn 、an と
なる。 また、 a0 =1 、b0 =0 である。
漸化式 an+1=(2/3){(1/2)bn+an}=(2/3)an+(1/3)bn
bn+1=(2/3){(1/2)an+bn}=(1/3)an+(2/3)bn
が成り立つので、bn を消去して、 3an+2−4an+1+an=0、a0 =1 、a1 =2/3
これより、 an+2−(1/3)an+1=an+1−(1/3)an から、 an+1−(1/3)an=1/3
an+2−an+1=(1/3){an+1−an} から、 an+1−an=(1/3)n(−1/3)=−(1/3)n+1
よって、 an=(1/2){1+(1/3)n} となり、同様にして、 bn=(1/2){1−(1/3)n}
このことから、 n → ∞ のとき、確かに、 an → 1/2 、 bn → 1/2 である。
(参考文献: 吉永良正 著 数学のセンス (ダイヤモンド社))
(追記) 平成20年9月18日付け
冒頭の問題では、液体の量が明示されていないので、多少レベルが高いが、次のように
具体的に問題設定がなされていれば計算してみようという気にもなるだろう。
焼酎0.5リットル入った容器Aとお湯1.5リットル入った容器Bがある。まず、Aか
ら0.1リットルをBに移し、よくかき混ぜて逆に今度はBから0.1リットルをAに戻す。
このとき、Aにおけるお湯の割合とBにおける焼酎の割合はどちらの方が多いだろ
うか?
この操作を繰り返すとき、Bにおける焼酎の濃度はだんだん高くなるが、何%に近
づくだろうか?
答えは、もちろん同じ割合で、操作を続けると、25%に近づく。
(コメント) 後半の問いかけが、目新しいですね!
(追記) 令和6年11月16日付け
冒頭の問題と同趣旨の問題が、東北大学 文系(1985)で出題された。
問題 濃度a%の食塩水6Lが入っている容器Aと、濃度b%の食塩水4Lが入っている容
器Bがある。Aより1Lの食塩水をとって、それをBにうつし、よく混ぜ合わせた後に同量を
Aに戻すものとする。この操作を k 回くり返したときのA、Bの食塩水の濃度をそれぞれ
ak%、bk%とする。
(1) bk−ak はどのような数列となる。.
(2) ak、bk を求めよ。
(解)(1) Aより1Lの食塩水をとって、それをBにうつすと、食塩 1000・a/100=10a(g)
がBに移る。
そのとき、Aに残る食塩の量は、6000・a/100−1000・a/100=50a(g)
Bに含まれる食塩の量は、 4000・b/100+10a=10a+40b(g) となる。
このとき、濃度 b1 は、 b1=(10a+40b)/5000・100=(a+4b)/5(%)
次に、Bより1Lの食塩水をとって、それをAにうつすと、
食塩 1000・(a+4b)/500=2a+8b(g)
がAに移る。このとき、濃度 a1 は、
a1=(2a+8b+50a)/6000・100=(13a+2b)/15(%)
これより、一般に、a=a0 、b=b0 として、
ak+1=(13ak+2bk)/15(%) 、bk+1=(ak+4bk)/5(%)
よって、 bk+1−ak+1=(2/3)(bk−ak) から、
bk−ak は、初項 b−a で、公比 2/3 の等比数列となる。
したがって、 bk−ak=(b−a)・(2/3)k
(2) ak+1=(13ak+2bk)/15 より、
ak+1−ak=(2/15)(bk−ak)=(2/15)(b−a)・(2/3)k
すなわち、 ak−ak-1=(2/15)(b−a)・(2/3)k-1
ak-1−ak-2=(2/15)(b−a)・(2/3)k-2
・・・・・・・・・・・・・・・
a1−a=(2/15)(b−a)・1
より、 k≧1 のとき、
ak−a=(2/15)(b−a)・(1+(2/3)+・・・+(2/3)k-1)=(2/5)(b−a)・(1−(2/3)k)
よって、
ak=a+(2/5)(b−a)・(1−(2/3)k)=(3a+2b)/5−(2/5)(b−a)・(2/3)k
この式は、k=0 のときも成り立つ。
また、bk−ak=(b−a)・(2/3)k より、
bk=ak+(b−a)・(2/3)k
=(3a+2b)/5−(2/5)(b−a)・(2/3)k+(b−a)・(2/3)k
=(3a+2b)/5+(3/5)(b−a)・(2/3)k (終)
(コメント) 食塩水の濃度の問題は、食塩量に着目するのがポイントですね!
以下、工事中!
