
数学では、問題解決のために図を書くことが多い。このページでは、特に、線分図につい
てまとめておこうと思う。線分図とは、同じ量を同じ長さの線分で表した図のことを言う。
線分図は、問題の状況を視覚的に把握するための有用な道具である。線分図が如何に
有用であるかは、例えば、「比の計算の妙」を見れば明らかだろう。
例題1 連続する9個の整数を全て足すと、1800になるという。9個のうちで一番大きい整
数を求めよ。
(解) 連続する9個の整数は、
x−4、x−3、x−2、x−1、x、x+1、x+2、x+3、x+4
とおける。よって、その和は、9x となり、題意より、 9x=1800 から、x=200
よって、9個のうちで一番大きい整数は、 200+4=204 である。 (終)
文字を使い方程式を立てれば何でもない問題であるが、この問題を、線分図で解いてみ
よう。
(別解)
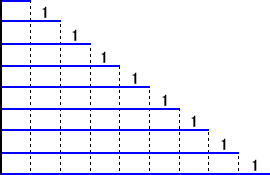
上図から、最小の整数は、 {1800−(1+2+3+4+5+6+7+8)}÷9=196
よって、9個のうちで一番大きい整数は、 196+8=204 である。 (終)
例題2 A、B2人合わせて1000円持っている。Aの持っているお金は、Bより140円多い。
Bはいくら持っているか。
(解) (B+140)+B=1000 から、 B=430 (終)
線分図がイメージできれば、暗算でも計算可能だろう。
(別解)
上図より、 (1000−140)÷2=430 (終)
例題3 195人の生徒をA、B、C、Dの4組に分ける。DはAより5人多く、CはBより6人少
ない。AはBより8人多い。人数の最も多い組は何人の生徒がいるか。
(解)
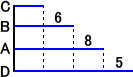
上図より、 (195+6+8×2+5×3)÷4=232÷4=58(人) (終)
例題3 84個のりんごを6人の子供に配る。受け取るりんごの個数は全て異なり、最も多く
受け取る人のりんごの個数を出来るだけ少なくしたい。最も多く受け取る人のりんご
の個数を求めよ。
(解)
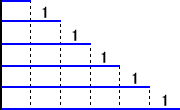
題意より、とりあえず差が1と考えると、
(84+1+2+3+4+5)÷6=99÷6=16・・・3
余り3は上位3人に配ることにして、最も多く受け取る人のりんごの個数は、17個 (終)
(コメント) 線分図の活用は、どことなく鶴亀算の発想に似ていますね!
(追記) 令和4年4月29日付け
例題4 父親がお年玉を3人の子供A、B、Cに次のように与えた。
BはAの2/3より2000円少なく、CはAの1/4より1000円多い。3人がもらったお年玉の
合計額が22000円のとき、3人A、B、Cはいくらもらったでしょう。
(解) BはAの8/12、CはAの3/12 とすると、3人合わせて、1+8/12+3/12=23/12
これが22000+2000−1000=23000(円)に相当するので、
A:12000円 、B:6000円 、C:4000円
となる。 (終)
線分図を用いれば、次のような別解も考えられる。
(別解)
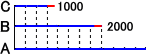
(1/12)A=a とおくと、 (3+8+12)a=22000−1000+2000=23000
すなわち、 23a=23000 より、 a=1000
よって、 A=12a=12000 、B=8a−2000=6000 、C=3a+1000=4000
(終)
読者のために練習問題を残しておこう。海星女子中学の入試問題(2012)の改題です。
練習問題 A、B、Cの3人の所持金の合計は、1770円である。AはBより250円多く、
BはCより130円多い。A、B、Cのそれぞれの所持金はいくらか。
(解)
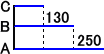
C+(C+130)+(C+130+250)=1770 より、 3C=1260 よって、C=420
このとき、 B=420+130=550 、A=550+250=800 (終)
(コメント) 算数的には、 C=(1770−250−130×2)÷3=420 とするのかな?
以下、工事中!