える。そんな爽やかな経験を是非若いうちに十分しておきたいものだ。
問題タイプ別に分けたいくつかの問題を通して、比の計算の妙を味わっていただければと
思う。
(比の和が一定)
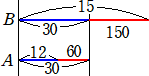
問題1 AとBの持っているお金の比は、6:1でしたが、AがBに200円あげたところ、持っ
ているお金の比は、4:3になりました。最初に2人が持っていた金額はいくらですか。
(解) 最初 A:B=6:1 A→Bの後、 A:B=4:3 と考えると、比の和
は一定なので、比の値の変化量2(=6−4=3−1)が200円に相当する。
よって、比1当たり100円なので、Aは600円、Bは100円持っていたことになる。 (終)
(追記) 令和2年3月17日付け
2020年度の洛星中学前期入試で、(比の和が一定)の問題が出題された。
問題1’ 兄と弟の所持金の比は13:11でしたが、兄が弟に867円渡すと、所持金の比は
3:13になりました。初めの兄の所持金はいくらでしょうか?
(解) 13:11=26:22 兄が弟に867円渡した結果、 3:13=9:39
比の和が一定なので、 26−9=17 が867円に相当する。
すなわち、比1あたり 51円 なので、初めの兄の所持金は、
51×26=1326(円) (終)
(比の差が一定)
問題2 AとBの持っているお金の比は、4:3でしたが、お年玉で200円ずつもらったので、
比が5:4になりました。最初に2人が持っていた金額はいくらですか。
(解) 最初 A:B=4:3 A+200、B+200の後、 A:B=5:4 と考えると、比の差
は一定なので、比の値の変化量1(=5−4=4−3)が200円に相当する。
よって、Aは800円、Bは600円持っていたことになる。 (終)
問題3 飴の入った箱A、Bがあり、両方に20個加えたら、個数の比が3:1となり、続けて
さらに40個加えたら個数の比が7:4となった。初めの個数は何個ずつだったか?
(解) 箱A、Bに入っている個数の差は一定で、両方に20個加えたら、A:B=3:1=9:3
さらに40個加えたら、A:B=7:4=14:8
比5(=14−9=8−3)当たり40なので、比1当たり8
よって、20個加えたとき、 Aは72個、Bは24個なので、最初に入っていたのは、
Aは52個、Bは4個 (終)
問題4 男:女=5:3 のとき、男女とも10人入ると、男:女=10:7 となった。
現在の男女数は?
(解) 差が一定なので、 男:女=5:3=15:9 男+10、女+10 の後、
男:女=10:7=20:14
比5(=20−15=14−9)当たり10なので、比1当たり5
現在の男=100、女=70 なので、社員数は、170人 (終)
問題5 Aの水槽に200リットル、Bの水槽に100リットルの水が入っている。両方の水槽
から同じ量の水を汲み出す。Aの残り:Bの残り=3:1のとき、Bには何リットル残っ
ているか?
(解) Aの水槽とBの水槽の差は、100リットルで、これは変わらない。
比2(=3−1)当たり、100リットルなので、比1当たり50リットル。
よって、Bの水槽には、50リットル残っている。 (終)
(一方が固定)
問題6 AとBの持っているお金の比は、4:1でしたが、Bが300円もらったので、比が5:2
になりました。最初に2人が持っていた金額はいくらですか。
(解) 最初 A:B=4:1=20:5 B+300の後、 A:B=5:2=20:8 と考えると、
比の値の変化量3(=8−5)が300円に相当する。
よって、比1当たり100円なので、Aは2000円、Bは500円持っていたことになる。 (終)
(和が一定)
問題7 A、B、Cの3人の所持金の比は、5:4:1でしたが、AがCに300円あげたので、そ
の比は、7:8:5になりました。最初に、A、B、Cはいくら持っていましたか。
(解) A:B:C=5:4:1=10:8:2 A→Cの後、 A:B:C=7:8:5 と考えると、比の値
の変化量3(=10−7=5−2)が300円に相当する。
よって、比1当たり100円なので、Aは1000円、Bは800円、Cは200円持っていたこ
とになる。 (終)
(片方が増で残りが減であるとき)
問題8 AとBの持っているお金の比は、3:1でしたが、Aが5000円使い、Bが2500円他
よりもらったので、比が1:2になりました。最初に2人が持っていた金額はいくらです
か。
(解) 最初 A:B=3:1=6:2 A−5000、B+2500の後、 A:B=1:2 と考えると、
比の値の変化量5(=6−1)が5000×2+2500=12500円に相当する。
よって、比1当たり2500円なので、Aは7500円、Bは2500円持っていたことになる。
(終)
(別解) 最初にA、Bの持っているお金を、それぞれ3N、Nとすると、題意より、
3N−5000 : N+2500=1:2 より、N=2500
よって、 Aは7500円、Bは2500円持っていたことになる。 (終)
(両者がともに増または減のとき)
問題9 AとBの持っているお金の比は、5:4でしたが、Aが600円、Bが500円使ったの
で、残りの比が4:3になりました。最初に2人が持っていた金額はいくらですか。
(解) 最初 A:B=5:4=15:12 A−600、B−500の後、 A:B=4:3=16:12
と考えると、比の値の変化量1(=16−15)が500×4−600×3=200円に相当する。
よって、Aは1000円、Bは800円持っていたことになる。 (終)
(別解) 最初にA、Bの持っているお金を、それぞれ5N、4Nとすると、題意より、
5N−600 : 4N−500=4:3 より、N=200
よって、 Aは1000円、Bは800円持っていたことになる。 (終)
(コメント) 問題8、9はちょっと自信がなかったので、方程式を立てて計算してみました。
方程式を立てた方が明解かな?
問題8、9について、らすかるさんから別解をいただきました。(令和元年8月19日付け)
(問題8の別解)
Bの所持金と貰った金額を2倍すると、
所持金比3:2→AがBに5000円あげる→所持金比1:4
となり、問題1と同じ方法で、
比2(=3−1=4ー2)当たり5000円なので、比1当たり2500円となり、
A=7500円、B=5000円となる。
よって、答えは、Aが7500円、Bが5000÷2=2500円 (終)
(問題9の別解)
Aの所持金と使った金額を5倍、Bの所持金と使った金額を6倍すると、
所持金比25:24→両者3000円使う→所持金比10:9
となり、問題4と同じ方法で、
比15(=25−10)当たり、3000円なので、比1当たり200円
よって、A=5000円、B=4800円となるので、答えは、
Aが5000÷5=1000円、Bが4800÷6=800円 (終)
(コメント) なるほど!何倍かして金額を揃えるという手法もあるのですね。らすかるさんに
感謝いたします。
問題10 今、A、B2人の前にはお金が山のように積んである。1回目は2人は同じ金額を
取る。2回目は残りのお金をA:B=3:1になるように取ったところ、2人の金額は、
A:B=4:3になった。Aが1回目に取った金額と2回目に取った金額の比はどうな
るか?
(解) Aが1回目、2回目に取った金額をそれぞれ N、3n とおくと、A=N+3n 、B=N+n
このとき、A−B=2n が比1当たりとなる。すなわち、
A=N+3n=8n 、B=N+n=6n より、 N=5n
よって、Aが1回目に取った金額と2回目に取った金額の比は、5n:3n=5:3 となる。
(終)
問題10は分配算の問題であるが、(比の差が一定)の問題2と同様に解きうる。
(問題10の別解) 最初 A:B=3:1 A+N、B+Nの後、 A:B=4:3=8:6 と考え
ると、比の差は一定なので、比の値の変化量5(=8−3=6−1)がN円に相当する。
このとき、比1当たりN/5 となるので、 N → 3N/5 より、
Aが1回目に取った金額と2回目に取った金額の比は、 5:3 となる。 (終)
次は、年齢算の問題であるが、(比の差が一定)の問題2と同様に解きうる。
問題11 現在、父親は38歳、子供は5歳である。何年後に、父親の年齢が子供の年齢
の4倍になるか?
(解) 父親の年齢と子供の年齢の差は33歳で、これは何年経っても変わらない。
比3(=4−1)当たり33歳なので、比1当たり11歳。よって、父親の年齢が44歳のとき、
子供の年齢は11歳となり、題意を満たす。
よって、6年後に父親の年齢が子供の年齢の4倍になる。 (終)
(別解) 線分図を用いると解法も明解になるだろう。
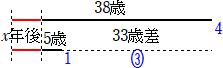 (終)
(終)問題11の類題です。
問題12 A、Bの年齢の比は4:1、14年後には5:3となる。現在のA、Bの年齢を求めよ。
(解) 2人の年齢の差は何年経っても変わらない。
A:B=4:1=8:2 14年後に A:B=5:3=15:9
比7(=15−8=9−2)当たり14 なので、比1当たり2
よって、Aの年齢が16歳、Bの年齢は4歳となる (終)
倍数算を線分図で解くためには、初めと後で変わらないものを見つける
問題13 A:B=2:3 Aに+10、Bから−30 の結果、A:B=5:6 となった。
初めの量を求めよ。
(解)