テープの裁断２ 
当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（平成２６年７月２６日付け）
１mのテープを、定規を使わずに１/３だけ切り取りたい。どのように切り取ればよいか。
（答） らすかるさんが考察されました。（平成２６年７月２６日付け）
文だと説明しにくいので絵で。固定点と固定された杭は実際は同一場所ということで．．．。
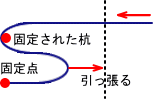引っ張って、右端が一致したら止める
DD++さんが考察されました。（平成２６年７月２７日付け）
テープを半分の半分の半分の半分に折り、１６等分の折り目をつけます。便宜上、端を０と
１６とし、折り目を順に、１、２、３、・・・、１５とします。０と１６をテーブル上の同じ場所に重ね
て押さえます。４を、０〜４間がピンと張るようにしてテーブルに抑えます。４〜９間と１３〜１６
間がピンと張るようにしたまま、９と１３を動かし、それらを同じ位置に重ねます。９を離し、
１３の位置が動かないように、１６-１３の線を１３方向に伸ばしていきます。限界まで引っ張っ
たときの頂点が端からちょうど１/３の点になっているので、そこで切れば完了です。
らすかるさんが考察されました。（平成２６年７月２７日付け）
DD++さんの方法を参考にして…。
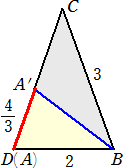
テープを半分・半分・半分に折り、８等分の折り目をつけます。端をA、Dとし、
AB ： BC ： CD ＝ ２ ： ３ ： ３ となる点をB、Cとして、DをAと合わせて三辺が、AB、BC、CD
である二等辺三角形を作ります。次に、辺ABをBを中心としてCに近づく方向に回転させ、A
が辺CD上に合ったとき、ADはテープの長さの１/６ですから、それを２倍すれば全体の１/３
になります。
（コメント） なるほど！８÷６＝４/３ で、
確かに、１/６が作られていますね。 |
 |
DD++さんからのコメントです。（平成２６年７月２７日付け）
ふと思ったのですが、ひもじゃなくテープってことは（無視できない）幅がある設定でしょうか？
だとすると私の方法は不成立になってしまいますね。
Ｓ（Ｈ）さんから参考資料を頂きました。（平成２６年７月２７日付け）
（コメント） 当ＨＰの次のページが参考になると思う。
紙を折る 折り紙を折る
与えられたテープをもう３本用意して、それらを周とした正方形を作る。この正方形に芳賀
の定理を適用すれば、１/３の長さは実現できるだろう。でも、やはり、らすかるさんの方法の
方が優れていると思う。
らすかるさんの手法は、「テープの裁断」の手法に通じるものがありますね！
よおすけさんからのコメントです。（平成２６年７月２７日付け）
らすかるさん、DD++さん、S(H)さん、ありがとうございます。この問題は、「テープの裁断」の、
いわば類題です。
１mのテープから１/３だけ切り取るというと、DD++さんの指摘の通り、「１mのテープから１/３
だけ切り取るは、『長さ』ではなく『幅』なのか？」も頭をかすめました。あえて、テープの幅は
設定していませんでしたが、２通り以上の解釈がされそうという恐れはありました。
DD++さんからのコメントです。（平成２６年７月２７日付け）
私の疑問はそうではなくて、「幅のあるテープを横に曲げるのは無理だなあ」という点でした。
ただ、よく考えればテープを机の上に立てるようにすればいいだけでしたね。私の方法は、テ
ープ同士の交差はさせませんし．．．。
やっぱり切り取るならこの比でしょう、ということで、類題です。
１本のテープがある。定規等の道具を使わずに黄金分割したい。どのようにすればよいか。
（コメント） １本のテープを対角線とする正５角形を作れば、
辺の長さ ： 対角線の長さ＝１ ： （１＋
）/２
と黄金比になるのだが．．．。（→ 参考：「意外なところに黄金分割」）
DD++さんから解答を頂きました。（平成２６年８月８日付け）
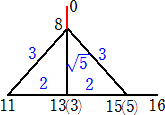
テープを半分の半分の半分の半分に折り、１６等分の折り目をつけます。便宜上端を 0 と
16 とし、折り目を順に、1、2、3、…、15 とします。16側の端を1区間分余らせ、15-11-8-5で
三角形を作ります。そのまま2周目に入り、3を13に重ねて押さえます。
線分3-0が点8と重なるようにピンと張ると、点8より向こう側にはみ出た分がテープ全体の
(3-√5)/16。よって、そこに新たな折り目を付け、その区間を8回分折り返したところで切ると、
(3-√5)/2 と (-1+√5)/2 に切ることになるので黄金分割できます。
（コメント） なるほど、巧妙な部分にが作られて、解決されますね！
