10cm四方の紙を三つ折りにして下さいと言われたら、おそらく直ぐに出来ると思う。しか
し、数学では、1は3で割り切れない。実際には出来るのに、数学では表せないのって、不
思議だなと思った。
(塾長よりコメント) 私は、「10cm四方の紙を三つ折りにして下さいと言われたら、直ぐ
に出来る」という点にむしろ感心した。
三つ折にも、「巻三つ折」と「外三つ折」があって、それぞれ折り方は違うようだ。「巻三つ
折」の場合、単純に3等分すると不具合が生じるので、完全な3等分では普通折らない。
したがって、Y.F氏のいう三つ折とは、「外三つ折」のことを指すのだろう。
折り紙と言えば、「芳賀の定理」と言うくらい次の定理は有名である。
芳賀の定理 正方形の紙を1枚取り出し、2つに折って、上辺の中点に印をつける。
その中点に下辺の右端の角を合わせた位置で紙を折る。
このとき、左辺に折り返した紙との重なり目ができる。
その重なり目、つまり辺の交点は左辺の三等分点の一つである。
この定理により、定規やコンパスなどを一切使わずに、正方形の折り紙を数学的に正確
に3等分することができる。
当HPでも以前にこの話題を取り上げた。( → 折り紙を折る)
是非参考にして下さい。
(追記) 令和6年5月3日付け
「10cm四方の紙を三つ折りにする」ことは、あまり実用的ではない。実用的なのは、
A4用紙を三つ折りにする
方だろう。
A4用紙のサイズは、210mm × 297mm で、縦297mm の3等分は、99mm である。
そこで、 297−210=87(mm) であることに着目すると、次のようにザックリと3等分
が可能である。
(1) A4用紙を2枚用意する。

(2) 2枚を縦横に重ねて、はみ出し部分を折る。
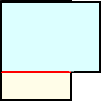
(3) 重なっている部分を2等分して折る。

このように折り目をつけると、 87mm 、105mm 、105mm と三つ折りが完成する。
厳密な三つ折りではないが、実用的には十分であろう。
