折り紙を折る　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

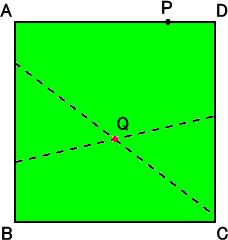　　　　　左のような正方形の形をした折り紙がある。

　　　　いま、辺ＡＤ上に任意に点Ｐをとり、次のように折
　　　　り紙を折る。

　　　　　頂点Ｂを点Ｐに重なるように折り、折り目をつけ
　　　　る。
　　　　　同様に、頂点Ｃを点Ｐに重なるように折り、折り
　　　　目をつける。

　　　　このときできる２つの折り目の交点Ｑは、互いに
　　　　折り目を２等分する。

　　　　これは、どうしてか？
































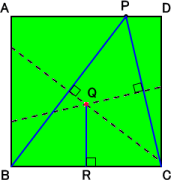
　（答）　次の図から明らかであろう。点Ｑは△ＰＢＣの外心である。

　　　　　　　　　　

　さらに、この折り紙には面白い性質がたくさん秘められているらしい。このことを、あるセミ
ナーの席で、横浜国立大学教育人間科学部の橋本吉彦先生から伺うことができた。

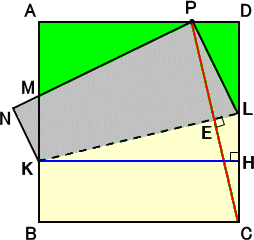　　　　左図のような１辺の長さが１の正方形ＡＢＣＤ
　　　において、ＰＤ＝Ｘ　とおく。
　　　　このとき、直角三角形ＰＤＬ　において、

　　　　　　　　　ＰＤ2＋ＤＬ2＝ＰＬ2

　　　よって、　Ｘ2＋(１−ＰＬ)2＝ＰＬ2　から、

　　　　　　　　　ＰＬ＝ＬＣ＝(１＋Ｘ2)/２

　　　また、　ＤＬ＝１−ＬＣ＝(１−Ｘ2)/２　である。

　　　ところで、△ＰＣＤ と △ＬＫＨ において、
　　　　　∠ＰＤＬ＝∠ＬＨＫ＝９０°

　　
　また、∠ＬＫＨ＋∠ＥＬＨ＝９０°、∠ＥＬＨ＋∠ＰＣＤ＝９０°より、　∠ＬＫＨ＝∠ＰＣＤ
よって、２角が等しいので、△ＰＣＤ ∽ △ＬＫＨ　が成り立つ。

　このとき、ＰＤ ： ＤＣ ＝ ＬＨ ： ＨＫ が成り立つので、Ｘ ： １ ＝ ＬＨ ： １ となる。
これより、　ＬＨ＝Ｘ　である。
　よって、ＫＢ＝ＮＫ＝ＨＣ＝１−Ｘ−(１−Ｘ2)/２＝(１−Ｘ)2/２

　また、△ＡＭＰ ∽ △ＤＰＬ より、ＡＭ ： ＡＰ ＝ ＤＰ ： ＤＬ が成り立つので、
　　　　ＡＭ ： １−Ｘ ＝ Ｘ ： (１−Ｘ2)/２
これより、
　　　　　　ＡＭ＝２Ｘ/(１＋Ｘ)　なので、ＭＢ＝１−２Ｘ/(１＋Ｘ)＝(１−Ｘ)/(１＋Ｘ)
が成り立つ。

　ここで、特に、

　　　Ｘ＝１/２ （即ち、点Ｐが辺ＡＤの中点）の場合を考えると、ＭＢ＝１/３ となる。

　この事実は、折り紙の世界では有名な「芳賀の定理」といわれているものである。

　折り紙の１辺の中点の作り方は容易であるが、１辺を３等分することは、それほど容易で
ない。しかし、この芳賀の定理を用いると、１辺を３等分することは容易となる。


　さらに、上記の長さの計算を活用すると、　ＡＢ＝２ＪＫ　であることがわかる。

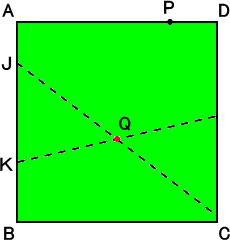　　　実際に、ＰＤ＝Ｘ　とおくと、

　　　　　　ＫＢ＝(１−Ｘ)2/２

　　　同様に、ＡＰ＝１−Ｘ に対して、

　　　　　　ＡＪ＝(１−(１−Ｘ)2)/２

　　　よって、

　　　　ＪＫ＝１−ＫＢ−ＡＪ＝１/２

　　　故に、ＪＫの長さは、ＡＢの長さの半分である。

　この事実は、次のように一般化できる。

定理　　横の長さが １、縦の長さが ａ （ａ＞１）の長方形の形をした折り紙を考える。
　 　　　いま、辺ＡＤ上に任意に点Ｐをとり、次のように折り紙を折る。


　　頂点Ｂを点Ｐに重なるように折り、折り目をつける。
　　同様に、頂点Ｃを点Ｐに重なるように折り、折り目を
　　つける。
　　　このとき、　　　ＡＢ＝２ａ2・ＪＫ　　が成り立つ。









　　証明は、上記と同様に行うことができるので、結果だけ述べることにする。

　　左図のおいて、ＰＤ＝Ｘ　とおく。

　　このとき、　ＰＬ＝ＬＨ＝(ａ2＋Ｘ2)/(２ａ)　なので、

　　　　ＤＬ＝(ａ2−Ｘ2)/(２ａ)

　　また、ＰＤ ： ＤＣ ＝ ＬＨ ： ＨＫ より、

　　　　　　　　　Ｘ ： ａ ＝ ＬＨ ： １

　　よって、　ＬＨ＝Ｘ/ａ　なので、

　　ＫＢ＝ＨＣ＝ａ−Ｘ/ａ−(ａ2−Ｘ2)/(２ａ)
　　　　　　　　＝(ａ2−１＋(１−Ｘ)2)/(２ａ)

　したがって、ＡＪ＝(ａ2−(１−Ｘ)2)/(２ａ)　なので、

　　　　　　　ＪＫ＝ａ−(ａ2−１＋(１−Ｘ)2)/(２ａ)−(ａ2−(１−Ｘ)2)/(２ａ)＝１/(２ａ)

ＡＢ＝ａ　なので、　　ＡＢ＝２ａ2・ＪＫ　　が成り立つ。

（注意）　Ａ版とかＢ版のような定型の紙の場合、ａ＝ なので、上記の操作を行うときで
　　　　　きる折り目について、ＪＫは、ＡＢの １/４ 倍である。


　また、次のような事実も面白い。

　下図のような、一辺の長さが １ の正方形 ＡＢＣＤ において、点Ｐは、辺ＡＤ上の任意の
点とする。　このとき、次が成り立つ。

　　線分ＭＮの長さは、△ＡＰＭ の内接円の半径に等しい。

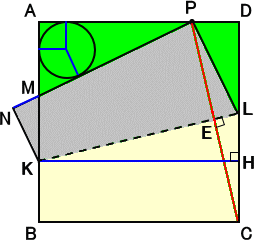　　　実際に、内接円の半径を ｒ とすると、
　　　　　　ＰＭ＝ＡＰ− ｒ ＋ＡＭ− ｒ
　　であるので、
　　　　　ｒ ＝(ＡＰ＋ＡＭ−ＰＭ)/２
　　ところで、ＰＤ＝Ｘ とおくと、
　　　ＡＰ＝ １−Ｘ　、ＡＭ＝ ２Ｘ/(１＋Ｘ)
　　なので、三平方の定理より、
　　　　　　ＰＭ ＝ (１＋Ｘ2)/(１＋Ｘ)
　　よって、
　　　　　　　ｒ ＝ Ｘ(１−Ｘ)/(１＋Ｘ)
　　　一方、
　　　　　　△ＡＰＭ ∽ △ＮＫＭ
　　　　　　ＮＫ＝ＫＢ＝(１−Ｘ)2/２
　　なので、
　　　　　　ＭＮ＝ＮＫ・ＡＭ/ＡＰ
　　　　　　　　 ＝Ｘ(１−Ｘ)/(１＋Ｘ)
　　したがって、
　　　　　　　　　　ＭＮ ＝ ｒ


　この問題は、算学定理として英文の数学雑誌にも掲載されたらしい。

　このように、たった１枚の折り紙であるが、そこには、非常に面白い数学的事象が隠れ
ていることに驚かされる。

　芳賀の定理を発見された元筑波大学教授の芳賀和夫先生は、研究の合間、気分転換
に折り紙で遊んでいて、いろいろと面白い事実に気づかれたそうだ。まだまだ身近には、
このような面白い事実が隠れているかと思うと、なぜかワクワクしてしまう。