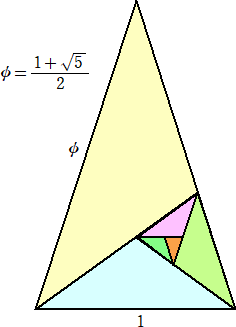意外なところに黄金分割 　　　　　　　　　　　　　　　　　　　

　「数学的な美しさ」というと、昔から言及されるのが「黄金分割」という見方・考え方である。
比の美しさというのは全く主観的なものとはいえ、古来多くの黄金分割が我々の目に届く。

　今、一つの線分を２つに分けることを考える。

　

このとき、　ｍ　：　ｎ　＝　ｍ＋ｎ　：　ｍ　であるように分けると美しいと言われている。

このような分割の仕方が黄金分割である。

　最初に、このような分割を定義したのは、ユークリッド（紀元前３２５年〜紀元前２６５）で、
黄金分割（ｓｅｃｔｉｏ　ａｕｒｅａ）と命名したのは、レオナルド・ダ・ヴィンチだと言われる。

　出版物で初めて黄金分割という言葉が用いられたのは、マルティン・オームの「初等純粋
数学」（１８８５年）であるらしい。

　上記の比例式から、　ｍ²−ｍｎ−ｎ²＝０　が成り立ち、比 ｍ/ｎ の値は、

　

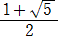
となる。このおおよその値は、１．６１８　である。この比のことを、黄金比という。

　この神秘的な比のことは、黄金比以外に、神聖比とか、黄金平均とか、黄金数とか呼ばれ、
記号ではギリシャ語の「分割」、「切断」を意味するギリシャ文字の「τ」（タウ）や、パルテノン
神殿に黄金分割を用いたギリシャの彫刻家フィディアスの頭文字をとって、「φ」（ファイ）など
が用いられる。２０世紀の初め、アメリカのマーク・バンが黄金比にφという名を付けたとも言
われる。

　ものの本によると、「手首は手の先から肘までを黄金比で分割」していると言われる。

　実際に、自分の腕で概算で測ってみると、　手の先〜手首が２０cm、手首〜肘が３０cmで、
その比は、　３０/２０＝１．５　くらいになる。

　この比がぴったりと黄金比になる方は、いらっしゃるのだろうか？

　人の肘から中指の先端までの長さを基にした単位に１キュビット（ｃｕｂｉｔ）がある。その名称
は、ラテン語で肘を意味するｃｕｂｉｔｕｍに由来する。年齢によっても違うが、約４３〜５３ｃｍく
らいまでの長さのことをいう。イスタンブール考古学博物館には、１キュビット（５１７ｍｍ）の青
銅製標準原器があるそうだ。


　黄金比が出現する一番有名な図形は、正五角形であろう。

　


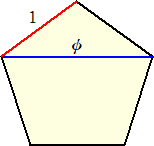
　下図は正５角形の一部分であるが、黄金三角形と言われる。

　

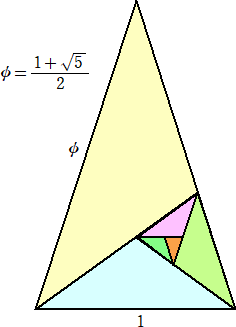
　正五角形の一辺の長さに対する対角線の長さなど、至る所に黄金比が隠れている。それ
が正五角形に対してある種の畏敬の念を抱く所以であろうか？


　ｍ/ｎ＝（１＋）/２　であるとき、縦の長さｎ、横の長さｍの長方形は黄金長方形と言わ
れる。
　


　黄金長方形は、次のように作図される。

　１辺の長さがｎの正方形を作図し、底辺の中点と頂点を結ぶ長さを半径とし、底辺の中点
を中心とする円弧を描けば、下図のような黄金長方形が得られる。

　


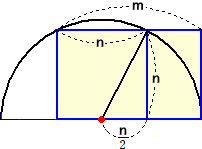
　普段使っている名刺（５５×９１ｍｍ・・・４号サイズ）は、ｍ/ｎがおおよそ１．６５位、手帳は、
Ｂ７版（９１×１２８ｍｍ）というコンパクトサイズのものを使っているが、そのｍ/ｎがおおよそ
１．４１位等、黄金長方形そのものではないが、それに近いものが日常生活で多く見受けら
れる。国旗の縦・横の比も国によって様々であるが、２：１＋ の黄金比（１．６１８）に近い
ものが多い。

　最も多いのが、２：３ で、日本・スペイン・インドなど、次が、１：２ のイギリス・オーストラリア・
カナダなど、３番目に多いのが、３：５ のドイツ・ルクセンブルク・パラグアイなど。

　最も横長の国はカタールで１１：２８となっている。１：１の正方形の国旗を持つ国は２つあり
スイスとバチカンである。これなんかはクイズ番組に出そうな雰囲気である。


　黄金長方形から下図のように、正方形を切り出せば、順次、黄金長方形が得られる。

　　

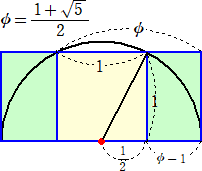
　１：φが黄金比のとき、φ−１：１も黄金比となる。

　実際に、φ＝（１＋）/２　なので、

　φ−１＝（−１）/２　から、１/（φ−１）＝２/（−１）＝（１＋）/２　だからである。


（追記）　令和３年１１月１１日付け

　上記の計算から、φ＝（１＋）/２　のとき、　１/（φ−１）＝φ　すなわち、φ²−φ＝１
が成り立つ。

　これを、　φ²＝φ＋１　から、　φ＝√（φ＋１）　と変形すると、再帰的な式が出来る。

　この式を利用すると、電卓を用いて、黄金比が体験できる。

（手順）　１．φ＝１とおく。（実際は、φは任意の数値でよい）

　２．φに１を足して、その平方根をとる。

　３．２．で得られた数値をφとして、２．の操作を繰り返す。

　４．φの数値に変化がなくなったら、その数値が黄金比となる。


　実際に、電卓で上記の手順を実行してみよう。

　電卓の画面（手元にある１０桁の電卓を利用）

　１　（１を入力　：　「１」「＝」）
　２　（１を足す　：　「＋」「１」「＝」）
　１．４１４２１３５６２　（平方根をとる　：　「√」）
　２．４１４２１３５６２　（１を足す　：　「＋」「１」「＝」）
　１．５５３７７３９７３　（平方根をとる　：　「√」）
　２．５５３７７３９７３　（１を足す　：　「＋」「１」「＝」）
　１．５９８０５３１８２　（平方根をとる　：　「√」）
　２．５９８０５３１８２　（１を足す　：　「＋」「１」「＝」）
　１．６１１８４７７５３　（平方根をとる　：　「√」）
　２．６１１８４７７５３　（１を足す　：　「＋」「１」「＝」）
　１．６１６１２１２０６　（平方根をとる　：　「√」）
　２．６１６１２１２０６　（１を足す　：　「＋」「１」「＝」）
　１．６１７４４２７９８　（平方根をとる　：　「√」）
　２．６１７４４２７９８　（１を足す　：　「＋」「１」「＝」）
　１．６１７８５１２９　　（平方根をとる　：　「√」）
　２．６１７８５１２９　　（１を足す　：　「＋」「１」「＝」）
　１．６１７９７７５３　　（平方根をとる　：　「√」）
　２．６１７９７７５３　　（１を足す　：　「＋」「１」「＝」）
　１．６１８０１６５４１　（平方根をとる　：　「√」）
　２．６１８０１６５４１　（１を足す　：　「＋」「１」「＝」）
　１．６１８０２８５９７　（平方根をとる　：　「√」）
　２．６１８０２８５９７　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３２３２２　（平方根をとる　：　「√」）
　２．６１８０３２３２２　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３４７３　（平方根をとる　：　「√」）
　２．６１８０３３４７３　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３８２９　（平方根をとる　：　「√」）
　２．６１８０３３８２９　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９３９　（平方根をとる　：　「√」）
　２．６１８０３３９３９　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９７３　（平方根をとる　：　「√」）
　２．６１８０３３９７３　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９８３　（平方根をとる　：　「√」）
　２．６１８０３３９８３　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９８６　（平方根をとる　：　「√」）
　２．６１８０３３９８６　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９８７　（平方根をとる　：　「√」）
　２．６１８０３３９８７　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９８８　（平方根をとる　：　「√」）
　２．６１８０３３９８８　（１を足す　：　「＋」「１」「＝」）
　１．６１８０３３９８８　（平方根をとる　：　「√」）

　以上から、φの値は、　１．６１８０３３９８８　に近づいたことが分かる。

　「＋」「１」「＝」「√」を１セットとすると、ちょうど２０セットで計算出来たことになる。


　　最近、次のような図形に対しても、黄金比が現れることを知った。

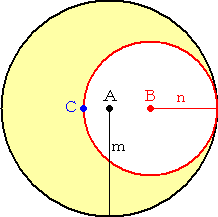左図では、半径 ｍ の円Ａの周上で、半径 ｎ の円Ｂ 　　が接している。 　　　円Ａから円Ｂを取り除いた図形は月形になっている。 　　　この月形の図形の重心Ｃが、円Ｂの周上にあるもの 　　とする。 　　　このとき、　比 ｍ/ｎ の値は、黄金比になる。 　　　実際に、確かめてみよう。

　図形の上下対称性から、月形の図形の重心Ｃは直線ＡＢ上にある。

点Ａを支点として２つの図形Ｂ、Ｃはつりあっているので、

　π（ｍ²−ｎ²）×（２ｎ−ｍ）＝πｎ²×（ｍ−ｎ）

これより、　　　ｍ³−２ｍ²ｎ＋ｎ³＝０　　　なので、　　（ｍ−ｎ）（ｍ²−ｍｎ−ｎ²）＝０

ｍ≠ｎ　としてよいので、　　　ｍ²−ｍｎ−ｎ²＝０

　よって、比 ｍ/ｎ の値は、

　　

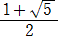
　このことは、比 ２ｍ/２ｎ を考えることにより、点Ｃは円Ａの直径を黄金分割していることも
示している。

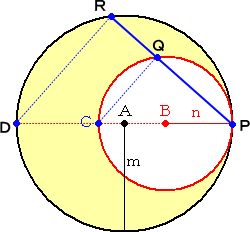さらに、左図のように円Ａと円Ｂの接点Ｐを通る 　　弦が２円Ａ、Ｂと交わる点をそれぞれＲ、Ｑとする 　　と、 　　　　　　Ｑは弦ＰＲを黄金分割している 　　ことも分かる。 　　　証明は明らかであろう。 　　（左図において、△ＰＱＣ∽△ＰＲＤに注意）

　また、次のような図形に対しても黄金比が現れることに驚いてしまう。

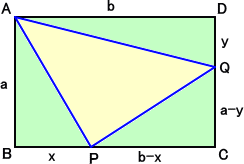左図のような長方形ＡＢＣＤにおいて、２点Ｐ、Ｑ 　　をそれぞれ辺ＢＣ、ＣＤ上にとる。 　　　このとき、３つの三角形 　　　　　　△ＡＢＰ　、　△ＰＣＱ　、　△ＱＤＡ 　　の面積が等しい場合を考える。

　条件より、　ａｘ/２ ＝ (ｂ−ｘ)(ａ−ｙ)/２ ＝ ｂｙ/２ 　即ち、　ａｘ ＝ (ｂ−ｘ)(ａ−ｙ) ＝ ｂｙ　が成
り立つので、　ｙ ＝ (ａ/ｂ)ｘ　を　ａｘ ＝ (ｂ−ｘ)(ａ−ｙ)　に代入して整理すると、

　（ｂ−ｘ）² ＝ ｂｘ　すなわち、　（ｂ−ｘ）²−ｘ（ｂ−ｘ）−ｘ² ＝ ０

このことから、　（ｂ−ｘ）/ｘ　の値は、

　　

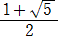
　同様にして、　（ａ−ｙ）/ｙ　の値は、　（ａ−ｙ）²−ｙ（ａ−ｙ）−ｙ² ＝ ０　より、

　

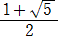
　したがって、３つの三角形の面積が等しいとき、２点Ｐ、Ｑは、それぞれ辺ＢＣ、ＣＤを黄金
分割していることが分かる。


（参考文献：アルプレヒト・ボイテルスパッヒャー、ベルンハルト・ペトリ　著
　　　　　　　 柳井　浩　訳　　　黄金分割　　　（共立出版））


（追記）　平成２６年７月２８日付け

　これこれこういう条件だと黄金分割になるということは上記で示されたが、実際に与えられ
た線分を黄金分割するという問いに対しては無力である。

　ユークリッド原論第２巻１１によれば、次のような作図法が知られている。

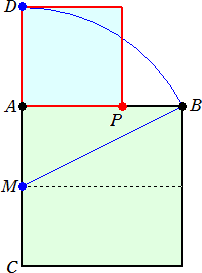与えられた線分ＡＢを１辺とする正方形を作図し、辺ＡＣ 　の中点をＭとする。 　　辺ＣＡの延長上にＢＭ＝ＭＤとなる点Ｄをとる。 　　ＡＤを１辺とする正方形を作図すると、点Ｐが、線分ＡＢ 　を黄金分割する点となる。 （作図の基本的な考え方は正５角形の作図と同様である。）

　実際に、ＡＢ＝２ａ　とおくと、ＢＭ＝ＭＤ＝ａ　で、ＡＤ＝ＡＰ＝（−１）ａ

　したがって、ＢＰ＝（３−）ａ　なので、ＡＰ/ＢＰ＝（−１）/（３−）＝（１＋）/２


（追記）　当ＨＰ読者のＨＮ「Ｈ．Ｎ．」さんから、黄金分割に関する話題をメールで頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２７年５月４日付け）

　図書館で見つけた本からの課題ですが、お知恵を拝借できませんでしょうか？

問題７５　内接円の半径が１の二等辺三角形で、等辺の長さが最小のものを考える。
　　　　三角形の高さはどのくらいか？
（「黄金分割」　H.ヴァルサー著　蟹江幸博訳　日本評論社2002年刊　より）

　著者は、τ²　（ただし、τ＝（１＋）/２　：黄金比）という解答しか記していません。訳者
は、等辺をa、三角形の高さをhとして、a²=h(h-1)²/(h-2) を導き、それを微分することによっ
て解が示せるとしつつ、微分を 使わない解法を募集しておられます。著書の流れからして微
分を要求するようなところではないように私も感じます。

　貴サイトを通じて、ひろく意見を募っていただけましたら幸いです。


（コメント）　等辺の長さが最小のとき、高さが（黄金比）²になるという事実に興味を持ったの
　　　　　　で計算してみた。

　等辺をa、三角形の高さをh、底辺を２ｘとすると、三平方の定理から、　ａ²＝ｘ²＋ｈ²

　また、三角形の面積の計算から、　２ｘ・ｈ/２＝（ａ＋ａ＋２ｘ）・１/２　より、　ｘｈ＝ａ＋ｘ

これより、　ｘ＝ａ/（ｈ−１）　なので、　ａ²＝｛ａ/（ｈ−１）｝²＋ｈ²

　すなわち、　ａ²｛１−１/（ｈ−１）²｝＝ｈ²　より、　ａ²＝ｈ（ｈ−１）²/（ｈ−２）

　ｙ＝ｈ（ｈ−１）²/（ｈ−２）　とおく。題意より、　ｈ＞２　としてよい。

　ｈに関して微分すると、　ｙ’＝２（ｈ−１）（ｈ²−３ｈ＋１）/（ｈ−２）²

　増減表により、　ｈ＝（３＋）/２　のとき、ｙ は極小かつ最小である。

　τ²＝｛（１＋）/２｝²＝（３＋）/２　なので、以上から、等辺の長さが最小となる高さ

は、τ²　である。


　さて、微分を用いて結果は示されたものの、このことを微分を使わないで示そうとする場合
どのように考えればいいのだろうか？


（追記）　令和３年６月１０日付け

　黄金比はφで表すことが多い。φは次の性質を持つ。

　φ²−φ−１＝０　すなわち、　φ＝（１＋）/２＝１．６１８・・・　で、

　１/φ＝（−１）/２＝０．６１８・・・

また、　φ²−φ−１＝０　から、　φ²＝１＋φ　が成り立ち、

　φ/（１＋φ）＝１/φ　や　φ−１＝１/φ　、φ＝１＋１/φ

また、　φ＝（１＋φ）/φ＝１/｛φ/（１＋φ）｝＝１/｛１−１/（１＋φ）｝

　φ＝√（１＋φ）　より、　φ＝√｛１＋√（１＋φ）｝

などとも書き直せる。

　上記の関係を図にまとめておこう。




　このようなφの表現を駆使する問題を考えてみよう。


問題　　平行四辺形ＡＢＣＤにおいて、辺ＡＤの黄金分割点をＥとおく。即ち、ＡＥ＝φＥＤ　で
　　　　ある。直線ＢＥと直線ＣＤの交点をＦとおく。このとき、　△ＡＢＥ＝△ＥＣＦ　が成り立つ
　　　　ことを示せ。
　

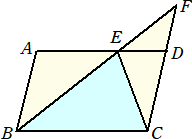
（解）　ＡＢ＝ａ、ＡＤ＝ｂ、∠ＢＡＤ＝θとおく。

　題意より、　ＡＥ＝φ（ｂ−ＡＥ）　なので、　ＡＥ＝（φ/（１＋φ））ｂ＝ｂ/φ

　よって、　△ＡＢＥ＝（ａｂｓｉｎθ/２）・（１/φ）　である。

　ここで、△ＡＢＥ∽△ＤＦＥ　より、ＡＢ：ＡＥ＝ＤＦ：ＤＥ　なので、

　ａ ： ｂ/φ＝ＤＦ ： （１−１/φ）ｂ　すなわち、　ＤＦ＝（φ−１）ａ＝ａ/φ

　このとき、△ＥＣＦ＝△ＥＤＦ＋△ＥＣＤ　において、

△ＥＤＦ＝（１/２）・（１−１/φ）ｂ・ａ/φ・ｓｉｎθ＝（ａｂｓｉｎθ/２）・（φ−１）/φ²

△ＥＣＤ＝（ＥＤ/ＡＥ）△ＡＢＥ＝（１/φ）△ＡＢＥ＝（ａｂｓｉｎθ/２）・（１/φ²）　より、

　△ＥＣＦ＝（ａｂｓｉｎθ/２）・（（φ−１）/φ²＋１/φ²）＝（ａｂｓｉｎθ/２）・（１/φ）

　以上から、　△ＡＢＥ＝△ＥＣＦ　が成り立つ。　　（終）


　次のような等式も興味深い。

　θ＝１８°のとき、

　ｓｉｎθ＝（φ−１）/２　、ｃｏｓθ＝√（２＋φ）・（１/２）

　ｔａｎθ＝（φ−１）/√（２＋φ）


　θ＝３６°のとき、

　ｓｉｎθ＝√（３−φ）・（１/２）　、ｃｏｓθ＝φ/２

　ｔａｎθ＝｛√（３−φ）｝/φ


　実際に、θ＝１８°のとき、　５θ＝９０°　すなわち、　３θ＝９０°−２θ　より、

　ｓｉｎ３θ＝ｃｏｓ２θ　なので、　３ｓｉｎθ−４ｓｉｎ³θ＝１−２ｓｉｎ²θ

　整理して、　４ｓｉｎ³θ−２ｓｉｎ²θ−３ｓｉｎθ＋１＝０　から、

　　（ｓｉｎθ−１）（４ｓｉｎ²θ＋２ｓｉｎθ−１）＝０

　ｓｉｎθ≠１　なので、　４ｓｉｎ²θ＋２ｓｉｎθ−１

　これを解いて、　ｓｉｎθ＝（−１±）/４

　ｓｉｎθ＞０　なので、　ｓｉｎθ＝（−１＋）/４＝（φ−１）/２

　ｃｏｓ²θ＝１−ｓｉｎ²θ＝１−（−１＋）²/１６＝（５＋）/８＝（２＋φ）/４

　ｃｏｓθ＞０　なので、　ｃｏｓθ＝√（２＋φ）・（１/２）

　よって、　ｔａｎθ＝ｓｉｎθ/ｃｏｓθ＝（φ−１）/√（２＋φ）

　θ＝３６°のとき、

　ｓｉｎθ＝２ｓｉｎ１８°ｃｏｓ１８°＝（φ−１）√（２＋φ）・（１/２）

ここで、　（φ−１）²（２＋φ）＝（２−φ）（２＋φ）＝４−φ²＝３−φ　なので、

　ｓｉｎθ＝√（３−φ）・（１/２）

　ｃｏｓθ＝ｃｏｓ²１８°−ｓｉｎ²１８°
　　　　　＝（５＋）/８−（−１＋）²/１６＝（１＋）/４＝φ/２

　よって、　ｔａｎθ＝｛√（３−φ）｝/φ


　黄金分割点から順次新しい黄金分割点を与える線分の作図を考えてみよう。

　線分ＡＢに対して、点Ｃは黄金分割点である。ＡＢのＡの延長上に点Ｄをとり、ＡがＤＣの黄
金分割点になるようにせよ。



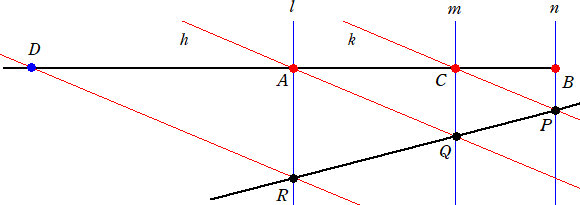
　３点 Ａ、Ｃ、Ｂ を通る平行線をそれぞれ ｌ、ｍ、ｎ とする。２点 Ｃ、Ａ を通り、ｍ、ｌ と異なる
平行線をそれぞれ ｋ、ｈ とし、平行線 ｎ。ｍ との交点をそれぞれ Ｐ、Ｑ とおく。

　直線ＰＱと直線 ｌ との交点をＲとおき、点Ｒを通り、ｈ と平行に直線を引き、直線ＡＢとの交
点をＤとおく。

　この点Ｄが求める点である。

　実際に、題意より、ＡＣ＝φ・ＣＢ　（ただし、φは、黄金比）　なので、平行線の公理から、

　ＲＱ＝φ・ＱＰ　が成り立ち、さらに、　ＤＡ＝φ・ＡＣ

　よって、　点Ａは線分ＤＣの黄金分割点である。


（追記）　令和３年７月１８日付け

　次のような場面でも黄金比が出現する。

　直角三角形の３つの角が等比数列となるとき、公比はいくらか？

（解）　公比を ｒ とおくと、３つの角は、θ、ｒθ、ｒ²θ　とおける。

　３つの場合が考えられる。

（１）　ｒ²θ＝９０°のとき、　θ＋ｒθ＝ｒ²θ　が成り立つ。

　すなわち、　ｒ²−ｒ−１＝０　で、ｒ＝（１＋）/２（＝φ）は黄金比となる。

　もちろん、２次方程式の解としては、　ｒ＝（１−）/２　も考えられるが、この場合は、

　ｒ＝−１/φ＜０　で、不適となる。

（２）　ｒθ＝９０°のとき、　θ＋ｒ²θ＝ｒθ　が成り立つ。

　すなわち、　ｒ²−ｒ＋１＝０　であるが、この方程式を満たす実数解は存在しない。

　よって、ｒθ＝９０°は起こりえない。

（３）　θ＝９０°のとき、　ｒθ＋ｒ²θ＝θ　が成り立つ。

　すなわち、　ｒ²＋ｒ−１＝０　で、ｒ＝１/φ、−φ　となるが、ｒ＝−φ　は不適で、

　ｒ＝１/φ　のみが解となる。やはり、黄金比で表される。


（コメント）　具体的に、角度を近似的に求めると、直角三角形の３つの角は、

　３４．３８°、５５．６２°、９０°となるようだ。

　同様の問題で、直角三角形の３つの角が等差数列となるときの公差は一意に定まらない。

ただし、等差中項は６０°で一意的である。


（追記）　令和３年７月２１日付け

　丸いケーキがあり、これを５等分する場合、まず思いつくのは正５角形による５等分だろう。

　　

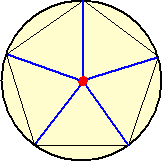
　これに対して、黄金分割を用いる方法もある。

　ケーキの中心をＯとし、ＯＡは半径である。ＯＡ＝２ＯＢとなるＢをとり、直角三角形ＯＡＢを
考える。斜辺ＡＢにＯより垂線の足Ｈを下ろす。

　このとき、Ｏを中心として半径ＯＨの円を描くと、Ｃは線分ＡＤの黄金分割点、Ｄは線分ＣＥ
の黄金分割点となる。



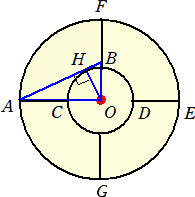
　実際に、ＯＢ＝１とすると、ＯＡ＝２で、ＡＢ＝　であるので、ＯＨ×/２＝２×１/２＝１

から、　ＯＨ＝２/　

このとき、　ＣＤ＝４/　、　ＡＣ＝２−２/＝２（−１）/　なので、

　ＣＤ/ＡＣ＝４/÷２（−１）/＝２/（−１）＝（１＋）/２＝φ（黄金比）

　よって、ＣはＡＤの黄金分割点である。

　同様にして、Ｄは線分ＣＥの黄金分割点となる。

ここで、ＯＣ＝２/を半径とする円の面積は、（４/５）πで、これは丁度、ＯＡ＝２を半径と

する円の面積４πの１/５である。上図のように、ＯＡを半径とする円とＯＣを半径とする円の

間に挟まれた部分を４等分すれば、黄金分割による丸いケーキの５等分が可能である。


（追記）　令和４年１月９日付け

　次のような幾何学的な黄金分割点の作図法が知られている。

　

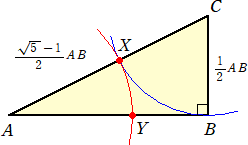
　このとき、Ｙは、線分ＡＢの黄金分割点となる。



　　　　以下、工事中