線形結合の問題 
3円と5円の2種類の切手のみで、8円以上のすべての郵便料金を払うことができるだろ
うか?
(答) 払える!
この問題は、平成21年3月21日付けで、当HPがいつもお世話になっているS(H)さ
んにご紹介いただいたもの。素朴な問題に引かれました!
数学的には、「8以上の自然数は、3と5の線形結合で表されるか」という問題である。
証明は、易しい。 自然数 N に対して、
N=8 ならば、 N=3・1+5・1=8 で、 8は、3と5で表すことが出来る。
そこで、N≧9 とする。Nを3で割った商を Q とし、余りを R とおくと、
N=3・Q+R (ただし、R=0、1、2)
と書ける。N≧9 なので、 Q≧3 である。
このとき、
R=0 ならば、 N=3・Q で、Nは3のみで表される。
R=1 ならば、 3・(−3)+5・2=1 なので、
N=3・Q+1=3・Q+3・(−3)+5・2=3・(Q−3)+5・2
Q−3≧0 に注意して、 Nは、3と5で表すことが出来る。
R=2 ならば、 N=3・Q+2=3・Q+3・(−1)+5・1=3・(Q−1)+5・1
Q−1>0 に注意して、 Nは、3と5で表すことが出来る。
以上から、8以上のすべての自然数は、3と5の線形結合で表される。
平成21年3月28日付けで、HN「あとねこ」さんより、次のように考えると視覚的に(?)分
かるかもという解答をお寄せいただいた。あとねこさんに感謝します。
| 8 |
9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
| 23 |
24 |
25 |
26 |
27 |
| ・・・・・ |
・・・・・ |
・・・・・ |
・・・・・ |
・・・・・ |
8=3+5 、 9=3・3 、 10=5・2 、 11=3・2+5 、 12=3・4
と、第1行の数はすべて、3と5の線形結合で表される。
第2行以下の数については、第1行の数に5の倍数を加えることにより得られる。
したがって、8以上のすべての自然数は、3と5の線形結合で表される。
(コメント) 私の解答に比べて、視覚的に説得力がありますね!
この考え方は、成海璃子主演のTVドラマ「受験の神様」でも紹介された。
この話題に関連して、平成21年3月29日付けで、S(H)さんは、
3円、5円、80円の3種類の切手のみで、2000円の郵便料金を支払う方法は何通りあ
るか?
という問題を考えられた。この問題は、
等式 3x+5y+80z=2000 を満たす 0 以上の整数 x 、y 、z
の組( x ,y ,z )は何
組あるか?
ということに等しい。
80z≦2000 より、 z≦25 なので、 z=0、1、2、・・・、24、25 について調べれば
よい。
z=25 のとき、 3x+5y=0 より、 x=0 、y=0
z=24 のとき、 3x+5y=80 で、 5y≦80 より、 y≦16
このとき、( x ,y )=( 0 ,16 )、( 5 ,13 )、( 10
,10 )、
( 15
,7 )、( 20 ,4 )、( 25 ,1 )
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
等々、場合の数はたくさんありそうですね!
さらに、S(H)さんは、次の問題も紹介された。
1. 50円切手と80円切手がそれぞれたくさん(無数に)ある。これらを使って支払うことが
出来ない郵便料金は何通りあるか?ただし、郵便料金は、10の倍数とする。
(解) 10円(×)、20円(×)、30円(×)、40円(×)、50円(○)、60円(×)、70円(×)、
80円(○)、90円(×)、100円=50円*2(○)、110円(×)、120円(×)、
130円=50円+80円(○)、140円(×)、150円=50円*3(○)、
160円=80円*2(○)、170円(×)、180円=50円*2+80円(○)、190円(×)、
200円=50円*4(○)、210円=50円+80円*2(○)、220円(×)、
230円=50円*3+80円(○)、240円=80円*3(○)、250円=50円*5(○)、
260円=50円*2+80円*2(○)、270円(×)、280円=50円*4+80円(○)、
290円=50円+80円*3(○)、300円=50円*6(○)、
310円=50円*3+80円*2(○)、320円=80円*4(○)、・・・・・
以下、280円、290円、300円、310円、320円 の支払いパターンに、50円切手を何
枚かずつ追加することにより、280円以上のすべての金額が50円と80円の組合せにより
得られる。
したがって、求める場合の数は、
10円、20円、30円、40円、60円、70円、90円、110円、120円、140円、170円、
190円、220円、270円
の14通りである。 (終)
2. 13円、14円、15円、16円、17円の3種類の切手のみで、すべての金額が支払える
のは何円以上の場合か?
(追記) 平成22年6月5日付け
上記では、
3円、5円の2種類の切手のみで、8円以上の全ての郵便料金が払えること
5円、8円の2種類の切手のみで、28円以上の全ての郵便料金が払えること
が示された。
この話題に関連して、当HPがいつもお世話になっているFNさんが、問題の一般化を試み
られた。(平成22年6月2日付け)
a 、 b を互いに素な自然数とする。すべての整数が整数 x 、 y を使って、
ax+by の形
で表されることはよく知られている。ここで、 x 、 y を0以上としたとき、
ax+by の形で表
される整数はどのような数であろうか。ある数以上はこの形で表すことができる。そのある
数を求めてください。
すなわち、
a 、 b を互いに素な自然数とする。次の命題が成り立つ最小の自然数Nを求めよ。
「N以上の整数は0以上の整数 x 、 y を使って ax+by の形で表すことができる。」
同じことであるが次の形に書いてもいいだろう。
a 、 b を互いに素な自然数とする。0以上の整数 x 、 y を使って ax+by の形で
表すことができない最大の整数を求めよ。
FNさんが、a=5、b=7 の場合の解答を寄せられた。(平成22年6月4日付け)
0以上の整数 x 、 y を使って、5x+7y の形で表される数の集合をAとする。
1から順に自然数を5個毎に行を変えながら書いていく。(Aに入らないものは黒字)
| 1 |
2 |
3 |
4 |
5 |
| 6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
| 26 |
27 |
28 |
29 |
30 |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
5本の列は、5で割った余りが、1、2、3、4、0 であ
る自然数を小さいものから順に並べたものである。
右端の列、即ち、5で割り切れる数はすべてAに入っ
ている。それ以外の列は、どこかで7の倍数が現れ、
それ以後はすべてAに入る。
右端以外の各列で最初に現れる7の倍数のうち最も
遅く現れるのは、28である。
従って、Aに入っていない最大の数は、28の現れる列で、28の上にある23である。
即ち、24以上の整数はすべてAに属する。
これと同じことを、一般の場合もやればいいのだが、具体的な場合と違い意外と書きにく
い。
GAI さんが、
a 、 b を互いに素な自然数とする。0以上の整数 x 、 y を使って ax+by の形で
表すことができない最大の整数を求めよ。
という問題について、次のような表を作られた。(平成22年6月6日付け)
| a |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| b |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
4 |
5 |
7 |
8 |
10 |
11 |
13 |
14 |
16 |
17 |
19 |
| 最大の整数 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
25 |
29 |
31 |
35 |
| a |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
| b |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
6 |
7 |
8 |
9 |
11 |
12 |
13 |
14 |
16 |
17 |
| 最大の整数 |
11 |
17 |
23 |
29 |
35 |
41 |
47 |
53 |
19 |
23 |
27 |
31 |
39 |
43 |
47 |
51 |
59 |
63 |
| a |
5 |
5 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
| b |
18 |
19 |
7 |
11 |
13 |
17 |
19 |
8 |
9 |
10 |
11 |
12 |
13 |
15 |
16 |
17 |
18 |
| 最大の整数 |
67 |
71 |
29 |
49 |
59 |
79 |
89 |
41 |
47 |
53 |
59 |
65 |
71 |
83 |
89 |
95 |
101 |
| a |
7 |
8 |
8 |
8 |
8 |
8 |
8 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
| b |
19 |
9 |
11 |
13 |
15 |
17 |
19 |
10 |
11 |
13 |
14 |
16 |
17 |
19 |
| 最大の整数 |
107 |
55 |
69 |
83 |
97 |
111 |
125 |
71 |
79 |
87 |
95 |
119 |
127 |
143 |
さらに、FNさんは、
a 、 b を互いに素な自然数とする。0以上の整数 x 、 y を使って ax+by の形で
表すことができない最大の自然数は、 ab−a−b である
ことを次のように証明された。(平成22年6月7日付け)
(証明) ab−a−b が、ax+by ( x 、y は0以上の整数)の形には書けないことを、まず
示す。
ab−a−b=ax+by ( x 、y は0以上の整数)の形に書けるとする。
a(b−1−x)=b(y+1) で、a 、b は互いに素より、y+1
は a の倍数となる。
y+1≧1 より、 y+1≧a なので、 b(y+1)≧ab
一方、 a(b−1−x)<ab なので、これは矛盾である。
よって、ab−a−b は、ax+by ( x 、y は0以上の整数)の形には書けない。
次に、ab−a−b+1 以上の整数はすべて、ax+by ( x 、y
は0以上の整数)の形に
書けることを示す。
整数 n が、 n≧ab−a−b+1=(a−1)(b−1) を満たすとする。
n 、 n−b 、 n−2b 、 ・・・ 、 n−(a−1)b を a
で割った余りを考える。
これらは、a 個あるので、次の(1)(2)のどちらかが成り立つ。
(1) これらの中に同じものがある。
(2) これらの中に0がある。
(1)のとき、異なる s、t (0≦s<t≦a−1)が存在して、n−sb−(n−tb)=(t−s)b が
a で割り切れる。b と a は互いに素であるから、t−s が a で割り切れる。
しかるに、0<t−s≦a−1 より、それは不可能である。
(2)のとき、n−sb を a で割った余りが 0 であるとする。このとき、n−sb=ta と書ける。
n=sb+ta において、s≧0 、t≧0 である。
実際に、n−sb≧n−(a−1)b≧ab−a−b+1−ab+b=−a+1 より、n−sb+a≧1
で、n−sb=ta から、 (t+1)a≧1 より、 t+1≧1 なので、 t≧0 と言える。
以上から、求める最大の自然数が、ab−a−b であることが示された。 (終)
(コメント) FNさんによれば、「ab−a−b」が自然に出る構成的・発見的な証明ではないで
すが...とのことですが、数学らしい立派な証明ですね!
また、上記の問題と同趣旨の問題が、昭和62年度 防衛大学校の記述式問題として出題
されている。世間的には、難問と認識されているようである。
a、b を負でない整数とし、3a+7b の形で表せる自然数全体を S とする。たとえば、
47=3×4+7×5 ゆえ 47はSの要素である。このとき、次の問に答えよ。
(1) 10以下の自然数でSの要素であるものをすべて求めよ。
(2) n がSの要素であるとき、n+3 もSの要素であることを示せ。
(3) 連続する3個の自然数 m 、m+1 、m+2 がいずれもSの要素となるような自然
数 m のうち最小のものを求めよ。
(4) (3)で求めた m 以上の任意の自然数 n は、Sの要素であることを証明せよ。
(解)(1) 1≦3a+7b≦10 において、a≧0、b≧0 に注意して、
( a , b )=( 0 , 1 )、( 1 , 0 )、( 1 ,
1 )、( 2 , 0 )、( 3 , 0 )
が条件を満たす。よって、求める要素は、 3、6、7、9、10
(2) 題意より、 負でない整数 a、b を用いて、 n=3a+7b と書ける。
このとき、 n+3=3(a+1)+7b において、a+1、b は負でない整数なので、
n+3 は、S の要素である。
(3) 11は、S の要素でない。実際に、11が、S の要素であると仮定すると、負でない整
数 a、b を用いて、 11=3a+7b と書ける。
ここで、a=0 とすると、11が7で割り切れることになるので、a≧1
このとき、 8=3(a−1)+7b において、a−1、b は負でない整数なので、8 は、S
の要素となる。しかるに、これは(1)の結果に矛盾する。
よって、11は、S の要素でない。
(1)より、9、10 はSの要素なので、(2)より、12、13もSの要素である。
また、14=3・0+7・2 と書けるので、14もSの要素である。
以上から、連続する3個の自然数 m 、m+1 、m+2 がいずれもSの要素となる
ような自然数 m のうち最小のものは、12である。
(4) (3)の結果より、12、13、14 は、Sの要素である。12以上の任意の自然数
n を3
で割った余りで分類する。
n=3・p+12 (pは負でない整数) のとき、(2)の結果と、12がSの要素である
ことから、n はSの要素であることが分かる。
n=3・p+13 (pは負でない整数) のとき、(2)の結果と、13がSの要素である
ことから、n はSの要素であることが分かる。
n=3・p+14 (pは負でない整数) のとき、(2)の結果と、14がSの要素である
ことから、n はSの要素であることが分かる。
以上から、12以上の任意の自然数 n に対して、Sの要素であることが示された。(終)
(コメント) (4)の証明は厳密には数学的帰納法で示す必要があるかもしれない。
あとねこさんがFNさんの証明の別証を考えられた。(平成22年11月9日付け)
a、b
を互いに素な自然数とする。0以上の整数 x、y を使って ax+byの形で表す
ことができない最大の自然数は ab−a−b である。
(証明) b>a
として考える。0以上の整数 x、y を使って、ax+by の形で表される数の集合
をAとする。1から順に b 個毎に行を変えながら ab
まで書く。
1 2 3 … b
b+1 … … … 2b
・ ・
・ ・
・ ・
(a-1)b+1 … … …
ab
a の倍数に着目したとき、a の倍数は各列1つしか現れない。
実際に、 tb≡f (mod a) のとき、t(a+n)b≡f (mod a) が成り立つ n は
(
t と n は整数)
t(a+n)b≡(a+n)f≡nf (mod a)
であるから、n=ka+1
(kは整数)である。
すなわち、 b、2b、3b、・・・ab は a で割った余りがそれぞれ違うことを意味する。
ここで、ある列に a の倍数が2つあるとすると、ib と jb を a で割った余りが一致するとい
うことになる。( i 、 j は自然数で、 i≠j 、 i≦a 、 j≦a)
しかるに、これは矛盾。同列に、 a の倍数が3つ以上であっても同様に矛盾する。
したがって、 a
の倍数は各列1つしか現れない。
右端の列、即ち、b で割り切れる数はすべてAに入っている。それ以外の列は、どこかで
a の倍数が現れ、それ以後はすべてAに入る。
a の倍数は各列1つしか現れないので、最後にAに含まれる列は、a(b−1)
が含まれる列
なので、表すことの出来ない最大の数は、その1行前の数字 a(b−1)−b=ab−a−b と
なる。(証終)
(コメント) あとねこさん、別証ありがとうございます。あとねこさんの証明を参考にして私流
に書き直してみました。
(証明) b>a として考える。0以上の整数 x、y を使って、ax+by の形で表される数の集合
をAとする。1から順に b
個毎に行を変えながら ab まで書く。
1 2 3 … b
b+1 … …
… 2b
・ ・
・ ・
・ ・
(a-1)b+1 … … …
ab
a の倍数に着目したとき、a
の倍数は各列1つしか現れない。
実際に、任意の列 k、b+k、2b+k、・・・、(a−1)b+k (kは自然数で、1≦k≦b)に
おいて、ある自然数 m、n (1≦m<n≦a)が存在して、 mb+k≡nb+k (mod a) が
成り立つと仮定すると、
(m−n)b≡0 (mod a) で、(a,b)=1 より、 m−n≡0 (mod a) となる。
しかるに、これは、 1≦m<n≦a に矛盾する。
したがって、a個の任意の列 k、b+k、2b+k、・・・、(a−1)b+k の各項を
a で割った
余りは全て異なる。このとき、この列の項で、a で割り切れるものがただ一つ存在する。
右端の列、即ち、b で割り切れる数はすべてAに入っている。それ以外の列は、どこかで
a の倍数が現れ、それ以後はすべてAに入る。
a の倍数は各列1つしか現れないので、最後にAに含まれる列は、a(b−1)
が含まれる列
なので、表すことの出来ない最大の数は、その1行前の数字 a(b−1)−b=ab−a−b と
なる。(証終)
当HPがいつもお世話になっているHN「FN」さんが、この話題に関連して、次の問題を提
起された。(平成22年11月10日付け)
a、b を互いに素な自然数とする。0以上の整数 x、y を使って ax+byの形で表す
ことができない自然数の個数を求めよ。
この問題は、上記のS(H)さんの問題の一般化である。
S(H)さんの問題を単純化して、
5円切手と8円切手がそれぞれたくさん(無数に)ある。これらを使って支払うことが
出来ない郵便料金は何通りあるか?
この問題を、あとねこさんやFNさんの解答に照らして考えると次のように解けるだろう。
0以上の整数 x 、 y を使って、5x+8y の形で表される数の集合をAとする。
1から順に自然数を5個毎に行を変えながら書いていく。(Aに入らないものは黒字)
5本の列は、5で割った余りが、1、2、3、4、0 である自然数を小さいものから順に並べ
たものである。
| 1 |
2 |
3 |
4 |
5 |
| 6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
| 26 |
27 |
28 |
29 |
30 |
| 31 |
32 |
33 |
34 |
35 |
| 36 |
37 |
38 |
39 |
40 |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
右端の列、即ち、5で割り切れる数はすべてAに入っ
ている。それ以外の列は、どこかで8の倍数が現れ、
それ以後はすべてAに入る。
右端以外の各列で最初に現れる8の倍数のうち最も
遅く現れるのは、32である。
従って、Aに入っていない最大の数は、32の現れる
列で、32の上にある27である。
即ち、28以上の整数はすべてAに属する。
各列には8の倍数がただ1つ存在し、しかも全て異なる。
よって、8、2・8、3・8、4・8 の各項を5で割った商の総和を求めればよい。
「8」のある列の項で、5x+8y の形で表されない項の数は、
8÷5=1 ・・・ 3
より、1個である。同様にして、「16」、「24」、「32」 のある項で、5x+8y
の形で表されな
い項の数は、
2・8÷5=3 ・・・ 1 、 3・8÷5=4 ・・・ 4 、 4・8÷5=6 ・・・ 2
より、3個、4個、6個あるので、求める場合の数は、
1+3+4+6=14 (個)
となる。これは、次のように計算してもよい。[x] をガウス記号として、
[8/5]+[2・8/5]+[3・8/5]+[4・8/5]=1+3+4+6=14 (個)
このことから、
a、b を互いに素な自然数とする。0以上の整数 x、y を使って ax+byの形で表す
ことができない自然数の個数を求めよ。
の解は、
[a/b]+[2・a/b]+[3・a/b]+・・・+[(b−1)・a/b]
と書けることが分かる。
(コメント) 上式をもっと簡潔に表すことはできないだろうか...?
FNさんより、「a で割った余りが r である列と、a−r である列をペアにして考えては...」
とアドバイスをいただきました。(平成22年11月13日付け)
FNさんからいただいたヒントをもとに、再度考えてみました。
(解) a、2a、3a、・・・、(b−1)a の各数を b で割った余りは、1、2、3、・・・、b−1
の何
れかで、互いに1対1に対応する。このとき、求める場合の数は、
[{a+2a+3a+・・・+(b−1)a}−{1+2+3+・・・+(b−1)}]/b
=(a−1){1+2+3+・・・+(b−1)}/b
=(a−1)(b−1)/2
で与えられる。
したがって、ax+by の形で表すことができない自然数の個数は、
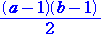
である。 (終)
(コメント) 解が綺麗に求まりましたね!FNさんに感謝します。あとねこさんにも、解が正し
いことを追認していただきました。(平成22年11月14日付け)
FNさんより、証明をいただきました。(平成22年11月14日付け)
(証明) ax+by の形で表される数の集合をAとする。0<r<b として、b
で割って r 余る数
r 、 b+r 、 2b+r 、 ・・・ 、 (a−1)b+r
を考える。この中に、a
の倍数になるものがただ1つある。それを、 kb+r とする。
このとき、この中でAに属さないものは、r から (k−1)b+r までのk
個ある。
同様に、b で割って、b−r
余る数
b−r 、 b+b−r=2b−r 、 3b−r 、 ・・・ 、 ab−r
の中に、a
の倍数になるものがただ1つある。それを、lb−r とする。
このとき、この中でAに属さないものは、b−r から (l−1)b−r までのl−1
個ある。
kb+r≡0 (mod a) 、lb−r≡0 (mod a) より、 (k+l)b≡0 (mod a)
a と b
は互いに素であるから、 k+l≡0 (mod a)
ここで、 0≦k≦a−1 、 1≦l≦a より、 1≦k+l≦2a−1 なので、
k+l=a すなわち、 k+l−1=a−1
b
で割って余りが r、a−r であるもののうちで、Aに属さないものが
k+l−1=a−1(個)
ある。 a と b は互いに素なので、少なくとも一方は奇数である。そこで、b
を奇数に取ってお
くと、余りが 1 と b−1で a−1個、2 と a−2で a−1個、・・・ となり、全部で、
(a−1)(b−1)/2 個
である。 (証終)
(コメント) 各列毎の項数がきちんと求められるんですね!求める自信がなかったので、上
記のようなアバウトな証明にしてしまいました。FNさんの精緻な証明に感動しまし
た。
FNさんに、今までのことをまとめていただきました。
次の2つが証明できたことになる。
(1A) a、b を互いに素な自然数とする。0以上の整数 x、y を使って、ax+byの形
で表せない最大の整数は、ab−a−b=(a−1)(b−1)−1 である。
従って (a−1)(b−1)以上の整数は、すべて ax+by (x,y は0以上の整数)の形に表す
ことができる。
(2A) a、b を互いに素な自然数とする。0以上の整数 x、y を使って、ax+byの形
で表せない自然数は、(a−1)(b−1)/2個ある。
x、y は0以上の整数ですが、これを、x、y
が自然数に変えたのもやっておきましょう。
(1A)(2A)からすぐ出ますが(1A)(2A)を使わないで証明するのも面白いです。
(1B) a、b を互いに素な自然数とする。自然数 x、y を使って、ax+by の形で表せ
ない最大の整数は、「?」である。
(2B) a、b を互いに素な自然数とする。自然数 x、y を使って、ax+by の形で表せ
ない自然数は、「?」個ある。
2つの場合が済めば3つの場合を考えたくなります。
自然数 a、b、c の最大公約数は1であるとする。
0以上の整数 x 、 y 、z を使って、ax+by+cz の形で表せない最大の整数を求め
よ。
これは大変難しそうで、2個の場合のような簡単な式で表すことは、とてもできそうにありま
せん。 a、b、c にもっと強い制限をつけてもいいですから、なんらかの結果はでないでしょう
か。とりあえず具体的な数で調べてみましたが何もわかりません。
攻略法さんが、FNさんの問いかけに答えられた。(平成22年11月16日付け)
(1B)(2B)の「?」は次の通りである。
(1B) ab
(2B) (a+1)(b+1)/2−1=(ab+a+b−1)/2
(2A)より、ab 以下の自然数のうちで、ax+by (x、y
は、0以上の整数)で表せな
い数は、(a−1)(b−1)/2個ある。
さらに、y=0 のとき、a の倍数 a、2a、・・・、a(b−1)、ab は、b
個
x=0 のとき、b の倍数 b、2b、・・・、b(a−1)、ab は、a 個
で、abが、1個重複している。
よって、 (a−1)(b−1)/2+b+a−1=(ab−a−b+1+2b+2a−2)/2
=(ab+a+b−1)/2
自然数 a、b、c の最大公約数は1であるとする。
0以上の整数 x 、 y 、z を使って、ax+by+cz の形で表せない最大の整数を求め
よ。
については、
a、b が互いに素で、c=ma+nb (m、n
を0以上の整数)と表される場合、ab−(a+b)
上記で得られた公式を用いると、次の問題も容易だろう。
東洋大学 工学部(1992)
m、n が負でない整数のとき、9m+10n で表せない正の整数の個数を求めよ。
また、その中の最大整数を求めよ。
(解) 9m+10n で表せない正の整数の個数は、
(9−1)(10−1)/2=36(個)
9m+10n で表せない正の整数のうち、最大な整数は、
(9−1)(10−1)−1=71 (終)
冒頭の問題は、第10回 日本数学オリンピック予選問題(平成12年)で、
3a+5b (ただし, a, b は 0 以上の整数) の形で表わせない自然数の最大値を求
めよ。
として出題されている。
(追記) 令和2年7月30日付け
問題 4と7の足し算だけで表せない整数が存在する。例えば、
1、2、3、5、6、・・・ など。
実は、このような数には、最大値が存在する。それは何か?
この問いかけを数学的に定式化すると、
0以上の整数x、yに対して、 4x+7y の形で書けない最大の整数を求めよ。
| 1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
| 17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
答えは、17 である。
以下、工事中
