2次曲線 
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(平成24年6月13日付け)
2次曲線では有名な証明問題です。
2次曲線の1つの焦点Fを通る弦の両端をP、Qとするとき、
1/FP+1/FQ
は弦の方向に関係なく一定である。
これを証明せよ。
(答) 2次曲線は、定点Fと、点Fを通らない定直線Lからの距離の比が一定な点Pの軌跡と定
義される。
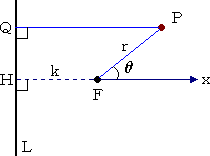
今、点Fから直線Lに下ろした垂線の足をHとし、その垂線の長さ(FH)を、kとおく。右図
のように、Fを極とし、HFの方向に始線を定める。
点Pより直線Lに下ろした垂線の足をQとするとき、
定義より、
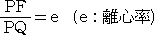
である。
右図より、 PQ=k+rcosθ なので、この式に、
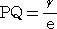
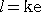
を代入して整理すれば、次のような極方程式が得ら
れる。 |
|
 |
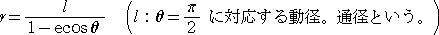
ここで、0<e<1
のとき、楕円、e=1 のとき、放物線、e>1 のとき、双曲線を表す。
また、定点Fを焦点、定直線Lを準線という。
このことから、
1/FP+1/FQ=(1−ecosθ)/l+(1−ecos(θ+π))/l=2/l(=一定)
と示される。
よおすけさんからのコメントです。(平成24年6月15日付け)
2次曲線が楕円の場合、1/FP+1/FQが弦の方向に関係なく一定であることは、以下のよう
にできます。
PQを、x=c+tcosα、y=tsinαとし、楕円の方程式 x2/a2+y2/(a2-c2))=1 に代入すると、
(a2-c2)(c+tcosα)2+(atsinα)2=a2(a2-c2)
すなわち、 (a2-c2(cosα)2)t2+2ct(a2-c2)cosα-(a2-c2)2=0
この2つの解を、t[1]、t[2]とすると、 FP=|t[1]|、FQ=|t[2]|より、
1/FP+1/FQ=(|t[1]|+|t[2]|)/(|t[1]|×|t[2]|)
ここで、 t[1]×t[2]<0 だから、 |t[1]|+|t[2]|=|t[1]-t[2]|
これを2乗して、
(t[1]-t[2])2={(2c(a2-c2)cosα)/(a2-c2(cosα)2)}2+{(4(a2-c2)2)/(a2-c2(cosα)2}
={(4a2(a2-c2)2)/(a2-c2(cosα)2)2}
よって、 |t[1]-t[2]|={(2a(a2-c2))/(a2-c2(cosα)2)}
|t[1]×t[2]|={(a2-c2)2/(a2-c2(cosα)2)}
より、 1/FP+1/FQ=2a/(a2-c2) (一定)
(コメント) 極座標を用いた証明に慣れてしまうと、個別の証明が難しく感じられますね!

