柺愊寁嶼俀俉 丂 丂 丂丂丂 丂丂丂丂 丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽側偮乿偝傫偐傜偺弌戣偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椷榓俇擭侾寧俀俀擔晅偗乯
丂旤偟偄恾宍栤戣傪徯夘偡傞偺偱丄傛偐偭偨傜夝偄偰傒偰偔偩偝偄丅嶼悢偲偟偰夝偗傑偡丅
丂摍媟戜宍ABCD偵偍偄偰丄AD//BC丂丄佢ABC亖佢DCB亖45亱丄佢ACB亖15亱丄
佢ACD亖30亱丄AD亖10cm丂偲偡傞丅
丂丂
偙偺偲偒丄巐妏宍ABCD偺柺愊偼丠
乮摎乯丂柺愊亖俆侽乮們倣2乯
丂幚嵺偵丄壓恾偵偍偄偰丄丂俹俙亖俆 丂偱丄仮俙俹俠偵偍偄偰丄俹俠亖俆
丂偱丄仮俙俹俠偵偍偄偰丄俹俠亖俆
丂丂
傛偭偰丄俹俛亖俆 丂偐傜丄俙俛亖俆乮
丂偐傜丄俙俛亖俆乮 亅
亅 乯丂偲側傞偺偱丄丂捈妏嶰妏宍俙俛俫偵偍偄偰丄
乯丂偲側傞偺偱丄丂捈妏嶰妏宍俙俛俫偵偍偄偰丄
丂倛亖俆乮 亅侾乯丂偲側傞丅偙傟偑丄摍媟戜宍偺崅偝偲側傞丅
亅侾乯丂偲側傞丅偙傟偑丄摍媟戜宍偺崅偝偲側傞丅
傛偭偰丄摍媟戜宍俙俛俠俢偺柺愊偼丄
丂乮俀倛亄侾侽亄侾侽乯亊倛亊乮侾/俀乯亖俆乮 亄侾乯亊俆乮
亄侾乯亊俆乮 亅侾乯亖俆侽乮們倣2乯丂丂乮廔乯
亅侾乯亖俆侽乮們倣2乯丂丂乮廔乯
丂夡傟偨斷偝傫偐傜丄夝摎傪偛搳峞偄偨偩偒傑偟偨丅乮椷榓俇擭侾寧俀俀擔晅偗乯
丂懡暘丄柾斖夝摎偠傖側偄偲巚偄傑偡偑丏丏丏丅
丂摍媟戜宍俙俛俠俢傪係偮巊偭偰丄俛俠傪侾曈偲偟偨惓曽宍偲俙俢傪侾曈偲偟偨惓曽宍傪嶌傝傑偡丅
奜懁偺惓曽宍傪斀帪寁夞傝偵俛俠俤俥丄撪懁偺惓曽宍傪斀帪寁夞傝偵俙俢俧俫偲偟傑偡丅
丂偙偙偱丄俢偐傜俛俠偵悅慄傪壓傠偟丄偦偺懌傪 俬 偲偡傞偲丄仮俢俬俠偼捈妏擇摍曈嶰妏宍傛傝丄
曈俙俛偺奜懁偵堏摦偝偣丄揰 俬 偺峴偒愭傪俰偲偡傞偲丄巐妏宍俰俛俬俢偼挿曽宍偵側傝傑偡丅
傑偨丄俙俫偺墑挿偲俥俤偲偺岎揰傪俲丄俫俧偺墑挿偲俤俠偲偺岎揰傪俴偲偡傞偲丄巐妏宍俥俰俙俲丄
巐妏宍俲俫俴俤丄巐妏宍俧俬俠俴偼奆丄挿曽宍俰俛俬俢偲崌摨側挿曽宍偵側傝丄懳徧惈偐傜丄巐妏
宍俲俰俬俴偼惓曽宍偵側傝傑偡丅
丂丂
丂偲偙傠偱丄俛俙偺墑挿偲俠俢偺墑挿偲偺岎揰傪俷偲偡傞偲丄俷偼惓曽宍俛俠俤俥偺拞怱偱丄
佢俛俷俠亖俋侽亱丂懄偪丄佢俙俷俠亖俋侽亱丄佢俷俠俙亖俁侽亱傛傝丄仮俷俙俠偼丄俁侽亱丄俇侽亱丄
俋侽亱偺捈妏嶰妏掕婯宆偵側傝傑偡丅
傛偭偰丄俷俙 丗 俙俠亖侾 丗 俀丂傛傝丄俷俙亖 倶 乮們倣乯丂偲抲偔偲丄俙俠亖俀倶 乮們倣乯
傑偨丄俰俬亖俙俠丂傛傝丄俰俬亖俀倶 乮們倣乯
丂偲偙傠偱丄媮傔偨偄偺偼丄戜宍俙俛俠俢亖挿曽宍俰俛俬俢亖仮俰俢俬亊俀丂傛傝丄
丂(惓曽宍俲俰俬俴亅惓曽宍俙俢俧俫)亐係亊俀丂丒丒丒丂仚丂傪媮傔傟偽椙偄丅
傛偭偰丄{(俀倶)(俀倶)亅侾侽丒侾侽}亐係亊俀亖(係倶2亅侾侽侽)亐俀丂丒丒丒丂嘆
傑偨丄仮俷俙俢亖倶2/俀丂偱丄仮俷俙俢亖侾侽2/係亖俀俆乮們倣2乯丂傛傝丄倶2亖俆侽乮們倣2乯丂丒丒丒丂嘇
嘇傪嘆偵戙擖偡傞偲丄摎偊偼丄(係亊俆侽亅侾侽侽)亐俀亖俆侽乮們倣2乯丂丂乮廔乯
仈柾斖夝摎偼僄儗僈儞僩側偺偱偟傚偆偹丅柾斖夝摎偵婜懸偟偰偄傑偡丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俀擔晅偗乯
丂側偮偝傫偺栤戣偼丄夡傟偨斷偝傫偺夝摎偐傜丄偍拑偺娫僋僀僘仌僷僘儖乽巐妏宍偺柺愊乿
偑椶戣偵側傞偲巚偄傑偡丅
仸乽巐妏宍偺柺愊乿偺UP擔偼丄暯惉俀俈擭侾俀寧俀擔晅偗
丂側偮偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俀擔晅偗乯
丂奆偝傫偁傝偑偲偆偛偞偄傑偡丅摎偊偼丄俆侽乮們倣2乯偱崌偭偰偍傝傑偡丅
丂夡傟偨斷偝傫偺夝朄偼丄嶼悢偱媮傑傞晹暘偲媮傑傜側偄晹暘傪婑傝暘偗偰偄偔傛偆側姶偠側
偺偱丄偁傞堄枴偱杮幙揑側夝偒曽偱偡偹丒丒丒両
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俁擔晅偗乯
丂嶼悢揑夝朄偼偄偔偮偐巚偄偮偒傑偟偨偑丄崱偺偲偙傠偦偺拞偱堦斣鉟楉側偺傪搳峞偟傑偡丅
庤墳偊揑偵偼傕偭偲鉟楉側夝朄傕柊偭偰偦偆側姶偠偑偟傑偡偑丏丏丏丅
丂曈 BC 忋偵 佢DAE = 30亱 偲側傞傛偆偵揰 E 傪偲傞偲丄EC = AE = 2*乮戜宍偺崅偝乯 偱偁傞
偙偲偐傜丄揰 E 偼丄幚偼 BE = 10 cm 偲側傞揰偵側偭偰偄傑偡丅
丂傛偭偰丄仮ABE 偲仮ADC 偺柺愊偼摍偟偄偙偲偑傢偐傝傑偡丅
丂偟偨偑偭偰丄戜宍 ABCD 偺柺愊偼丄乽仮ABE 2 偮偲仮AEC 偺柺愊偺崌寁乿傪弌偣偽偄偄
偙偲偵側傝傑偡丅
丂偲偙傠偱丄偙傟傜 3 偮偺嶰妏宍傪暲傋懼偊傟偽丄掙曈偲崅偝偑偲傕偵 10 cm 偺捈妏擇摍曈
嶰妏宍偵側傝傑偡丅
丂偮傑傝丄偦偺柺愊偺崌寁偼丄 10*10*(1/2) = 50 乮們倣2乯 偱偡丅
乮僐儊儞僩乯丂DD++ 偝傫偺夝朄傪恾帵偡傞偲丄
| 丂 |
 |
丂 |
 |
丂捈妏俀摍曈嶰妏宍偑鉟楉偵慻傒忋偑傞傫偱偡偹両姶摦偟傑偟偨丅傑偝偵嶼悢揑偱偡偹丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俁擔晅偗乯
丂DD++偝傫偺夝朄丄慺惏傜偟偄偱偡偹丅堦墳丄夝愢偝偣偰壓偝偄丅
丂曈 BC 忋偵 佢DAE = 30亱 偲側傞傛偆偵揰 E 傪偲傞偲丄EC = AE = 2*乮戜宍偺崅偝乯 偱偁傞
偙偲偐傜丄揰 E 偼丄幚偼 BE = 10 cm 偲側傞揰偵側偭偰偄傑偡丅
丂佢俤俙俠亖俁侽亱亅侾俆亱亖侾俆亱丄佢俤俠俙亖侾俆亱傛傝丄仮俤俙俠偼丄掙妏偑侾俆亱偺擇摍曈
嶰妏宍丅傛偭偰丄俙俤亖俠俤丂偲側傞丅
傑偨丄俤偐傜俙俢偵悅慄傪壓傠偟丄偦偺懌傪俫丄俢偐傜俤俠偵悅慄傪壓傠偟丄偦偺懌傪 俬 偲偡傞偲丄
仮俙俤俫偼俁侽亱丄俇侽亱丄俋侽亱偺捈妏嶰妏掕婯宆傛傝丄俤俫 丗 俙俤亖侾 丗 俀
傛偭偰丄俤俫 丗 俠俤亖侾 丗 俀丂傛傝丄俢俬 丗 俠俤亖侾 丗 俀丄佢俢俠俬亖係俆亱丄俢俬佦俤俠傛傝丄仮俢俤俠
偼捈妏擇摍曈嶰妏宍偱偁傞丅
乮尩枾偵偼丄仮俢俬俠偑捈妏擇摍曈嶰妏宍傛傝丄俢俬亖俠俬 偱丄俢俬 丗 俠俤亖侾 丗 俀傛傝丄俢俬亖俤俬
傑偨丄佢俢俬俤亖俋侽亱傛傝丄仮俢俬俤 傕捈妏擇摍曈嶰妏宍偩偐傜丅乯
傛偭偰丄佢俢俤俠亖係俆亱丄佢俙俛俠亖係俆亱傛傝丄俙俛//俢俤丂傑偨丄俙俢//俛俤 側偺偱丄
巐妏宍俙俛俤俢偼暯峴巐曈宍偱偁傞丅傛偭偰丄俛俤亖俙俢亖侾侽乮們倣乯
丂傛偭偰丄仮ABE 偲仮ADC 偺柺愊偼摍偟偄偙偲偑傢偐傝傑偡丅
丂偟偨偑偭偰丄戜宍 ABCD 偺柺愊偼丄乽仮ABE 2 偮偲仮AEC 偺柺愊偺崌寁乿傪弌偣偽偄偄
偙偲偵側傝傑偡丅
丂偲偙傠偱丄偙傟傜 3 偮偺嶰妏宍傪暲傋懼偊傟偽丄掙曈偲崅偝偑偲傕偵 10 cm 偺捈妏擇摍曈
嶰妏宍偵側傝傑偡丅
丂俤偐傜俛俠偵懳偟偰悅慄傪棫偰丄俛俙偺墑挿偲偺岎揰傪俥偲偡傞偲丄仮俤俛俥偼捈妏擇摍曈嶰
妏宍偱丄俛俥忋偵俥俧亖俛俙偲側傞揰俧傪庢傞偲丄仮俙俛俤偲仮俧俥俤偼崌摨丅
傑偨丄嶖妏傛傝丄佢俙俤俛亖佢俤俙俢亖俁侽亱丄佢俙俛俤亖係俆亱傛傝丄
佢俤俙俧亖俁侽亱亄係俆亱亖俈俆亱
傛偭偰丄懳徧惈傛傝丄仮俤俙俧偼丄捀妏偑俁侽亱偺擇摍曈嶰妏宍偵側傞丅
偙偙偱丄仮俤俙俠偼掙妏偑侾俆亱偺擇摍曈嶰妏宍傛傝丄敿暘偵愗偭偰慻傒捈偡偲丄仮俤俙俧偺強
偵傄偭偨傝偲偼傑傞丅
傛偭偰丄戜宍俙俛俠俢傪 仮俙俛俤亖仮俠俙俢 偲 仮俤俙俠 偵暘偗偰摍愊曄宍偡傞偲丄仮俤俛俥偲摍愊
偵側傝丄仮俤俛俥偼丄摍曈偑侾侽們倣偺捈妏擇摍曈嶰妏宍傛傝丄侾侽亊侾侽亐俀亖俆侽乮們倣2乯
傛偭偰丄摎偊偼丄俆侽乮們倣2乯
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂屻敿丄側傫偐撲偺柪憱傪巒傔偰傑偡偑戝忎晇偱偟傚偆偐丠
丂乽偙傟傜 3 偮偺嶰妏宍傪暲傋懼偊傟偽掙曈偲崅偝偑偲傕偵 10 cm 偺捈妏擇摍曈嶰妏宍偵
側傝傑偡丅乿
偼暥帤捠傝偺憖嶌偱偟偐側偔丄撲偺摍愊曄宍偩偺偝傜側傞愗抐偩偺偼晄梫偱偡傛丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂場傒偵丄乽曈 BC 忋偵 佢DAE = 30亱 偲側傞傛偆偵揰 E 傪偲傞乿戙傢傝偵丄D偐傜AB偲暯峴
側捈慄傪堷偄偰揰E傪掕傔偰傕弌棃傑偡偑丄偐側傝柺搢廘偄偱偡偹丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂杮摉偵偱偒傑偡偐丠AB//DE 偐傜 佢DAE = 30亱 傪摫偔偙偲偼偍偦傜偔晄壜擻偩傠偆偲巹偼
巚偭偰偄傑偡偑丏丏丏丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂偊偊丄暯峴巐曈宍俙俛俤俢傪嶌偭偨屻偵丄俛俢傪侾曈偲偟偨惓嶰妏宍俥俛俢傪捀揰俥偑俛俢偵娭
偟偰揰俙懁偵嶌傝丄俙俤偲俛俢偺岎揰傪俧偲偟偰丄俥俧傪寢傇偲丄岺晇師戞偱丄佢俛俙俷亖侾侽俆亱
偲媮傑傞偺偱丄佢俤俙俠亖佢俤俠俙亖侾俆亱偲媮傑傝傑偡丅
丂偨偩偟丄忋偵傕彂偒傑偟偨偑丄偪傚偭偲柺搢廘偄偺偱幚愴岦偒偱偼偁傝傑偣傫丅
丂嶼悢揑夝朄偼偄偔偮偐巚偄偮偒傑偟偨偑丄崱偺偲偙傠偦偺拞偱堦斣鉟楉側偺傪搳峞偟傑偡丅
丂庤墳偊揑偵偼傕偭偲鉟楉側夝朄傕柊偭偰偦偆側姶偠偑偟傑偡偑丄惁偄偱偡傛偹丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂AB//DE 偐傜 佢DAE = 30亱 傪摫偔
丂乽佢ABD=15亱丄佢DBC=30亱丄佢BCA=90亱丄佢ACD=45亱偱偁傞巐妏宍ABCD偵偍偄偰
佢ADB傪媮傔傞乿偲偄偆儔儞僌儗乕偺栤戣偵側傝傑偡偺偱丄壗傜偐偺偆傑偄夝朄偼偁傞偲巚偄
傑偡丅乮嶼悢偺斖埻偱夝偗傞偐偳偆偐偼傢偐傝傑偣傫偑乯
丂偆傑偔側偄揤壓傝揑夝朄偱傛偗傟傁丄埲壓偺傛偆偵偼偱偒傑偡丅
丂拞怱偑O偺墌偵撪愙偡傞惓廫擇妏宍ABCDEFGHIJKL偵偍偄偰丄捈慄BF偲捈慄LH偺嫍棧
偼墌偺敿宎偵摍偟偄偺偱丄OA偺悅捈擇摍暘慄偲BF丄LH偺岎揰傪弴偵M丄N偲偡傞偲丄巐妏
宍AMON偼惓曽宍丅偦偟偰丄嶰妏宍ACO偼惓嶰妏宍側偺偱丄巐妏宍BCMA偼忋婰偺儔儞僌
儗乕偺栤戣偺巐妏宍ABCD偺恾偲摍偟偔丄摎偊偼丄15亱
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂傜偡偐傞偝傫丄偁傝偑偲偆偛偞偄傑偡丅
丂巐妏宍BCMA偑杮戣偺恾偺巐妏宍ECDA偵摉偨傝丄佢EAC偑侾俆亱乮傜偡偐傞偝傫偺恾偱
偼佢BAC乯偵側傞偲偄偆栿偱偡偹丅
丂偆偭偐傝丄巹偺曽傕嶼悢偲偄偆帠傪朰傟偰偄偨偺偱丄嶼悢偵廋惓偟傑偟偨丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俆擔晅偗乯
丂側傞傎偳丄婃挘傟偽偱偒側偔偼側偄偺偱偡偹丅偲偼偄偊丄嵟弶偐傜 佢DAE = 30亱 偱堷偗
偽曗彆慄偼 AE 偩偗偐丄挌擩偵傗傞偵偟偰傕壓掙傊偺悅慄 AH 偲偁傢偣偰 2 杮偩偗偱嵪傓
傢偗偱丄暯峴慄偐傜僗僞乕僩偡傞曽偼寢嬊柍堄枴偵傗傗偙偟偝傪憹偟偰傞偩偗側報徾偱偡丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俆擔晅偗乯
丂偊偊丄偦偺屻丄俛俤傪侾曈偲偟偨惓嶰妏宍傪昤偄偰傕弌棃傞帠偑敾柧偟傑偟偨偑丄偦傟傕柺搢
廘偄偩偗偱偡偹丅傑偀丄偦傟偑柺敀偄傫偱偡偑丅徫
乮僐儊儞僩乯丂儔儞僌儗乕偺栤戣丂仺丂乮嶲峫乯丗乽妏偺戝偒偝乮俀乯乿
丂傛偍偡偗偝傫偐傜傕夝摎傪偄偨偩偒傑偟偨丅乮椷榓俇擭侾寧俀係擔晅偗乯
丂AD//BC傛傝丄佢ACB亖佢CAD偐傜丄佢CAD=15亱
丂仮ADC偵惓尫掕棟傪揔梡偡傞偲丄AC/sin佢ADC亖AD/sin佢ACD偵偍偄偰丄
丂佢ADC亖180亱亅(佢CAD+佢ACD)亖135並丄佢ACD亖30亱丄AD亖10丂傛傝丄
丂AC亖AD亊sin135亱亐sin30亱亖10
丂仮ABC偵惓尫掕棟傪揔梡偡傞偲丄BC/sin佢BAC亖AC/sin佢ABC偵偍偄偰丄
丂佢BAC亖120並丄佢ABC亖45亱丄AC亖10 丂傛傝丄
丂傛傝丄
丂BC亖AC亊sin120亱亐sin45亱亖10
丂摍媟戜宍ABCD偺柺愊偼仮ADC偲仮ABC偺柺愊偺榓偵摍偟偄偺偱丄
摍媟戜宍ABCD亖仮ADC亄仮ABC
亖乮1/2乯丒AD丒AC丒sin佢CAD亄乮1/2乯丒AC丒BC丒sin佢ACB
亖乮1/2乯丒10丒10 丒sin15亱亄乮1/2乯丒10
丒sin15亱亄乮1/2乯丒10 丒10
丒10 丒sin15亱
丒sin15亱
亖50乮 亄
亄 乯sin15亱
乯sin15亱
亖50乮 亄
亄 乯乮
乯乮 亅
亅 乯/4
乯/4
亖50
丂傛偍偡偗偝傫偐傜捛壛偺夝摎傪偄偨偩偒傑偟偨丅乮椷榓俇擭侾寧俀俈擔晅偗乯
丂忋婰偺夝摎傛傝丄BC亖侾侽 丂偵拲栚偟偰丄摍媟戜宍ABCD偺柺愊偼丄1曈偑BC偺惓曽宍
丂偵拲栚偟偰丄摍媟戜宍ABCD偺柺愊偼丄1曈偑BC偺惓曽宍
偐傜侾曈偑AD偺惓曽宍傪彍偄偨柺愊偺1/4偵摍偟偄偺偱丄
丂(1/4)(10 亊10
亊10 亅10亊10)亖50
亅10亊10)亖50
乮嶲峫乯丂偍拑偺娫僋僀僘仌僷僘儖丗乽巐妏宍偺柺愊乿
乮暿夝乯丂AB亖CD亖俆乮 亅
亅 乯丂側偺偱丄摍媟戜宍ABCD偺係曈AB丄BC丄CD丄DA偺挿偝
乯丂側偺偱丄摍媟戜宍ABCD偺係曈AB丄BC丄CD丄DA偺挿偝
偼丄弴偵丄俆乮 亅
亅 乯丄侾侽
乯丄侾侽 丄俆乮
丄俆乮 亅
亅 乯丄侾侽丂偲側偭偨偺偱丄偙傟傪
乯丄侾侽丂偲側偭偨偺偱丄偙傟傪
僽儗乕僩僔儏僫僀僟乕偺岞幃丂乮仺丂嶲峫丗乽僽儔儅僌僾僞偺岞幃乿乯
S=併乷(s亅AB)(s亅BC)(s亅CD)(s亅DA)亅AB丒BC丒CD丒DA丒(cos^2(佢ABC亄佢CDA)/俀)乸
偨偩偟丄s亖(AB亄BC亄CD亄DA)/俀
偵擖傟傟偽丄梌偊傜傟偨摍媟戜宍ABCD偺柺愊S偼丄50
仈忋婰偺撪梕偼丄偄偢傟傕姰慡側夝摎偱偼側偄偺偱丄嶲峫掱搙偵丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂傛偆傗偔栤戣偺嶌堊夝摎偭傐偄傕偺傪尒偮偗傑偟偨丅偨偩偺戜宍偱偼側偔丄摍媟戜宍偲傢偞
傢偞彂偄偰偁傞偙偲偵丄傕偭偲拲栚偡傞傋偒偱偟偨丅
丂丂
丂偙偺巐妏宍傪 AC 偱愗抐偟丄仮ADC 傪棤曉偟偰丄嵞傃 AC 偵媡岦偒偵愙崌偟傑偡丅D偺堏
摦屻偺捀揰傕D偲昞偡偙偲偵偡傞丅
丂偡傞偲丄AB = AD丄佢ABC = 45亱丄佢BAD = 150亱丄佢ADC = 135亱丄佢BCD = 30亱偺巐
妏宍 ABCD 偑偱偒傑偡丅
丂丂
丂偙傟傪崱搙偼 BD 偱愗抐偡傞偲丄俀偮偺擇摍曈嶰妏宍偑偱偒傑偡丅偝傜偵丄偦傟傜傪丄偦傟
偧傟懳徧偵恀偭擇偮偵偡傞偲丄寢嬊丄偙偺恾宍偼丄
丒幬曈偑 10 cm丄崅偝偑 5 cm丄掙妏 30亱 偺捈妏嶰妏宍
丒崅偝偑 5 cm丄掙妏 75亱 偺捈妏嶰妏宍
偑俀枃偢偮偵側傝傑偡丅
丂偲偙傠偱丄偙傟傜 1 枃偢偮傪崅偝摨巑偑攚崌傢偣偵側傞傛偆偵揬傝崌傢偣傞偲丄
掙曈 10 cm丄崅偝 5 cm 偺擇摍曈嶰妏宍偵側傞偺偱丄
丂丂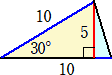
偦偺柺愊偼 10*5*(1/2) = 25乮們倣2乯
傛偭偰丄尦偺戜宍偺柺愊偼丄偦偺攞偱丄 50乮們倣2乯
乮僐儊儞僩乯丂DD++ 偝傫丄慺惏傜偟偄両
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂偝偡偑丄DD++ 偝傫丄尒帠偱偡偹丅俙俠偱愗偭偰慻傒姺偊傞偺偼偨傑偵尒傞庤朄偱偡偑丄嵟
屻偺強偺俀偮偺嶰妏宍傪侾偮偺擇摍曈嶰妏宍偵偡傞強偼扙朮偱偡丅
丂慜夞偺夝摎傕丄崱夞偖傜偄暘偐傝堈偗傟偽丄傢偞傢偞夝愢偟側偐偭偨傫偱偡偗偳偹丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂慜夞偺傕丄傎偲傫偳偑巹偼傗偭偰側偄寁嶼傪彑庤偵夡傟偨斷偝傫偑晅偗懌偟傑偔偭偰丄傗傗
偙偟偔偟偨偩偗偱偡傛丠
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂丂
乮嶼悢偺夝朄俀乯
丂俛俙偺墑挿偲俠俢偺墑挿偲偺岎揰傪俤偲偡傞偲丄仮俤俙俢偲仮俤俛俠偼憡帡偱丄嫟偵捈妏擇摍曈
嶰妏宍偵側傝丄佢俛俤俠亖俋侽亱
丂傑偨丄佢俙俠俤亖俁侽亱傛傝丄仮俠俙俤偼丄俁侽亱丄俇侽亱丄俋侽亱偺捈妏嶰妏掕婯宆偱丄俤偐傜
俙俠偵悅慄傪壓傠偟丄偦偺懌傪俫偲偡傞偲丄仮俤俙俫偲仮俠俤俫傕丄俁侽亱丄俇侽亱丄俋侽亱偺捈妏
嶰妏掕婯宆偵側傞丅
傛偭偰丄俙俫亖嘆偲偡傞偲丄俙俤亖嘇丄俙俠亖嘋傛傝丄俠俫亖嘋亅嘆亖嘊 側偺偱丄
俙俫 丗 俠俫亖侾 丗 俁丂偲側傞偐傜丄仮俤俙俫 丗 仮俤俠俫亖侾 丗 俁
傛偭偰丄仮俤俙俫佷仮俠俤俫傛傝丄俙俤亊俙俤 丗 俤俠亊俤俠亖侾 丗 俁
偲偙傠偱丄仮俤俙俢佷仮俤俛俠偱丄仮俤俙俢 丗 仮俤俛俠亖俤俙亊俤俙 丗 俤俠亊俤俠亖侾 丗 俁
傑偨丄仮俤俙俢偼丄幬曈偑侾侽們倣偺捈妏擇摍曈嶰妏宍傛傝丄仮俤俙俢亖侾侽亊俆亐俀亖俀俆乮們倣2乯
傛偭偰丄仮俤俛俠亖俀俆亊俁亖俈俆乮們倣2乯丂傛傝丄戜宍俙俛俠俢亖俈俆亅俀俆亖俆侽乮們倣2乯
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂側傫偐巹偺埲慜偺夝摎偵彑庤偵塕夝愢偮偗偨忋偱擄暼偮偗偰偔傞恖偑偄傞偺偱丄懠偺恖
偑閤偝傟側偄傛偆丄傕偆堦夞偪傖傫偲彂偄偰偍偒傑偡丅
丂埲壓偑慜夞偺夝摎偺寁嶼慡晹偱偡丅忋婰偺帺徧乽夝愢乿偼丄偰傫偱揑奜傟側寁嶼傪彑庤
偵晅偗懌偟丄偦傟偑丄偝傕廳梫偱偁傞偐偺傛偆偵殏偄偰偄傞偩偗偱偡丅偛拲堄偔偩偝偄丅
丂曈 BC 忋偵 佢DAE = 30亱 偲側傞傛偆偵揰 E 傪偲傝傑偡丅
| 丂 |
 |
丂 |
 |
丂暯峴慄偺嶖妏偑摍偟偄偙偲偐傜 佢DAC = 15亱 側偺偱丄佢EAC = 30亱 - 15亱 = 15亱 偱偡丅
偟偨偑偭偰丄仮EAC 偼擇摍曈嶰妏宍偱偁傝丄EC = EA 偱偁傞偙偲偑傢偐傝傑偡丅
傑偨丄揰 A 偐傜曉 BC 偵悅慄 AH 傪壓傠偟傑偡丅
佢EAH 偼 90亱 偐傜 佢DAC 傪堷偄偨巆傝側偺偱丄佢EAH = 90亱 - 30亱 = 60亱
傛偭偰丄仮EAH 偼撪妏偑 90亱, 60亱, 30亱 偺捈妏嶰妏宍偱偁傞偙偲偑傢偐傝丄AE 偼 AH
偺攞偺挿偝偱偁傞偙偲偑傢偐傝傑偡丅
偟偨偑偭偰丄EC 偼戜宍偺崅偝 2 偮暘偺挿偝偱偁傞偙偲偑傢偐傝傑偡丅
丂偙偺戜宍偼掙妏 45亱 偺摍媟戜宍側偺偱丄壓掙偼忋掙傛傝傕戜宍偺崅偝 2 偮暘挿偔丄BE
偼偦偺壓掙傛傝傕EC丄懄偪丄戜宍偺崅偝 2 偮暘抁偄偺偱丄BE 偼忋掙偺挿偝偲摍偟偄 10 cm
偱偁傞偙偲偑傢偐傝傑偡丅
丂偙偙偱丄仮ABE 偲 仮ADC 偵拲栚偡傞偲丄偳偪傜傕掙曈 10 cm 偱丄崅偝偼戜宍偲嫟捠偱偡丅
偡側傢偪丄偙偺 2 偮偺嶰妏宍偼摍偟偄柺愊偱偡丅
傛偭偰丄戜宍偺柺愊 = 仮ABE + 仮EAC + 仮ADC = 仮ABE*2 + 仮EAC丂傪媮傔傟偽偄偄偙
偲偵側傝傑偡丅
偲偙傠偱丄仮ABE 2 偮傪 AB 摨巑揬傝崌傢偣偰僽乕儊儔儞宆偵偡傞偲丄墯傫偱偄傞晹暘偼捀
妏 150亱 偱摍曈偑 AE 偱偁傞擇摍曈嶰妏宍偡側傢偪 仮EAC 偺宍偵側傝傑偡丅
傛偭偰丄仮ABE*2 + 仮EAC 偼摍曈 10 cm 偺捈妏擇摍曈嶰妏宍偺柺愊偵摍偟偔丄
10*10*(1/2) = 50乮們倣2乯 偱偡丅偟偨偑偭偰丄尦乆偺戜宍偺柺愊傕 50 們倣2 偱偡丅
## 崱夞偼徣棯傕偟偰偄傑偣傫偺偱丄彑庤偵曄側寁嶼傪懌偝側偄偱偔偩偝偄丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂傛偆傗偔堄恾偑暘偐傝傑偟偨丅擮偺偨傔丄幾杺傪偟偰偄傞栿偱偼偁傝傑偣傫丅
丂側偮偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂DD++偝傫偺夝偒曽偼柺敀偄偱偡偹両両嵟屻偵偆傑偔捈妏擇摍曈嶰妏宍傪嶌傞偺偑旤偟偄
偱偡偹丒丒丒両
丂彮偟榚摴偵偦傟傑偡偑丄搑拞偱弌偰偒偨
丂乽佢ABD=15亱丄佢DBC=30亱丄佢BCA=90亱丄佢ACD=45亱偱偁傞巐妏宍ABCD偵偍偄偰
佢ADB傪媮傔傞乿
偲偄偆栤戣偼丄1995擭嶼悢僆儕儞僺僢僋僩儔僀傾儖偱愝掕偝傟偰偄傞妏搙偺応強偼堘偄傑偡偑丄
摨偠恾宍偱栤戣偑弌偰偄傑偡丅
丂娙扨偵夝偔側傜偙傫側姶偠偱偡偐偹丒丒丒丠
丂丂
丂曈AC傪1曈偲偡傞惓嶰妏宍傪揰B偺斀懳懁偵嶌傝丄捀揰傪E偲抲偔丅
佢BDC亖佢DCE亖15亱側偺偱丄BD//CE丂乧丂嘆
傑偨丄BC亖AC亖EC丂偱偁傞偙偲偐傜丄仮BCE偼擇摍曈嶰妏宍偱丄佢CEB亖15亱
傛偭偰丄佢DBE亖30亱乕15亱亖15亱
佢DBE亖佢BDC亖15亱偱偁傞偙偲偲嘆傛傝丄巐妏宍BCED偼摍媟戜宍側偺偱丄
佢BCE亖佢DEC亖150亱丄BC亖DE
傕傠傕傠寁嶼偡傞偲丄仮AED偑捈妏擇摍曈嶰妏宍偱偁傞偙偲偑傢偐傝丄AB亖AD偲側偭偰丄慡
晹偺妏搙偑媮傑傝傑偡丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂側偮偝傫丄偁傝偑偲偆偛偞偄傑偡丅捈妏擇摍曈嶰妏宍傪嶌傞夝摎偺曽傕柺敀偄夝摎偵偱偒
偨偲巚偄傑偡偑丄偍偦傜偔側偮偝傫偺堄恾偟偰偄偨夝摎偼丄忋婰偵彂偄偨傕偺偱偼側偄偐偲
巚偭偰偄傑偡丅偄偐偑偱偟傚偆丠
丂側偮偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俇擔晅偗乯
丂幚偼丄憐掕夝摎偲偼堘偄傑偟偨偑丄偆傑偔媮傔傜傟傞恾宍偵曄宍偟偰偄偔丄偄偄夝偒曽偱偡
偹両幚偼丄偙偺嵟弶偺仮ACD傪斀揮偡傞曽朄偱傕擇摍曈嶰妏宍偵帩偭偰偄偔曽朄偼偄偔偮
偐偁傝偦偆偱偟偨丅
丂娙棯側徯夘偲側傝傑偡偑丄椺偊偽恾偺傛偆偵曄宍偟偰傕夝偗偦偆偱偡丅
乮杮幙偼堦弿偱偟偨両乯
丂丂
丂憐掕夝朄偼師偺傛偆側傕偺偱偟偨丅偛徯夘偝偣偰偄偨偩偒傑偡m(_ _)m
亂憐掕夝朄亃乮彮偟徣棯偟偰彂偒傑偡乯
丂巐妏宍ABCD偵奜愙偡傞墌偺拞怱傪O偲抲偔乮墌偑偍偗傞偙偲偺媍榑偼妱垽乯
丂拞怱妏偺掕棟傛傝丄佢AOB亖15亱亊2亖30亱丄摨條偵丄佢DOC亖30亱丄
丂佢AOD亖30亱亊2亖60亱
傛偭偰丄仮AOB偲仮DOC偼30亱傪捀妏偲偡傞擇摍曈嶰妏宍丄仮AOD偼惓嶰妏宍丅
偙偙偱丄仮AOD偲仮BOC傪偦傟偧傟恀傫拞偺廲慄偱敿暘偵偡傞偲丄偦傟偧傟摨偠戝偒偝偺
30亱丄60亱丄90亱偺捈妏嶰妏宍偑偱偒傞偨傔丄仮AOD偲仮BOC偺柺愊偼摍偟偄丅
乮尩枾側媍榑偼徣棯乯
偦傟偵傛傝丄巐妏宍ABCD偺柺愊偼丄仮AOB偲仮DOC偺柺愊偺崌寁偲摍偟偔側傞丅
乮屲妏宍ABOCD偺柺愊偐傜仮AOD偺柺愊傪堷偄偨傕偺偲屲妏宍ABOCD偺柺愊偐傜仮BOC
偺柺愊傪堷偄偨傕偺偑摍偟偄偨傔乯
丂仮AOB偲仮DOC偼偍側偠傒偺柺愊偑媮傔傜傟傞擇摍曈嶰妏宍偱偁傞偨傔丄
丂10cm亊5cm亐2亊2亖50乮們倣2乯 丂乮摎偊乯
嶨偵嶌偭偨恾傕嵹偣偰偍偒傑偡娋
丂丂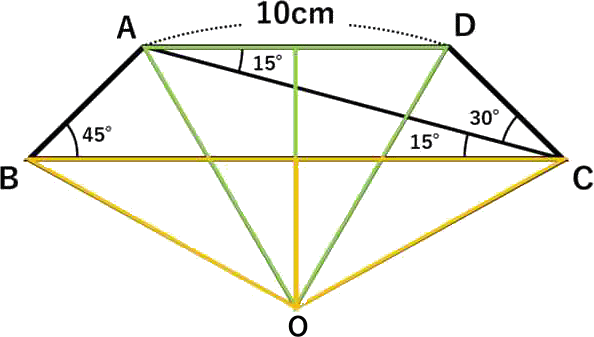
丂DD++偝傫偺偙偺夝朄偼丄偄傑偺柾斖夝摎傪巚偄偮偔傑偱偼柾斖夝摎偲偟偰偍傝傑偟偨丅嶌
栤帪偵偼偙偙偐傜栤戣傪嶌偭偨偺偱丄巹偲偟偰偼堄恾傪慻傫偱偔偩偝偭偨偲戝曄偆傟偟偔巚偭
偰偍傝傑偡丅
丂偦偺懠偺奆條傕丄條乆偵夝偄偰偔偩偝傝偁傝偑偲偆偛偞偄傑偟偨両
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俈擔晅偗乯
丂巹偼媡偵丄奜愙墌傪巊偆曽傪愭偵巚偄偮偒傑偟偨丅偨偩丄乽棳愇偵拞怱妏偺掕棟偼嶼悢奜
偐丠乿偲巚偭偰媝壓偟偪傖偭偨傫偱偡傛偹丅
丂偳偆傗傜拞怱妏傕傾儕傒偨偄側偺偱丄偦傟傪巹偺戞嶰偺夝摎偲偟偰搳峞偟傑偡丅
丂巐妏宍 ABCD 偺奜愙墌傪彂偒丄拞怱傪 O 偲偟傑偡丅
丂丂
丂拞怱妏偺掕棟傛傝 佢AOD = 60亱 側偺偱丄仮AOD 偼惓嶰妏宍偱丄偙偺奜愙墌偺敿宎偼
10 cm 偱偡丅
丂傑偨丄拞怱妏偺掕棟傛傝丄佢AOC = 90亱丄佢COD = 30亱 偱偡丅
丂偝偰丄偙偙偱 仮CAB 傪丄揰 O 傪拞怱偵 90亱 夞揮堏摦偟偰揰 C 傪揰 A 偵廳偹丄仮AEF 偲
偟傑偡丅
丂戜宍偺柺愊偼 仮ACD + 仮AEF 偱媮傑傝傑偡丅偦偟偰丄偙傟傪摍愊曄宍乮仸乯偟偰
仮OCD + 仮OEF 偲偟傑偡丅
丂偙傟傜 2 偮偼崌摨側擇摍曈嶰妏宍偱丄傕偼傗尵偆傑偱傕側偄曽朄偱 1 偮 25 們倣2 偲弌傞
偺偱丄尦偺戜宍偺柺愊偼攞偺 50 們倣2 偱偡丅
仸 2 偮偺嶰妏宍偵偮偄偰丄掙曈摨巑偑暯峴偱挿偝偑摍偟偔丄捀揰偑摨堦揰偐偮偦傟偑掙曈
丂傪墑挿偟偨暯峴慄偺娫偵偁傞応崌丄偦偺嫟捠捀揰傪暯峴慄偺娫偺偳偙傊堏摦偟偰傕 2 偮
丂偺嶰妏宍偺柺愊偺榓偼堦掕
丂側偮偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾寧俀俈擔晅偗乯
丂棳愇偵拞怱妏偺掕棟偼嶼悢奜偐丠
丂DD++ 偝傫丄偛巜揈偁傝偑偲偆偛偞偄傑偡丅偨偟偐偵拞怱妏偺掕棟偼嶼悢奜傒偨偄偱偡偹丅
偆偭偐傝愢柧側偟偵巊偭偰偟傑偭偰偍傝傑偟偨怽偟栿偛偞偄傑偣傫丅丅丅
丂墌傪巊傢偢偵傗傞偲丄偳偆偟偰傕媡愢揑側庤朄偵側偭偰偟傑偄偦偆偱偡偹丅崅偝偺崌寁偑偪傚
偆偳擇摍曈嶰妏宍俀偮暘偵側傞敪憐偼巚偄偮偒傑偣傫偱偟偨丅柺敀偄夝朄傪偁傝偑偲偆偛偞偄
傑偡両
丂丂埲壓丄岺帠拞両











