 丂
丂丂僀儞僪偺悢妛幰僽儔儅僌僾僞乮598乣660乯偼丄偲偰傕旤偟偄岞幃傪巆偟偰偄傞丅偦偟偰丄偙偺岞
幃偺偍偐偘偱丄挿擭懡彮堘榓姶偺偁偭偨乽僿儘儞偺岞幃乿偑丄幚偼昁慠揑側傕偺偱偁傞偙偲偑
棟夝偱偒偨丅僽儔儅僌僾僞偵戝偄偵姶幱偟側偗傟偽側傜側偄丅
僽儔儅僌僾僞偺岞幃
僽儔儅僌僾僞偺岞幃丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂
丂
丂僀儞僪偺悢妛幰僽儔儅僌僾僞乮598乣660乯偼丄偲偰傕旤偟偄岞幃傪巆偟偰偄傞丅偦偟偰丄偙偺岞
幃偺偍偐偘偱丄挿擭懡彮堘榓姶偺偁偭偨乽僿儘儞偺岞幃乿偑丄幚偼昁慠揑側傕偺偱偁傞偙偲偑
棟夝偱偒偨丅僽儔儅僌僾僞偵戝偄偵姶幱偟側偗傟偽側傜側偄丅
僽儔儅僌僾僞偺岞幃
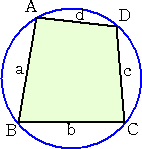 |
丂丂丂墌偵撪愙偡傞巐妏宍偺係曈偺挿偝傪丄倎丄倐丄們丄倓 偲偡傞偲偒丄 丂丂巐妏宍偺柺愊 俽 偼丄 丂丂 丂丂偱梌偊傜傟傞丅 |
乮徹柧乯丂丂俽亖仮俙俛俠亄仮俙俠俢丂偵偍偄偰丄俛亄俢亖侾俉侽亱傛傝丄倱倝値
俛亖倱倝値 D丂側偺偱丄
丂丂俀俽亖乮倎倐亄們倓乯倱倝値 俛
偙偙偱丄梋尫掕棟偵傛傝丄俙俠2亖倎2亄倐2亅俀倎倐們倧倱 俛亖們2亄倓2亅俀們倓們倧倱 俢
俛亄俢亖侾俉侽亱傛傝丄們倧倱 俢亖亅們倧倱 俛丂偱偁傞偙偲偵拲堄偟偰丄們倧倱 俛 傪媮傔傟偽丄
丂丂![]()
偲側傞丅偙偺偲偒丄
丂![]()
偲側傞偙偲偑娙扨側寁嶼偱帵偝傟傞丅
乮偙偺寁嶼偼丄場悢暘夝偺揟宆揑側寁嶼側偺偱丄徻偟偄偲偙傠偼撉幰偵傑偐偣傛偆両乯
丂倎亄倐亄們亅倓亖倎亄倐亄們亄倓亅俀倓亖俀乮倱亅倓乯丂側偳偐傜丄
丂![]()
偙傟傛傝丄倱倝値 俛 傪媮傔偰丄俀俽亖乮倎倐亄們倓乯倱倝値 俛 偵戙擖偡傟偽丄岞幃偑摼傜傟傞丅丂丂乮廔乯
丂僽儔儅僌僾僞偺岞幃偺旤偟偝偼丄壗偲偄偭偰傕丄偦偺堦條惈偵偁傞丅巐妏宍偺廃偺挿偝偺
敿暘乮倱乯偐傜堦條偵奺曈偺挿偝傪堷偄偰偄傞丅偦偙偵偼丄堦揰偺偨傔傜偄傕側偄丅
丂偦傟偵懳偟偰丄嶰妏宍偺柺愊傪媮傔傞僿儘儞偺岞幃丗
丂![]()
乮偨偩偟丄 a 丄b 丄c 偼嶰妏宍偺嶰曈偱丄倱偼丄嶰妏宍偺廃偺挿偝偺敿暘乯
偵偍偄偰偼丄偦偺堦條惈偑尒傜傟側偄丅丂倱 偺傒偑丄壗偐応堘偄側丄晄帺慠側宍偱偁傞丅
丂偙偺揰偵偮偄偰丄僿儘儞偺岞幃傪崅峑俀擭偺偲偒偵妛傫偱埲棃丄僿儘儞偺岞幃傪栚偵偡傞
搙偵婔偽偔偐偺堘榓姶傪姶偠偰偄偨丅
丂偲偙傠偑丄僽儔儅僌僾僞偺岞幃傪梡偄傟偽丄偙偺堘榓姶偼堦憒偝傟傞丅倱 偺懚嵼偵傕昁慠
惈偑偁偭偨偺偩両
丂師偺傛偆偵峫偊傟偽傛偄丅
丂嶰妏宍傪丄係曈偺偆偪偺侾曈偺挿偝偑 侽 偺巐妏宍偲峫偊傞丅偟偐傕丄嶰妏宍偵偼昁偢奜愙
墌偑懚嵼偡傞偺偱丄僽儔儅僌僾僞偺岞幃偵偍偗傞忦審偼枮偨偝傟傞丅
丂傛偭偰丄僽儔儅僌僾僞偺岞幃偵傛傝丄嶰妏宍偺柺愊偼丄
丂![]()
偲棟夝偝傟傞丅偙偺傛偆偵峫偊傞偲丄傗偼傝丄僿儘儞偺岞幃偵偍偄偰傕丄堦條惈偑偁傞偲擣幆
偣偞傞傪摼側偄丅
乮嶲峫暥專丗丂俢丏僂僃儖僘丂挊丂戝嫶媊朳丂栿丂傒偮偗傛偆両悢妛両乮娾攇彂揦乯
丂丂丂丂丂丂丂丂塱堜桬堦丂挊丂俁妏娭悢丂乮壢妛怴嫽幮儌僲僌儔僼乯乯
乮捛婰乯丂倠倱 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俈擭俁寧侾俈擔晅偗乯
丂僿儘儞偺岞幃 S丱俀亖倱(s-a)(s-b)(s-c) 偺奼挘偲偟偰丄僽僞乕儅僌僾僞偺岞幃偑偁傝傑偡丅
丂S^2=(s-a)(s-b)(s-c)(s-d) 偱丄d=0 偲偡傟偽摼傜傟傑偡丅
丂偙傟偼撪愙巐妏宍偺応崌偱偡偑丄撪愙偟側偄巐妏宍偵偮偄偰丄
僽儗乕僩僔儏僫僀僟乕偺岞幃
丂S^2=(s-a)(s-b)(s-c)(s-d)乕abcdcos^2(A+C)/2
偑抦傜傟偰偄傑偡丅乮壓婰嶲徠乯
丂倠倱 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俈擭俁寧俀侽擔晅偗乯
丂撌巐妏宍ABCD偺応崌丄曈AB偺拞揰傪E丄BC偺拞揰傪F丄CD偺拞揰傪G丄DA偺拞揰傪H偲
抲偒傑偡丅揰E偲揰G傪傪寢傫偩慄暘忋偵丄揰F偐傜偺悅慄偺懌傪P丄揰H偐傜偺悅慄偺懌傪
Q偲偟傑偡丅
丂丂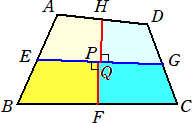
丂偡傞偲丄嵸抐偟偰丄巐妏宍AEQH傪E傪拞怱偵丄巐妏宍HQGD傪G傪拞怱偵夞揮偟丄挿曽宍
偑弌棃偰丄
丂巐妏宍ABCD偺柺愊S亖俀EG丒HQ亖俀EG丒FP亖EG乮HQ亄FP乯
傪抦傝丄姶摦偟傑偟偨丅
丂嵸抐偵傛傝丄惓嶰妏宍傪惓曽宍偵偡傞偙偲傕丄偡偛偄偱偡偹!
乮僐儊儞僩乯丂幚嵺偵嵸抐偟偰宷偓崌傢偣傞偲丄
丂丂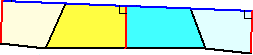
偲榗傫偱偄傑偟偨丅乽AD偲俛俠偑暯峴乿偲偄偆忦審偑偁傟偽丄挿曽宍偑弌棃偦偆偱偡丅
丂忋恾傪偝傜偵夞揮偝偣偰丄
丂丂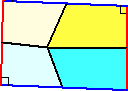
偲偄偆偙偲偐側丠俥丄俫偑悅慄偺懌側傜挿曽宍偑弌棃偦偆偱偡偑丏丏丏丠
乮捛婰乯丂忋婰偱僽儔儅僌僾僞偺岞幃偵偮偄偰徯夘偟偨偑丄嵟嬤偦偺堦斒壔偑懚嵼偡傞偙偲傪
丂丂丂抦偭偨丅乮暯惉侾俉擭俀寧侾侾擔晅偗乯
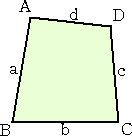 |
丂丂丂巐妏宍俙俛俠俢偺係曈偺挿偝傪丄倎丄倐丄們丄倓 偲偟丄 丂丂丂丂丂丂丂倎亄倐亄們亄倓亖俀倱丂丂丄丂俙亄俠亖俀兤 丂丂偲偡傞丅偙偺偲偒丄巐妏宍俙俛俠俢偺柺愊 俽 偼師偺幃偱梌偊傜傟傞丅 丂丂丂丂 |
丂忋婰偵偍偄偰丄摿偵巐妏宍俙俛俠俢偑墌偵撪愙偡傞偲偒丄墌偵撪愙偡傞巐妏宍偺惈幙偐傜丄
俙亄俠亖侾俉侽亱側偺偱丄兤亖俋侽亱偡側傢偪丄們倧倱兤亖們倧倱俋侽亱亖侽丂側偺偱丄僽儔儅僌僾僞偺
岞幃偑偊傜傟傞丅
乮捛婰乯丂俫俶乽捠傝偡偑傝乿偝傫偐傜丄乽堦斒壔偝傟偨僽儔儅僌僾僞偺岞幃乿偺柤慜偼乽僽儗乕僩
丂丂丂僔儏僫僀僟乕偺岞幃乿偲尵傢傟傞偙偲傪偛嫵帵捀偄偨丅乮暯惉俀俈擭侾侽寧侾侾擔晅偗乯
丂偙偺堦斒壔偝傟偨僽儔儅僌僾僞偺岞幃偺徹柧傪峫偊偰傒傛偆丅
乮徹柧乯丂俽亖仮俙俛俢亄仮俛俠俢亖(1/2)倎倓丒倱倝値俙亄(1/2)倐們丒倱倝値俠丂傛傝丄
丂俀俽亖倎倓丒倱倝値俙亄倐們丒倱倝値俠
椉曈傪暯曽偟偰丄丂係俽2亖倎2倓2丒倱倝値2俙亄俀倎倐們倓丒倱倝値俙倱倝値俠亄倐2們2丒倱倝値2俠丂丒丒丒乮侾乯
偙偙偱丄梋尫掕棟傛傝丄俛俢2亖倎2亄倓2亅 俀倎倓丒們倧倱俙亖倐2亄們2亅 俀倐們丒們倧倱俠丂側偺偱丄
丂倎2亅倐2亅們2 亄倓2亖俀倎倓丒們倧倱俙亅 俀倐們丒們倧倱俠
傛傝丄丂乮倎2亅倐2亅們2 亄倓2乯/俀亖倎倓丒們倧倱俙亅 倐們丒們倧倱俠丂偱丄椉曈傪暯曽偟偰丄
乮倎2亅倐2亅們2 亄倓2乯2/係亖倎2倓2丒們倧倱2俙亅俀倎倐們倓丒們倧倱俙們倧倱俠亄倐2們2丒們倧倱2俠丂丒丒丒乮俀乯
乮侾乯亄乮俀乯傛傝丄
丂係俽2亄乮倎2亅倐2亅們2 亄倓2乯2/係
亖倎2倓2亅俀倎倐們倓丒們倧倱乮俙亄俠乯亄倐2們2
亖倎2倓2亅俀倎倐們倓丒們倧倱俀兤亄倐2們2
亖倎2倓2亅俀倎倐們倓丒乮俀們倧倱2兤亅侾乯亄倐2們2
亖乮倎倓亄倐們乯2亅係倎倐們倓丒們倧倱2兤
傛偭偰丄丂侾俇俽2亄乮倎2亅倐2亅們2 亄倓2乯2亖係乮倎倓亄倐們乯2亅侾俇倎倐們倓丒們倧倱2兤丂傛傝丄
侾俇俽2
亖係乮倎倓亄倐們乯2亅乮倎2亅倐2亅們2 亄倓2乯2亅侾俇倎倐們倓丒們倧倱2兤
亖(俀倎倓亄俀倐們亄倎2亅倐2亅們2 亄倓2)(俀倎倓亄俀倐們亅倎2亄倐2亄們2 亅倓2)亅侾俇倎倐們倓丒們倧倱2兤
亖乷乮倎亄倓乯2亅乮倐亅們乯2 乸乷乮倐亄們乯2亅乮倎亅倓乯2乸亅侾俇倎倐們倓丒們倧倱2兤
亖(倎亄倓亄倐亅們)(倎亄倓亅倐亄們)(倐亄們亄倎亅倓)(倐亄們亅倎亄倓)亅侾俇倎倐們倓丒們倧倱2兤
亖(俀倱亅俀們)(俀倱亅俀倐)(俀倱亅俀倓)(俀倱亅俀倎)亅侾俇倎倐們倓丒們倧倱2兤
亖侾俇(倱亅倎)(倱亅倐)(倱亅們)(倱亅倓)亅侾俇倎倐們倓丒們倧倱2兤
丂埲忋偐傜丄丂俽2亖(倱亅倎)(倱亅倐)(倱亅們)(倱亅倓)亅倎倐們倓丒們倧倱2兤丂偲側傝丄
丂![]()
傪摼傞丅丂丂乮徹廔乯
丂堦斒壔偝傟偨僽儔儅僌僾僞偺岞幃偐傜丄摿偵巐妏宍偑墌偵撪愙偡傞応崌偲偟偰丄僽儔儅僌
僾僞偺岞幃偑摫偐傟偨偑丄偦傟偱偼丄巐妏宍偑墌偵奜愙偡傞応崌偼丄偳傫側岞幃偑摫偐
傟傞偺偩傠偆偐丠嫽枴偺庬偼恠偒側偄丅
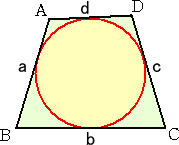 |
丂墌偵奜愙偡傞巐妏宍偺係曈偺挿偝傪丄倎丄倐丄們丄倓 偲偟丄 丂丂丂丂丂丂倎亄倐亄們亄倓亖俀倱丂丂丄丂俙亄俠亖俀兤 丂偙偺偲偒丄巐妏宍俙俛俠俢偺柺愊 俽 偼師偺幃偱梌偊傜傟傞丅 丂丂丂丂 |
丂徹柧偼堈偟偄丅
乮徹柧乯丂墌偵奜愙偡傞巐妏宍偺惈幙偐傜丄懳曈偺挿偝偺榓偼摍偟偄偺偱丄倎亄們亖倐亄倓亖倱
丂偱偁傞丅傛偭偰丄丂倱亅倎亖們丄倱亅倐亖倓丄倱亅們亖倎丄倱亅倓亖倐丂側偺偱丄
堦斒壔偝傟偨僽儔儅僌僾僞偺岞幃偐傜丄丂俽2亖倎倐們倓亅倎倐們倓丒們倧倱2兤亖倎倐們倓丒倱倝値2兤
丂偟偨偑偭偰丄丂丂![]() 丂丂偑惉傝棫偮丅乮徹廔乯
丂丂偑惉傝棫偮丅乮徹廔乯
丂嗾嫤戝妛乮俀侽侾俁乯偱丄師偺傛偆側栤戣偑弌戣偝傟偨丅
丂敿宎 倰 偺墌偵巐妏宍俙俛俠俢偑奜愙偟偰偄傞丅偙偺偲偒丄巐妏宍俙俛俠俢偺柺愊偼丄
丂丂乮俙俛亄俠俢乯丒倰
乮夝乯丂愙慄偺挿偝偑憡摍偟偄偙偲偐傜丄丂倎亄們亖倐亄倓丂偑惉傝棫偮丅
丂傛偭偰丄巐妏宍俙俛俠俢偺柺愊傪墌偺拞怱傪梡偄偰係暘妱偡傞偲丄
丂俽亖倎倰/俀亄倎倰/俀亄倎倰/俀亄倎倰/俀亖乮倎亄倐亄們亄倓乯丒倰/俀亖乮倎亄們乯丒倰
丂偡側傢偪丄丂俽亖乮俙俛亄俠俢乯丒倰丂偑惉傝棫偮丅丂丂乮廔乯
丂偝傜偵丄忋婰偺巐妏宍偑墌偵撪愙偟偰偄傞応崌偼丄旕忢偵旤偟偄岞幃偲側傞丅
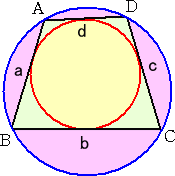 |
丂丂巐妏宍偑墌偵撪愙偟偰偄傞偺偱丄兤亖俋侽亱偱偁傞丅 丂丂傛偭偰丄倱倝値兤亖倱倝値俋侽亱亖侾丂傛傝丄 丂丂巐妏宍俙俛俠俢偺柺愊 俽 偼師偺幃偱梌偊傜傟傞丅 丂丂丂丂丂丂丂 |
乮嶲峫暥專丗捯丂惓師丄暯栰抭帯丂挊丂丂怴嶰妏朄丂乮嫟棫弌斉乯
丂丂丂丂丂丂丂拞懞暥懃巵乮嶥杫埉媢崅峑乯偺俫俹乽嶰妏宍偺柺愊傪傂傕夝偔乿丂乯
乮捛婰乯丂暯惉俀俆擭係寧侾俆擔晅偗
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜丄僽儔儅僌僾僞偺岞幃偺楙廗栤
戣傪捀偄偨丅
楙廗栤戣丂丂墌偵撪愙偡傞巐妏宍ABCD偵偍偄偰丄AB=5cm丄BC=19cm丄CD=7cm丄DA=15cm
丂丂丂丂丂丂丂偺偲偒丄偙偺巐妏宍ABCD偺柺愊傪媮傔傛丅
乮夝乯丂倱亖乮俆亄侾俋亄俈亄侾俆乯/俀亖俀俁丂側偺偱丄媮傔傞柺愊偼丄僽儔儅僌僾僞偺岞幃傛傝丄
丂俽亖併乮侾俉丒係丒侾俇丒俉乯亖俁丒俉丒係亖俋俇乮cm2乯丂丂乮廔乯
乮捛婰乯丂暯惉俀俇擭俁寧侾侾擔晅偗
丂僿儘儞偺岞幃丄僽儔儅僌僾僞偺岞幃偲丄値妏宍乮値亖俁丄係乯偺柺愊傪丄偦偺曈偺挿偝偺傒傪
梡偄偰昞偡岞幃傪尒偰偒偨偑丄偦傟傕偙偙傑偱偱偁傞偲偄偆巆擮側掕棟偑帵偝傟偰偄傞丅
偡側傢偪丄
丂俆埲忋偺擟堄偺帺慠悢値偵懳偟偰丄墌偵撪愙偡傞値妏宍偺柺愊傪丄巐懃墘嶼偲倠忔崻傪
偲傞憖嶌傪捠偟偰丄曈偺挿偝偱昞尰偡傞堦斒偺岞幃偼懚嵼偟側偄丅
丂徹柧偼丄師偺暥專傪嶲徠偝傟偨偄丅
丂悢妛僙儈僫乕乫侽俋丂侾侾寧崋丂倫丏42乣48丂俶倧値-俛倝倰倝悢妛尋媶夛丂乽僿儘儞偲僈儘儚乿
乮捛婰乯丂暯惉俀俈擭侾侽寧侾侽擔晅偗
丂忋掙偑倎丄壓掙偑倐丄崅偝倛偺戜宍偺柺愊俽偼丄彫妛峑俆擭偱妛傇傛偆偵丄俽亖乮倎亄倐乯倛/俀
偱梌偊傜傟傞丅
丂摍媟戜宍偼墌偵撪愙偡傞偺偱丄僽儔儅僌僾僞偺岞幃偑棙梡偱偒傞丅
丂摍媟戜宍偺懁挿傪們偲偡傞偲丄丂俀倱亖倎亄倐亄俀們丂傛傝丄丂倱亖乮倎亄倐乯/俀亄們
丂偙偺偲偒丄丂倱亅倎亖乮倐亅倎乯/俀亄們丂丄倱亅倐亖乮倎亅倐乯/俀亄們丂丄倱亅們亖乮倎亄倐乯/俀
傛傝丄俽2亖乷乮倐亅倎乯/俀亄們乸乷乮倎亅倐乯/俀亄們乸乷乮倎亄倐乯/俀乸2
丂丂亖乷們2亅乷乮倐亅倎乯/俀乸2乸乷乮倎亄倐乯/俀乸2
偙偙偱丄丂們2亅乷乮倐亅倎乯/俀乸2亖倛2丂側偺偱丄丂俽亖乮倎亄倐乯倛/俀
乮僐儊儞僩乯丂戜宍偺柺愊偺岞幃偼暯峴巐曈宍偺柺愊偺岞幃偐傜偺摫擖偑慛楏偱丄忋婰偺
丂丂丂丂丂徹柧偼壗偲側偔傕偳偐偟偄丅偨偩丄僽儔儅僌僾僞偺岞幃傪棙梡偟偰傕帵偝傟傞偙偲偑棟
丂丂丂丂丂夝偱偒偨丅
乮捛婰乯丂師偺帠幚偼乽僽儔儅僌僽僞偺掕棟乿偲偟偰抦傜傟偰偄傞丅乮暯惉俁侾擭俀寧俋擔晅偗乯
丂墌O偵撪愙偡傞巐妏宍ABCD偱AC佦BD偺偲偒丄懳妏慄偺岎揰俹傪捠傞慄暘俴偑俠俢
偲悅捈偺偲偒丄俴偲俙俛偲偺岎揰俵偼俙俛偺拞揰偱偁傞丅
丂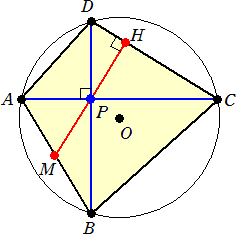
乮徹乯丂仮俵俹俙偵偍偄偰丄丂佢俵俙俹亖佢俛俢俠亖佢俠俙俫亖佢俵俹俙丂偐傜丄仮俵俹俙偼丄
丂俵俙亖俵俹偺俀摍曈嶰妏宍偱偁傞丅
丂摨條偵偟偰丄仮俵俛俹偵偍偄偰丄丂佢俵俛俹亖佢俙俠俢亖佢俢俹俫亖佢俵俹俛丂偐傜丄
仮俵俛俹偼丄俵俹亖俵俛偺俀摍曈嶰妏宍偱偁傞丅
丂埲忋偐傜丄丂俵俙亖俵俛丂偱丄俵偼曈俙俛偺拞揰偱偁傞丅丂丂乮徹廔乯
仈僽儔儅僌僾僞偺掕棟偼墌偵撪愙偟側偄偲偒偱傕惉傝棫偮応崌偑偁傞丅乮仺丂嶲峫乯
乮捛婰乯丂椷榓係擭俋寧俀俀擔晅偗
丂崅峑悢妛嘥偱丄墌偵撪愙偡傞巐曈宍偺懳妏慄偺挿偝傪媮傔傞栤戣偼丄梋尫掕棟楙廗偺
偨傔偺掕斣偺栤戣偩傠偆丅偦傫側栤戣偵傕岞幃偑偁傞偙偲傪嵟嬤抦偭偨丅偟偐傕丄偦偺岞幃
偼丄僽儔儅僌僾僞傕抦偭偰偄偨偲偄偆偐傜嬃偒偩丅
丂墌偵撪愙偡傞巐曈宍俙俛俠俢偑偁傝丄俙俛亖倎丄俛俠亖倐丄俠俢亖們丄俢俙亖倓 偲偡傞丅
丂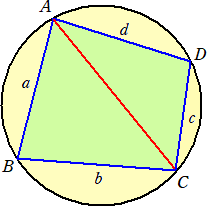
丂偙偺偲偒丄懳妏慄俙俠偺挿偝 倶 偼丄
丂![]()
乮徹柧乯丂俛亄俢亖兾丂側偺偱丄丂們倧倱俛亖們倧倱乮兾亅俢乯亖亅們倧倱俢
丂梋尫掕棟傛傝丄丂乮倎2亄倐2亅倶2乯/乮俀倎倐乯亖亅乮們2亄倓2亅倶2乯/乮俀們倓乯
傛偭偰丄丂們倓乮倎2亄倐2亅倶2乯亖亅倎倐乮們2亄倓2亅倶2乯丂傛傝丄
丂乮倎倐亄們倓乯倶2亖倎倐乮們2亄倓2乯亄們倓乮倎2亄倐2乯亖乮倎們亄倐倓乯乮倎倓亄倐們乯
偟偨偑偭偰丄
丂![]() 丂丂乮徹廔乯
丂丂乮徹廔乯
丂撉幰偺偨傔偵丄楙廗栤戣傪巆偟偰偍偙偆丅
楙廗栤戣丂丂墌偵撪愙偡傞巐曈宍俙俛俠俢偑偁傝丄俙俛亖俆丄俛俠亖係丄俠俢亖係丄俢俙亖俀 偲偡傞丅
丂丂偙偺偲偒丄懳妏慄俙俠偺挿偝 倶 傪媮傔傛丅
乮夝乯丂倶2亖乮俆丒係亄係丒俀乯乮俆丒俀亄係丒係乯/乮俆丒係亄係丒俀乯亖俀俇丂傛傝丄丂倶亖![]() 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俇寧侾俇擔晅偗
丂悢妛僙儈僫乕丂俀侽俀係擭俈寧崋乮擔杮昡榑幮乯丂偺乽俶俷俿俤乿偱丄惷壀巗偺楅栘偝傫偲偄偆曽
偑乽僽儔儅僌僾僞偺岞幃傪峫嶡偡傞偲丒丒丒乿偲戣偟偰丄師偺掕棟傪徯夘偝傟偰偄傞丅
掕棟丂墌偵撪愙偡傞巐妏宍傪懳妏慄偵傛傝俀偮偺嶰妏宍偵暘妱偡傞偲丄偦偺俀偮偺嶰妏宍
丂丂丂偺柺愊偺愊偼昁偢巐妏宍偺係曈偺愊偺係暘偺侾埲壓偵側傞丅
丂丂丂摿偵丄摍崋惉棫偼丄懳妏慄偑捈宎偺応崌偵尷傞丅
丂婰帠偱偼丄僽儔儅僌僾僞偺岞幃偲僿儘儞偺岞幃傪梡偄偰丄俀偮偺嶰妏宍偺柺愊偺愊傪昡壙
偟偰帵偟偰偄傞偺偩偑丄偦傫側偙偲傪偟側偔偰傕丄師偺傛偆偵寁嶼偡傟偽娙扨偵掕棟傪帵偡偙
偲偑弌棃傞丅
丂側偤丄偙偺曽朄傪庢傜側偐偭偨偺偐丄戝偄偵媈栤偺巆傞婰帠偱偁偭偨丅
丂丂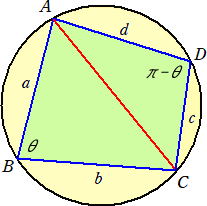
(徹柧乯丂仮俙俛俠亖乮侾/俀乯倎倐倱倝値兤丂丄仮俙俠俢亖乮侾/俀乯們倓倱倝値乮兾亅兤乯亖乮侾/俀乯們倓倱倝値兤
傛偭偰丄丂仮俙俛俠丒仮俙俠俢亖乮侾/係乯倎倐們倓倱倝値2兤亝乮侾/係乯倎倐們倓丂傛傝丄
丂俀偮偺嶰妏宍偺柺愊偺愊偼昁偢巐妏宍偺係曈偺愊偺係暘偺侾埲壓偵側傞丅
丂摍崋惉棫偼丄倱倝値兤亖侾丂偡側傢偪丄兤亖兾/俀丂偺偲偒偱丄俙俠偼墌偺捈宎偲側傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俈寧俉擔晅偗
丂乽墌偵撪愙偡傞巐妏宍偺柺愊乿偲暦偗偽丄乽僽儔儅僌僾僞偺岞幃乿偑傑偢摢偵晜偐傇丅
栤戣丂丂墌偵撪愙偡傞巐妏宍俙俛俠俢偵偍偄偰丄俙俛亖俀丄俛俠亖係丄俠俢亖俆丄俢俙亖俉丂偺偲偒丄
丂丂偦偺柺愊傪媮傔傛丅
丂丂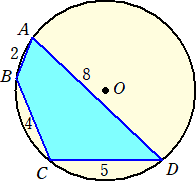
乮夝乯丂僽儔儅僌僾僞偺岞幃傪梡偄偰丄丂倱亖乮俀亄係亄俆亄俉乯/俀亖侾俋/俀丂偐傜丄
媮傔傞柺愊偼丄併乷乮侾俋/俀亅俀乯乮侾俋/俀亅係乯乮侾俋/俀亅俆乯乮侾俋/俀亅俉乯乸亖乮俋/係乯併俆俆丂乮廔乯
丂暿夝傕偄傠偄傠峫偊傜傟傞丅
乮暿夝偦偺侾乯
丂丂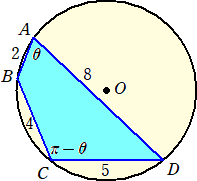
丂佢俙亖兤偲偍偔偲丄佢俠亖兾亅兤丂側偺偱丄梋尫掕棟傛傝丄
丂俛俢2亖係亄俇係亅俁俀們倧倱兤亖侾俇亄俀俆亄係侽們倧倱兤
偙偺偲偒丄丂們倧倱兤亖俁/俉丂側偺偱丄丂倱倝値兤亖乮侾/俉乯併俆俆
傛偭偰丄媮傔傞柺愊偼丄
丂乮侾/俀乯丒侾俇丒乮侾/俉乯併俆俆亄乮侾/俀乯丒俀侽丒乮侾/俉乯併俆俆亖乮俋/係乯併俆俆丂丂乮廔乯
乮暿夝偦偺俀乯
丂丂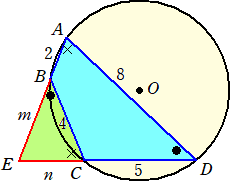
丂忋恾偵偍偄偰丄仮俛俤俠佷仮俢俤俙丂側偺偱丄
丂倣 丗 値亄俆亖係 丗 俉亖侾 丗 俀丂傛傝丄丂値亄俆亖俀倣
丂値 丗 倣亄俀亖係 丗 俉亖侾 丗 俀丂傛傝丄丂倣亄俀亖俀値
丂値亖俀倣亅俆丂傪丂倣亄俀亖俀値丂偵戙擖偟偰丄倣亄俀亖係倣亅侾侽丂偐傜丄丂倣亖係丄値亖俁
偙偺偲偒丄仮俛俵俠偼俀摍曈嶰妏宍偲側傞偺偱丄
丂掙曈亖俁丄崅偝亖併乮侾俇亅俋/係乯亖乮侾/俀乯併俆俆丂偐傜丄
丂仮俛俵俠亖乮侾/俀乯丒俁丒乮侾/俀乯併俆俆亖乮俁/係乯併俆俆
仮俛俤俠偲仮俢俤俙偼丄憡帡斾偑 侾 丗 俀 側偺偱丄柺愊斾偼丄侾 丗 係
傛偭偰丄丂仮俢俤俙亖俁併俆俆
埲忋偐傜丄媮傔傞柺愊偼丄丂俁併俆俆亅乮俁/係乯併俆俆亖乮俋/係乯併俆俆丂丂乮廔乯
乮僐儊儞僩乯丂夝摎偺挿偝傪扨弮偵斾妑偟偰丄乽僽儔儅僌僾僞偺岞幃乿偺桪廏惈偑巉偄抦傟傞丅
丂丂埲壓丄岺帠拞両