
左下の△ABCにおいて、辺BAの延長線上に∠ACP=30°であるように点Pをとり、さら
に、辺CAの延長線上に∠ABQ=20°であるように点Qをとる。
2点P、Qを結び、右下図の四角形を得る。
角の大きさ(2) 
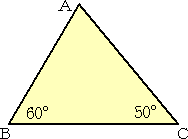
左下の△ABCにおいて、辺BAの延長線上に∠ACP=30°であるように点Pをとり、さら
に、辺CAの延長線上に∠ABQ=20°であるように点Qをとる。
2点P、Qを結び、右下図の四角形を得る。
 |
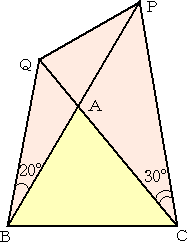 |
このとき、∠CPQは何度になるであろうか?
(答) この問題は、ラングレーの問題と言われ、中学校数学の有名な難問として知られてい
る。答えは、70度である。
実際に、左下図のように、辺CP上に∠CBR=20°であるように点Rをとると、
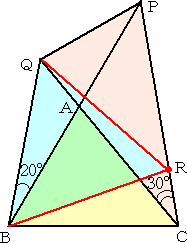 |
△BCQにおいて、∠BCQ=50°で∠QBC=80°から ∠BQC=50°となり、△BCQは、BC=BQの2等辺三 角形となる。また、△BCRにおいて、∠CBR=20°で、 ∠BCR=80°から、∠BRC=80°となり、△BCRは、 BC=BR の2等辺三角形となる。よって、BR=BQ で、 ∠RBQ=60°より、△QBRは正三角形である。 また、∠PBR=∠BPR=40°より、△RPBは2等辺三 |
角形で、RB=RP すなわち、RQ=RP となり、△RPQは2等辺三角形となる。 このとき、∠PRQ=180°−80°−60°=40°なので、∠CPQ=70°となる。 |
|
(コメント) 点Rをとって、正三角形QBRを作るという発想も面白いですが、巧妙に仕組まれ
た角度の設定に感動しますね!
(追記) 平成20年7月29日付け
上記計算の途中結果から、∠BPR=40°なので、∠BPQ=30°であることが分かる。
また、∠BPR=40°ということを用いなくとも、点Rが、BR=PR=QRから、△BPQの
外心で、△QBRが正三角形であることから、∠BPQ=(1/2)∠BRQ=30°であることは
一目瞭然だろう。
#∠BPQの大きさを問う問題が、公庄庸三先生から頂いた「清風高校数学オリンピック」
の問題に取り上げられている。そこでは、上記の証明とは異なる方法で証明されている
ので紹介したい。
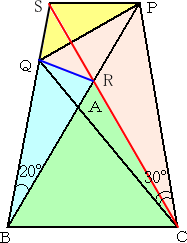 |
左図のような等脚台形BCPSを作り、2点S、Cを結ぶ線分 とBPとの交点をRとおく。 このとき、△BCRは正三角形となる。 また、△BCQは2等辺三角形で、BC=BQ である。 よって、BQ=BRから、△BQRは2等辺三角形で、 ∠BRQ=80°となるので、 ∠PRQ=100° また、 △PRSは正三角形なので、∠PRS=60° |
| よって、 ∠SRQ=40°となる。 また、∠RSQ=40°であるので、△SQRは2等辺三角形となり、 QS=QR SP=RP 、 PQは共通なので、 △PSQ≡△PRQ となる。 よって、∠RPS=60°を線分PQは2等分するので、 ∠BPQ=30°となる。(証終) |
|
(コメント) この証明も、ポイントは正三角形を上手く作るところですね!
∠BPQ=30°が分かれば、∠BPC=40°なので、∠CPQ=70°は明らかとなる。
よおすけさんからのコメントです。(令和2年4月5日付け)
上記の四角形は、以下のサイトの凸四角形と合同です。
月刊「理系への数学」 幾何大王からの挑戦状・特別付録 2012年3月公開(現代数学社)
「ラングレーの問題の初等幾何による証明12選+α」
平成20年7月29日時点では、2通りありますが、上記のサイトを参考に解けば、まだ解法
があるかもしれません。
(追記) 令和5年9月6日付け
上記のラングレーの問題を別な視点から考察してみよう。
ラングレーの三角形を、円内に埋め込んで考える。すなわち、
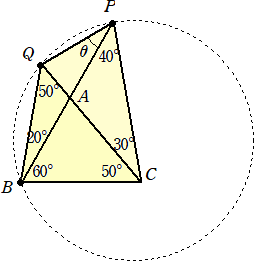
そこで、円周を18等分して、次の図のようにしてみる。
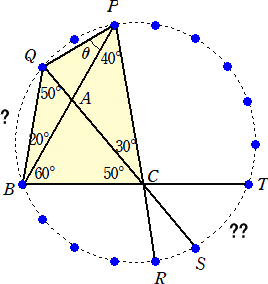
1目盛り当たり(青点間)の円周角の大きさは、 360°÷18÷2=10° なので、例え
ば、∠PBQ=20°なので、弧PQは2目盛り分に相当する。同様に考えて、
弧BRは4目盛り分 、弧RSは1目盛り分 、弧PTは6目盛り分 に相当する。
いくつ分の目盛りに相当するのか、弧BQと弧STについては、問題の条件からは不明で
ある。
ラングレーの問題は、弧BQが3目盛り分に相当することを示す。
分かっている条件は、「?+??=5目盛り分」である。可能性として、
(?,??)=(1,4)、(2,3)、(3,2)、(4,1) の4通りが考えられる。
しかし、(?,??)=(1,4)、(2,3)、(3,2)、(4,1) のとき、3つの線分PR、BT、QS
が1点で交わらず、ラングレーの図形は出来ない。ラングレーの図形が出来るのは、
(?,??)=(3,2) のときのみである。すなわち、
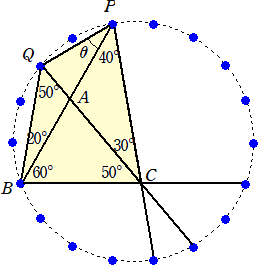
したがって、上図から、θ=30° であることが分かる。
以下、工事中!