
レギオモンタヌス(1436〜1476)は、ドイツの天文学者・数学者である。本名は、ヨハネス・
ミュラー。太陰距離法を導出し、遠洋航海上での経度決定を可能にした。ハレー彗星を観
測し、初めて天体と認定したのも彼である。
高い建物の窓を見るには、どの位置が最も好ましいかを見つけるために、彼は、次のよ
うな問題(1471年)を考えた。
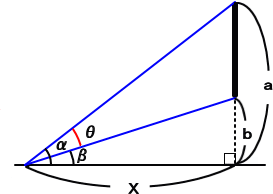
左図において、窓(または絵)を見込む角θ
が最大となる x の値を求めよ。
(解)
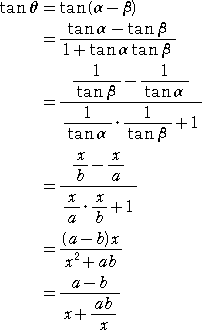
レギオモンタヌスの問題 
レギオモンタヌス(1436〜1476)は、ドイツの天文学者・数学者である。本名は、ヨハネス・
ミュラー。太陰距離法を導出し、遠洋航海上での経度決定を可能にした。ハレー彗星を観
測し、初めて天体と認定したのも彼である。
高い建物の窓を見るには、どの位置が最も好ましいかを見つけるために、彼は、次のよ
うな問題(1471年)を考えた。

左図において、窓(または絵)を見込む角θ
が最大となる x の値を求めよ。
(解)
x は正の数なので、相加平均と相乗平均との関係より、
![]()
したがって、x=ab/x すなわち、![]() のとき、x+ab/x は最小となる。
のとき、x+ab/x は最小となる。
0°<θ< 90°の範囲で、tanθ は単調に増加する関数なので、![]() のとき、
のとき、
tanθ すなわち、θ は、最大となる。 (終)
(追記) 平成29年5月22日付けで、S(H)さんから、tan を用いずに内積で解いてほしい
との要請があったので考えてみた。
(解) 2つのベクトル u=(x,a)、v=(x,b)について、そのなす角をθとすると、
cosθ=u・v/(|u||v|) より、 cos2θ=(u・v)2/(|u|2|v|2)
すなわち、 cos2θ=(x2+ab)2/{(x2+a2)(x2+b2)}
ここで、F(x)=(x2+ab)2/{(x2+a2)(x2+b2)} とおくと、
F’(x)=2(a−b)2x(x2+ab)(x2−ab)/{(x2+a2)(x2+b2)}2
なので、 ![]() のとき、F(x)は極小かつ最小となる。
のとき、F(x)は極小かつ最小となる。
よって、 ![]() のとき、cosθ すなわち、θ は、最大となる。 (終)
のとき、cosθ すなわち、θ は、最大となる。 (終)
以上の計算で、求める x は、a、b の相乗平均になるというところに興味が引かれる。
このことを、実生活に応用してみよう。
私自身、絵が好きで、よく美術館に出かけるが、今まで近くに寄ってみることが多かった。
例えば、身長2m(実際は、これほどないヨ!)の私が、床下から3mのところに額縁の底
辺があり、額縁の高さが 3mの絵をみる場合、どこに立ってみれば一番絵を広くみることが
できるかというと、上の計算から、
x=√{(3+2)(6+2)}=2![]() =2×3.1622=6.3244
=2×3.1622=6.3244
となり、およそ6m半位離れて立てばよいということになる。
(参考文献:大日本百科辞典(小学館)
エリ・マオール 著 好田順治 訳 素晴らしい三角法の世界(青土社))
(追記) X2=ab という式を見ると、下図のような直角三角形が直ぐ思い描かれる。
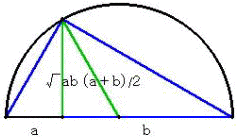
さらに、方べきの定理という見方をすると、長さ x を求めて、下図のような円が容易に作
図できる。(2定点を通り、ある直線に接する円の作図)
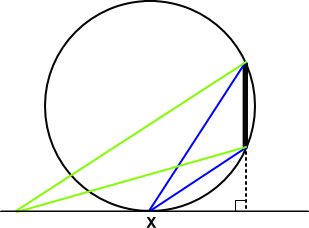
上図から、x の地点で、絵を見込む角が最大になることが理解できる。
(参考) 見込む角についての関連話題 → 「あなたの視力は?」
(追記) 平成29年5月21日付け
1979年度入試から始まった共通一次試験も1990年度入試から大学入試センター試験
と改称され、今また2020年度からは「大学入学共通テスト」(仮称)が受験生に課される予
定である。
その目玉は、記述式試験の採用である。一つの大学内では記述式問題もありだと思うが、
全国共通試験で「記述式」は普通あり得ないと思うのが率直な感想である。
理念的に「記述式」によって思考力や理解力を見たいという気持ちは理解できるが、その
採点を考えた場合、思った以上に大変であり、採点基準を全国共通にすることなど簡単に
口にする以上に難しい問題だと思う。なぜなら、受験生は出題者が意図したようには解答し
ないということである。種々の解答の変化球が採点者を悩ませることになるだろう。
ただ、一度経験してみるといい。「試験に記述式問題を!」という声は、トーンダウンせざる
を得ないことを確信するだろう。
5月17日(水)付け朝日新聞朝刊に、「センター試験後継 記述式の問題例」と題して、国
語と数学の問題例が例示された。数学の問題は、まさにこのページの「レギオモンタヌスの
問題」と同趣旨のもので、大いに興味と関心が引かれた。
東京近郊の大学1年生に解いてもらったところ、正答率は、数学だけで見ても、9.6%〜
59.2%と幅広く、問題の難易度の調整が今後の課題となろう。
さらに、記述試験の特徴として、自己採点結果と実際の結果に大きな開きがあり、自己採
点の難しさがあらためて露呈された形となった。
記述式問題を本当に導入する気があれば、これらの諸問題をあと2〜3年で解決しなけれ
ばならず、ほぼ不可能ではないだろうかと危惧する。無理に強行して、いたずらに受験生を
惑わせることだけはやめて欲しいものだ。
≪数学の問題例≫ ・・・ 長文だったので、問題の趣旨を要約する形で改題させていただきました。
花子さんと太郎さんが、銅像を設置する広場の大きさ、銅像と台座の高さについて検討し
ています。(問題文には、三角比の表(省略)も与えられている。)
(1) 銅像の真正面に立ち、銅像の真下から12m離れた位置から高さ1.5mの台座に乗
せた高さ4mの銅像を見る。このとき、目の高さが1.5mの花子さんの銅像を見込む角
として最も近いものを一つ選べ。
(選択肢) 4°6°8°10°12°14°16°18°20°22°
(2) 銅像ABを台座から離れた地点Pで見たときの見込む角について、太郎さんは次のよ
うに考えた。
【太郎さんの考え】
3点A、B、Pを通る円の半径をRとすると、ABの長さは常に一定であることから、∠APB
が鋭角ならば、∠APBが最大となるのは、Rが最小のときである。
(イ) ∠APBが鋭角であることを確かめる方法を、△APBの3辺の長さAB、AP、BPにつ
いての式を用いて説明せよ。
(ロ) 【太郎さんの考え】が正しいことは、sin∠APB、AB、Rを用いたある関係式と、
「∠APBが鋭角のとき、∠APBが大きくなるほどsin∠APBの値は大きくなる」
ことから分かる。その関係式を答えよ。
(ハ) 2人は【太郎さんの考え】について先生に相談したところ、Rが最小になるのは、3点
A、B、Pを含む平面上において、3点A、B、Pを通る円と点Pを通り直線ABに垂直な直
線が接するときであることを教えてもらった。
この考えに基づくと、目の高さが1.5mの花子さんが、高さ6.5mの台座の上に乗せた
高さ4mの銅像を見る場合、3点A、B、Pを通る円の半径Rが最小となるのはいつか。また、
このときの見込む角として最も近いものを一つ選べ。
(選択肢) 11°13°15°17°19°21°23°25°27°29°
(3) このときの銅像の真下からの距離はおよそいくらか。最も適当なものを一つ選べ。
(選択肢) 3.7 4.7 5.7 6.7 7.7 8.7 9.7 10.7 11.7 12.7
(正答例)(1) 18° (2)(イ) AP2+BP2>AB2 を確かめる。
(ロ) sin∠APB=AB/(2R) (ハ) R=7 、17° (3) 6.7m
(正答率)(1) 59.2% (2)(イ) 24.2% (ロ) 35.8% (ハ) R:9.6% 、15.4% (3) 18.6%