
中学・高校で学ぶ確率の計算では、
全体で n 通りの場合があり、そのいずれも同様に確からしいとする。
ある事柄Aが r 通りの方法で出現するとき、Aが起こる確率は、r/n
をもとに計算される。(→ 参考:「幾何学的確率」)
この定義では、「n 通り」とあるので、起こりうる場合の数は有限集合が前提になっている。
ところが、起こりうる場合の数が無限集合でも、確率の計算をすることができる場合がある。
例 自然数を1つ選ぶとき、それが3の倍数である確率が、1/3であることは自然に受け入
れ可能だろう。
1、2、3、4、5、6、・・・ と3つおきに3の倍数が表れるので、3個中1個というLaplace流
の考え方が自然に拡張されるからだと思われる。
上記の例では、「3つおきに3の倍数が表れる」ことから確率1/3としたが、もう少しきちん
と整理してみよう。
自然数 1、2、3、・・・、N のうちで、3の倍数の個数は、ガウスの記号[ ]を用いて [N/3]
で与えられる。
[N/3] は、Nを3で割った商なので、Nを3で割った余りを R とおくと、
N=3・[N/3]+R (0≦R<3)
が成り立つ。 よって、 [N/3]/N=1/3−R/(3N) である。
このとき、 N → ∞ とすると、 [N/3]/N → 1/3 となる。
もう少し、いくつかの具体例を見てみよう。
例 自然数を1つ選ぶとき、それが4と互いに素である確率を求めよ。
連続した4個の自然数のうちの一つは4で割り切れ、他の数は4で割ると余りが、1、2、
3 の何れかとなる。したがって、連続した4個の自然数のうちには4と互いに素であるもの
が2個ある。よって、求める確率は、2/4=1/2 である。
例 自然数を1つ選ぶとき、その平方数の一の位が1である確率を求めよ。
連続した10個の自然数のうち、平方数の一の位が1であるのは、元の数の一の位が1
または9である場合である。よって、求める確率は、2/10=1/5 である。
例 自然数を1つ選ぶとき、その10乗した数の一の位が6である確率を求めよ。
連続した10個の自然数のうち、10乗した数の一の位が6であるのは、元の数の一の位
が4または6である場合である。よって、求める確率は、2/10=1/5 である。
例 4より大きい自然数を1つ選ぶとき、nC4が4で割り切れる確率を求めよ。
nC4=n(n−1)(n−2)(n−3)/4!より、nC4が4で割り切れるためには、
n(n−1)(n−2)(n−3)が42=16で割り切れればよい。
すなわち、nを16で割ったとき、余りが0、1、2、3になれば、n(n−1)(n−2)(n−3)は
16で割り切れる。連続する16個の自然数のうち、4個の自然数がこの条件を満たす。
よって、求める確率は、4/16=1/4 である。
例 自然数 n を1つ選ぶとき、2n の一の位が2である確率を求めよ。
例 自然数 n を1つ選ぶとき、2n の先頭が2で始まる確率を求めよ。
例 2つ選んだ自然数が互いに素である確率を求めよ。(答え:6/π2)
例 4つ選んだ自然数が1以外の公約数を持つ確率を求めよ。(答え:1−90/π4)
上記では、起こりうる場合の数が無限集合の場合を考えたが、線分上の点の集合や平面
図形などの連続変量でも同様に確率らしきものを考えることは可能である。
いくつかの具体例を見てみよう。
例 長さ 4 cmの木の棒が途中で折れた。このとき、短い方の棒の長さが 1cmより大きい
確率を求めよ。
長さ 4 cmの木の棒ABの中点Oを共有する長さ2の線分MNを考える。
短い方の棒の長さが 1 cmより大きくなるためには、線分MNの間で折れればよい。
よって、求める確率は、 2/4=1/2 である。
例 1辺の長さが10cmの正方形を床に敷き詰める。床の上から、直径2cmの硬貨を落と
すとき、硬貨が正方形のどの辺とも交わらない確率を求めよ。
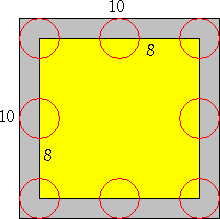
1つの正方形で考える。硬貨が正方形のどの辺とも交わらないためには、硬貨の中心が
上図のような1辺の長さが8cmの正方形の内部にあればよい。
よって、求める確率は、 64π/100π=16/25 である。
上記では、もちろん、ある一定の解釈のもとに確率を計算している。解釈によって、異なる
確率が得られる場合がある。そのような例としては、Bertrandの逆説が有名であろう。
Bertrandの逆説(Bertrand著「確率論」(1889年)で作例。命名はポアンカレによる)
与えられた円Oに任意に1本の弦Lを引くとき、この弦の長さが内接正三角形ABCの
1辺の長さより大きくなる確率を求めよ。
この問題に対して、「同様に確からしい」ということの解釈によっては、いろいろな確率の
値の可能性があることを、Bertrandは指摘した。
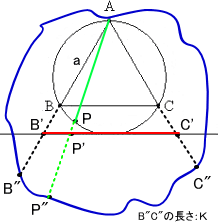
(case 1) L>a ⇔ Pが劣弧BC上
このとき、確率=1/3
(case 2) L>a ⇔ P’が線分B’C’上
このとき、確率=0
(case 3) L>a ⇔ P”が部分曲線B”C”上
このとき、確率=K/閉曲線の全長
(case 4) L>a ⇔ 弦の中点が三角形ABCの内接円
の内部
このとき、確率=1/4
(case 5) L>a ⇔ 弦BCと、弦BCのOに関して点対
称な弦の両弦にはさまれる
このとき、確率=1/2
この例のように、有限個を前提としたLaplace流の確率を無限個の場合にそのまま形式
的に拡張するときは注意を要する。
Bertrandの逆説の場合、無作為に与えるものが何であるかが問題では不明確であるた
め、いろいろな確率の値が存在したのである。
因みに、この問題をコンピュータを用いて実験的に求めると、0.371となるらしい。この
数字は、1/2、1/3、1/4の平均0.361・・・に近い。何やら意味深ですね!
以下、工事中