
偶然現象を考察する数学的理論で、同一分布のもとで不変な性質を調べるのが、確率論
の目的である。我々の生活している社会には、確率を使って初めてとらえることのできる現
象というものがたくさんある。
例えば、降水確率、人口統計、各種保険の保険料や年金の計算、商品の販売計画、建
造物の設計など、確率論が必要とされる分野は多様である。
個人の感覚、経験に頼っていたものが数値化され、将来を予測し、人を説得し、社会を動
かす道具となり得る。その意味では、一番人間にとって身近な数学といえる。
このページでは、古典的な確率論をもとに幾何学的確率の問題を考察してみようと思う。
中学・高校で学ぶ確率は、Laplaceによって与えられた次の定義がもとになっている。
Laplaceの算術的確率(Laplace著「確率の解析的理論」(1812年)による)
全体で n 通りの場合があり、そのいずれも同様に確からしいとする。ある事柄Aが
r 通り
の方法で出現するとき、Aの確率は、r/n と定める。
この定義で最大の難所は「同様に確からしい」という文言であろう。確率を定義するのに、
確率を用いているという批判は避けられない。これに対して、ラプラスは次のように述べて
いる。
我々が無知ゆえに確率ということが問題になるのであって、同様に確からしいということ
は、それを判断する知識が欠けているということを意味する。例えば、硬貨を投げたとき、
表が出るのと裏が出るのと、どちらがより確からしいか全く分からない。そこで、表が出る
ことと裏が出ることは、同様に確からしい、とするのである。
19世紀になって、古典的確率論が対象としたものとは全く別の方面に属する問題に、確
率の考えや計算手法が適用され、その有効性が確認された。
例えば、現在20歳の人が50年後生存しているかどうかという問題は、生存・非生存とい
う、2つの結果を持ったゲームの繰り返しと考えられる。ところが、統計的な経験によれば、
ある事柄の起こる相対度数は次第に一定の値に近づいていくということが知られていた。こ
の値を、20歳の人が50年後生存している確率と呼ぶことは、ごく自然なことである。この新
しい確率に、古典的確率論の言葉や計算を適用し、生命保険の保険料や年金の計算など、
実際的で興味ある多くの結果が得られた。
この新しい確率では、「同様に確からしい」ということを考えることができなくなった。そこで、
これら2つの考え方を統合する新しい定義が必要となった。
R.von Misesの経験的確率(統計的確率)
n個の独立な試行中、ある事柄Aがr回出現したとする。もし、nを十分大きくしたとき、相
対度数 r/n が一定値pに近づくとき、pをAの確率と定義する。
Laplace流の算術的確率の定義を連続変数に拡張しようとする場合、次のBertrandの逆
説は有名である。
Bertrandの逆説(Bertrand著「確率論」(1889年)で作例。命名はポアンカレによる)
与えられた円Oに任意に1本の弦Lを引くとき、この弦の長さが内接正三角形ABCの
1辺の長さより大きくなる確率を求めよ。
この問題に対して、「同様に確からしい」ということの解釈によっては、いろいろな確率の
値の可能性があることを、Bertrandは指摘した。
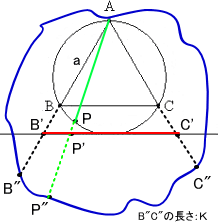 |
(case 1) L>a ⇔ Pが劣弧BC上 このとき、確率=1/3 (case 2) L>a ⇔ P’が線分B’C’上 このとき、確率=0 (case 3) L>a ⇔ P”が部分曲線B”C”上 このとき、確率=K/閉曲線の全長 (case 4) L>a ⇔ 弦の中点が△ABCの内接円の 内部 このとき、確率=1/4 (case 5) L>a ⇔ 弦BCと、弦BCのOに関して 点対称な弦の両弦にはさまれる このとき、確率=1/2 |
この例のように、有限個を前提としたLaplace流の確率を無限個の場合にそのまま形式
的に拡張するときは注意を要する。Bertrandの逆説の場合、無作為に与えるものが何で
あるかが問題では不明確であるため、いろいろな確率の値が存在したのである。
因みに、この問題をコンピュータを用いて実験的に求めると、0.371となるらしい。この
数字は、1/2、1/3、1/4の平均0.361・・・に近い。何やら意味深ですね!
確率を、数学的にあいまいさがない形に定義したのは、A.Kolmogorov
である。
A.Kolmogorovの測変論的確率
(A.Kolmogorov著「確率論の基礎」(1933年)による)
根元事象全体からなる集合を標本空間といい、Ωで表す。
標本空間Ωの部分集合からなる族Fで次の条件を満たすものを、Borel集合体という。
(1) ΩはFに属する。
(2) AがFに属すれば、Aの補集合もFに属する。
(3) AK(K=1,2,3、・・・)がFに属するとき、それらの和集合もFに属する。
この定義から、Borel集合体は、集合の交わり、差集合についても閉じていることが分か
る。このとき、F上で定義された実数値関数P(A)で、次の3条件を満たすものを確率という。
(1) P(A)≧0
(2) P(Ω)=1
(3) Fの要素AK(K=1,2,3、・・・)において、互いに排反(2つの交わりが空集合)のと
き、AK(K=1,2,3、・・・)の和集合に対応する値は、P(AK) (K=1,2,3、・・・)の和
になる。
このようにして定義される(Ω、F、P)を確率空間といい、Pを確率測度という。
また、P(A)≦1、P(φ)=0、P(Aの補集合)=1−P(A) ということも簡単に示すことができる。
Laplace流の確率を、Kolmogorov的に見直せば次のようになる。
数学的模型 正しい硬貨を投げて、表なら1、裏なら0とする。
Ω={0,1} 、F=Ωの部分集合全体 、P(A)=(Aの要素の個数)/2
とおくと、(Ω、F、P)は確率空間をなす。
確率を定義するとき、必ず3点Ω、F、Pがセットになっている。従って、標本空間が同じで
あっても、確率空間が違えば、違う確率となる。
Bertrandの逆説では、これら3点Ω、F、Pが異なるものであるので、異なる確率が出てき
ても何ら不思議はないわけである。
ある集合から1つの要素を取り出すとき、どの要素がとられるか同程度に期待されない場
合もある。その場合、確率密度関数F(X)という実数値関数を考える。
確率密度関数F(X)は次の条件を満たすものとする。
(1) F(X)≧0
(2) 定義域におけるF(X)の定積分=1
このとき、確率P(A)は、AにおけるF(X)の定積分で定義される。
例 一様な密度τを持った長さLの線分ABの質量を1とする。線分AB上から1点を選ぶと
き、線分CD(長さM)上にある確率を求めよ。
まず、τ×L=1なので、τ=1/L。よって、確率密度関数F(X)=1/L
とする。
このとき、線分CD上にある確率=CDにおけるF(X)の定積分=M/L
この例は、幾何学的確率の計算の理論的背景を示唆している。また、次の例も、幾何学
的確率の問題として興味深い。
(これは、職場の同僚Sさんより、忘れていた記憶を思い出させていただいた!)
例(Buffonの針の問題)
平面上に等間隔(ここでは、距離=4とする)で無数の平行線が引いてある。今この平面
に、長さ2の針を落とすとき、その針が平行線と交わる確率を求めよ。
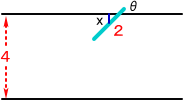
針の中心から最も近い平行線までの距離を x 、針と平行
線のなす角をθとすると、針の位置は、この x と θ で決ま
る。このとき、0≦x≦2で、0≦θ≦π (角度の単位はラジ
アン)である。
針が平行線と交わるための必要十分条件は、x≦sinθ
|
右図の網掛部分の面積は、2なので、 求める確率は、1/π となる。 (Sさんは、π が出てくるところが面白いと仰っていたが、確かに、興味あるところである。) このことから、この実験を何千、何万回と繰り返すことにより、πの近似値が求められそうである。その実験は読者の方にまかせよう。 |
 |
(参考文献:渡部隆一 著 確率(共立出版)
御園生善尚 他著 統計学大要(養賢堂)
風巻紀彦 講義録 確率とその応用)
(追記) G.L.Buffon (1707〜1788) 自然の歴史の研究で著名。
Buffonの針の問題において、机上の理論値(1/π)が、多くの人によって実験的によく当
てはまることが確かめられている。(参考:放課後の数学)
同じような問題:
「空間で同一平面上に間隔hで多くの絃が平行に張られているとき、上から落とした長さL
(L<h)の針がこれらの絃に当たる確率は、L/(2h) である。」
についても、理論値と実験値がよく合うことが確かめられているそうである。
(参考文献:数学100の定理(日本評論社))
(再追記) 平成15年2月15日付朝日新聞夕刊のコラム「藤原正彦の遠めがね虫めがね」
において、Buffonの針の問題の話題が取り上げられている。
実際に針を落とす実験をした人がいて、2000回では、机上の理論値(1/π)との誤差
が、1%強だったという。その後その人は、コンピュータを用いてシミュレーションした結果
試行回数を10倍にする度に、誤差が約0.28倍に縮まることに気づかれたという。理論
的には、1/√10倍(≒0.32)らしい。一定の割合で、机上の理論値(1/π)に近づくとは、
とても律儀な振る舞いだ。藤原先生の文章には、いつも感心させられるが、次の一文に、
特に魅せられた。
「この世のどんな現象にも数学がつまっている。しかも、なぜか美しい。」
当HPがいつもお世話になっているHN「GAI」さんからのコメントです。
(平成25年12月20日付け)
平行線の間隔がDで、針の長さをLとするとき、針が平行線と交わる確率Pは、通常 L≦D
で考察されている。(p=2L/πD)
ここでは、L≧D なる針について調べてみた。L/D=k とおく。
k=2![]() /3 (=1.1547・・・) のとき ---> p=(π+2
/3 (=1.1547・・・) のとき ---> p=(π+2![]() )/(3π) (=0.700896・・・)
)/(3π) (=0.700896・・・)
k=![]() (=1.4142・・・)の時 --------> p=(π+4(
(=1.4142・・・)の時 --------> p=(π+4(![]() -1))/(2π) (=0.763696・・・)
-1))/(2π) (=0.763696・・・)
k=2の時 ----------------------> p=(2π+6(2-![]() ))/(3π) (=0.837248・・・)
))/(3π) (=0.837248・・・)
以下、p=1+(2/π)(k(1-√(1-1/k2))-Arcsin(1/k)) で、pは、kについて単調増加となり、
k → ∞ ならば、 p → 1
また、k>π/4 (=0.785398・・・) で、 p>1/2 が起こる。
GAI さんから新しい問題提起です。(平成26年1月20日付け)
一定の幅d1に横に平行に引かれた直線群に一定の幅d2でこれに垂直に引かれた直線群
があり平面に無数の縦d1、横d2の長方形がある。この図形に長さL(L<min{d1,d2} とする)の
針を落下させるとき、針が長方形の周と交わる確率はどんな値になるでしょう?
(追記) 令和3年12月17日付け
上記の「Buffonの針の問題」では、円周率πの近似値を実験的に体感することができた。
これと同様に、ある無理数の近似値を実験的に体感する問題が知られている。
(駐車の問題)
長さLの街路に長さ2の車が縦列駐車をすることを考える。
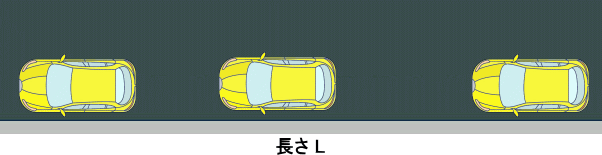
上図では、3台の車が駐車している。車が駐車できるスペースがあれば、どんどん駐車し、
もう駐車するスペースがなくなるまで続けるものとする。
このとき、駐車できた車の台数をT(L)とおく。
自然数Nに対して、T(L)=N となる確率を求める問題が「駐車の問題」である。
ここで、T(L)=N となる確率を、P(L,N)で表すことにする。
例 2≦L≦4 のとき、 P(L,1)=1 、P(L,2)=0
P(6,1)=0 、P(6,2)=1 、P(6,3)=0
上記例と同様にして、P(8,1)=0、P(8,4)=0 は直ぐ分かるが、P(8,2)やP(8,3)
は、どのような値を取るだろうか?直ぐ、P(8,3)=1とは言えないところが心憎い。
今、P(8,2)を求めることを考える。
街路の長さが8なので、閉区間[0,8]で考える。また、車の長さが2で、車の止まる位置を
車の中心に対応させることにする。
このとき、1台目の車が止まりうる範囲は閉区間 I=[1,7]となる。ただし、閉区間[3,5]
の範囲に車が止まると、両側に車の駐車スペースが出来るので、題意に反してしまう。
よって、閉区間[3,5]は除外し、1台目の車が止まりうる範囲は、
I1=[1,3] または I2=[5,7]
の何れかとなる。
今、閉区間 I1=[1,3]を点列 1=x0,x1,・・・,xn=3 によって、n個の小区間に分割し、
その小区間の長さをΔxk (k=0,1,・・・,n−1) とおく。
このとき、1台目が閉区間 I(xk,Δxk)=[xk,xk+Δxk]に駐車する確率は、
{(xk+Δxk)−xk}/(7−1)=Δxk/6
で、2台目が、I− I(xk,Δxk)の範囲に駐車し、残りのスペースに3台目が駐車出来なくす
るためには、閉区間[5,xk+4] の範囲に駐車しなければならない。このとき、起こり得る範
囲は、閉区間[xk+2,7] なので、確率は、
{(xk+4)−5}/{7−(xk+2)}=(xk−1)/(5−xk)
となるので、結果として、求める確率は、
(Δxk/6)×(xk−1)/(5−xk)=(xk−1)/(5−xk)Δxk/6
となる。よって、1台目が I1=[1,3] に駐車する確率は、
Σ(xk−1)/(5−xk)Δxk/6
で、同様に、1台目が I2=[5,7] に駐車する確率は、
Σ(xk−1)/(5−xk)Δxk/6
となるので、求める確率P(8,2)は、
P(8,2)=limΔxk→0 Σ(xk−1)/(5−xk)Δxk/3=∫13 (x−1)/(5−x)dx/3
と表せる。実際に解くと、 P(8,2)=(4log2−2)/3 となる。
このとき、 P(8,3)=1−(4log2−2)/3=(5−4log2)/3 である。
(コメント) 以上の計算から、駐車の問題において、自然対数 log2 の値が実験的に体感
出来ることが分かった。
以下、工事中!