単位分数の和 
単位分数とは、分子=1である分数のことをいう。
古代のエジプトでは、互いに異なる単位分数の和として分数を表した。そこで、このような
表記の仕方は、エジプト分数と言われ、ヨーロッパでは中世まで広く使われたらしい。
例 5/6=1/x+1/y を満たす異なる自然数 x、y を求めよ。
多分計算が得意な方は、「1/2+1/3=5/6」から直ちに、x=2、y=3を見いだすことだ
ろう。
一つの分数 m/n を単位分数の和として表すには、次の手順に従えばよい。
(手順) 1. m/n>1/x を満たす最大の単位分数1/x を見いだす。
2. 新しい分数 m/n−1/x について、1.を行う。この操作を繰り返す。
例 5/6 を超えない最大の単位分数は、1/2で、5/6−1/2=2/6=1/3
よって、5/6=1/2+1/3
例 8/11 を超えない最大の単位分数は、1/2で、8/11−1/2=5/22
5/22 を超えない最大の単位分数は、1/5で、5/22−1/5=3/110
3/110 を超えない最大の単位分数は、1/37で、3/110−1/37=1/4070
以上から、 8/11=1/2+1/5+1/37+1/4070
このような表し方は一意に定まるものではなく、 8/11=1/2+1/6+1/22+1/66 と
いう分解も考えられる。
単位分数をいくらでも使ってよければ必ず一つの分数は単位分数の和として表される。
それに対して、使える単位分数の個数を制限すると、問題は極端に難しくなる。
2以上の全ての自然数 N について、等式
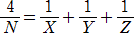
を満たす自然数 X、Y、Z が存在するかどうかは、まだ未解決の問題らしい。
ものの本によると、1億より小さいNの値に対しては、自然数 X、Y、Z は必ず存在する
ことが知られている。
2以上の全ての自然数 N について、等式
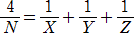
を満たす自然数 X、Y、Z は存在するだろう
というのが、エルデスとシュトラウスの予想である。(→ 参考:「単位分数を作る」)
比較的小さいNの値に対して自然数 X、Y、Z の値を見つけることは、小学校程度の適度
な計算練習と言える。ただ、その計算方法は、日本の学校教育で与えられるものとは違い、
どちらかというと欧米的である。
自分自身の脳の活性化のために、出来るところまで表を完成させようという気になった。興
味ある読者の方もご一緒にいかがだろうか?「エジプト分数で!」という条件を付けると厳し
そうなので、以下の表では同じ分母も可としよう。
| |
| N |
X |
Y |
Z |
|
N |
X |
Y |
Z |
| 2 |
1 |
2 |
2 |
3 |
2 |
2 |
3 |
| 4 |
2 |
4 |
4 |
5 |
2 |
5 |
10 |
| 6 |
3 |
6 |
6 |
7 |
4 |
4 |
14 |
| 8 |
4 |
8 |
8 |
9 |
6 |
6 |
9 |
| 10 |
5 |
10 |
10 |
11 |
6 |
6 |
33 |
| 12 |
6 |
12 |
12 |
13 |
4 |
26 |
52 |
| 14 |
7 |
14 |
14 |
15 |
10 |
10 |
15 |
| 16 |
8 |
16 |
16 |
17 |
6 |
17 |
102 |
| 18 |
9 |
18 |
18 |
19 |
6 |
38 |
57 |
| 20 |
10 |
20 |
20 |
21 |
14 |
14 |
21 |
| 22 |
11 |
22 |
22 |
23 |
12 |
12 |
138 |
| 24 |
12 |
24 |
24 |
25 |
10 |
25 |
50 |
| 26 |
13 |
26 |
26 |
27 |
18 |
18 |
27 |
| 28 |
14 |
28 |
28 |
29 |
8 |
116 |
232 |
| 30 |
15 |
30 |
30 |
31 |
16 |
16 |
248 |
| 32 |
16 |
32 |
32 |
33 |
22 |
22 |
33 |
| 34 |
17 |
34 |
34 |
35 |
14 |
35 |
70 |
| 36 |
18 |
36 |
36 |
37 |
10 |
185 |
370 |
| 38 |
19 |
38 |
38 |
39 |
26 |
26 |
39 |
|
上記の表を埋めていく過程で、Nが偶数ならば、必ず等式を満たす自然数 X、Y、Z
の値
が見つけられることに気がつく。しかし、Nが奇数のときは、とても不規則だ。Nの素因数分
解と密接に結ぶついていて、自然数 X、Y、Z の値が見つけられるかどうか、確信が持てな
い。エルデスとシュトラウスの予想を証明するには、Nが奇数のときを考えればよい。
以下では、Nが奇数の場合のみを考えることにする。
| |
| N |
X |
Y |
Z |
|
N |
X |
Y |
Z |
| 41 |
12 |
123 |
164 |
43 |
12 |
172 |
258 |
| 45 |
30 |
30 |
45 |
47 |
14 |
94 |
329 |
| 49 |
28 |
28 |
98 |
51 |
34 |
34 |
51 |
| 53 |
14 |
371 |
742 |
55 |
22 |
55 |
110 |
| 57 |
38 |
38 |
57 |
59 |
30 |
30 |
885 |
| 61 |
18 |
122 |
549 |
63 |
42 |
42 |
63 |
| 65 |
26 |
65 |
130 |
67 |
18 |
402 |
603 |
| 69 |
46 |
46 |
69 |
71 |
20 |
284 |
355 |
| 73 |
20 |
292 |
730 |
75 |
50 |
50 |
75 |
| 77 |
44 |
44 |
154 |
79 |
21 |
474 |
1106 |
| 81 |
54 |
54 |
81 |
83 |
42 |
42 |
1743 |
| 85 |
30 |
102 |
255 |
87 |
58 |
58 |
87 |
| 89 |
24 |
534 |
712 |
91 |
52 |
52 |
182 |
| 93 |
62 |
62 |
93 |
95 |
38 |
95 |
190 |
| 97 |
28 |
194 |
2716 |
99 |
66 |
66 |
99 |
|
とうとう100まで達成!日本100名山とか、100という数字は縁起がいいので、手計算
による方法はここで打ち切りにすることにしよう。
上記の表からも分かるように、Nの値が素因数分解されるときは比較的平易に自然数 X、
Y、Z の値が見つけられる。それに対して、Nが素数のときは、意外に手強い。
表では、解が一つしか示されていないが、もちろん、解は一つには定まらない。
例えば、次のような別解もある。
| |
| N |
X |
Y |
Z |
|
N |
X |
Y |
Z |
| 4 |
3 |
3 |
3 |
6 |
4 |
4 |
6 |
| 7 |
2 |
28 |
28 |
8 |
6 |
6 |
6 |
| 12 |
9 |
9 |
9 |
16 |
12 |
12 |
12 |
| 19 |
5 |
190 |
190 |
20 |
15 |
15 |
15 |
|
当HPがいつもお世話になっている「らすかる」さんが1000までの素数について調べられ
た。(平成17年11月19日付け)
それをまとめたものが下表である。らすかるさんに感謝します。
| N |
X |
Y |
Z |
|
N |
X |
Y |
Z |
| 101 |
28 |
404 |
707 |
103 |
28 |
412 |
1442 |
| 107 |
30 |
321 |
1070 |
109 |
30 |
545 |
654 |
| 113 |
30 |
678 |
1695 |
127 |
64 |
64 |
4064 |
| 131 |
36 |
524 |
1179 |
137 |
36 |
1233 |
1644 |
| 139 |
36 |
1668 |
2502 |
149 |
38 |
2831 |
5662 |
| 151 |
40 |
1208 |
1510 |
157 |
40 |
3768 |
4710 |
| 163 |
42 |
2282 |
3423 |
167 |
70 |
105 |
7014 |
| 173 |
48 |
519 |
2768 |
179 |
70 |
126 |
8055 |
| 181 |
48 |
1086 |
2896 |
191 |
52 |
764 |
2483 |
| 193 |
50 |
1930 |
4825 |
197 |
50 |
4925 |
9850 |
| 199 |
100 |
100 |
9950 |
211 |
54 |
3798 |
5697 |
| 223 |
60 |
1115 |
2676 |
227 |
60 |
1362 |
4540 |
| 229 |
60 |
2290 |
2748 |
233 |
60 |
3495 |
4660 |
| 239 |
66 |
717 |
5258 |
241 |
66 |
723 |
15906 |
| 251 |
68 |
1004 |
4267 |
257 |
74 |
514 |
9509 |
| 263 |
70 |
1841 |
2630 |
269 |
68 |
9146 |
18292 |
| 271 |
72 |
2168 |
2439 |
277 |
72 |
2493 |
6648 |
| 281 |
76 |
1124 |
5339 |
283 |
78 |
849 |
7358 |
| 293 |
78 |
1758 |
3809 |
307 |
80 |
3070 |
4912 |
| 311 |
80 |
4976 |
6220 |
313 |
80 |
5008 |
12520 |
| 317 |
84 |
2219 |
3804 |
331 |
84 |
9268 |
13902 |
| 337 |
90 |
1685 |
6066 |
347 |
90 |
3123 |
10410 |
| 349 |
90 |
5235 |
6282 |
353 |
90 |
7060 |
12708 |
| 359 |
91 |
10052 |
18668 |
367 |
184 |
184 |
33764 |
| 373 |
96 |
4476 |
11936 |
379 |
96 |
12128 |
18192 |
| 383 |
98 |
5362 |
18767 |
389 |
102 |
2334 |
19839 |
| 397 |
114 |
794 |
22629 |
401 |
108 |
1604 |
10827 |
| 409 |
105 |
5726 |
12270 |
419 |
110 |
4190 |
4609 |
| 421 |
108 |
5052 |
22734 |
431 |
114 |
2586 |
8189 |
| 433 |
112 |
6062 |
6928 |
439 |
112 |
7024 |
24584 |
| 443 |
112 |
18606 |
21264 |
449 |
114 |
8531 |
51186 |
| 457 |
120 |
3656 |
6855 |
461 |
120 |
3688 |
13830 |
| 463 |
120 |
4630 |
11112 |
467 |
120 |
7005 |
11208 |
| 479 |
126 |
3353 |
8622 |
487 |
126 |
4383 |
20454 |
| 491 |
126 |
8838 |
10311 |
499 |
126 |
20958 |
31437 |
| 503 |
132 |
3018 |
22132 |
509 |
146 |
1018 |
37157 |
| 521 |
140 |
2084 |
18235 |
523 |
138 |
3138 |
12029 |
| 541 |
140 |
5410 |
15148 |
547 |
150 |
1641 |
27350 |
| 557 |
144 |
5013 |
26736 |
563 |
144 |
9008 |
20268 |
| 569 |
150 |
3414 |
14225 |
571 |
144 |
27408 |
41112 |
| 577 |
145 |
33466 |
167330 |
587 |
154 |
4109 |
12914 |
| 593 |
150 |
17790 |
44475 |
599 |
156 |
7188 |
7787 |
| 601 |
154 |
6611 |
92554 |
607 |
156 |
7284 |
23673 |
| 613 |
168 |
1839 |
34328 |
617 |
156 |
24063 |
32084 |
| 619 |
160 |
6190 |
19808 |
631 |
160 |
20192 |
25240 |
| 641 |
168 |
4487 |
15384 |
643 |
168 |
5144 |
13503 |
| 647 |
165 |
14234 |
19410 |
653 |
170 |
6530 |
11101 |
| 659 |
168 |
15816 |
18452 |
661 |
174 |
3966 |
19169 |
| 673 |
170 |
22882 |
57205 |
677 |
176 |
7447 |
10832 |
| 683 |
342 |
342 |
116793 |
691 |
180 |
6219 |
13820 |
| 701 |
182 |
9113 |
9814 |
709 |
180 |
21270 |
25524 |
| 719 |
182 |
28041 |
30198 |
727 |
186 |
8724 |
90148 |
| 733 |
192 |
4398 |
46912 |
739 |
189 |
10346 |
39906 |
| 743 |
310 |
465 |
138198 |
751 |
189 |
40554 |
94626 |
| 757 |
192 |
18168 |
48448 |
761 |
198 |
6849 |
16742 |
| 769 |
201 |
4614 |
103046 |
773 |
196 |
21644 |
37877 |
| 787 |
204 |
9444 |
13379 |
797 |
205 |
7970 |
65354 |
| 809 |
210 |
8090 |
16989 |
811 |
210 |
11354 |
12165 |
| 821 |
209 |
18062 |
31198 |
823 |
210 |
17283 |
24690 |
| 827 |
210 |
24810 |
28945 |
829 |
216 |
6632 |
22383 |
| 839 |
336 |
560 |
176190 |
853 |
220 |
8530 |
37532 |
| 857 |
224 |
5999 |
27424 |
859 |
220 |
17180 |
18898 |
| 863 |
360 |
540 |
186408 |
877 |
240 |
2631 |
70160 |
| 881 |
228 |
10572 |
16739 |
883 |
225 |
15894 |
44150 |
| 887 |
230 |
8870 |
20401 |
907 |
20 |
4535 |
43536 |
| 911 |
238 |
6377 |
30974 |
919 |
231 |
60654 |
141526 |
| 929 |
240 |
13935 |
14864 |
937 |
240 |
14992 |
28110 |
| 941 |
240 |
15056 |
56460 |
947 |
240 |
28410 |
45456 |
| 953 |
248 |
7624 |
29543 |
967 |
484 |
484 |
234014 |
| 971 |
252 |
8739 |
27188 |
977 |
252 |
8793 |
82068 |
| 983 |
252 |
13762 |
35388 |
991 |
252 |
17838 |
83244 |
| 997 |
252 |
35892 |
62811 |
|
|
|
|
平成17年11月19日12時11分現在、らすかるさんは、 最終的なプログラムで、今1億
までを確認しているそうである。今のペースで行けば、3時間後ぐらいには1億までの確認
が終わるとのことで、らすかるさんからの新しい知らせが今から楽しみである。
(実際には、5時間半かかったそうです!らすかるさん、お疲れ様でした!!)
らすかるさんが作られたプログラムでは、10億とかでも一瞬で解が出るそうである。
例えば、こんな感じになるらしい。
4/1000000007=1/250000002+1/250000003750000015
+1/62500001875000021312500108750000210
4/1000000009=1/250000003+1/83333335083333346
+1/1893939473484849812500010340909122
4/1000000021=1/250000006+1/83333337083333376
+1/10416667604166698343750476250002688
4/1000000033=1/250000010+1/35714288321428620
+1/892857273214292865178746107144460
4/1000000087=1/250000022+1/250000043750001915
+1/62500021875002871312667518753665310
4/1000000093=1/250000024+1/83333349083334078
+1/10416670604167224843785169750831048
4/1000000097=1/250000025+1/83333349750000810
+1/4166668308333575954182607250392850
ところで、らすかるさんは、いろいろ試行錯誤している間に、次のような面白い事実に気
付かれたとのことである。
まず、Nが合成数については、素因数の場合の分母を定数倍すれば良い。
たとえば、 4/3=1/2+1/2+1/3 より、 4/15=1/10+1/10+1/15
一般には、素数 p に対して、 4/p=1/x+1/y+1/z のとき
4/N=4/np=1/nx+1/ny+1/nz
となるので、素数の場合のみを調べればよいが、4n+3型の素数については、実は次の
ような恒等式が成り立ち、等式を満たす自然数 X、Y、Z は必ず存在する。
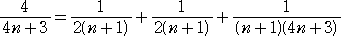
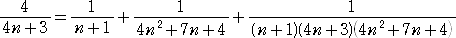
また、同様に、4n+1型の素数のうち、8m+5型の素数については
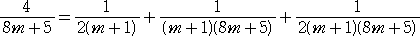
8m+1型の素数のうち、24k+17型の素数については
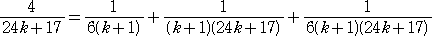
が成り立つので、等式を満たす自然数 X、Y、Z は必ず存在する。
結局は、24k+1型の素数のみを調べれば十分ということになる。
(因みに、100未満の24k+1型の素数は、実は、73と97のみであり、この2つについて
のみ調べて、後の数は上記の恒等式を用いればよかったということになる。)
ところで、この問題は、Mathworld の Unsolved Problems の中で詳しく述べられて
いるそうである。1億どころか、1014=100兆まで予想の成り立つことが既に確かめられて
いるとか...。
エルデスとシュトラウスの予想が1014=100兆まで成り立つことは、Swett(1999)に
よる。
参考文献が20年前のもので、らすかるさんにはご迷惑をおかけしました!
Swett の「The Erdos-Strauss Conjecture」の冒頭にある恒等式
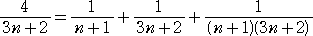
もスゴイですね!どうしたらこんな恒等式が見つけられるのでしょうか?
こんな風に、24k+1型の素数についても恒等式が見つかるといいですネ。
(参考文献: 吉永良正 著 数学のセンス (ダイヤモンド社))
(追記) 平成24年12月23日付け
任意の有理数 a/b (a、bはa<bなる自然数)は、異なる単位分数の和として
a/b=1/k1+1/k2+1/k3+・・・+1/kn
(k1、k2、k3、・・・、kn は、k1<k2<k3<・・・<kn を満たす自然数)
と表すことができる。与えられた有理数を超えない最大の単位分数を引くという操作を繰り
返せばよい。
このような入試問題が、愛知教育大学(2003)で出題された。
例 3/7、12/13をそれぞれ異なる単位分数の和として表せ。
1/3=3/9<3/7<1/2 より、 3/7−1/3=2/21
1/11=2/22<2/21<1/10 より、 2/21−1/11=1/231
よって、 3/7−1/3−1/11=1/231 より、 3/7=1/3+1/11+1/231
同様にして、 1/2=12/24<12/13<1 より、 12/13−1/2=11/26
1/3=11/33<11/26<1/2 より、 11/26−1/3=7/78
1/12=7/84<7/78<1/11 より、 7/78−1/12=6/936=1/156
よって、 12/13−1/2−1/3−1/12=1/156 より、
12/13=1/2+1/3+1/12+1/156
このような考え方を用いて、
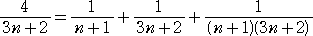
と書けることを示そうとして、いろいろ計算を行ったが、結局、文字が入っているので、
4/(3n+2)を超えない最大の単位分数は何かがわからず...挫折!
でも、そんなことにお構いなしに、
4/(3n+2)−1/(n+1)=(n+2)/{(3n+2)(n+1)}
(n+2)/{(3n+2)(n+1)}=1/(3n+2)+1/{(3n+2)(n+1)}
と分解されるので、
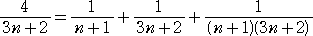
は成り立つ!結局、この等式の出自は謎のままだ。
ところで、任意の有理数 a/b (a、bはa<bなる自然数)は、異なる単位分数の和として
a/b=1/k1+1/k2+1/k3+・・・+1/kn
(k1、k2、k3、・・・、kn は、k1<k2<k3<・・・<kn を満たす自然数)
と表すことができることの証明を考えてみよう。証明してみて、上記のスッキリしない原因が
どこにあるのか分かるかもしれないので...。
(証明) まず、単位分数でない有理数 a/b (a、bはa<bなる自然数)に対して、
ある自然数 k1 (k1>1)が存在して、 1/k1<a/b<1/(k1−1)
ここで、 a/b−1/k1=a1/b1 とおくと、 a1=ak1−b 、b1=bk1
a/b<1/(k1−1) より、 a(k1−1)<b すなわち ak1−b<a なので、 a1<a
a1=1 ならば、 a/b=1/k1+1/b1
a1>1 ならば、ある自然数 k2 (k2>1)が存在して、 1/k2<a1/b1<1/(k2−1)
ここで、 a1/b1−1/k2=a2/b2 とおくと、 a2<a1
この操作を続けていくと、何れは 1=an<an-1<・・・<a2<a1 となり成り立つ。 (証終)
(コメント) 理論的には納得できるのだが、具体的にと問われると途方に暮れてしまいます
ね!
(追記) 平成25年7月29日付け
数年前からエルデスーシュトラウスの予想の完全解決に心血を注いでいられるという大学
生の方からメールを頂いた。
行き詰った頃に、このページを見つけました。その中にあったらすかるさんの作ったプログ
ラムに興味を引かれました。このプログラムで行き詰まりが解消できるかもしれないと思った
からです。らすかるさんの作られたプログラムのソースをお教えいただけないでしょうか。
(追記) 平成26年9月7日付け
真分数を2個の単位分数の和で表すことについて、都立三田高校の佐々木正敏先生が取
り組まれている。(数研通信 No.80 (数研出版))
真分数とは、値が1より小さい分数のことである。すなわち、
m/n ( m、n は互いに素な自然数で、m<n)
このとき、 m/n=1/x+1/y (x≦y) となる自然数 x、y を求めたい。
ここで、m/n を、2個の単位分数を用いて表す場合の数を、φ(m/n )と表すことにする。
例 φ(5/6)=1
例 5/66=1/14+1/231=1/15+1/990=1/22+1/33 なので、φ(5/66)=3
まず、m=1 のとき、 1/n=1/x+1/y は、(x−n)(y−n)=n2 と式変形され、その
構造は単純である。
n=pαqβ・・・rγ と素因数分解して、n2=p2αq2β・・・r2γ より、
x−n=pα1qβ1・・・rγ1 、y−n=pα2qβ2・・・rγ2 と書ける。
0≦αk≦2α、0≦βk≦2β、・・・、0≦γk≦2γ なので、x≦y を満たす自然数解の
組の個数は、
{(2α+1)(2β+1)・・・(2γ+1)−1}/2+1={(2α+1)(2β+1)・・・(2γ+1)+1}/2
したがって、 φ(1/n)=(n2の約数の個数+1)/2 であることが分かる。
例 n=4のとき、 n2=24の約数の個数は、5個なので、φ(1/4)=(5+1)/2=3
実際に、1/4=1/x+1/y において、(x−4)(y−4)=16 (x≦y) を満たす自然数解は、
(x−4,y−4)=(1,16)、(2,8)、(4,4) 即ち、 (x,y)=(5,20)、(6,12)、(8,8)
の3個あり、 1/4=1/5+1/20=1/6+1/12=1/8+1/8 と分解される
例 nが素数のとき、n2の約数の個数は、3個なので、φ(1/n)=2 となる。
次に、m=2 のとき、必然的に、nは奇数となる。このとき、
2/n=1/x+1/y は、(2x−n)(2y−n)=n2 と式変形され、その構造は、m=1の場合
と同様である。すなわち、
φ(2/n)=φ(1/n)
が成り立つ。
例 1/4=1/5+1/20=1/6+1/12=1/8+1/8 において、両辺を2倍すれば、
1/2=2/5+1/10=1/3+1/6=1/4+1/4
ここで、2/5は単位分数ではないので不適となり、 1/2=1/3+1/6=1/4+1/4
即ち、確かに、φ(1/2)=2 となっている。
一般のmについても同様の議論が可能である。
m/n=1/x+1/y は、(mx−n)(my−n)=n2 と式変形され、x≦y を満たす自然数解
を求めればよい。
特に、nが素数のとき、 (mx−n,my−n)=(1,n2)、(n,n) 即ち、
(x,y)=((n+1)/m,(n+n2)/m)、(2n/m,2n/m)
例 m=3、n=5 のとき、 (x,y)=(2,10) で、 3/5=1/2+1/10 と分解される。
すなわち、 φ(3/5)=1
例 m=5、n=6 のとき、 (5x−6)(5y−6)=36 の自然数解は、
(5x−6,5y−6)=(1,36)、(2,18)、(3,12)、(4,9)、(6,6) を解いて、
(x,y)=(2,3) のみ。
したがって、 5/6=1/2+1/3 と一意に分解される。
単位分数として、「1/2」、「1/3」は最大の2つであるので、上記から、2つの単位分数の
和で表される真分数の最大のものが、「5/6」であることが分かる。
(追記) 令和元年9月24日付け
「単位分数の和」の問題は、次の問題として考えれば馴染みやすい。
2個のケーキを5人に分ける。どのように分ければよいか。
一人分の取り分は、「2/5」で、これを単位分数の和で表すと、2/5=1/3+1/15
この式は、次のように解釈できる。
2個それぞれを3等分すると、6個の小片が出来るので、そのうちの5個をそれぞれ5人に
分ける。(→ 一人分は、1/3)
余った1個の小片を5等分して、それぞれ5人に分ける。(→ 一人分は、1/15)
すなわち、 2/5=1/3+1/15 である。
同様にして、 3/5=1/2+1/10 、4/5=1/2+1/4+1/20 などもケーキの分割を
考えれば分かりやすいかな?
(追記) 令和2年1月20日付け
単位分数の作り方を復習してみた。
4/5−1/2=8/10−5/10=3/10
3/10−1/3=9/30−10/30=−1/30<0 なので、パス
3/10−1/4=6/20−5/20=1/20
よって、 4/5=1/2+1/4+1/20
(コメント) 最大の単位分数をどんどん引いていけばいいのですね!
また、次のような方法も捨てがたい。
例 2/35を単位分数に分解せよ。
(解) 2=12/6=7/6+5/6 より、 2/35=1/30+1/42 (終)
(別解) 単位分数の和に分解するプログラムによれば、
2/35=0.057・・・ なので、0.05=1/20 より、
2/35−1/20=8/140−7/140=1/140
よって、 2/35=1/20+1/140 (終)
(追記) 令和3年6月30日付け
分数を単位分数の和に表すことを単位分数分解という。リンドパピルス(エジプト)によれ
ば、分数は単位分数のみであったという。
単位分数分解においては、
・分母はできるだけ小さい数で互いに異なる
・少ない項数に分解することが好まれ、特に、分母は偶数が望ましい
とされた。
例 5/7の単位分数分解を求めよ。
5=(1/2)×10 → 1/2を7個、3個に分ける
1/2=1/6×3 より、1/2×3=1/6×9 → 1/6を7個、2個に分ける
1/6×2=1/3=1/21×7 → 1/21を7個に分ける
以上から、5/7=1/2+1/6+1/21
読者のために、練習問題を残しておこう。
練習問題 次の分数を単位分数分解せよ。
7/8 8/9 9/10
(解) 7/8=1/2+1/4+1/8 、8/9=1/2+1/3+1/18 、
9/10=1/2+1/3+1/15 (終)
最も大切な単位分数分解は、1/3+1/6=1/2 ・・・ (*) より、1/2+1/3+1/6=1
1/3+1/6+1/6=1/2+1/6 より、 1/2+1/6=2/3
これは、2=1/2+3/2 より、 2/3=1/6+1/2 からも導かれる。
(*)×1/3 より、 1/9+1/18=1/6
(*)×1/4 より、 1/12+1/24=1/8
(*)×1/5 より、 1/15+1/30=1/10
(*)×1/6 より、 1/18+1/36=1/12
(追記) 令和3年9月30日付け
上記の 7/8=1/2+1/4+1/8 という計算は無味乾燥であるが、次のように解釈する
と、親近感が湧いてくる。
大きさの同じりんご7個を8人の子供に平等に分けなければならない。切る回数を
できるだけ少なくするにはどうすればよいか?
上記の方法と同様にして、
一人分の取り分は、「7/8」で、これを単位分数の和で表すと、7/8=1/2+1/4+1/8
この式は、次のように解釈できる。
7個それぞれを2等分すると、14個の小片が出来るので、そのうちの8個をそれぞれ8人
に分ける。(→ 一人分は、1/2)
余った6個の小片を2等分すると、12個の小片が出来るので、そのうちの8個をそれぞれ
8人に分ける。(→ 一人分は、1/4)
余った4個の小片を2等分して、それぞれ8人に分ける。(→ 一人分は、1/8)
すなわち、 7/8=1/2+1/4+1/8 である。
(追記) 「無理数での単位分数和」と題して、当HPがいつもお世話になっているHN「GAI」さ
んからご投稿いただきました。(令和3年6月30日付け)
有理数を単位分数(エジプト分数)で表す話題が上記のように出ていたので、無理数ならど
うなるか考えてみる。
ネイピアの定数eは、
e=1+1/1!+1/2!+1/3!+1/4!+1/5!+・・・=1/1+1/1+1/2+1/6+1/24+1/120+・・・
で表される。そこで、次は、円周率πは果たして小数点以下20位まで一致させるためには、
どんな単位分数の和となるか?
また、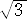 を小数点以下10位まで一致させるには?
を小数点以下10位まで一致させるには?
(コメント) 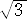 =1.73205080756888・・・ に対して、
=1.73205080756888・・・ に対して、
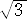 −1−1/2−1/5−1/32−1/1249−1/5989280=0.0000000000914・・・
−1−1/2−1/5−1/32−1/1249−1/5989280=0.0000000000914・・・
なので、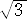 を小数点以下10位まで一致させる分数として、
を小数点以下10位まで一致させる分数として、
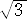 =1+1/2+1/5+1/32+1/1249+1/5989280
=1+1/2+1/5+1/32+1/1249+1/5989280
が見つかりました。
Dengan kesaktian Indukmuさんからのコメントです。(令和3年7月3日付け)
色々と考えられるところではありますけれども、例題として、ネイピアの数を引き合いに出さ
れている点を鑑みまして、これがヒントとなっているのかもと…… 探しました。
OEIS の 「A270520」あたりを使うのが面白いのでしょうか。収束が速い気持ちを込めて?
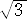 - 1 = 1/(1!*2) + 1/(2!*3) + 1/(3!*3) + 1/(4!*5) + 1/(5!*6)
- 1 = 1/(1!*2) + 1/(2!*3) + 1/(3!*3) + 1/(4!*5) + 1/(5!*6)
+ 1/(6!*14) + 1/(7!*28) + 1/(8!*352)
+・・・
左辺が、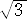 - 1 と 1 を減じている点が多少なりとも気になる向きには、OEIS の「A130738」
- 1 と 1 を減じている点が多少なりとも気になる向きには、OEIS の「A130738」
で補正をかけられます。1 を エジプト分数で(以下略)。
「A270520」では 単位分数の分母は偶数で、「A130738」では奇数になっております。
(he found them by applying EgyptOddGreedy[2/3,5] としています)
ですので、分母がぶつかることはないものと思われます。
GAI さんからのコメントです。(令和3年7月5日付け)
「1」を単位分数の和で構成することを考えると、
1=1/a1+1/a2+・・・+1/ak
但し、1<a1<a2<・・・<ak を満たす自然数[a1,a2,・・・,ak]であるものとする。
k=3 => 1=1/2+1/3+1/6 即ち [2,3,6]
k=4 => 1=1/2+1/3+1/10+1/15=1/2+1/4+1/5+1/20=1/2+1/4+1/6+1/12=etc
などいろいろ構成できるが、a1+a2+・・・+ak の数値を最も小さくするのは、これらの中で、
1/2+1/4+1/6+1/12 [2,4,6,12] での和24である。
同じく、その和を最小にするものに着目していくと、
k=5 => 1=1/3+1/4+1/5+1/6+1/20 で、[3,4,5,6,20]の38
k=6 => 1=1/3+1/4+1/6+1/10+1/12+1/15 で、[3,4,6,10,12,15]の50
そこで、k=7、8、9、10 での自然数[a1,a2,・・・,ak]をそれぞれ探してほしい。また、これは、任
意のkですぐに構成可能になるのか?
Dengan kesaktian Indukmu さんからのコメントです。(令和3年7月5日付け)
以下を見まして、見通しの良い構成方法を見つけることは難しいのではないかと感じました。
k=11 => [6,7,8,9,10,12,14,15,18,24,28]
k=12 => [6,7,9,10,11,12,14,15,18,22,28,33]
k=13 => [7,8,9,10,11,12,14,15,18,22,24,28,33]
GAI さんからのコメントです。(令和3年7月6日付け)
私も、
k=14 => [7,8,9,10,11,14,15,18,20,22,24,28,30,33]
k=15 => [7,8,10,11,12,14,15,18,20,22,24,28,30,33,36]
までは出してみましたが、これから次を求める規則性を見つけられない様に思える。
なお、この和を最小にするパターンでの和の数列が「A213062」に載せられているようだ。
(ここに載せられている数列を求めるプログラムが半端ではない。)
Dengan kesaktian Indukmu さんからのコメントです。(令和3年7月7日付け)
「A213062」の各項(分母の和)に対応する 各分母が、
「A216975」の中段に記載の「LINKS」のうちの Robert Price, Rows n = 1..24, flattened
に載っているのを見つけました。k=24 まで… どれだけ計算機を回したのでしょうか。
