
未曾有の世界恐慌に陥った2008年も何とか終わり、2009年という新しい1年が始まっ
た。これからどんなことが起こるのか時の過ぎゆくままに時代を眺めていきたい。
さて、読者の方から、「2009」にまつわる種々の話題が提供されたので、整理しておこう
と思う。
当HPにはパズルコーナーがあるが、最近新規のものをあまり更新していなかった。その
反省で、パズルを作ろうと、「2009」をいじっていたら、
2009=7×7×7×7−7×7×7−7×7
ということに気がついた。GAI さんからは、「うわー、やられた!」と言われてしまったが、
GAIさん自身も「2009」にまつわる素晴らしい関係を見いだされた。(1月4日付け)
777777≡7777777≡77777777≡777777777
≡7777777777 ・・・・・・・・・・
≡7777777777・・・
≡0 (mod 2009)
このことを証明してみよう。
77777=7×11111 において、 11111=41×271 と素因数分解される。
(→ 参考 : 「連綿と続く 1」)
さらに、 2009=72×41 であるので、
777772=72×41×41×2712=2009×41×2712
より、 777772 ≡ 0 (mod 2009) であることが分かる。
このことから、上式の全てが成り立つことは明らかだろう。
ところで、こんなにたくさん「7」が登場するのは、平成20年12月31日付けのzk43さん
の次の計算があるからだろう。
十進法で表わされる自然数は、各桁の順番を逆にして、元の数と差をとると、9で割り切
れるという性質がある。これを、2009 について考えると、
9002−2009=6993 で、9 で割ると、 6993÷9=777 (スリーセブン!)
これは、2000年代では110年に1回起こることなのだそうだ!
さらに、zk43さんは、2009 をフィボナッチ数列とも関連づけてくれた。
(平成21年1月5日付け)
数列 F(n) : 1,1,2,3,5,8,13,21,34,55,89,144,233,377,・・・
において、 F(0)=0 と考えて、フィボナッチ数列の母関数 G(x) :
を考える。このとき、 F(n+2)=F(n)+F(n+1) であるので、
x2G(x)+xG(x)+x=G(x)
すなわち、
上式に、x=1/7 を代入して、
すなわち、
となる。
(コメント) zk43さんは、7の巾 「n+3」 が美しくないと仰っていますが、
(西暦)2009(年)=(平成)21(年)=(平成)7×3(年)
と考えれば十分美しいですね!
よおすけさんは、777が3の倍数ということを示唆されたが、GAI さんは、さらに詳しく、
(西暦)2009(年)=(平成)21(年)=(平成)3×7(年)
と考えて、
3×7×37=777(ラッキーセブン!!!大当たり)
ということを見いだされた。
「7」という数字は、西洋では幸運の数とされるが、S(H)さんは、その逆数「1/7」に数学
の真理を見いだされた。(1月4日付け)
循環小数 1/7=0.1428571428571・・・・・・・ において、
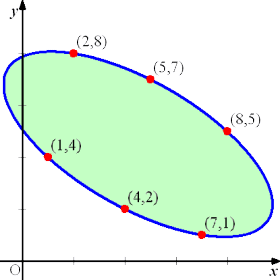
座標平面上の6個の点 (1,4)、(4,2)、(2,8)、(8,5)、(5,7)、(7,1) を考える。
このとき、この6点を通る楕円がただ1つ存在するという。
実際に、その楕円の方程式を求めると、
19x2+36xy+41y2−333x−531y+1638=0
である。
これを計算するのに、
(1,4) と (8,5) 、(4,2) と (5,7) 、(2,8) と (7,1)
の2点を結ぶ線分の中点が何れも (9/2,9/2) であることから、求める楕円の中心が、
(9/2,9/2) であることに気がつくことが肝要だろう。後は簡単な3元連立方程式を解け
ばよい。
(コメント) 1/7 から得られる6個の点が綺麗に一つの曲線上に並ぶことに数学の美し
さを感じますね!S(H)さんに感謝いたします。
ところで、循環小数 1/7 について、
1/7=0.1428571428571・・・・・・・
2/7=0.2857142857142・・・・・・・
3/7=0.4285714285714・・・・・・・
4/7=0.5714285714285・・・・・・・
5/7=0.7142857142857・・・・・・・
6/7=0.8571428571428・・・・・・・
という性質(循環節がすべて、「142857」の並びを巡回させたもの!)も面白い。
この循環節には、数字の「3」、「6」、「9」が含まれていないが、「それは、どうしてか?」
ということを今考えているところである。
この問いかけに対して、「凡人」さんが解決してくれた。(平成21年1月10日付け)
商に立つ数と余りの数に注目して表にしてみた。余りは、7倍した数より大きい最小の自
然数との差として求めた。