グラフ作成ソフトをお持ちの方へ、

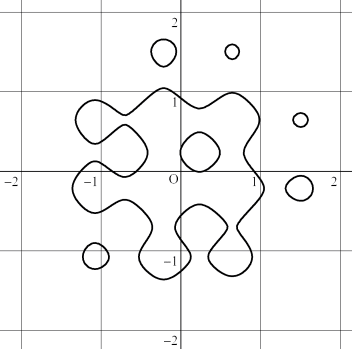
(1)　x^2+y^2+sin(7*x)+sin(7*y)-1=0

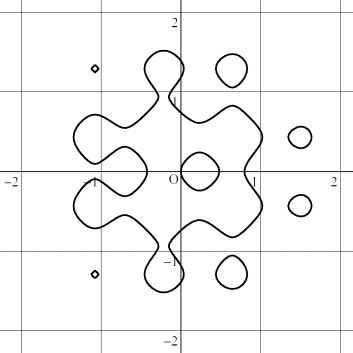
(2)　x^2+y^2+sin(7*x)+cos(7*y)-1=0

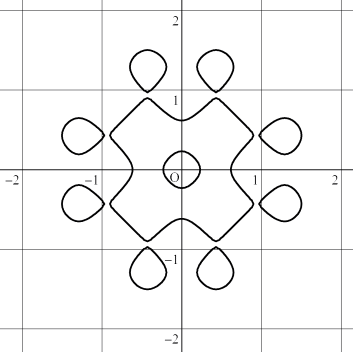
(3)　x^2+y^2+cos(7*x)+cos(7*y)-1=0

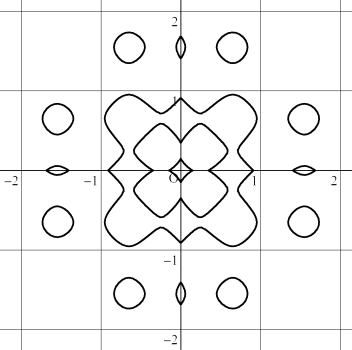
(4)　|x|+|y|+sin(|7*x|)+sin(|7*y|)-1=0

(5)　|x|+|y|+sin(|7*x|)+cos(|7*y|)-1=0

(6)　|x|*|y|+sin(|7*x|)*cos(|7*y|)-1=0

のグラフが劇的に変化する様子をお楽しみください。


（コメント）　Grapes で作画してみました。

(1)　x^2+y^2+sin(7*x)+sin(7*y)-1=0		(2)　x^2+y^2+sin(7*x)+cos(7*y)-1=0
(3)　x^2+y^2+cos(7*x)+cos(7*y)-1=0		(4)　|x|+|y|+sin(|7*x|)+sin(|7*y|)-1=0

(5)　|x|+|y|+sin(|7*x|)+cos(|7*y|)-1=0

　　

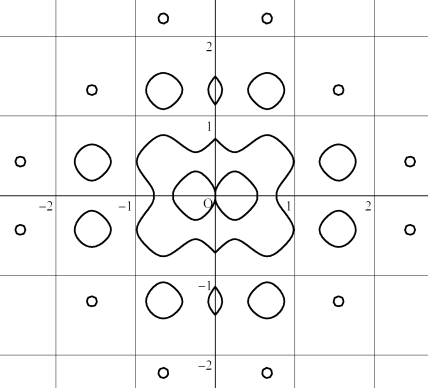
(6)　|x|*|y|+sin(|7*x|)*cos(|7*y|)-1=0

　


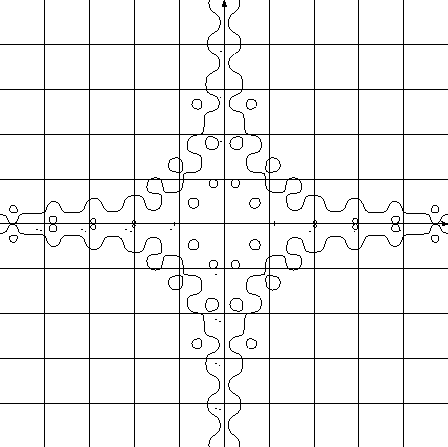
（コメント）　摩訶不思議な図形が描画できました！


　ＧＡＩ さんから新しい問題をいただきました。（令和５年９月１６日付け）

　次の９個のグラフを同時に描いてみよう。

C₁： x^2＋y^2＝9^2
C₂： (x−15)^2＋y^2＝6^2
C₃： (x−6)^2＋y^2＝15^2
C₄： (x−189/19)^2＋(y−180/19)^2＝(90/19)^2
C₅： (x−81/31)^2＋(y−360/31)^2＝(90/31)^2
C₆： (x＋33/17)^2＋(y−180/17)^2＝(30/17)^2
C₇： (x＋351/79)^2＋(y−720/79)^2＝(90/79)^2
C₈： (x＋135/23)^2＋(y−180/23)^2＝(18/23)^2
C₉： (x＋357/53)^2＋(y−360/53)^2＝(30/53)^2

　なお、これに続く３個の円の方程式は？


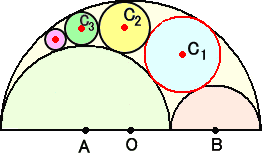
（コメント）　C₁〜C₉ について、Grapes で作画してみました。

　

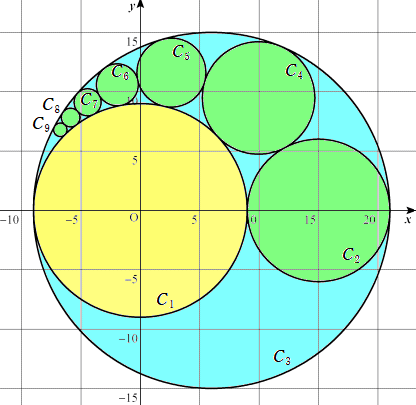
　これは、「基本の作図」の「円に接する円」の話題と同じですね！

　Ｃ₁とＣ₂からＣ₄を求めることは、既に「円に接する円」で試みられているが、ＧＡＩ さんの問
題設定で計算してみよう。求める円の半径は、解析的手法で求められる。

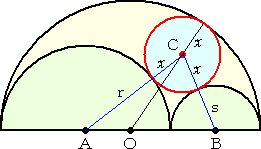△ＣＡＯと△ＣＢＯにおいて余弦定理を用いて、 　　　 　　が、求める円の半径である。

　ｒ は、円Ｃ₁の半径（＝９）で、ｓ は、円Ｃ₂の半径（＝６）なので、円Ｃ₄の半径 ｘ は、

　ｘ＝９・６・（９＋６）/（９²＋９・６＋６²）＝９０/１９

で求められる。また、円Ｃ₄の中心Ｃから直径に下ろした垂線の長さ Ｙ について

　Ｙ＝２ｘ　すなわち、垂線の長さが内接円の直径に等しい

という性質があることも興味深い。この事実は、ヘロンの公式を用いて、確かめられる。

　実際に、円Ｃ₄の中心の ｙ 座標は、「１８０/１９」で、この値は、円Ｃ₄の直径に等しい。

　１個目の円については、上記のようにヘロンの公式を用いて簡単に示すことができたが、
２個以上の場合は少し難しいように思う。（同様の手法が使えない！）

左図のように、円が順次内接するとき、その 　　内接円の半径や上記の性質を証明するには、 　　「反転」の性質を利用すると比較的平易な計算 　　で求められる。 　　　反転を用いずに、この計算を手計算で行う 　　ことは非常に辛い！！また、座標による計算 　　も膨大すぎて手に負えない．．．予感！

　上図において、円 Ｃ_ｎ の半径は、

　　　　（→　参考：「曲率の真実（反転）」）

で与えられる。

　円Ｃ₅の半径が、９０/３１であることを、上記の公式を用いて計算してみよう。

　９・６・（９＋６）/（９²＋９・６＋２²・６²）＝９０/３１　で確認できた。

　また、

　円 Ｃ_ｎ から直線ＡＢに下ろした垂線の長さは、上記の半径の ２ｎ 倍である
（→　参考：「曲率の真実（靴屋のナイフ）」）

という公式を用いると、円Ｃ₅の中心の ｙ 座標は、半径の２・２倍なので、「３６０/１９」となる

はずだが、確かに、この値は、円Ｃ₅の中心の ｙ 座標に等しい。

　以下、C₆〜C₉も同様に求めることが出来る。

　実際に、C₆の半径は、９・６・（９＋６）/（９²＋９・６＋３²・６²）＝３０/１７

　円Ｃ₆の中心の ｙ 座標は、（３０/１７）×２×３＝１８０/１７

C₇の半径は、９・６・（９＋６）/（９²＋９・６＋４²・６²）＝９０/７９

　円Ｃ₇の中心の ｙ 座標は、（９０/７９）×２×４＝７２０/７９

C₈の半径は、９・６・（９＋６）/（９²＋９・６＋５²・６²）＝１８/２３

　円Ｃ₈の中心の ｙ 座標は、（１８/２３）×２×５＝１８０/２３

C₉の半径は、９・６・（９＋６）/（９²＋９・６＋６²・６²）＝３０/５３

　円Ｃ₉の中心の ｙ 座標は、（３０/５３）×２×６＝３６０/５３


　ＧＡＩ さんの「これに続く３個の円の方程式は？」という問いかけに対しても同様の計算をす
ることによって解決することが出来る。

C₁₀の半径は、９・６・（９＋６）/（９²＋９・６＋７²・６²）＝９０/２１１

　円Ｃ₁₀の中心の ｙ 座標は、（９０/２１１）×２×７＝１２６０/２１１

C₁₁の半径は、９・６・（９＋６）/（９²＋９・６＋８²・６²）＝９０/２７１

　円Ｃ₁₁の中心の ｙ 座標は、（９０/２７１）×２×８＝１４４０/２７１

C₁₂の半径は、９・６・（９＋６）/（９²＋９・６＋９²・６²）＝３０/１１３

　円Ｃ₁₂の中心の ｙ 座標は、（３０/１１３）×２×９＝５４０/１１３


　円の半径と中心の ｙ 座標が分かれば、中心の ｘ 座標も簡単に分かる。

　例えば、C₄： (x−189/19)^2＋(y−180/19)^2＝(90/19)^2　は、次の手順で求められる。

（１）　半径の計算

　９・６・（９＋６）/（９²＋９・６＋６²）＝９０/１９

（２）　中心のｙ座標の計算

　（半径）×２×１＝１８０/１９

（３）　中心のｘ座標の計算

　三平方の定理より、　ｘ²＋（１８０/１９）²＝（９＋９０/１９）²　なので、

　ｘ²＝（２６１/１９）²−（１８０/１９）²＝８１・４４１/１９²＝（１８９/１９）²

　図より、ｘ＞０　なので、　ｘ＝１８９/１９

　他の C₅〜 についても同様である。


　らすかるさんからのコメントです。（令和５年９月１６日付け）

　ＧＡＩ さんの円C₄〜 を改めて、C’₁〜 とすると、一般式は、

　(x＋9(4n²−25)/(4n²＋15))²＋(y−180n/(4n²＋15))²＝(90/(4n²＋15))²

なので、続きは

C’₇： (x＋1539/211)^2＋(y−1260/211)^2＝(90/211)^2　（←　円C₁₀）

C’₈：(x＋2079/271)^2＋(y−1440/271)^2＝(90/271)^2　（←　円C₁₁）

C’₉：(x＋897/113)^2＋(y−540/113)^2＝(30/113)^2　（←　円C₁₂）

C’₁₀：(x＋675/83)^2＋(y−360/83)^2＝(90/415)^2

C’₁₁：(x＋4131/499)^2＋(y−1980/499)^2＝(90/499)^2

C’₁₂：(x＋1653/197)^2＋(y−720/197)^2＝(30/197)^2

C’₁₃：(x＋5859/691)^2＋(y−2340/691)^2＝(90/691)^2

C’₁₄：(x＋6831/799)^2＋(y−2520/799)^2＝(90/799)^2

C’₁₅：(x＋525/61)^2＋(y−180/61)^2＝(6/61)^2

C’₁₆：(x＋8991/1039)^2＋(y−2880/1039)^2＝(90/1039)^2

C’₁₇：(x＋10179/1171)^2＋(y−3060/1171)^2＝(90/1171)^2

C’₁₈：(x＋3813/437)^2＋(y−1080/437)^2＝(30/437)^2

　・・・・・・・・・

のようになりますね。

　一般の場合について考えてみました。

　まず、今回の設定は、最初の２円を右に９移動して、中心(15，0)、半径15の円C’₃

　((x−15)^2＋y^2＝15^2　⇔　x^2−30x＋y^2＝0)

と、中心(9，0)、半径9の円C’₁

　((x−9)^2＋y^2＝9^2　⇔　x^2−18x＋y^2＝0)

にすると、一般式は、

　((4n^2＋15)x−360)^2＋((4n^2＋15)y−180n)^2＝90^2

という綺麗な形になります。

　そして、さらに、半径も一般化すると、

　原点で接する２円：

　　中心(a，0)、半径 a の円(x^2−2ax＋y^2＝0)
　　中心(b，0)、半径 b の円(x^2−2bx＋y^2＝0)

に挟まれる円は、

((((a−b)n)^2＋ab)x−ab(a＋b))^2＋((((a−b)n)^2＋ab)y−2ab(a−b)n)^2＝(ab(a−b))^2

　n=0　が最大円、n=±1　が最大円の隣、n=±2　がその隣、・・・　のようになりました。

　a と b の大小関係はどちらでもOKですし、負でもOKです。

　a も b も負ならば、x＜0の範囲で同じことが起こり、a と b の符号が異なる場合(最初の２
円が原点で外接する場合)は、外接円で同様のことが起こります。
（つまり、n＝0 のとき、２円を包む円、n=±1 のとき、その円と元の２円に接する円、・・・）


（コメント）　らすかるさんの一般式に感謝します。

(x＋9(4n²−25)/(4n²＋15))²＋(y−180n/(4n²＋15))²＝(90/(4n²＋15))² について

（１）　半径の計算

　９・６・（９＋６）/（９²＋９・６＋ｎ²・６²）＝９０/（４ｎ²＋１５）

（２）　中心のｙ座標の計算

　（半径）×２×ｎ＝１８０ｎ/（４ｎ²＋１５）

（３）　中心のｘ座標の計算

　三平方の定理より、　ｘ²＋（１８０ｎ/（４ｎ²＋１５））²＝（９＋９０/（４ｎ²＋１５））²　なので、

　ｘ²＝（（３６ｎ²＋２２５）/（４ｎ²＋１５））²−（１８０ｎ/（４ｎ²＋１５））²

　＝（３６ｎ²＋１８０ｎ＋２２５）（３６ｎ²−１８０ｎ＋２２５）/（４ｎ²＋１５）²

　＝（６ｎ＋１５）²（６ｎ−１５）²/（４ｎ²＋１５）²

　ここで、｜６ｎ−１５｜から、ｎ≦２ において、中心は第１象限にあり、ｎ≧３ において、中心
は第２象限にあることが分かる。

　（６ｎ＋１５）（６ｎ−１５）/（４ｎ²＋１５）＝９（４ｎ²−２５）/（４ｎ²＋１５）　なので、

　何れにしても、中心の ｘ 座標は、　−９（４ｎ²−２５）/（４ｎ²＋１５）　と書ける。


　ＧＡＩ さんからのコメントです。（令和５年９月１７日付け）

　一般化された式で早速実験してみました。

　a＝-9、b＝6 で、２円を描き、n＝0 で大円が、n＝1 で３つの円に接する円が作れてくるの
ですが、n＝2、3、4、･･･ では、下方に向かって円が連なっていくのですが、これを a＝-9 の
円と大円に接する様に左に進行するようなもの（絵柄的にこちらがかっこいいので･･･)にす
るのはどうしたらいいのでしょうか？


　らすかるさんからのコメントです。（令和５年９月１７日付け）

　a＝15、b＝9 としたときの図を、左に 18 移動したものですから、

((((a−b)n)^2＋ab)x−ab(a＋b))^2＋((((a−b)n)^2＋ab)y−2ab(a−b)n)^2＝(ab(a−b))^2

の x を (x+18) にして、a＝15、b＝9 とすればいいですね。

　また、x を (x−12) にして、a＝-15、b＝-6 にすれば、反対側の円も描けます。

　一般形の式があると、こんな図も簡単に描けますが、なかったら大変ですね。

　　


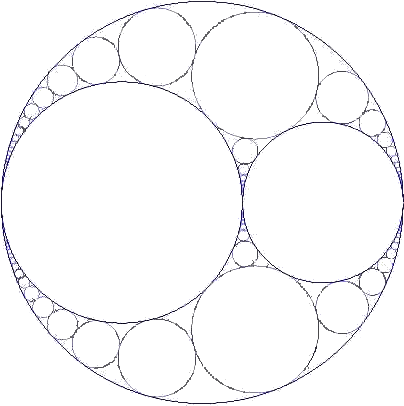
（コメント）　泡ぶくのようで、美しいです！汚れが落ちるのは、ギュウギュウ詰めの泡ぶくが
　　　　　　解放されようとするかららしいです。


　ＧＡＩ さんからのコメントです。（令和５年９月１８日付け）

　また、x を (x−12) にして、a＝-15、b＝-6 にすれば、反対側の円も描けます。

　うわー！このアイデアは思ってもいませんでした。一般化することで、応用の道が広がりま
すね〜。



　　以下、工事中！