
大学入試センター試験で、よく次のような場面設定を見かける。
垂直に関する定理 
大学入試センター試験で、よく次のような場面設定を見かける。
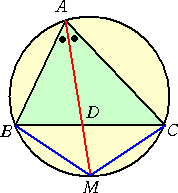 |
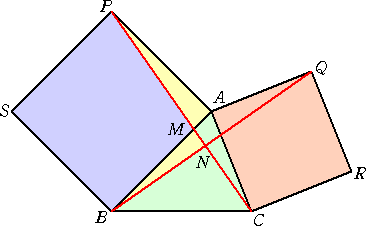
△ABCの外接円と∠Aの2等分線の交点をMとし、 AMと辺BCの交点をDとする。 この場面設定だと、角の2等分の性質を利用させる問題や 円周角の性質を用いて正弦や余弦、はたまた面積などを求 めさせたり、いろいろな問題が湧出してくる。 多分、センター試験出題者にとってはまさにドル箱の図形と 言っても言い過ぎではないだろう。 |
この有名すぎる場面設定で、次のような公式が成り立つことを最近知ることが出来た。
AM2=AB・AC+BM2
この公式は、さらに豊かな応用を秘めており、私の備忘録に記録することにした。
こういう性質は受験場ではなかなか思いつかないもの。知っていれば、大学入試センター
試験で有利になる可能性は十分あるだろうし、また、美しい性質ゆえ図形に対する愛着も
湧いてくることだろう。
(証明) △ABM∽△BDM より、AM : BM = BM : DM なので、BM2 = AM・DM
また、△ABD∽△AMC より、 AB : AD = AM : AC なので、AB・AC = AD・AM
よって、 AB・AC+BM2 = AD・AM+AM・DM = AM・(AD+DM) = AM2 (証終)
さらに、次の性質も面白い。
AD2=AB・AC−BD・DC
(証明) △ABD∽△AMC より、 AB : AM = AD : AC なので、
AB・AC = AD・AM = AD・(AD+DM) = AD2+AD・DM
方べきの定理より、 AD・DM = BD・DC なので、AB・AC = AD2+BD・DC
すなわち、 AD2 = AB・AC−BD・DC が成り立つ。 (証終)
特に、△ABC が、 AB=AC の2等辺三角形のとき、
AB2=AD・AM
なお、この性質は、AM が∠Aの2等分線でない場合も成立する。
(証明)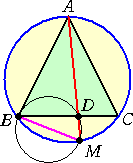 |
左図において、 ∠ABD=∠ACD=∠BMD なので、 接弦定理より、ABは、3点 B、M、D を通る円の接線である。 よって、方べきの定理より、 AB2=AD・AM が成り立つ。 (証終) |
今、平面上に相異なる4点 A 、B 、C 、D があり、 AB⊥CD とする。
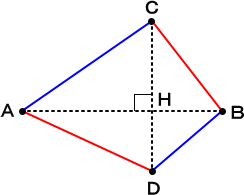
このとき、 AC2+BD2=AD2+BC2 が成り立つ。
(証明) 三平方の定理より、
AC2+BD2=AH2+HC2+BH2+HD2
AD2+BC2=AH2+HD2+BH2+HC2
なので、 AC2+BD2=AD2+BC2 が成り立つ。 (証終)
ここで興味深いことは、この逆が成り立つことである。
すなわち、
平面上の相異なる4点 A 、B 、C 、D に対して、 AC2+BD2=AD2+BC2 が
成り立つとき、 AB⊥CD が成り立つ。
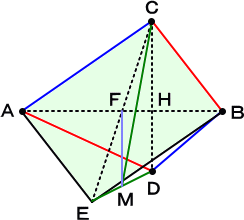
(証明) 上図のように、平行四辺形 AEBC を作り、対角線の交点を F とする。
また、線分 DE の中点を M とおく。このとき、中線定理と、AC2+BD2=AD2+BC2 より、
2(AM2+MD2)=AD2+AE2=AD2+BC2=AC2+BD2=BE2+BD2
=2(BM2+MD2)
よって、 AM=BM が成り立ち、 △AMF≡△BMF となる。
このとき、 AB⊥FM である。
ところで、 中点連結の定理より、 FM‖CD なので、 AB⊥CD となる。 (証終)
以上の準備の下に、いくつかの問題を考える。
△ABC の辺 AB の中点を D とし、3点 A、B、D および A、C、D を通る円を描く。
下図のように、弧AB、弧AC の中点をそれぞれ M、N とおく。
このとき、 MN⊥AD となることを証明せよ。
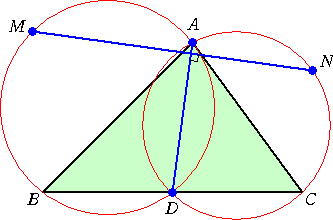
意外なところに「垂直」が現れて、その美しさに感動を覚える!
(証明) 題意より、 DM2=DA・DB+AM2 、DN2=DA・DC+AN2
DB=DC なので、 DM2−AM2=DN2−AN2
すなわち、 DM2+AN2=DN2+AM2 が成り立つ。
よって、 MN⊥AD である。 (証終)
ABを直径とする円周上に、AP=AQ となるように2点 P、Q をとり、線分 PQ 上
の任意の点を C とする。点 C より、 AQ 、AP に平行に直線を引き、AP 、AQ と
の交点をそれぞれ M 、N とおく。このとき、 MN⊥BC となることを証明せよ。
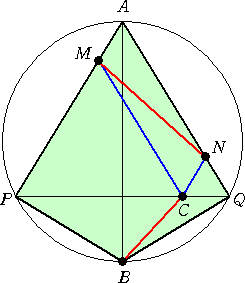
この「垂直」にも意外性が感じられますね!
(証明) 題意より、 BP=BQ 、MP=MC 、NC=NQ が成り立つ。
また、 BM2=BP2+MP2=BQ2+MC2
BN2=BQ2+NQ2=BQ2+NC2
よって、 BM2−BN2=MC2−NC2 より、 BM2+NC2=BN2+MC2 なので、
MN⊥BC である。 (証終)
(コメント) 4点 B、C、M、N がどんな位置にあっても、BM2+NC2=BN2+MC2 が
成り立っていれば、純粋に、MN⊥BC なんですね!
円に内接する四角形 ABCD において、対角線 AC と BD の交点を M とする。
また、△ABM の外接円の中心を N とおく。このとき、 MN⊥CD となることを証
明せよ。
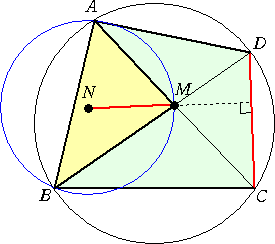
これは、ちょっと気がつきにくい「垂直」ですね!
(証明) 点 C より、円 N に引いた接線の接点を T とすると、方べきの定理より、
CT2=CM・CA なので、 CN2−NT2=CM・CA
すなわち、 CN2−NM2=CM・CA=CM・(CM+MA)=CM2+CM・MA
同様にして、 DN2−NM2=DM・DB=DM・(DM+MB)=DM2+DM・MB
また、方べきの定理より、 CM・MA=DM・MB なので、
CN2−DN2=CM2−DM2 すなわち、 CM2+DN2=CN2+DM2
となり、よって、MN⊥CD である。 (証終)
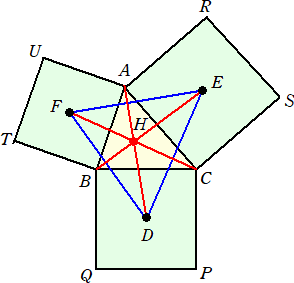
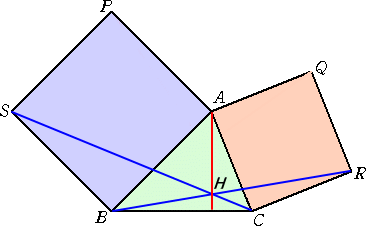
△ABC の各辺を斜辺とする直角2等辺三角形を △ABC の外部に作る。
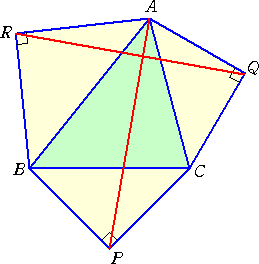
このとき、 AP⊥QR となることを証明せよ。
この場合も、「垂直っぽいけど、ホントに垂直...?」という感じである。
(証明) 余弦定理より、
PQ2=PC2+CQ2−2PC・CQ・cos∠PCQ
=PC2+CQ2−2PC・CQ・cos(90°+∠ACB)
=PC2+CQ2+2PC・CQ・sin∠ACB
=PC2+CQ2+(![]() PC)・(
PC)・(![]() CQ)・sin∠ACB
CQ)・sin∠ACB
=PC2+CQ2+CB・CA・sin∠ACB
=PC2+CQ2+2△ABC
同様にして、 PR2=PB2+BR2+2△ABC
よって、 PQ2−PR2=PC2+CQ2−PB2−BR2=CQ2−BR2=AQ2−AR2
このとき、 AR2+PQ2=AQ2+PR2 となり、 AP⊥QR である。 (証終)
| ブラマグプタの定理 円に内接する四角形 ABCD の対角線 AC、BD が直交している。 このとき、 その交点 P を通って辺 CD に垂直な直線 は辺 AB の中点を通る。 |
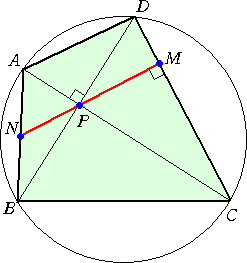 |
(証明) ∠NAP=∠PDM=∠CPM=∠NPA より、
△NPAは2等辺三角形で、 NA=NP
同様にして、 ∠NBP=∠PCM=∠DPM=∠NPB より、
△NBPは2等辺三角形で、 NB=NP
よって、 NA=NB となり、 N は辺 AB の中点となる。 (証終)
(コメント) ブラマグプタというと、面積の公式が有名(→参考:「ブラマグプタの公式」)です
が、こういう定理もあったんですね!
このブラマグプタの定理は次のような形に 一般化される。 円に内接する四角形 ABCD の対角 線の交点 P を通り、辺 CD に垂直な直 線は △PAB の外心を通る。 |
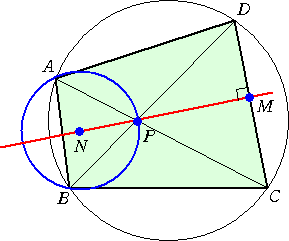 |
(証明)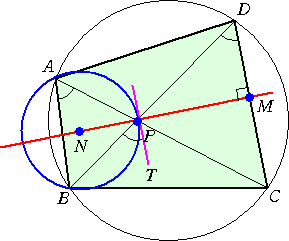 |
左図において、PTを接線とすると、 接弦定理より、 ∠BPT=∠BAP また、円周角の定理より、 ∠BAP=∠BDC よって、 ∠BPT=∠BDC となり、 PT‖DC である。 PM⊥PT なので、 直線PMは△PABの外心を通る。 (証終) |
次の「垂直」も面白い。
△ABC の頂点 A を通る任意の直線に、頂点 B、C から垂線を下ろし、その足を
それぞれ D、E とする。点 D、E からそれぞれ辺 AC、AB に垂線を下ろし、その交
点を F とする。このとき、 AF⊥BC となることを証明せよ。
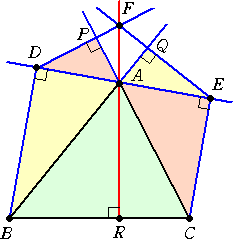
(証明) 4点 B、E、Q、D は同一円周上にある。同様に、4点 C、E、P、D
も同一円周上
にある。 よって、方べきの定理より、BA・AQ=EA・AD かつ CA・AP=EA・AD
よって、 BA・AQ=CA・AP が成り立つ。
すなわち、方べきの定理より、4点 B、C、Q、P は同一円周上にある。
よって、 ∠ABC=∠APQ が成り立つ。
ここで、4点 A、Q、F、P は同一円周上にあるので、 ∠APQ=∠AFQ
よって、 ∠ABC=∠AFQ が成り立つ。
△ABR と △AFQ において、 ∠ABR=∠AFQ かつ ∠BAR=∠FAQ なので、
△ABR ∽ △AFQ となり、よって、 ∠ARB=∠AQF=90°である。
したがって、 AF⊥BC が成り立つ。 (証終)
下図のような、AB=ACの二等辺三角形ABCにおいて、頂点Aより辺BCに垂線
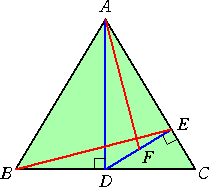 |
ADを下ろし、さらに、点Dより辺ACに垂線DEを下ろ す。線分DEの中点を F とする。このとき、 AF⊥BE となることを証明せよ。 (証明は、「適切な座標系」を参照) |
「適切な座標系」では座標系を上手く設定して解析幾何的に解いたり、あるいはベクトル
を用いて軽妙に解いた。
あまりお勧め出来ない方法であるが、
平面上の相異なる4点 A 、B 、C 、D
に対して、 AC2+BD2=AD2+BC2 が
成り立つとき、 AB⊥CD が成り立つ。
という事実を用いても当然証明されうる。
(証明) BD=DC=a 、AD=b 、∠DCE=θ とおくと、 ![]() なので、
なので、
![]()
![]()
このとき、
![]()
![]()
また、∠BDF=180°−(90°−θ)=90°+θ なので、△BDFに余弦定理を適用して、
BF2=BD2+DF2−2・BD・DF・cos(90°+θ)
より、
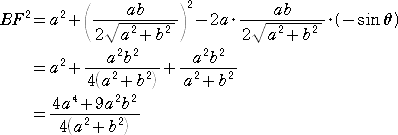
よって、
![]()
![]()
より、 AB2+EF2=AE2+BF2 が成り立つ。
したがって、 AF⊥BE が成り立つ。 (証終)
また、次の「垂直」も面白い。
△ABC において、辺AB、辺ACを1辺とする正方形ABSR、ACRQ を三角形の
外部に作る。辺BCおよび線分PQの中点をそれぞれM、Nとおくとき、
AM⊥PQ 、 PQ=2AM 、 AN⊥BC 、 BC=2AN
となることを証明せよ。
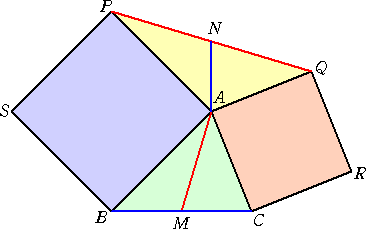
この証明を考えるとき、複素数平面を知っていると非常に楽であることに気づく。複素数
平面が新学習指導要領から消えてしまったことが残念でならない。
(証明) 複素数平面において、Aを原点とし、B( 2β )、C( 2γ )とする。
このとき、 P( −2iβ ) 、 Q( 2iγ ) (ただし、 i は虚数単位) が成り立つ。
よって、 M( β+γ ) 、 N( i(γ−β) ) である。
このとき、PQ/AM=2i(γ+β)/(β+γ)=2i より、 AM⊥PQ 、 PQ=2AM が
成り立つ。同様にして、BC/AN=2(γ−β)/{i(γ−β)}=−2i より、
AN⊥BC 、 BC=2AN が成り立つ。 (証終)
この手法を用いると、いろいろな「垂直」が楽しめそうな...予感。
△ABC において、辺AB、辺ACを1辺とする正方形ABSR、ACRQ を三角形の
外部に作る。このとき、 BQ⊥CP 、 BQ=CP となることを証明せよ。
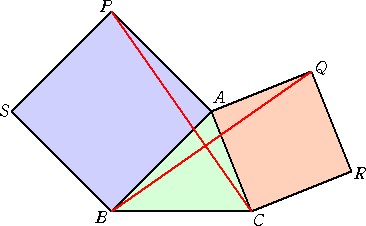
(証明) 複素数平面において、Aを原点とし、B( β )、C( γ )とする。
このとき、 P( −iβ ) 、 Q( iγ ) (ただし、 i は虚数単位) が成り立つ。
このとき、BQ/PC=(iγ−β)/(γ+iβ)= i より、
BQ⊥PC 、 BQ=PC が成り立つ。 (証終)
(コメント) 複素数を使わないとすると、 BQ=PC は、△ABQ≡△APC から明らかだ
が、BQ⊥PC を示すためには別な三角形を用いないといけない!
△APM ∽ △NBM なので、 ∠MNB=∠MAP=90° から、 BQ⊥PC
このように考えると、複素数を使う場合が、いかにエレガントかが思い知らされる。
(追記) 令和3年4月16日付け
上記の複素数平面を利用した解法の類題を考えよう。
正三角形ABCの各辺の外側に正方形BCPQ、CARS、ABUVを描き、各正方形の中心を
それぞれD、E、Fとおく。このとき、
AD⊥EF 、BE⊥FD 、CF⊥DE
が成り立つことは自明だろう。3直線AD、BE、CFは1点Hで交わり、点Hは△DEFの垂心
となる。
実は、この事実は、正三角形のみならず、一般の三角形においても成り立つ。
定理 △ABCの各辺の外側に正方形BCPQ、CARS、ABTUを描き、各正方形の
中心をそれぞれD、E、Fとおく。このとき、
AD⊥EF 、BE⊥FD 、CF⊥DE
が成り立つ。
(証明) 複素数平面において、A( 2α )、B( 2β )、C( 2γ )とする。
このとき、 P( 2γ+2i(β−γ) ) 、Q( 2β−2i(γ−β) ) (ただし、 i は虚数単位)
なので、 D(β+γ+i(β−γ)) が成り立つ。
同様にして、 E(γ+α+i(γ−α)) 、F(α+β+i(α−β)) が成り立つ。
よって、 EF=β−γ+i(2α−β−γ) 、AD=−2α+β+γ+i(β−γ) より、
i・EF=AD なので、 AD⊥EF が成り立つ。
同様にして、
i・FD=BE i・DE=CF なので、BE⊥FD 、CF⊥DE が成り立つ。 (証終)
証明の中で示されたことから、 AD=EF、BE=FD、CF=DE であることも分かる。
上記では、一般の三角形であったが、一般の四角形においても次のような性質が言える。
四角形ABCDの各辺の外側に正方形を描く。このとき、相対する正方形の中心を
結ぶ線分は、長さが等しく、かつ、垂直である。
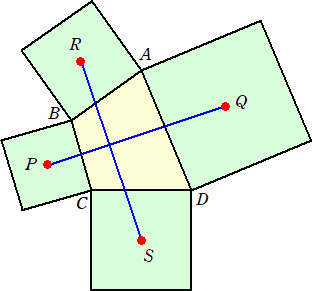
(証明) 複素数平面において、A( 2α )、B( 2β )、C( 2γ )、D(2δ)とする。
このとき、 i を虚数単位として、
P( β+γ+i(β−γ) ) 、Q(δ+α+i(δ−α) ) 、R(α+β+i(α−β))
S(γ+δ+i(γ−δ))
なので、 PQ=α−β−γ+δ+i(−α−β+γ+δ)
SR=α+β−γ−δ+i(α−β−γ+δ)
が成り立つ。よって、 i・PQ=SR なので、 PQ=SR かつ PQ⊥SR (証終)
読者の方のために、練習問題を残しておこう。
練習問題 △ABCの辺AB、ACの外側に正方形ABSP、ACRQを描き、線分BRとCS
の交点をHとする。このとき、 AH⊥BC が成り立つことを示せ。
(解) 複素数平面において、A( α )、B( β )、C( γ )、H(δ)とする。
このとき、 S( β+i(α−β) ) 、R( γ−i(α−γ) ) (ただし、 i は虚数単位)
S、H、Cが一直線上にあるので、 (β+i(α−β)−γ)/(δ−γ) は実数となる。
すなわち、 (β+i(α−β)−γ)/(δ−γ)=(β~−i(α~−β~)−γ~)/(δ~−γ~)
が成り立つ。ただし、α~は、αの共役複素数とする。
分母を払って、
δ(β~−γ~)−δ~(β−γ)−β~γ+βγ~
=i・(δ(α~−β~)−γ(α~−β~)+δ~(α−β)−γ~(α−β)) ・・・ (*)
同様に、B、H、Rが一直線上にあるので、 (γ−i(α−γ) −β)/(δ−β) は実数
なので、 (γ−i(α−γ) −β)/(δ−β)=(γ~+i(α~−γ~) −β~)/(δ~−β~)
分母を払って、
δ(γ~−β~)−δ~(γ−β)+β~γ−βγ~
=i・(−δ(α~−γ~)+β(α~−γ~)−δ~(α−γ)+β~(α−γ)) ・・・ (**)
(*)と(**)を辺々加えて、
0=i・(δ(γ~−β~)+δ~(γ−β)−α(γ~−β~)−α~(γ−β))
よって、 (δ−α)(γ~−β~)+(δ~−α~)(γ−β)=0 から、
(δ−α)/(γ−β)=−(δ~−α~)/(γ~−β~)
すなわち、 arg(δ−α)/(γ−β)=±π/2 となり、AH⊥BC が成り立つ。 (終)
(追記) 令和6年7月12日付け
数列と垂直の融合問題が、東北大学 文理共通(1967)で出題された。
第2問 楕円 x2/25+y2/9=1 上の相異なる3点A(x1,y1)、B(4,9/5)、C(x2,y2)
から焦点F(4,0)にいたる距離は、この順に等差数列をなすものとする。
(1) x1+x2=8 を示せ。
(2) また、線分ACの垂直2等分線が x 軸と交わる点をTとするとき、直線BTの傾きを求
めよ。
(解)(1) 題意より、 y12=9−(9/25)x12 、y22=9−(9/25)x22 なので、
(x1−4)2+y12=x12−8x1+16+9−(9/25)x12=(16/25)x12−8x1+25
=(16/25){(x12)−(25/2)x1+625/16}=(16/25)(x1−25/4)2
x1−25/4<0 より、 AF=√((x1−4)2+y12)=(4/5)(25/4−x1)
同様にして、 CF=√((x2−4)2+y22)=(4/5)(25/4−x2)
数列 AF、BF、CF は等差数列なので、 AF+CF=2BF=18/5
よって、 (4/5)(25/4−x1)+(4/5)(25/4−x2)=18/5
すなわち、 25/2−(x1+x2)=9/2 より、 x1+x2=8 が成り立つ。
(2) 線分ACの中点は、(4,(y1+y2)/2)なので、線分ACの垂直2等分線の方程式は、
y=−{(x1−x2)/(y1−y2)}(x−4)+(y1+y2)/2
ここで、y=0 とおいて、
x=4+(y12−y22)/(2(x1−x2))
=4−(9/25)(x12−x22)/(2(x1−x2))=4−36/25=64/25
より、 T(64/25,0) となる。
このとき、直線BTの傾きは、 (9/5)/(4−64/25)=(9/5)÷(36/25)=5/4 (終)
(コメント) よく練られた美しい結果ですね!
次の東北大学 文理共通(1967)の問題も、垂直に関する定理と言える。
第3問 直角三角形ABCの辺BCの中点をMとする。辺AB、AC上にそれぞれ点P、Qを
とり、点P、Qから辺ABに下した垂線の足をP’、Q’とする。このとき、点P’、Q’は、
P’Q’=(1/2)BC を満たしているものとする。
いま、MP=p、MQ=q、MC=c とおく。
(1) P’Q’=(1/2)BC なる関係を、内積を用いて、c、p、q で表せ。
(2) また、MPとMQはつねに直交することを示せ。
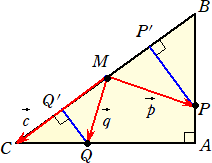
(解)(1) PQ・P’Q’=PQ・P’Q’cos(PQ、P’Q’のなす角)=P’Q’2=c・c より、
P’Q’=(1/2)BC=c より、 (q−p)・c=c・c
(2) BP⊥CQ より、 (p+c)・(q−c)=0 なので、 p・q+(q−p)・c−c・c=0
(1)より、 (q−p)・c−c・c=0 なので、 p・q=0
したがって、MPとMQはつねに直交する。 (終)
(コメント) P’Q’=(1/2)BC が成り立つとき、MP⊥MQになるんですね!美しい結果です。
以下、工事中!