廃偺挿偝堦掕側恾宍 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暯惉侾俉擭俇寧俀俈擔丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵壛弐偝傫偑栤戣傪採婲偝傟偨丅
丂妛峑婣傝偵桭恖偲榖偟偰偄偰丄師偺偙偲偑榖戣偵側偭偨偲偄偆丅
丂廃偺挿偝偑堦掕側恾宍偱嵟戝柺愊傪帩偮偺偼墌偲偄偆偺偼桳柤偱偁傞丅偠傖偁丄偦偺媡
偼丠偲偄偆偙偲偱師偺媈栤偑惗傑傟偨丅
丂丂乽摨懱愊偺棫懱偱丄嵟傕昞柺愊偑戝偒偔側傞恾宍偼壗偐丠乿
丂偦偺偲偒偼丄廮栄尒偨偄側姶偠丠偲偄偆偁偄傑偄側摎偊偱廔傢偭偰偟偭偨偑丄偙傟偱偼擺
摼偱偒側偐偭偨偺偱丄偦偺屻偠偭偔傝峫偊偰傒偨丅傗偼傝廮栄偺栄偺傛偆偵嶌偭偨僔乕僩忬
偺暔傪丄傑偨廮栄偺傛偆偵愜傝曉偟丄嵞傃僔乕僩忬偵偡傞乧傪孞傝曉偟偨恾宍偲偄偆峫偊偵
偨偳傝拝偄偨丅側傫偐僼儔僋僞儖偺傛偆偵傕姶偠傞偑丄偳偆偩傠偆偐丠
丂壛弐偝傫偑僼儔僋僞儖偺傛偆偩偲姶偠傜傟偨姶妎偼惓偟偄偲巚偆丅偨偩丄暯柺偱壓婰偺傛
偆側椺偑偁傞偺偱丄嬻娫恾宍偱嵟戝偺昞柺愊偑偁傞偲偼峫偊偵偔偄丅
椺丂暯柺偵偍偄偰丄壓恾偺傛偆側恾宍傪峫偊傞丅
丂丂 |
丂丂嵍恾偵偍偄偰丄柺愊偼侾偱堦掕偱偁傞
丂偑丄廃偺挿偝偼丄俀値亄俁偱偁傞丅
丂丂偙偺偙偲偐傜丄値傪尷傝側偔戝偒偔偡傞偲丄
丂廃偺挿偝傕尷傝側偔戝偒偔側傞丅
丂丂偟偨偑偭偰丄柺愊偑堦掕側偺偵丄偦偺
丂廃偺挿偝偵偼嵟戝抣偑懚嵼偟側偄丅
|
丂偦偆尵偊偽丄愄撉傫偩榖偺拞偵師偺傛偆側傕偺偑偁偭偨丅
丂墹條偐傜丄媿侾摍暘偺旂偱暍傢傟傞搚抧傪梌偊傛偆偲偄偆偛朖旤傪傕傜偭偨抦宐幰偑丄媿
偺旂傪嵶偔挿偔愗偭偰丄偦傟偱暍傢傟傞峀戝側搚抧傪庤偵擖傟偨偲偄偆丅墹條偺巚榝偲堘偄丄
墹條偼戝曄崲偭偨偲偺偙偲偱偁傞丅
丂暯惉侾俉擭俇寧俁侽擔晅偗偱丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞枹嵷幚偝傫偐傜傾僪僶僀僗
傪捀偄偨丅枹嵷幚偝傫偵姶幱偟傑偡丅
丂榖戣偵捈愙娭學偡傞偐偳偆偐傢偐傝傑偣傫偑丄
丂丂僈乕僪僫乕偺乽僗僼傿儞僋僗偺撲乿丂9.僇儖僇僢僞乕偺僽儔僢僋儂乕儖
偵懱愊偑桳尷偱昞柺愊傗挿偝偑柍尷偵側傞3師尦恾宍偺榖偑弌偰偄傑偡丅
乮忋婰偺彂愋偼尰嵼擖庤晄壜擻偱恾彂娰摍偱墈棗偡傞偟偐側偄傛偆偩両乯
丂壛弐偝傫偵怗敪偝傟偰丄廃偺挿偝偑堦掕側恾宍偵偮偄偰挷傋偰傒傛偆偲巚偄棫偭偨丅
丂摉俫俹偱偼丄乽儔僌儔儞僕儏偺忔悢乿偵偍偄偰丄乽廃偺挿偝偑 俇 偺嶰妏宍偱柺愊偑嵟戝偱
偁傞傕偺傪媮傔傞乿偲偄偆栤戣傪峫偊偨丅
丂俴倎倗倰倎値倗倕 偺枹掕忔悢朄乮戝妛侾擭偺旝暘愊暘妛偺儗儀儖乯傪梡偄傞偲師偺傛偆偵慛傗偐
偵夝偐傟傞丅
丂乮栤戣愝掕乯
丂俁曈偺挿偝丂倶 丆 倷 丆 倸丂偺嶰妏宍偵偍偄偰丄丂倶 亄 倷 亄 倸 亖俇丂偺偲偒丄偦偺嶰妏宍偺柺
愊偺暯曽偼丄僿儘儞偺岞幃傛傝丄丂俁(俁亅 倶 )(俁亅 倷 )(俁亅 倸 )丂偱梌偊傜傟傞丅
丂俁(俁亅 倶 )(俁亅 倷 )(俁亅 倸 )丂偑嵟戝偲側傞偺偼丄偳傫側応崌偐丠
乮夝乯丂俧乮 倶 丆 倷 丆 倸 乯亖倶 亄 倷 亄 倸 亅俇亖侽丂偺偲偒丄
丂俥乮 倶 丆 倷 丆 倸 乯亖俁(俁亅 倶 )(俁亅 倷 )(俁亅 倸 )丂偺嬌抣傪梌偊傞揰乮倎 丆 倐 丆 們 乯偼師偺幃
傪枮偨偡丅
丂倶 亄 倷 亄 倸 亅俇亖侽丂丄亅俁(俁亅 倷 )(俁亅 倸 )亄兩亖侽丂丄亅俁(俁亅倶 )(俁亅 倸 )亄兩亖侽
丂亅俁(俁亅 倶 )(俁亅 倷 )亄兩亖侽
丂倶 亗 俁丂丄倷 亗 俁丂丄倸 亗 俁丂偲偟偰傛偄偺偱丄忋幃偐傜丄丂倶亖 倷 亖 倸 亖俀丂丄兩亖俁丂偱
偁傞偙偲偑梕堈偵暘偐傞丅
丂婔壗妛揑偵峫偊偰丄倶 亖 倷 亖 倸 亖俀丂偡側傢偪丄惓嶰妏宍偺偲偒丄柺愊偼嬌戝偐偮嵟戝
偲側傞丅丂丂乮廔乯
丂偙偺偙偲傪堦斒壔偡傟偽丄
丂丂廃偺挿偝偑堦掕側嶰妏宍偱柺愊偑嵟戝側傕偺偼丄惓嶰妏宍偱偁傞
偙偲偑暘偐傞丅
忋婰偱偼丄俴倎倗倰倎値倗倕 偺枹掕忔悢朄傪梡偄偨偑丄崅峑惗儗儀儖偺徹柧傕壜擻偩丅
乮暿夝乯丂嶰妏宍偺俁曈偺挿偝傪丂倶 丆 倷 丆 倸丂偲偟丄丂倶 亄 倷 亄 倸
亖俀俴丂偲偡傞偲丄
丂偦偺嶰妏宍偺柺愊 俽 偺暯曽偼丄僿儘儞偺岞幃傛傝丄
丂丂俽2亖俴乮俴亅倶乯乮俴亅倷乯乮俴亅倸乯亖俴乮俴亅倶乯乮俴亅倷乯乮倶亄倷亅俴乯
丂丂偨偩偟丄丂侽亙倶亙俴丂丄侽亙倷亙俴丂丄倶亄倷亜俴
偱梌偊傜傟傞丅
丂偙偙偱丄暵椞堟丂侽亝倶亝俴丂丄侽亝倷亝俴丂丄倶亄倷亞俴丂偵偍偄偰丄俽2 偼丄嵟戝抣傪帩偮丅
丂憡壛暯嬒偲憡忔暯嬒偺娭學偐傜丄
丂丂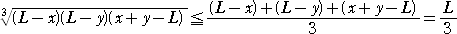
偟偨偑偭偰丄丂俴亅倶亖俴亅倷亖倶亄倷亅俴丂偡側傢偪丄丂倶 亖 倷 亖 倸 亖 俀俴/俁丂偺偲偒丄
柺愊 俽 偼嵟戝偲側傞丅丂偙偺偲偒丄嶰妏宍偼惓嶰妏宍偱偁傞丅丂丂乮廔乯
乮捛婰乯丂暯惉俀俈擭侾侽寧侾侽擔晅偗
丂忋婰偱偼丄廃偺挿偝偑堦掕側嶰妏宍偱柺愊偑嵟戝偲側傞傕偺偼惓嶰妏宍偱偁傞偙偲傪丄
俴倎倗倰倎値倗倕 偺枹掕忔悢朄傗憡壛丒憡忔偺暯嬒偺晄摍幃傪梡偄偰帵偟偨偑丄師偺傛偆偵峫
偊傟偽捈姶揑偵傕柧傜偐偩傠偆丅
丂嶰妏宍偺侾曈傪屌掕偡傟偽丄柺愊偑嵟戝偵側傞偺偼丄擇摍曈嶰妏宍偩偐傜丄偳偺曈偐傜
尒偰傕擇摍曈嶰妏宍偲側傞嶰妏宍偼丄惓嶰妏宍偵尷傞丅
丂偙偺傛偆側夝朄偼摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞 倀 偝傫偵偼晄昡偺傛偆偱丄俴倎倗倰倎値倗倕
偺枹掕忔悢朄傪梡偄傞曽偑敪憐偑帺慠偱偁傞偲弎傋傜傟偰偄傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮摉俫俹宖帵斅乽弌夛偄偺愹乿丗暯惉侾俉擭俈寧俀擔晅偗乯
丂侾俋俉係擭搙偺悢妛僆儕儞僺僢僋偱丄師偺傛偆側栤戣偑弌戣偝傟偨偦偆偩丅
丂丂倶 丆 倷 丆 倸丂偑丄 倶 亄 倷 亄 倸 亖 侾丂傪枮偨偡旕晧偺幚悢偱偁傞偲偒丄
丂丂侽亝倶倷亄倷倸亄倸倶亅俀倶倷倸亝俈/俀俈
偑惉傝棫偮偙偲傪帵偣丅
丂悢妛僆儕儞僺僢僋偼丄崅峑掱搙偺梊旛抦幆傪憐掕偟偰偄傞偺偱丄偙偺栤戣偵丄儔僌儔儞僕儏
偺忔悢傪揔梡偡傞偺偼柍棟偑偁傞偩傠偆丅
丂倀 偝傫偵偼乽偙傟偼丄偪傚偭偲僱丏丏丏丅乿偲偄偆夝朄偩偑丄巹帺恎偼師偺傛偆側夝朄偺慛傗偐偝
偵堷偐傟傞曽偩丅
* 暯惉俀俀擭俁寧係擔晅偗偺俫俶乽偒傚備偵乿偝傫偺偛巜揈傪庴偗偰丄埲壓偺徹柧傪堦晹庤捈偟偟傑偟偨丅
乮徹乯丂忦審傛傝丄丂侽亝倶亝侾丂丄侽亝倷亝侾丂丄侽亝倸亝侾丂側偺偱丄
丂亅侾亝侾亅俀倶亝侾丂丄亅侾亝侾亅俀倷亝侾丂丄亅侾亝侾亅俀倸亝侾丂傛傝丄
丂亅侾亝乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯亝侾丂偑惉傝棫偮丅
丂傑偨丄
乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯
亖侾亅俀乮倶亄倷亄倸乯亄係乮倶倷亄倷倸亄倸倶乯亅俉倶倷倸亖係乮倶倷亄倷倸亄倸倶乯亅俉倶倷倸亅侾
傛偭偰丄丂倶倷亄倷倸亄倸倶亅俀倶倷倸亖乷乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯亄侾乸/係
偟偨偑偭偰丄丂倶倷亄倷倸亄倸倶亅俀倶倷倸亞侽丂偑惉傝棫偮丅
傑偨丄丂倶倷亄倷倸亄倸倶亅俀倶倷倸丂偺嵟戝抣傪媮傔傞偨傔偵偼丄
丂倶倷亄倷倸亄倸倶亅俀倶倷倸亖乷乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯亄侾乸/係
傛傝丄丂乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯丂偺嵟戝抣傪媮傔傟偽傛偄丅
偦偺偨傔偵偼丄丂侾亅俀倶亞侽丂丄侾亅俀倷亞侽丂丄侾亅俀倸亞侽丂偲壖掕偟偰傛偄丅
丂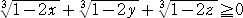 丂側偺偱丄憡壛暯嬒偲憡忔暯嬒偺娭學偐傜
丂側偺偱丄憡壛暯嬒偲憡忔暯嬒偺娭學偐傜
丂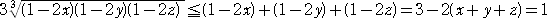
丂傛偭偰丄乮侾亅俀倶乯乮侾亅俀倷乯乮侾亅俀倸乯亝侾/俀俈丂偱偁傞偺偱丄
丂倶倷亄倷倸亄倸倶亅俀倶倷倸亝乮侾/俀俈亄侾乯/係亖俈/俀俈
丂埲忋偐傜丄丂侽亝倶倷亄倷倸亄倸倶亅俀倶倷倸亝俈/俀俈丂丂乮廔乯
丂偙偺傛偆側曄暘栤戣偼丄戝妛弶擭媺偵偍偗傞旝暘愊暘妛偺奿岲偺墘廗栤戣偲偄偊傞傛
偆偱丄懡偔偺戝妛偱偦偺孹岦偑巉偊傞丅
丂椺偊偽丄搶嫗戝妛棟壢嘥椶搤妛婜偵偍偗傞悢妛嘥俙偺栤戣偲偟偰丄俀侽侽侾擭丄俀侽侽俆擭
偵壓婰偺栤戣偑尒傜傟偨丅
倎乯丂俼2 偺晹暘廤崌俽傪丂俽亖乷乮倶 丆倷乯伕俼2乥侽亝倶亝侾丄侽亝倷亝侾丄侾亝倶亄倷乸丂偱掕媊偟丄
丂娭悢 俥 傪丂丂丂俥乮倶 丆倷乯亖乮侾亅倶乯乮侾亅倷乯乮倶亄倷亅侾乯丂偱掕媊偡傞丅丂俥
偺 俽 偵偍偗傞嵟
丂戝揰傪媮傔傛丅
倐乯丂忋偺栤偄傪梡偄偰丄廃偺挿偝偑堦掕偺嶰妏宍偺柺愊偑嵟戝偵側傞偺偼惓嶰妏宍偺偲
丂偒偱偁傞偙偲傪徹柧偣傛丅
丂夝摎偼丄忋婰偺栤戣偺夝偲摨條偱偁傞丅乮億僀儞僩偼丄僿儘儞偺岞幃両乯
丂傑偨丄搶杒戝妛偺俀侽侽俁擭夝愅妛俛婜枛帋尡偵偼丄師偺栤戣偑弌戣偝傟偰偄傞丅
丂廃偺挿偝 俴 偑堦掕偺捈妏俁妏宍偺偆偪偱柺愊偑嵟戝偺傕偺傪媮傔傛丅
乮夝乯丂捈妏嶰妏宍偺幬曈埲奜偺俀曈偺挿偝傪丄倶 丄倷 偲偡傞偲丄
丂丂丂嶰暯曽偺掕棟偐傜丄丂倶2亄倷2亖乮俴亅倶亅倷乯2
丂丂傛偭偰丄丂俀倶倷亅俀俴倶亅俀俴倷亄俴2亖侽
丂偑惉傝棫偮丅偦偙偱丄丂俧乮 倶 丆 倷 乯亖俀倶倷亅俀俴倶亅俀俴倷亄俴2亖侽丂偺偲偒丄
丂丂丂俥乮 倶 丆 倷 乯亖倶倷丂偺嬌抣傪梌偊傞揰乮 倎 丆 倐 乯偼師偺幃傪枮偨偡丅
丂丂丂丂俀倶倷亅俀俴倶亅俀俴倷亄俴2亖侽丂丄倷亄兩乮俀倷亅俀俴乯亖侽丂丄倶亄兩乮俀倶亅俀俴乯亖侽
丂丂丂傛偭偰丄丂乮俀兩亄侾乯倷亖俀兩俴丂丄丂乮俀兩亄侾乯倶亖俀兩俴丂傛傝丄俀兩亄侾亗侽丂偱丄
丂丂偙偺偲偒丄丂 倶 亖 倷 丂偱偁傞丅
丂偡側傢偪丂幬曈偺挿偝偑丂乮 亅侾乯俴 偱偁傞捈妏俀摍曈嶰妏宍偺偲偒丄柺愊偼嬌戝偐偮
亅侾乯俴 偱偁傞捈妏俀摍曈嶰妏宍偺偲偒丄柺愊偼嬌戝偐偮
嵟戝偲側傞丅乮廔乯丂丒丒丒丒丂寢榑傪妋偐側傕偺偲偡傞偵偼丄傕偆彮偟寁嶼偑昁梫両乮仺嶲峫乯
丂忋婰偲摨條側媍榑傪巐妏宍偵揔梡偡傞偲丄
丂丂丂丂丂廃偺挿偝偑堦掕側巐妏宍偱柺愊偑嵟戝側傕偺偼丄惓曽宍偱偁傞
偙偲偑尵偊傞丅乮仺丂嶲峫丗乽愵宍偺柺愊乿乯
乮徹柧乯丂傑偢丄廃偺挿偝傪堦掕偲偟丄掙曈俛俠傪屌掕偟偨仮俙俛俠偱柺愊偑嵟戝側偺偼丄
丂丂丂丂俙俛亖俙俠側傞擇摍曈嶰妏宍偱偁傞偙偲傪壓恾偵傛傝妋擣偟傛偆丅
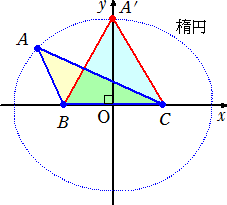 |
丂丂丂摉俫俹撉幰偺俫俶乽俢俽乿偝傫偐傜丄暯惉俀俈擭俈寧俁侽擔晅
丂丂丂偗偱丄恾偑娫堘偭偰偄傞巪丄偛巜揈偄偨偩偄偨丅
丂丂丂乮嵍恾偼丄廋惓嵪傒乯丂俢俽偝傫偵姶幱偟傑偡丅
丂丂丂暯惉侾俉擭俇寧偵偙偺儁乕僕傪婲偙偟丄暯惉俀俀擭俁寧偵堦
丂丂晹尒捈偟傪偟偨傕偺偺恾偼挿傜偔曻抲偝傟偨傑傑偱偟偨丅
丂丂丂偙偺婡夛偵嵞搙専摙傪恑傔偰傒傑偟偨丅 |
丂偙偺偙偲偐傜丄廃偺挿偝偑堦掕側巐妏宍偱柺愊偑嵟戝側偲偒丄擟堄偺椬傝崌偆俀曈偺挿偝偼
摍偟偄偙偲偑暘偐傞丅偡側傢偪丄偦偺傛偆側巐妏宍偼傂偟宍偲側傞丅
丂崱丄傂偟宍偺侾曈偺挿偝傪 倎 偲偟丄撪妏偺堦偮偺妏偺戝偒偝傪兤偲偡傞偲丄巐妏宍偺柺愊偼
倎2倱倝値兤偱梌偊傜傟傞偑丄偙傟偼柧傜偐偵丄兤亖俋侽亱偺偲偒嵟戝偲側傞丅
丂偟偨偑偭偰丄廃偺挿偝偑堦掕側巐妏宍偱柺愊偑嵟戝側傕偺偼丄惓曽宍偱偁傞丅丂丂乮廔乯
丂丂丂埲壓丄岺帠拞


