最近次のようなことを発見して少し驚きました。
「周が一定の扇形で面積が最大になるのは?」という問題で、解く事は難しくありません。
周の長さを L とすると、半径が L/4、中心角が 2(rad)のときに、面積は、最大値 L2/16
になります。
実際に、 扇形の半径を r 、中心角をθとすると、 2r+rθ=L で、面積 S は、
S=(1/2)r2θ=(1/2)r(L−2r)=−r2+(1/2)rL=−(r−L/4)2+L2/16
より、 r=L/4 のとき最大で、最大値 L2/16 をとる。
一方、周の長さが L の四角形では、正方形になるときに面積が最大で、最大値 L2/16
です。
同じ周長で、扇形と四角形の面積をそれぞれ最大化すると、等しい面積になる。しかも、
そのとき、扇形の半径の部分と正方形の一辺がぴったりと重なる、ということに不思議さを
感じずにいられない。何か数学的な意味があることなのだろうか。
FNさんからのコメントです。(平成22年5月28日付け)
確かにそうなりますね。びっくりしました。数学的な意味となるとわかりませんが、四角形
でなく長方形として、長方形と扇形で考えると式のレベルで言えば次のように同じ式になり
ますね。
長方形 2辺を x、y とすると、 2x+2y=L のもとで、S=xy を最大にせよ。
扇形 半径を x、弧の長さを 2y とすると、中心角は、2y/x だから、面積Sは、
S=(1/2)x2・2y/x=xy となる。
よって、長方形の場合と同じで、
「2x+2y=L のもとで、S=xy を最大にせよ。」
となる。
(補足) 扇形の面積を、 S=(1/2)r・l ( l は弧の長さ) で表せば、これは、2辺が r、
l/2 の長方形の面積と同じです!
らすかるさんからのコメントです。(平成22年5月28日付け)
私もその事実は知りませんでしたが、考えてみると、扇形は微小角ごとに細く切って、1個
おきに逆向きにすれば、周の長さが変わらずに長方形になりますので、「周の長さが一定の
最大面積の長方形」と同じになるのは当然といえば当然ですね。
(コメント) 遊名人さんの気づかれたことは実は昔から知られていて、FNさんの(補足)にあ
る考え方が有名です。最も、「扇形の面積=三角形の面積」という見方ですが..。
この考え方を私自身、中学3年のときに知ったのですが、そのときは遊名人さん
同様に不思議さを感じずにはいられませんでした。
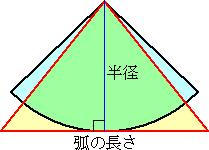
広島工業大学の大川研究室よりアドバイスをいただきました。(平成22年6月20日付け)
上図の「扇形の面積=三角形の面積」という見方の背景には、次の定理が存在する。
xy-平面に、面積を持つ二つの図形 A, B があるとする。但し、 A は、xy-平面の
x > 0 の部分 に有るとする。任意の正の実数 a > 0 に対し、 A と直線 x=a の
交わりの長さと、B と原点中心の半径 a の円周の交わりの長さが等しいとき、A の
面積と B の面積は等しい。 (→ 参考:大川研究室 数学の問題414)
(注意) x ≧ 0、 a ≧ 0 としても同様である。
(証明) 変換 ( x , y ) → ( x・cos(y/x) , x・sin(y/x) ) を考える。
これは、直線 x=a を円周 x2+y2=a2 に接点と長さを保ちながらねじ曲げる(巻き付
ける)変換である。この変換の Jacobian が恒等的に 1 なる変換である事は簡単な計
算で分かる。実際に、
u=x・cos(y/x) 、 v=x・sin(y/x) に対して、
ux=cos(y/x)+(y/x)sin(y/x)
uy=−sin(y/x)
vx=sin(y/x)−(y/x)cos(y/x)
vy=cos(y/x)
なので、 ux・vy−uy・vx=cos2(y/x)+sin2(y/x)=1 より明らか。
これは 1対1 の変換ではないが、定義域・値域を適当に設定する事により逆変換も定
義でき、その Jacobian も恒等的に 1 なので、面積を変えない。 (証終)
