カークマンの組分け 
15人を、3人ずつ、5班に分ける方法の数を求めることは、順列・組合せにおける標準的な
問題である。実際に、
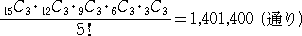
ある。ところで、上の問題に対して、1度同じ班になった人とは2度と同じ班にならないと仮定
するような場合の方が、実生活でよく直面する。
たとえば、6チームのリーグ戦(総当り戦)で、同時に3試合ずつ5回戦を行う場合とか...。
1847年に、Kirkman(1806〜1895)は、次のような問題を提出している。
(正式な名前は、「カークマンの女生徒の問題」という。女生徒というのは、問題に対して本
質的ではないと思うのだが、なぜか、カークマンは「女生徒」と限定している!?)
15人を、次のように班分けする。
1日目・・・15人を、3人ずつ、5班に分ける。
2日目・・・15人を、3人ずつ、5班に分ける。ただし、1度同じ班になった人とは2度と同じ班
にならないものとする。
3日目・・・2日目と同様の条件で、15人を、3人ずつ、5班に分ける。
4日目、5日目、6日目、7日目も、2日目と同様の条件で、15人を、3人ずつ、5班に分ける。
このとき、どんな班分けになるだろうか?
これに対して、次のような班分けが知られている。(生徒を、1、2、3、・・・、15
で表す。)
| 1日目 |
1 2 5 |
3 4 7 |
6 8 14 |
9 10 13 |
11 12 15 |
| 2日目 |
1 3 9 |
2 8 15 |
4 11 13 |
5 12 14 |
6 7 10 |
| 3日目 |
1 4 15 |
2 13 14 |
3 10 12 |
5 6 9 |
7 8 11 |
| 4日目 |
1 6 11 |
2 7 12 |
3 8 13 |
4 9 14 |
5 10 15 |
| 5日目 |
1 7 14 |
2 4 10 |
3 5 11 |
6 13 15 |
8 9 12 |
| 6日目 |
1 8 10 |
2 9 11 |
3 14 15 |
4 6 12 |
5 7 13 |
| 7日目 |
1 12 13 |
2 3 6 |
4 5 8 |
7 9 15 |
10 11 14 |
| 1日目 |
1 2 8 |
3 5 13 |
4 7 9 |
6 10 15 |
11 12 14 |
| 2日目 |
1 3 11 |
2 5 14 |
4 8 15 |
6 7 13 |
9 10 12 |
| 3日目 |
1 4 13 |
2 7 10 |
3 14 15 |
5 6 12 |
8 9 11 |
| 4日目 |
1 5 10 |
2 3 9 |
4 6 14 |
7 11 15 |
8 12 13 |
| 5日目 |
1 6 9 |
2 13 15 |
3 7 12 |
4 5 11 |
8 10 14 |
| 6日目 |
1 7 14 |
2 4 12 |
3 6 8 |
5 9 15 |
10 11 13 |
| 7日目 |
1 12 15 |
2 6 11 |
3 4 10 |
5 7 8 |
9 13 14 |
班分けの方法は、上記以外にも、たくさんある!
はたして、このような班分けは、どのような考え方をすれば求められるのだろうか? いくつか
簡単な場合について検討し、考察することにしよう。
例 番号1、2、3、4、5、6 の6人が、リーグ戦(総当り戦)を行う。同時に3試合ずつ5回戦を
行う場合、どのように試合の順番を決めればよいか?
表を作って求めてみよう。(1〜5回戦を、記号 A〜E で表す。)
|
解の例1 |
|
解の例2 |
| |
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
・ |
A |
B |
C |
D |
E |
| 2 |
A |
・ |
E |
D |
B |
C |
| 3 |
B |
E |
・ |
A |
C |
D |
| 4 |
C |
D |
A |
・ |
E |
B |
| 5 |
D |
B |
C |
E |
・ |
A |
| 6 |
E |
C |
D |
B |
A |
・ |
|
|
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
・ |
A |
B |
C |
D |
E |
| 2 |
A |
・ |
D |
B |
E |
C |
| 3 |
B |
D |
・ |
E |
C |
A |
| 4 |
C |
B |
E |
・ |
A |
D |
| 5 |
D |
E |
C |
A |
・ |
B |
| 6 |
E |
C |
A |
D |
B |
・ |
|
解は、上記以外にも、たくさん作ることができる。
上記の問題に対して、次のような素晴らしいアイデアがあることを最近知った。
(参考文献:ホームページ:「未菜実の数理パズル入門」の「リーグ戦の組合せ」)
まず分かっていることは、番号1 は、番号2〜6 と 1 回だけ対戦するということ、そして、
隣り合う番号同士の対戦には限界があり、番号一つ飛ばしの対戦も適当に織り交ぜなけ
ればならないということである。
そこで、次のような円を考え、中心には、番号1を配置し、円周の5等分点上に、番号2
〜6を配置する。
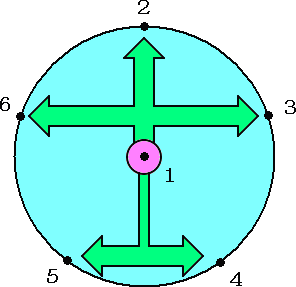
上の図で、緑色の針を時計回りに72度ずつ回転させれば、解の例2にあるような対戦方法
を得ることができる。
解の特徴から、番号2〜6 の円順列を考えることにより、このパターンの解は、24通りある
ことが分かる。しかしながら、解の例 1 が存在することからも分かるように、このアイデアによ
り、この問題に対する解が全て得られるわけではないということに注意しなければならない。
ただ、この方法を知っていれば、人数が比較的多い場合でも、解の一つが、同様に簡便に
求められるという点で優れている。
例 番号1、2、・・・16 の16人が、リーグ戦(総当り戦)を行う。同時に8試合ずつ15回戦を
行う場合、どのように試合の順番を決めればよいか?
この問題を試行錯誤で求めることは、至難の業でしょう。アイデアを使うと、簡単に求められる。
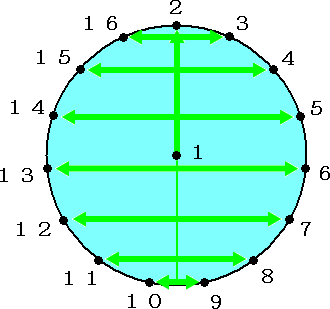
上と同様に、1〜15回戦を、記号 A〜O で表すとすると、解の一つとして、次の組合せが考
えられる。
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 1 |
・ |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| 2 |
A |
・ |
I |
B |
J |
C |
K |
D |
L |
E |
M |
F |
N |
G |
O |
H |
| 3 |
B |
I |
・ |
J |
C |
K |
D |
L |
E |
M |
F |
N |
G |
O |
H |
A |
| 4 |
C |
B |
J |
・ |
K |
D |
L |
E |
M |
F |
N |
G |
O |
H |
A |
I |
| 5 |
D |
J |
C |
K |
・ |
L |
E |
M |
F |
N |
G |
O |
H |
A |
I |
B |
| 6 |
E |
C |
K |
D |
L |
・ |
M |
F |
N |
G |
O |
H |
A |
I |
B |
J |
| 7 |
F |
K |
D |
L |
E |
M |
・ |
N |
G |
O |
H |
A |
I |
B |
J |
C |
| 8 |
G |
D |
L |
E |
M |
F |
N |
・ |
O |
H |
A |
I |
B |
J |
C |
K |
| 9 |
H |
L |
E |
M |
F |
N |
G |
O |
・ |
A |
I |
B |
J |
C |
K |
D |
| 10 |
I |
E |
M |
F |
N |
G |
O |
H |
A |
・ |
B |
J |
C |
K |
D |
L |
| 11 |
J |
M |
F |
N |
G |
O |
H |
A |
I |
B |
・ |
C |
K |
D |
L |
E |
| 12 |
K |
F |
N |
G |
O |
H |
A |
I |
B |
J |
C |
・ |
D |
L |
E |
M |
| 13 |
L |
N |
G |
O |
H |
A |
I |
B |
J |
C |
K |
D |
・ |
E |
M |
F |
| 14 |
M |
G |
O |
H |
A |
I |
B |
J |
C |
K |
D |
L |
E |
・ |
F |
N |
| 15 |
N |
O |
H |
A |
I |
B |
J |
C |
K |
D |
L |
E |
M |
F |
・ |
G |
| 16 |
O |
H |
A |
I |
B |
J |
C |
K |
D |
L |
E |
M |
F |
N |
G |
・ |
上のアイデアを用いて、カークマンの女生徒の問題を解こうとしたが、なかなか上手い図が
見つからない。現在、検討中である。
(追記)
ホームページ「数学の部屋」の「3人ゲームのリーグ戦」によれば、次のような図形が求める
ものの一つの例になるらしい。
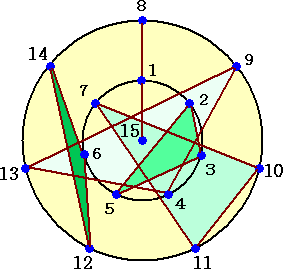
作り方のポイントは、同一円上の弦同士が、回転しても重ならないように配置するところで
ある。後は、上の図を、数字は固定したままで、1/7周ずつ回転させれば、求める解の一つ
を得ることができる。
代数学的にも、カークマンの女生徒の問題は、興味ある問題のようだ。
(有限体GF(24)を、素体GF(2)上の4次元ベクトル空間と考えて、その中の35の平面を、
5平面ずつの7組に分ける(但し、5平面の和集合は、GF(24))問題と同じである。)
(参考文献:山本幸一 著 カークマンの女生徒の問題―数学100の問題― (日本評論社))
(追々記) 上記で、「カークマンの女生徒の問題」は一応決着をみた訳であるが、最近運動部
の顧問の方から、次のような問題提起がなされた。
番号1、2、3、4、5、6 の6チームが、リーグ戦(総当り戦)を行う。ただし、同時に可能な
試合は、2試合で、残りの2チームでそれぞれの試合の審判を担当させたい。もっとも能率
的に運営するには、どのように試合の順番を決めればよいのだろうか?
6チームのリーグ戦なので、試合数は、15試合である。この15試合を、6チームで担当
するので、1チーム当たりの審判回数は、2〜3回である。チームによって、審判回数に差
が出ることを了解すれば、次のように試合の順番を決めればよいだろう。

上の図で、緑色の針を時計回りに72度ずつ回転させる。まず、「5−4」の矢印に対応する
チームを審判とし、次の回転で「2−1」の矢印に対応するチームを審判とする。この操作を
繰り返し続け、緑色の針を2回転させる。このとき、次の表を得る。
|
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
・ |
A F |
B G |
C H |
D I |
E J |
| 2 |
A F |
・ |
D I |
B G |
E J |
C H |
| 3 |
B G |
D I |
・ |
E J |
C H |
A F |
| 4 |
C H |
B G |
E J |
・ |
A F |
D I |
| 5 |
D I |
E J |
C H |
A F |
・ |
B G |
| 6 |
E J |
C H |
A F |
D I |
B G |
・ |
|
上記の表から、2度目の対戦となる場合、およびそれに付随する審判を除くことにより、次
のような試合の運営方法の一例ができる。
|
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
・ |
A |
B G |
C |
D I |
E |
| 2 |
A F |
・ |
D I |
B |
E |
C H |
| 3 |
B G |
D |
・ |
EJ |
C |
A |
| 4 |
C H |
B |
E J |
・ |
A F |
D |
| 5 |
D I |
E |
C |
A F |
・ |
B |
| 6 |
E J |
C H |
A |
D |
B G |
・ |
|
上記の表の問題点は、若干の無駄があるというところである。試合も後半になれば、疲れ
が出て、1試合ずつ消化する方が健康的かもしれないが、問題を数学的にとらえれば、この
ことは、「能率的」という意味からは許されないことである。
上記の表を更に工夫すれば、次の表が最善の表となるであろう。
|
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
・ |
A |
B F |
C |
D G |
E |
| 2 |
A F |
・ |
D G |
B |
E |
C H |
| 3 |
B F |
D |
・ |
E G |
C |
A |
| 4 |
C H |
B |
E G |
・ |
A F |
D |
| 5 |
D G |
E |
C |
A F |
・ |
B |
| 6 |
E G |
C H |
A |
D |
B F |
・ |
|
A ・・・ 1回戦(2試合)
B ・・・ 2回戦(2試合)
C ・・・ 3回戦(2試合)
D ・・・ 4回戦(2試合)
E ・・・ 5回戦(2試合)
F ・・・ 6回戦(2試合)
G ・・・ 7回戦(2試合)
H ・・・ 8回戦(1試合)
黒字は、試合をする組
赤字は、審判をする組
ただし、表は横方向にみる
ことにする。
|
上記の表では、残念ながら、3試合連続となる場合が含まれている。生徒の負担を考え
れば、せいぜい連続する試合数は、2までとしたいのだが、これは数学的に考えて、可能
なのであろうか?直感的には、3と5が互いに素なので、多分不可能だと思うのだが、そこ
ら辺のところは、今後の研究課題としておこう。もし、証明が出来た方、こちらまで、メール
にてご教示下さい。
以上、このような表が、高体連や高文連などの専門委員の方に使われることを希望して、
筆をおくことにする。
(追記) 平成30年2月3日付け
当HPの投稿「班編成」で、カークマンの組分けに類似した問題が議論された。当HPがい
つもお世話になっているHN「GAI」さんが、らすかるさんの一気に条件を満たす組み合わせ
を構成されているのに衝撃を受けられたとのことで、らすかるさんのやり方をカークマンの
女学生問題:
15人を3人ずつの5班に分け散歩する。これを一週間続けたら、どの人も他の人と
散歩を共にしたことが起こった。
というものに応用された。
解答のいくつかの組み合わせ(7通りあるらしい。)がネット等に出ていたので、この解を
参考に逆に構成方法を探ってみた。
まず、3人の班が全部で 5*7=35 組作られて、この35組の組み合わせからどの人も他の
人と出会えるメンバーを決めていかないといけない。(ここが最も難所)
ここを、らすかるさんのテクニックを利用して、1〜15の各数に
A:(+0,+1,+12) ,B:(+0,+2,+9) ,C:(+0,+5,+10) の3グループに分ける。(ただし結果はソートしている)
1->[1,2,13] ,[1,3,10]
,[1,6,11]
2->[2,3,14] ,[2,4,11]
,[2,7,12]
3->[3,4,15] ,[3,5,12]
,[3,8,13]
4->[1,4,5] ,[4,6,13]
,[4,9,14]
5->[2,5,6] ,[5,7,14]
,[5,10,15]
6->[3,6,7] ,[6,8,15]
,[1,6,11]
7->[4,7,8] ,[1,7,9] ,[2,7,12]
8->[5,8,9] ,[2,8,10]
,[3,8,13]
9->[6,9,10] ,[3,9,11]
,[4,9,14]
10->[7,10,11] ,[4,10,12] ,[5,10,15]
11->[8,11,12] ,[5,11,13] ,[1,6,11]
12->[9,12,13] ,[6,12,14] ,[2,7,12]
13->[10,13,14] ,[7,13,15] ,[3,8,13]
14->[11,14,15] ,[1,8,14] ,[4,9,14]
15->[1,12,15] ,[2,9,15] ,[5,10,15]
実は、Aグループを導き出せるのは他にも
(+0,+3,+4)、(+0,+11,+14)、(+1,+2,+13)、(+1,+4,+5)、(+2,+3,+14)、(+2,+5,+6)、(+3,+6,+7)
(+4,+7,+8)、(+5,+8,+9)、(+6,+9,+10)、(+7,+10,+11)、(+8,+11,+12)、(+9,+12,+13)、(+10,+13,+14)
同じくBグループでは、
(+0,+6,+8)、(+0,+7,+13)、(+1,+3,+10)、(+1,+7,+9)、(+1,+8,+14)、(+2,+4,+11)、(+2,+8,+10)
(+3,+5,+12)、(+3,+9,+11)、(+4,+6,+13)、(+4,+10,+12)、(+4,+10,+12)、(+5,+7,+14)、(+5,+11,+13)
(+6,+12,+14)
Cグループでは、
(+1,+6,+11)、(+2,+7,+12)、(+3,+8,+13)、(+4,+9,+14)
でも可能ですが、最も計算上楽なものを選んでいます。こうして導き出せた35通りの組合せ:
[1,2,13]、[1,3,10]、[1,4,5]、[1,6,11]、[1,7,9]、[1,8,14]、[1,12,15]、[2,3,14]、[2,4,11]、[2,5,6]、[2,7,12]
[2,8,10]、[2,9,15]、[3,4,15]、[3,5,12]、[3,6,7]、[3,8,13]、[3,9,11]、[4,6,13]、[4,7,8]、[4,9,14]、[4,10,12]
[5,7,14]、[5,8,9]、[5,10,15]、[5,11,13]、[6,8,15]、[6,9,10]、[6,12,14]、[7,10,11]、[7,13,15]、[8,11,12]
[9,12,13]、[10,13,14]、[11,14,15]
これらは各数字が7回ずつ出現しており、相互関係を調べてみれば、お互い他のメンバー
とピタリ一度は行動を共に出来ることができる組合せの組み合わせが出来ていることが確認
できます。
後は、これを7行5列に並べ、各行が1〜15のメンバーを含むようにナンプレよろしく配置し
ていく。
G1: G2: G3: G4: G5:
[1,2,13] [3,6,7] [4,10,12] [5,8,9] [11,14,15]
[1,3,10] [2,5,6] [4,9,14] [7,13,15] [8,11,12]
[1,4,5] [2,3,14] [6,8,15] [7,10,11] [9,12,13]
[1,6,11] [2,9,15] [3,5,12] [4,7,8] [10,13,14]
[1,7,9] [2,4,11] [3,8,13] [5,10,15] [6,12,14]
[1,8,14] [2,7,12] [3,4,15] [5,11,13] [6,9,10]
[1,12,15] [2,8,10] [3,9,11] [4,6,13] [5,7,14]
これで当初の目的が達成できる。
「班分けの妙」と題して、当HPがいつもお世話になっているHN「GAI」さんよりご投稿いた
だきました。(平成30年3月6日付け)
カークマンの問題から興味が出て、「組合せ理論」(ホール著)を勉強してみたら、ブロック・
デザインの作り方がいろいろ紹介されていて、この本に書いてある誘導に従い、実験を繰り
返し試みてみると、いろいろなパターンが作れていくことがわかりました。
(何故可能かの証明は難しくて分かりませんが・・・)
この中で、同じ15人をいろいろな目的で班分けしてみることが可能であることができました。
本ではいろいろな記述方法を使ってあったので、15人の参加者は、1,2,3,・・・,15の数字に置
き換え、また班はソートしたもので統一的に表示しています。
v:参加人数
b:班分け(ブロック)総数
r:各人の参加回数
k:班分け人員数
λ:各自が他のメンバーと出会う回数
<その1> (v,b,r,k,λ)=(15,35,7,3,1)
*これを一日に5班ずつ上手く組み合わせて7日間散歩させるものがカークマンの女学生問題
(班)
1 1 2 5
2 1 3 10
3 1 4 15
4 1 6 11
5 1 7 9
6 1 8 14
7 1 12 13
8 2 3 6
9 2 4 11
10 2 7 12 |
|
11 2 8 10
12 2 9 15
13 2 13 14
14 3 4 7
15 3 5 12
16 3 8 13
17 3 9 11
18 3 14 15
19 4 5 8
20 4 6 13 |
|
21 4 9 14
22 4 10 12
23 5 6 9
24 5 7 14
25 5 10 15
26 5 11 13
27 6 7 10
28 6 8 15
29 6 12 14
30 7 8 11 |
|
31 7 13 15
32 8 9 12
33 9 10 13
34 10 11 14
35 11 12 15 |
< その2> (v,b,r,k,λ)=(15,15,7,7,3)
1 1 2 3 4 5 6 7
2 1 2 3 8 9 10 11
3 1 2 3 12 13 14 15
4 1 4 5 8 9 12 13
5 1 4 5 10 11 14 15
6 1 6 7 8 9 14 15
7 1 6 7 10 11 12 13
8 2 4 6 8 10 12 14
9 2 4 7 8 11 13 15
10 2 5 6 9 11 12 15 |
|
11 2 5 7 9 10 13 14
12 3 4 6 9 11 13 14
13 3 4 7 9 10 12 15
14 3 5 6 8 10 13 15
15 3 5 7 8 11 12 14 |
< その3> (v,b,r,k,λ)=(15,42,14,5,4)
1 1 2 3 4 5
2 1 2 4 9 13
3 1 2 6 8 11
4 1 2 8 14 15
5 1 3 4 6 15
6 1 3 5 8 12
7 1 3 6 11 12
8 1 4 9 14 15
9 1 5 7 10 15
10 1 5 7 13 14
11 1 6 7 11 13
12 1 7 9 10 12
13 1 8 9 10 12
14 1 10 11 13 14 |
|
15 2 3 5 10 14
16 2 3 7 9 12
17 2 3 9 11 15
18 2 4 5 7 11
19 2 4 7 12 13
20 2 5 10 11 15
21 2 6 12 14 15
22 2 6 8 10 13
23 2 6 9 10 13
24 2 7 8 12 14
25 3 7 11 13 15
26 3 4 8 10 13
27 3 4 10 11 12
28 3 5 8 13 14 |
|
29 3 6 7 9 14
30 3 6 7 10 14
31 3 8 9 13 15
32 4 5 6 9 14
33 4 5 6 12 13
34 4 6 7 8 15
35 4 7 8 10 15
36 4 8 11 12 14
37 4 9 10 11 14
38 5 6 8 9 11
39 5 6 10 12 15
40 5 7 8 9 11
41 5 9 12 13 15
42 11 12 13 14 15 |
< その4> (v,b,r,k,λ)=(15,35,14,6,5)
1 1 2 3 6 7 14
2 1 2 4 6 10 15
3 1 2 4 8 9 11
4 1 2 5 10 12 13
5 1 2 7 11 13 15
6 1 3 4 7 12 14
7 1 3 4 9 13 15
8 1 3 5 6 11 15
9 1 3 7 8 10 14
10 1 4 5 12 13 14
11 1 5 6 8 12 13
12 1 5 7 9 10 15 |
|
13 1 6 8 9 11 12
14 1 8 9 10 11 14
15 2 3 4 5 8 9
16 2 3 5 6 9 14
17 2 3 5 9 10 12
18 2 3 10 11 12 13
19 2 4 5 7 8 11
20 2 4 8 13 14 15
21 2 6 7 9 13 14
22 2 6 11 12 14 15
23 2 7 8 10 12 15
24 3 4 6 8 12 15 |
|
25 3 4 6 10 11 13
26 3 5 7 8 13 15
27 3 7 9 11 12 15
28 3 8 10 11 13 14
29 4 5 6 7 10 11
30 4 5 7 9 10 13
31 4 6 7 11 12 14
32 4 9 10 12 14 15
33 5 6 8 10 14 15
34 5 9 11 13 14 15
35 6 7 8 9 12 13 |
なお、λ=2 ((v,b,r,k,λ)=(15,21,7,5,2))は不可能であるとのこと。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月7日付け)
以下のような理解でよろしいでしょうか。
(v,b,r,k,λ)=(6,10,5,3,2)
1 2 3
1 2 4
1 3 5
1 4 6
1 5 6
2 3 6
2 4 5
2 5 6
3 4 5
3 4 6
#λが2だとキツいです……。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月7日付け)
Figure 9. The 15 planes and 35 lines of the smallest projective space.
(リンクされたページは、ノートン様より「危険なページ」とご指摘を受けたので割愛)
15人の女学生のそれぞれに Fano plane を与えます。Figure 9 の上半分です。
Figure 9 の下半分には、35の line があるのですが、 ひとつの line 、例えば 3,10,11 を持
つ Fano plane は 3 個あるようです。
共通の line を有する Fano plane を与えられた 3 人の女学生がひとつの班を組むことと
すると、班はlineで特徴つけられます。
すごく面白く不可思議です。
GAIさんからのコメントです。(平成30年3月7日付け)
ハンニバル・フォーチュンさん、お見事です。では、(v,b,r,k,λ)=(7,14,6,3,2)に挑戦してみて
下さい。ただし、14回の班構成は同じメンバーが何度でも組合わせられることも許すものと
します。
また、出会いを一つ増やし、(v,b,r,k,λ)=(8,14,7,4,3)なる班編成にも挑戦を!
(この場合は班のメンバーはすべて異なるようにして下さい。)
DD++さんからのコメントです。(平成30年3月7日付け)
前半は、(v,b,r,k,λ)=(7,7,3,3,1) が解けるので同じグループを2回作る解があるのはわかる
として、後半って、仮に同じグループを作ることを許容したらそういう解も作れるんですかね?
あんまりできそうな印象を受けませんが……。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月7日付け)
(v,b,r,k,λ)=(8,14,7,4,3) についてです。まず、ファノ平面をひとつ用意します。
{1,2,3}
{1,4,5}
{1,6,7}
{2,4,6}
{2,5,7}
{3,4,7}
{3,5,6}
どの line=班 にも 8 を参加させます。すなわち、
{1,2,3,8}
{1,4,5,8}
{1,6,7,8}
{2,4,6,8}
{2,5,7,8}
{3,4,7,8}
{3,5,6,8}
{1,2,3,4,5,6,7,8} に対しての補集合を右隣に書きます。
{1,2,3,8} {4,5,6,7}
{1,4,5,8} {2,3,6,7}
{1,6,7,8} {2,3,4,5}
{2,4,6,8} {1,3,5,7}
{2,5,7,8} {1,3,4,6}
{3,4,7,8} {1,2,5,6}
{3,5,6,8} {1,2,4,7}
以上で、作れた気がいたします。
今度は、(v,b,r,k,λ)=(7,14,6,3,2) についてです。第一のファノ平面を以下のように用意しま
す。
{1,2,3}
{1,4,5}
{1,6,7}
{2,4,6}
{2,5,7}
{3,4,7}
{3,5,6}
上記のように、ファノ平面は7本の line からなり、各 line は3点からなるわけですが、上記
では、各 line の点の番号を二進三桁にして 3点の排他的論理和をとると、いずれも 000 と
なっています。
ついで、第二のファノ平面を以下のように用意します。
{3,4,6}
{1,5,6}
{2,6,7}
{2,3,5}
{1,3,7}
{4,5,7}
{1,2,4}
上記では、各 line の点の番号を二進三桁にして 3点の排他的論理和をとると、順に 001
から 111 までが出現しています。
※その心は、第一のファノ平面と第二のファノ平面とで、 line がかぶらない、というわけです。
第一のファノ平面と第二のファノ平面との line を マージします。
{1,2,3}
{1,4,5}
{1,6,7}
{2,4,6}
{2,5,7}
{3,4,7}
{3,5,6}
{3,4,6}
{1,5,6}
{2,6,7}
{2,3,5}
{1,3,7}
{4,5,7}
{1,2,4}
昇順に整理して
{1,2,3}
{1,2,4}
{1,3,7}
{1,4,5}
{1,5,6}
{1,6,7}
{2,3,5}
{2,4,6}
{2,5,7}
{2,6,7}
{3,4,6}
{3,4,7}
{3,5,6}
{4,5,7}
これが求める(v,b,r,k,λ)=(7,14,6,3,2)の一例になっていると思います。
DD++さんからのコメントです。(平成30年3月7日付け)
(v,b,r,k,λ)=(8,14,7,4,3)について、ハンニバルさんとは違う方法を。
立方体の頂点に8人を配置します。立方体の4頂点の組のうち、正四面体を構成できるも
のが2組、同一平面上にあるものが12組あり、その計14組で条件を達成できます。
落ち着いて考えたらもっと単純でした。
8人に3桁の二進数で000から111までの番号をつけます。4人の排他的論理和が000になる
組が14組あるのでそれを採用しておしまい、ですね。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月8日付け)
DD++さん、素晴らしいです!
==以下雑談です==
DD++さんからの御考察からインスピレーションをいただきまして、切頂四面体の絵をご覧
ください。これが一番説明に都合が良いのですが。
ここでは、正四面体の頂点付近を切り飛ばして、もとの正四面体の面が正六角形になって
いる、とお考えください。
正六角形に内接する円を描けばトータルで4つあります。これらの円が互いに接する点は、
計6点あります。
さらに、切頂四面体の重心がひとつありますので、これを7点めとします。この7点がファノ
平面を構成しうる、というオハナシになります。
さきほどの通り、4つ円が互いに接する点は、計6点あります。次に述べる基準で、6点は
2点づつの3組にわけることができます。
【重心をはさんで正反対側にいる点どうしをペアとする】
ペアどうしを結んで3本の線分を描けば、これらは互いに直交します。いまつくった3本の
各線分には、今注目している7点のうち3点がのっています。
ファノ平面を構成する7本のLINEのうち3本が、いまできた、と考えます。
ファノ平面を構成する7本のLINEのうち残りの4本がどこにあるかというと、《正六角形に
内接する円を描けばトータルで4つありま》したが、各円には3つの点がのっているのでした。
つまり、円もまたLINEです。
以上で、7本のLINEが構成されたのですが……、このファノ平面の立体図解は私がつくっ
たのではなくてエライ人がつくったわけでして、単にご案内していることになります。
DD++さんによる立方体の図解が非常に興味深く、思わず反応してしまいました。あとでよ
く考えてみたいのですけれども、切頂四面体の絵では右端に、切頂四面体が立方体に埋め
込まれています。
なにかオモロイことでもみつからないかと思っています。【根拠なしです】
DD++さんからのコメントです。(平成30年3月8日付け)
切頂四面体なんて用意しなくても、正八面体でいいんじゃないでしょうか。
正八面体の頂点と中心に7人を配置し、各面の頂点3人組で8つ、正八面体の対角線を
3つ×2回ずつで、(v,b,r,k,λ)=(7,14,6,3,2) の解になります。
あるいは、正八面体を隣り合う面が異なる色になるよう二色に塗り分け、片方の色の面
の頂点3人組で4つ、正八面体の対角線3つで、(v,b,r,k,λ)=(7,7,3,3,1) の解になります。
採用する片方の色の面に外接円でも書いておけば、ハンニバルさんのやりたいことは達
せられるんじゃないかと思いますがいかがでしょう?
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月8日付け)
いろいろな素敵なアイデアを有難うございます。7人から1人ふやしてなお うまくいく、 これ
が当然と思えるような図解が欲しかったのでした。
「カークマン女学生麻雀大会」と題して、GAIさんからの出題です。(平成30年3月9日付け)
16人の女学生がマージャン大会を企画し、雀卓を4台準備し適当に4班に分けてそれぞれ
の卓で腕を競い合った。
次の日も同様に4班に分かれて競った。(ただし班の構成は前回とは異なる組み合わせと
する。)
これを5日間繰り返した時、どの女学生も他のメンバーと面子を組むことになっていたとい
う。さてこの班の構成はいかなるものであったのか?
(これは、(v,b,r,k,λ)=(16,20,5,4,1)のブロック・デザインを構成することに対応する。)
これが上手く作れたら、(v,b,r,k,λ)=(28,63,9,4,1)、(v,b,r,k,λ)=(40,130,13,4,1)の構成方法の
アイデアを編み出してほしい。
DD++さんからのコメントです。(平成30年3月9日付け)
(解法1) A:0から4、B:0から4、C:0から4、D で命名し、k日目は、
A:k と B:k と C:k と D
A:k±1 と B:k±2
B:k±1 と C:k±2
C:k±1 と A:k±2
の4つの卓を作ります。(ただしmod5)
中心と3つの同心円に16人を配置し、1本の直線と3つの等脚台形を書くイメージ。あるいは
円錐でもいいですが。
(解法2) 以下で = は ≡ (mod2) を意味するものとします。
二次方程式 x^2+x+1=0 の解の片方をαと表記することにします。(もちろん普通には解が
ないので、虚数単位の定義みたいな感じで)
係数が0と合同であれば、2α=0 のようにできるとすれば、もう片方の解は α+1 になりま
す。これは α^2 にも等しい数です。
x座標が 0,1,α,1+α のいずれか、y座標もこれらのいずれか、という全16個の点に人を並
べます。
1日目・・・(0,0) と (1,0) を結び、全員からこれと平行な線 y=k を引きます(mod2世界なので
閉曲線になります)同じ閉曲線上にいる人を集めると、
(0,0), (1,0), (α,0), (1+α,0) の y=0 組
(0,1), (1,1), (α,1), (1+α,1) の y=1 組
(0,α), (1,α), (α,α), (1+α,α) の y=α 組
(0,1+α), (1,1+α), (α,1+α), (1+α,1+α) の y=1+α 組
ができます。
2日目・・・(0,0) と (1,1) を結び、全員からこれと平行な線 y=x+k を引きます。同じ閉曲線上に
いる人を集めると、
(0,0), (1,1), (α,α), (1+α,1+α) の y=x 組
(0,1), (1,0), (α,1+α), (1+α,α) の y=x+1 組
(0,α), (1,1+α), (α,0), (1+α,1) の y=x+α 組
(0,1+α), (1,α), (α,1), (1+α,0) の y=x+1+α 組
ができます。
3日目・・・(0,0) と (1,α) を結び、全員からこれと平行な線 y=αx+k を引きます。同じ閉曲線
上にいる人を集めると、
(0,0), (1,α), (α,1+α), (1+α,1) の y=αx 組
(0,1), (1,1+α), (α,α), (1+α,0) の y=αx+1 組
(0,α), (1,0), (α,1), (1+α,1+α) の y=αx+α 組
(0,1+α), (1,1), (α,0), (1+α,α) の y=αx+1+α 組
ができます。
4日目・・・(0,0) と (1,1+α) を結び、全員からこれと平行な線 y=(1+α)x+k を引きます。同じ
閉曲線上にいる人を集めると、
(0,0), (1,1+α), (α,1), (1+α,α) の y=(1+α)x 組
(0,1), (1,α), (α,0), (1+α,1+α) の y=(1+α)x+1 組
(0,α), (1,1), (α,1+α), (1+α,0) の y=(1+α)x+α 組
(0,1+α), (1,0), (α,α), (1+α,1) の y=(1+α)x+1+α 組
ができます。
5日目・・・(0,0) と (0,1) を結び、全員からこれと平行な線 x=k を引きます。同じ閉曲線上にい
る人を集めると、
(0,0), (0,1), (0,α), (0,1+α) の x=0 組
(1,0), (1,1), (1,α), (1,1+α) の x=1 組
(α,0), (α,1), (α,α), (α,1+α) の x=α 組
(1+α,0), (1+α,1), (1+α,α), (1+α,1+α) の x=1+α 組
ができます。
p^mn 人が p^n 人グループを作る場合は、この(解法2)のように、mod p で既約な n 次式
を作り、その解の1つを新しい数として定義して、その n-1 次式を座標にもつm次元空間の
点を用意すればいいようです。
私の手元では、16人、52人、64人はできていても、28人と40人はまだできてないんですよ
ねえ……。
GAIさんからのコメントです。(平成30年3月10日付け)
私も、(v,b,r,k,λ)=(16,20,5,4,1)では、最初4次のアファイン平面を利用する(解法2)のやり
方で構成していましたが、慣れないせいか平行のイメージが取りにくく、作業的に時間が掛
かってしまいました。(ただし、高次元への拡張では強力な方法になりそうです。)
一方、(解法1)のやり方では、(v,b,r,k,λ)=(28,63,9,4,1)、(40,130,13,4,1)までは何とか直接的
に構成する方が楽なような気がします。
例えば、v=28(人)では、第1日目を
(A1,B1,C1,D);(A2,A3,B4,B7);(B5,B9,C6,C8);(C2,C3,A4,A7);(A5,A9,B6,B8);(B2,B3,C4,C7);(C5,C9,A6,A8)
の7班に分けて対戦させ、2日目から7日目は添え字1〜9をサイクリックに一つずつづらした
もので構成していく。(ただし9からは1へ返していく。)
v=40(人)では、第1日目では、
(A1,B1,C1,D);(A2,A3,A4,B11);(B2,B3,B4,C11);(C2,C3,C4,A11);(A5,A6,A7,B12);(B5,B6,B7,C12);
(C5,C6,C7,A12);(A8,A9,A10,B13);(B8,B9,B10,C13);(C8,C9,C10,A13)
の10班に分けて対戦させ、2日目から13日目は添え字1〜13をサイクリックに一つずつづ
らしたもので構成していく。(ただし13からは1へ返していく。)
で構成できそうです。
(v=28では添え字の離し方,v=40では班構成メンバーの組み合わせ方に苦労しました。)
DD++さんからのコメントです。(平成30年3月10日付け)
v=28(人)では、A3とB1って対戦できますかね?
v=40(人)では、A1とA4って対戦できますかね?
GAIさんからのコメントです。(平成30年3月10日付け)
ガーン!確かにλ=1の条件が達成できていませんね!(横が揃えば自動的に完成したも
のと錯覚していました。)出直します。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月10日付け)
(v,b,r,k,λ)=(28,63,9,4,1) について、私にはサッパリです。知人によれば存在は確かだとの
ことでしたので教えてもらいました。
女学生にはAからZまでの26の名のほか、αとβの名を与えます。卓の組み合わせは次
のようなものとのことでした。
1日め:HNTV FJSU GMZβ EIYα ABCD LOQX KPRW
2日め:FORV DMUX CEJP BKTβ GLWα AHQY INSZ
3日め:WXYZ DFIP BELN CHKM AGJO QRST UVαβ
4日め:GPQV COUZ FNYβ BMRα IJKL AETX DHSW
5日め:CIVX HLRU DGKN EOWβ APSα BFQZ JMTY
6日め:EMSV ANUW BHIO DJQβ FKXα CGRY LPTZ
7日め:BJVW GITU AFLM HPXβ CNQα DERZ KOSY
8日め:AKVZ BPUY CLSβ DOTα IMQW JNRX EFGH
9日め:DLVY EKQU AIRβ HJZα CFTW BGSX MNOP
構成方法については全く不明です。いくらながめてもわかりません。
GAIさんからのコメントです。(平成30年3月11日付け)
v=28(人)では、第1日目を
(A1,B1,C1,D);(A5,A6,B4,B7);(B3,B8,C2,C9);(C5,C6,A3,A8);(A2,A9,B5,B6);(B2,B9,C4,C7);(C3,C8,A4,A7)
の7班に分けて対戦させて、2日目から7日目は添え字1〜9をサイクリックに一つずつづらし
たもので構成していく。(ただし、9から1へ)
これで、λ=1の条件もクリアーできると思います。やってみてのコツは、インデックスの取り
方は2数の差を奇数1,3,5,7にする組み合わせを探す。つまり、
(5,6)->1 、(4,7)->3 、(3,8)->5 、(2,9)->7
そして、この組み合わせのインデックスをA,B,Cに行き渡らせる、の様な印象を持ちました。
(v,b,r,k,λ)=(40,130,13,4,1)の構成は、40(人)をA1〜13,B1〜13,C1〜13,とDで表すと、v=28
の場合と同様の方針を進めていき、インデックスの付け方は、
(2,13)->11 、(3,12)->9 、(4,11)->7 、(5,10)->5 、(6,9)->3 、(7,8)->1
そこで、第1日目の10班のメンバーを、
(A1,B1,C1,D);(A2,A13,B3,B12);(B5,B10,C4,C11);(C6,C9,A7,A8);(A6,A9,B4,B11);(B2,B13,C7,C8);
(C5,C10,A3,A12);(A5,A10,B7,B8);(B6,B9,C3,C12);(C2,C13,A4,A11)
で編成する。2日目から13日目まではインデックスを1つずつずらしながら班編成をする。
(ただし13からは1へ戻す。)
多分これで条件は満たされると思います。
DD++さんからのコメントです。(平成30年3月12日付け)
なるほど。A,B,C をサイクリックにするのは諦めてしまう方向になるんですね。
k±1, k±2, …… と2人ずつ差を偶数にする(mod奇数なので全部奇数にするのと実質同
じ)ところまでは行ったのですが、さらなる対称性を求めて失敗しました。
GAIさんの解をさらに考察して、k*p^n*(p^n-1)-1 人の場合全体に一般化できないか考え
てみます。
DD++さんからのコメントです。(平成30年3月7日付け)
15人から3人を選んでグループを作ることを繰り返す。ただし、一度でも一緒にグループに
入った人は、二度と一緒にグループに入らないようにするものとする。
これは、最も効率よくグループを作っていくと、35回目までグループを作ることができる。
(GAI さんの言うところの (v,b,r,k,λ)=(15,35,7,3,1) の解)
では逆に、最も効率悪く作っていった場合、何回目までグループを作ったところで破綻する
か。すなわち、n+1 回目にどの3人を選んでも一度一緒にグループに入った2人が含まれてし
まう状態にできるnの最小値は?
DD++さんからのコメントです。(平成30年3月12日付け)
誰にも解いてもらえていないので...、数字だけ答えを言うと、19回です。それを実現する
方法がなかなか面白いので、興味がある方はぜひ考えてみてください。
GAIさんからのコメントです。(平成30年3月13日付け)
1: 1 2 3
2: 1 4 7
3: 1 5 8
4: 1 6 9
5: 1 10 13
6: 1 11 14
7: 1 12 15
8: 2 4 8
9: 2 5 9
10: 2 6 10
11: 2 7 11
12: 2 12 13
13: 3 4 15
14: 3 9 12
15: 3 12 14
16: 4 5 6
17: 7 8 9
18: 10 11 12
19: 13 14 15
ただし未完成です。こんな感じで作っていますがホントに19回の編成で破綻が生じるので
すか?
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月13日付け)
1,2,3
4,5,6
7,8,9
1,4,7
2,5,8
3,6,9
2,9,4
7,5,3
6,1,8
2,7,6
9,5,1
4,3,8
9,10,12
10,11,13
11,12,14
12,13,15
13,14,9
14,15,10
15,9,11
というのを思い付きました。題意を満たしていますでしょうか?
GAIさんからのコメントです。(平成30年3月14日付け)
凄い!これではありませんか。1〜9グループと9〜15グループに分けてみるとは思ってもい
ませんでした。しかも、9は両方のグループに含まれる。どんな思考経路でこれに辿り着いた
のですか?お見事としか言いようがありません。他にも例を作れないものなのだろうか?
DD++さんからのコメントです。(平成30年3月14日付け)
正解です。最も効率が悪いことを目指すと、最も効率よくグループを作る手段が必要になる
という、なんとも皮肉なオチなのでした。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月14日付け)
どんな思考経路でこれに辿り着いたのですか?
実は "Transylvania lottery" についての記憶がウッスラとありました。Transylvania lottery
では 1 から 14 までの自然数から、重複しない3つの数を乱択したものが当たり番号となる
もので、当選番号抽選の事前に購入する籤に、購入者が好きな3つの数を書き入れておき、
これが当選番号の3つの数と、2つ以上一致していれば、賞金がもらえる…という仕掛けの
ようです。
さて、事前にできるだけ少ない枚数の籤をそろえて、必ず少なくとも1枚は当たり籤になる
ようにしたい、それには何枚の籤が必要か、また、どんな数を書き込めばよいのか…という
テーマが考えられてきたということです。
さて、14の数を、1から7までと8から14までとのグループに分けます。ここでは前者をA
グループ、後者をBグループと呼んでおきます。抽選された当選番号の3つ組の自然数が2
つのグループに分布していますから、鳩ノ巣原理により、どちらか一方のグループには少な
くとも2つの当選番号が含まれています。
この2つ組の当選番号を必ず掬い取るために、Fano平面を使えばよい、というのが面白い
ポイントなのでした。
今回の御出題では14ならぬ15になっています。そこでひと工夫が必要なのですが、最初
私はひとつのファノ平面ともうひとつのアフィン平面を使うことを思い立ちました。前者では7
個の数、後者では9個の数をカバーしますので、計16個の数をカバーすることとなります。
《これは失敗だ》と思い、あれこれ考えあぐねていたところ、AグループとBグループとで、同
一の数を使える(ただしひとつだけ)と気がついた次第です。
他にも例を作れないものなのだろうか?
なにかあれば面白そうですね。
また、《19が最小》という証明が私には思い付きません。
GAIさんからのコメントです。(平成30年3月16日付け)
DD++さんに見習って、16人から4人を選んでグループを作ることを繰り返す。ただし、一度
でも一緒にグループに入った人は、二度と一緒にグループに入らないようにするものとする。
最も効率悪く作っていった場合、何回目までグループを作ったところで破綻するか。すなわ
ち、n+1 回目にどの4人を選んでも一度一緒にグループに入った2人が含まれてしまう状態
にできるnの最小値は?またその組み合わせは?
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月14日付け)
nの最小値が不明のままですけれども、現時点で私の手元にある最良のものを投稿いたします。
n=14 まではOKで、n=15 で破綻するものです。
1 4 7 10
2 5 8 10
3 6 9 10
1 6 8 11
2 4 9 11
3 5 7 11
1 5 9 12
2 6 7 12
3 4 8 12
1 2 3 13
4 5 6 13
7 8 9 13
10 11 12 13
13 14 15 16
GAIさんからのコメントです。(平成30年3月17日付け)
私が見つけていたのは、20個だったので遥かに少ないです。フォーチュンさんはこれらの
組み合わせをみつけられるのがうまいですね。
昨日まる一日、朝6時から始めて、夜11時にようやく探し当てたテーマがあるので、良かっ
たら挑戦して下さい。(もっと効率よい組み方があれば知りたいので・・・)
[問題] 25人のクラスでバスケットボール(5人チーム)のチームを5班作り一日かけて試合
した。次の日も昨日とは違う組み合わせの班をやはり5つ作り対戦した。
これを6日間続けたら、どの生徒も他の人たち同じチームとして戦ったことになっていたという。
さて、この全部で30チームの班編成はどの様になされたのか?
DD++さんからのコメントです。(平成30年3月17日付け)
私も14日解は数分で見つけましたが、無駄がかなり多いので、もっと少なくいけそうな気が
しています。3人グループより4人グループの方が問題として遥かに難しいんですよね……。
ところで、上記の問題、5班で試合すると1つ班が余りそうですが、そこはどうするんでしょう?
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月17日付け)
きっとクラス対抗だったのですね。
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25 |
|
1 7 13 19 25
2 8 14 20 21
3 9 15 16 22
4 10 11 17 23
5 6 12 18 24 |
|
1 8 15 17 24
2 9 11 18 25
3 10 12 19 21
4 6 13 20 22
5 7 14 16 23 |
|
1 9 12 20 23
2 10 13 16 24
3 6 14 17 25
4 7 15 18 21
5 8 11 19 22 |
|
1 10 14 18 22
2 6 15 19 23
3 7 11 20 24
4 8 12 16 25
5 9 13 17 21 |
|
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25 |
※上記は《効率よく》組んだものですよね。下記は効率が悪く組んでみたものです。タイトル
通りに「最悪の手段」となっているのかどうかについては不安です。
1 2 7 12 17
3 6 14 15 17
4 5 8 11 17
9 10 13 16 17 |
|
1 3 8 13 18
2 4 15 16 18
5 6 7 9 18
10 11 12 14 18 |
|
1 4 9 14 19
2 6 8 10 19
3 5 12 16 19
7 11 13 15 19 |
|
1 5 10 15 20
2 3 9 11 20
4 6 12 13 20
7 8 14 16 20 |
|
1 6 11 16 21
3 4 7 10 21
8 9 12 15 21
2 5 13 14 21 |
|
17 18 19 20 21
21 22 23 24 25 |
n=22 までOKで、n=23 で破綻しています。
GAIさんからのコメントです。(平成30年3月18日付け)
自分が丸一日をかけやっとできた
A2 A5 C3 C4 B1 | B2 B5 D3 D4 C1 | C2 C5 E3 E4 D1 | D2 D5 A3 A4 E1 | E2 E5 B3 B4 A1
A3 A1 C4 C5 B2 | B3 B1 D4 D5 C2 | C3 C1 E4 E5 D2 | D3 D1 A4 A5 E2 | E3 E1 B4 B5 A2
A4 A2 C5 C1 B3 | B4 B2 D5 D1 C3 | C4 C2 E5 E1 D3 | D4 D2 A5 A1 E3 | E4 E2 B5 B1 A3
A5 A3 C1 C2 B4 | B5 B3 D1 D2 C4 | C5 C3 E1 E2 D4 | D5 D3 A1 A2 E4 | E5 E3 B1 B2 A4
A1 A4 C2 C3 B5 | B1 B4 D2 D3 C5 | C1 C4 E2 E3 D5 | D1 D4 A2 A3 E5 | E1 E4 B2 B3 A5
A1 B1 C1 D1 E1 | A2 B2 C2 D2 E2 | A3 B3 C3 D3 E3 | A4 B4 C4 D4 E4 | A5 B5 C5 D5 E5
に較べ、スッキリとしていますね。(幾何的構造を利用できるんだ!)
とても参考になりました。ありがとうございます。
DD++さんからのコメントです。(平成30年3月18日付け)
あ、対戦相手のことは考えない感じなんですかね。だとすると、「拡張カークマン問題」に
GAIさん自身が既に答えを書いているような。
もっとも、円は5つ用意した方が図が1つで済んでわかりやすいと思いますけどね。
5つの同心円上に5人ずつ等間隔に並べます。
初日は中心から見て同じ方向にいる人でチームを作ります。
2日目は、内側の円から順に、動かない、1/5周移動、2/5周移動、3/5周移動、4/5周移動
(いずれも時計回り)に移動し、中心から見て同じ方向にいる人でチームを作ります。
3日目、4日目、5日目も同様に繰り返します。
6日目は同じ円周上の人でチームを作ります。(おしまい)
GAIさんからのコメントです。(平成30年3月18日付け)
いろいろなパターンをあれこれ挑戦していたので、一度発見していたやり方をすっかり忘
れていました。
ところで、このバスケット組み合わせの問題を、クラスの人数を増やして45(人)とし、毎日
9班のチーム編成を11日間したとき、どの人も他の44(人)と同じチームになったとする場合
の99個の班編成をやろうとしているのですが(組合せ理論(ホール著)の本を読みながら挑
戦中)、そこに書いてある内容とそれらしき解として、
元(x,y,z) mod(3,3,5)
[(0,1,0),(0,2,0),(1,0,2),(2,0,2),(0,0,1)]mod(3,3,5)
[(2,1,0),(1,2,0),(2,2,2),(1,1,2),(0,0,1)]mod(3,3,5)
[(0,0,0),(0,0,1),(0,0,2),(0,0,3),(0,0,4)]mod(3,3,-)
と表してあることの意味が全く判読できずに途方に暮れています。これは前のように幾何的
構造の利用は可能なんでしょうか?
DD++さんからのコメントです。(平成30年3月18日付け)
多分これ、毎日9班を11日の解ではなく、毎日1班を99日やる解ですね。おそらくその読み
方は、例えば、
元(x,y,z) mod(3,3,5)・・・45人に (x,y,z) という値の組で名前をつけなさい。ただし、x と y は
mod3 で、z は mod5 とします。
[(0,1,0),(0,2,0),(1,0,2),(2,0,2),(0,0,1)]mod(3,3,5)
・・・45人の中から適当にリーダーを決めて、そのリーダーは、x と y は mod3 で、z は mod5
で考えて、
・自分より y の値が1大きい人
・自分より y の値が2大きい人
・自分より x の値が1大きく、z の値が2大きい人
・自分より x の値が2大きく、z の値が2大きい人
・自分より z の値が1大きい人
の5人を選んで班を作りなさい。(リーダー自身は入らないんかい!)
リーダーが x の値 3通り、y の値 3通り、zの値 5通り、全45通りを網羅するまでやりなさい。
[(2,1,0),(1,2,0),(2,2,2),(1,1,2),(0,0,1)]mod(3,3,5)・・・同様なので略。
[(0,0,0),(0,0,1),(0,0,2),(0,0,3),(0,0,4)]mod(3,3,-)
・・・前半は同様なので略。リーダーが x の値 3通り、y の値 3通り、全9通りを網羅するまで
やりなさい。
幾何学的には不可能ではないと思いますが、これら3つの方向全てが周回するように取ら
なければいけないので、かなり高次元の幾何学になりますね。
GAIさんからのコメントです。(平成30年3月19日付け)
貴重なヒントを元に構成してみました。ただ見易いように45(人)は(x,y,z) mod(3,3,5)の代わ
りに数字1〜45で表しソートした形式で提示しました。
確かに各自11回競技に参加することになり、またどの人も他のメンバーと同じチームで戦
う経験をすることになりました。
これはカークマンの時の様に、一日あたり9チームずつ重複しない班編成は無理なんでしょ
うね。ちょっとそれを確認するエネルギーは残っていませんでした。
DD++さんからのコメントです。(平成30年3月19日付け)
この組み方じゃなく別の組み方ならいけるんじゃないかと思います。あるいはこの組み方
でも上手くやればできるのか。
今までカークマン一般化で解があったものを振り返ると、おそらく解が存在するのはグルー
プ人数 k が素数冪で、全人数が k(k-1) を法として k と合同なときじゃないかと予想されます。
5 は素数冪(というか素数そのもの)で、45≡5 (mod20) ですから、この問題も多分上手く
やれば可能なんじゃないかなあと。
DD++さんからのコメントです。(平成30年3月17日付け)
とりあえず、13日解見つけました。A1からA8、B1からB4、C1からC4と名付けて、
01日目 A1 A2 A4 C1
02日目 A2 A3 A5 C2
03日目 A3 A4 A6 C3
04日目 A4 A5 A7 C4
05日目 A5 A6 A8 C1
06日目 A6 A7 A1 C2
07日目 A7 A8 A2 C3
08日目 A8 A1 A3 C4
09日目 A1 A5 B1 B2
10日目 A2 A6 B2 B3
11日目 A3 A7 B3 B4
12日目 A4 A8 B4 B1
13日目 C1 C2 C3 C4
14日目 破綻
これでもまだ無駄が多く(具体的には01日目から08日目にCの人が入っている意味が何も
ない)、もっと短い解もあるんじゃないかと思います。
DD++さんからのコメントです。(平成30年3月18日付け)
12日解、できました。A1からA6、B1からB6、C1からC4と名付けて、
01日目 A1 A2 A3 C1
02日目 A3 A4 A5 C2
03日目 A5 A6 A1 C3
04日目 A2 A4 A6 C4
05日目 B1 B2 B3 C1
06日目 B3 B4 B5 C2
07日目 B5 B6 B1 C3
08日目 B2 B4 B6 C4
09日目 A1 A4 B1 B4
10日目 A2 A5 B2 B5
11日目 A3 A6 B3 B6
12日目 C1 C2 C3 C4
13日目 破綻
これでもまだ無駄が多いですね。効率の悪さの無駄が多いというのも変な表現ですが。
01日目から08日目にCの人が入っている意味が何もなく、09日目から11日目はA同士や
B同士の残りを埋めているだけなので、AとBを同じグループに入れている意味が全くない…。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月18日付け)
DD++さん、13日解、12日解、お見事です。既に乾いた布のように感じますがまだまだ絞れ
ますでしょうか……。
ハンニバル・フォーチュンさんからのコメントです。(平成30年3月19日付け)
12日解の別解をみつけました。
01日目 A1 B1 C1 D1
02日目 A2 B2 C2 D2
03日目 A3 B3 C3 D3
04日目 A4 B4 C4 D4
05日目 A1 A2 A3 A4
06日目 B1 B2 B3 B4
07日目 C1 C2 C3 C4
08日目 D1 D2 D3 D4
09日目 A1 B2 C3 D4
10日目 A2 B4 C1 D3
11日目 A3 B1 C4 D2
12日目 A4 B3 C2 D1
13日目 破綻
DD++さんからのコメントです。(平成30年3月19日付け)
新たなアプローチです。本題の前にまず、こんな問題を解いておきます。
目盛りのない定規に3つの印をつけて、指定の長さを全て測れるようにしなさい。指
定の長さは、(9-1)/2以下の自然数のうち4の倍数でないものとする
印の数の3、意味深な式の中の9、倍数として除外される4、がそれぞれ何を意味するかの
種明かしは後ほど。
指定の長さを具体的に書くと、1,2,3 なので、「最初の印から見て右に1のところと3のところ
に印をつける」が答えです。それを踏まえてこんなことをしてみます。
X を 9-1=8 個書き並べます。
XXXXXXXX
左端を A に変えます。さらに、先ほどの問題の答えである「右に1のところと3のところ」も
A に変えます。
AAXAXXXX
A を書いた場所の4つ右を全部 B に書き換えます。
AAXABBXB
先頭にXを書き足します。
XAAXABBXB
2文字目を削除して最後尾に回すというのを 4-1=3 回繰り返し、全部で4つの文字列にし
ます。
XAAXABBXB
XAXABBXBA
XXABBXBAA
XABBXBAAX
さて、この9文字ずつの文字列4つが何を意味するか。
m文字目とn文字目を比べると、どの2箇所を見ても、4つの文字列のうち1つだけで文字が
一致しています。つまりこれは、最近流行の例のやつの「全9人、3人組、4日間」の解(グル
ープ名付き)の表現になっています。
1人目は4日ともX班に参加、2人目は3日目だけX班で他の日はA班に参加、3人目は1日目
と3日目はA班、2日目はX班、4日目はB班に参加、以下略、ということですね。
最初に突然現れた、印の数の3、意味深な式の中の9、倍数として除外される4、がそれぞ
れ何に対応する数なのかはもうお分りでしょう。
「全16人、4人組、5日間」をやってみましょう。最初の定規の問題はこうです。
目盛りのない定規に4つの印をつけて、指定の長さを全て測れるようにしなさい。指
定の長さは、(16-1)/2以下の自然数のうち5の倍数でないものとする
具体的には、1,2,3,4,6,7 の長さが測れればよいので、「最初の印から見て右に 1,3,7 のと
ころに印をつける」が答えです。それを踏まえて作業です。
X を 16-1=15 個書き並べます。
XXXXXXXXXXXXXXX
左端を A に変えます。さらに、先ほどの問題の答えである「右に 1,3,7 のところ」も A に変
えます。
AAXAXXXAXXXXXXX
A を書いた場所の5つ右を全部 B に書き換えます。
AAXAXBBABXXXBXX
B を書いた場所の5つ右を全部 C に書き換えます。
この過程は同時に作るグループ-2回繰り返してください。
さらに、今回は右にはみ出るので、そのような場合は左にぐるっと戻って数えるものとしま
す。
AACAXBBABXCCBCX
先頭にXを書き足します。
XAACAXBBABXCCBCX
2文字目を削除して最後尾に回すというのを 5-1=4 回繰り返し、全部で5つの文字列にし
ます。
XAACAXBBABXCCBCX
XACAXBBABXCCBCXA
XCAXBBABXCCBCXAA
XAXBBABXCCBCXAAC
XXBBABXCCBCXAACA
「全16人、4人組、5日間」の解(グループ名付き)完成です。
本質としては円周上と中心に人を並べているのと似たようなものですが、別方向から見る
ことで新しい発想のタネにならないかと感じたのと、掲示板で記述しやすい(この場では重要
事項)ということから紹介してみます。
以下、興味を持ってくださった方用の問題。
(1) 「目盛りのない定規に5つの印をつけて、指定の長さを全て測れるようにしなさい。指定の
長さは、(25-1)/2以下の自然数のうち6の倍数でないものとする」を解いてください。
(2) 「全25人、5人組、6日間」の解を構成してください。
(3) 「全49人、7人組、8日間」の解はこの方法で構成できるでしょうか?
GAIさんからのコメントです。(平成30年3月19日付け)
(3)について、 まだこのパターンは発表されていないものだったので、自分ができそうなや
り方で挑戦してみました。(7次のアフィン平面での並行直線を利用する。)
チェックせずにアップしていますので、どこか間違っているかもしれません。
GAIさんからのコメントです。(平成30年3月20日付け)
次の組み合わせは、異なる31個から任意の10個ずつを適当に選び出すことを31回やった
とき、どの数も10回ずつ使用したことになり、しかも同じグループに属した他のメンバーとは
どの人とも3回ずつ顔を合わせることになっていることが起こる。
B1 : 1 2 11 13 17 21 22 24 25 31
B2 : 1 2 3 4 5 6 7 29 30 31
B3 : 1 2 4 8 9 11 15 16 18 28
B4 : 1 3 7 8 10 14 15 17 21 27
B5 : 1 3 11 14 19 20 22 26 28 29
B6 : 1 4 9 10 19 21 23 25 26 30
B7 : 1 5 6 8 12 13 15 19 20 25
B8 : 1 5 13 14 16 18 22 23 27 30
B9 : 1 6 9 12 17 18 24 26 27 29
B10 : 1 7 10 12 16 20 23 24 28 31
B11 : 2 3 5 9 10 12 16 17 19 22
B12 : 2 3 12 14 15 18 23 25 26 31
B13 : 2 4 8 12 20 21 22 23 27 29
B14 : 2 5 10 11 15 20 24 26 27 30
B15 : 2 6 7 9 13 14 16 20 21 26
B16 : 2 6 8 14 17 19 23 24 28 30
B17 : 2 7 10 13 18 19 25 27 28 29
B18 : 3 4 6 10 11 13 17 18 20 23
B19 : 3 4 8 13 16 19 24 26 27 31
B20 : 3 5 9 13 15 21 23 24 28 29
B21 : 3 6 11 12 16 21 25 27 28 30
B22 : 3 7 8 9 18 20 22 24 25 30
B23 : 4 5 7 11 12 14 18 19 21 24
B24 : 4 5 9 14 17 20 25 27 28 31
B25 : 4 6 10 14 15 16 22 24 25 29
B26 : 4 7 12 13 15 17 22 26 28 30
B27 : 5 6 8 10 18 21 22 26 28 31
B28 : 5 7 8 11 16 17 23 25 26 29
B29 : 6 7 9 11 15 19 22 23 27 31
B30 : 8 9 10 11 12 13 14 29 30 31
B31 : 15 16 17 18 19 20 21 29 30 31
一連の組み合わせを利用して整然と並べる問題を構成している中で、上記の配列が一定
の手順を組んでいくことで達成できることに感動しました。
なお、この組み方は、色々な分割的サイクリックを巧みに織り交ぜて、まるで複雑な模様を
編み上げている編み物をやっている気分でした。
単純に計算して、まず31から10個を組合す数が[31]C[10]=44352165(通り)あり、さらに、そ
の中から31種類(ブロック)を選ぶ方法で、
[44352165]C[31]
= 137826659531115769503835398625895684263268873718071242441652812883164204230
292011728991674786197280692483308756627233186490326433875260138698475631781
024328722466133177973048116811476787426394780091053680 (204桁の数字)
の莫大な中で、この組み合わせを構成させられる手段を編み出せる人間の知恵の凄さに
改めて感心します。
(追記) HN「ナカノ」さんからご投稿いただきました。(令和6年8月3日付け)
以前、このサイトをたまたま見つけ、いろんな記事を見てたら少しずつ数学の面白さを感じ
始め、今では本サイト以外にも他の数学サイトに入り浸り、投稿するまでになりました。中で
もカークマンの問題は面白く、ブロックデザインという高校では習わなかった分野はお気に入
りです。今回は自分なりにブロックデザインを作成する手順を見つけたので見てください。
(→ 「自分なりのカークマンシステム」)
kuiperbelt さんからのコメントです。(令和6年8月8日付け)
https://mathlog.info/articles/gZIAjg3NYuY3HzADwIYS
https://mathlog.info/articles/3652
を拝見しました。
N=4(=2^2)の場合は、GF(4)(=GF(2^2))上のアフィン平面について、上記にあった「カークマン
女学生麻雀大会」の16人の女学生の場合の(v,b,r,k,λ)=(16,20,5,4,1)のブロックデザインにお
いて記載されているように、
(0,0) (1,0) (a,0) (b,0)
(0,1) (1,1) (a,1) (b,1)
(0,a) (1,a) (a,a) (b,a)
(0,b) (1,b) (a,b) (b,b)
の16個の点を含みます。ここで、a^2+a+1=0、b=a+1 です。
N=4の場合の射影平面ですが、有限体GF(4)上の3次元の同次座標を(x,y,z)とすると、z≠0
の場合は、射影関係により有限体GF(4)上の2次元のアフィン座標(x/z,y/z)と対応して、16個
の点からなり、z=0 の場合は無限遠点で、(kx,ky,0)(k=1,a,b) を同一視すると、
(1,0,0),(0,1,0),(1,1,0),(1,a,0),(a,1,0)の5個の点からなるので、合計すると、21(=4^2+4+1)個の点
から成ります。
z≠0の場合は、(kx,ky,kz)(k=1,a,b)を同一視するので、(x,y,1)で代表して、以下のように1〜16
の番号をつけます。
1:(0,0,1) 2:(1,0,1) 3:(a,0,1) 4:(b,0,1)
5:(0,1,1) 6:(1,1,1) 7:(a,1,1) 8:(b,1,1)
9:(0,a,1) 10:(1,a,1) 11:(a,a,1) 12:(b,a,1)
13:(0,b,1) 14:(1,b,1) 15:(a,b,1) 16:(b,b,1)
そして、残りの5個の無限遠点については、1-2-3-4を結ぶ「直線」の延長上の無限遠点に
17という番号をつけ、以下、1-5-9-13,1-6-11-16,1-8-10-15,1-7-12-14を結ぶ「直線」の延
長上の無限遠点に順次18,19,20,21と番号をつけていきます。
1:(0,0,1)- 2:(1,0,1)- 3:(a,0,1)- 4:(b,0,1)-17:(1,0,0)
1:(0,0,1)- 5:(0,1,1)- 9:(0,a,1)-13:(0,b,1)-18:(0,1,0)
1:(0,0,1)- 6:(1,1,1)-11:(a,a,1)-16:(b,b,1)-19:(1,1,0)
1:(0,0,1)- 8:(b,1,1)-10:(1,a,1)-15:(a,b,1)-20:(1,a,0)
1:(0,0,1)- 7:(a,1,1)-12:(b,a,1)-14:(1,b,1)-21:(1,b,0)
この射影平面上の「直線」は以下の21本となります。
1-2-3-4-17,5-6-7-8-17,9-10-11-12-17,13-14-15-16-17,1-5-9-13-18,2-6-10-14-18,
3-7-11-15-18,4-8-12-16-18,1-6-11-16-19,2-5-12-15-19,3-9-8-14-19,4-7-10-13-19,
1-8-10-15-20,2-7-9-16-20,3-6-12-13-20,4-5-11-14-20,1-7-12-14-21,2-8-11-13-21,
3-5-10-16-21,4-6-9-15-21,17-18-19-20-21
21本の「直線」上にはいずれも5点が乗っており、「班編成」についての平成30年1月29日
付けでのGAIさんからのコメントで、「入居者n^2-n+1名の老人ホームではn人がグループで
毎日散歩へ出掛けるルールがある。但し、道案内のため昨日散歩へ参加したn人のうち必ず
1人は次の散歩グループの班長として次も参加するものとする。このことをn^2-n+1日間続け
たとき、どの人も計n回散歩に出掛けたことになると言い、またどの人も他のn^2-n人と一緒
に散歩したことがあると言った」のn=5の場合のグループの作り方に相当します。
GF(3)上の3次元射影空間のブロックデザインについては、「カークマン女学生麻雀大会」の
40人の女学生の場合の(v,b,r,k,λ)=(40,130,13,4,1)の場合に相当します。
有限体GF(3)上の4次元の同次座標を(x,y,z,w)とすると、w≠0の場合は、射影関係により
有限体GF(3)上の3次元のアフィン座標(x/w,y/w,z/w)と対応して、27個の点からなり、w=0の
場合は無限遠点で、(x,y,z,0)と(2x,2y,2z,0)を同一視して13個の点からなるので、合計すると
40(=3^3+3^2+3+1)個の点から成ります。
w≠0の場合は、(kx,ky,kz,kw)(k=1,2)を同一視するので、(x,y,z,1)で代表して、以下のように
1〜27の番号をつけます。
1:(0,0,0,1) 2:(1,0,0,1) 3:(2,0,0,1)
4:(0,1,0,1) 5:(1,1,0,1) 6:(2,1,0,1)
7:(0,2,0,1) 8:(1,2,0,1) 9:(2,2,0,1)
10:(0,0,1,1) 11:(1,0,1,1) 12:(2,0,1,1)
13:(0,1,1,1) 14:(1,1,1,1) 15:(2,1,1,1)
16:(0,2,1,1) 17:(1,2,1,1) 18:(2,2,1,1)
19:(0,0,2,1) 20:(1,0,2,1) 21:(2,0,2,1)
22:(0,1,2,1) 23:(1,1,2,1) 24:(2,1,2,1)
25:(0,2,2,1) 26:(1,2,2,1) 27:(2,2,2,1)
残りの13個の無限遠点について、以下のように28〜40の番号をつけます。1-10-19を結ぶ
直線の延長上の無限遠点に28という番号をつけ、以下、1-11-21,1-12-20,…の直線の延長
上の無限遠点に順次29,30,…と番号をつけていきます。
1:(0,0,0,1)-10:(0,0,1,1)-19:(0,0,2,1)-28:(0,0,1,0)
1:(0,0,0,1)-11:(1,0,1,1)-21:(2,0,2,1)-29:(1,0,1,0)
1:(0,0,0,1)-12:(2,0,1,1)-20:(1,0,2,1)-30:(2,0,1,0)
1:(0,0,0,1)-13:(0,1,1,1)-25:(0,2,2,1)-31:(0,1,1,0)
1:(0,0,0,1)-14:(1,1,1,1)-27:(2,2,2,1)-32:(1,1,1,0)
1:(0,0,0,1)-15:(2,1,1,1)-26:(1,2,2,1)-33:(2,1,1,0)
1:(0,0,0,1)-16:(0,2,1,1)-22:(0,1,2,1)-34:(0,2,1,0)
1:(0,0,0,1)-17:(1,2,1,1)-24:(2,1,2,1)-35:(1,2,1,0)
1:(0,0,0,1)-18:(2,2,1,1)-23:(1,1,2,1)-36:(2,2,1,0)
1:(0,0,0,1)- 2:(1,0,0,1)- 3:(2,0,0,1)-37:(1,0,0,0)
1:(0,0,0,1)- 4:(0,1,0,1)- 7:(0,2,0,1)-38:(0,1,0,0)
1:(0,0,0,1)- 5:(1,1,0,1)- 9:(2,2,0,1)-39:(1,1,0,0)
1:(0,0,0,1)- 6:(2,1,0,1)- 8:(1,2,0,1)-40:(2,1,0,0)
無限遠点28には、直線
1-10-19,2-11-20,3-12-21,4-13-22,5-14-23,6-15-24,7-16-25,8-17-26,9-18-27
の9本の直線が通り、同様に無限遠点29〜40についてもアフィン空間上の点から9本ずつ
の直線が通るので、まず、13×9=117本の直線が含まれます。それに加えて、無限遠点を
相互に結ぶ以下の13本の直線が追加されるので、合計130本の直線が含まれます。
37-38-39-40,28-29-30-37,28-31-34-38,28-32-36-39,31-32-33-37,29-32-35-38,34-35-36-37,
30-33-36-38,28-33-35-40,30-32-34-40,29-33-34-39,30-31-35-39,29-31-36-40
このようにしてつくった有限体GF(3)上の3次元射影空間は、40個の点と130本の直線を含
んでいて、(40,4,1)-デザインとなり、任意の異なる2個の点に対し、その2個の点を全て含む
ブロックの元はちょうど1個であるという条件も満たすので、2-(40,4,1)-デザインとなります。
130本の直線を10本の直線からなる13組の平行類へ分類するパターンから、40人の女子
学生の10卓への13日間の組み分けのパターンが得られるので、Magma Free Online Calculator
の力を借りて求めると、一例として、
1日目
{1,2,3,37},{10,14,18,39},{21,23,25,40},{4,13,22,28},{8,16,27,30},{9,12,24,31},{6,17,19,33},{5,11,26,34},{7,15,20,36},{29,32,35,38}
2日目
{16,17,18,37},{19,22,25,38},{1,6,8,40},{5,14,23,28},{3,10,20,29},{7,11,24,32},{2,13,27,33},{9,15,21,34},{4,12,26,36},{30,31,35,39}
3日目
{7,8,9,37},{20,23,26,38},{10,15,17,40},{2,12,19,29},{6,14,22,30},{1,13,25,31},{5,16,21,33},{3,18,24,34},{4,11,27,35},{28,32,36,39}
4日目
{19,20,21,37},{3,4,8,39},{12,14,16,40},{6,13,23,29},{7,18,26,30},{2,15,25,32},{9,11,22,33},{1,17,24,35},{5,10,27,36},{28,31,34,38}
5日目
{12,15,18,38},{19,23,27,39},{2,4,9,40},{8,17,26,28},{1,11,21,29},{5,13,24,30},{7,10,22,31},{6,16,20,32},{3,14,25,33},{34,35,36,37}
6日目
{1,10,19,28},{5,15,22,29},{9,17,25,30},{8,11,23,31},{3,13,26,32},{4,18,20,33},{6,12,27,34},{7,14,21,35},{2,16,24,36},{37,38,39,40}
7日目
{22,23,24,37},{11,14,17,38},{2,6,7,39},{9,16,26,29},{1,12,20,30},{3,15,27,31},{5,18,19,32},{4,10,25,34},{8,13,21,36},{28,33,35,40}
8日目
{10,11,12,37},{21,22,26,39},{3,5,7,40},{6,15,24,28},{8,18,25,29},{4,16,19,31},{1,14,27,32},{2,17,23,34},{9,13,20,35},{30,33,36,38}
9日目
{2,5,8,38},{20,24,25,39},{11,13,18,40},{3,12,21,28},{7,17,27,29},{4,15,23,30},{1,16,22,34},{6,10,26,35},{9,14,19,36},{31,32,33,37}
10日目
{25,26,27,37},{10,13,16,38},{1,5,9,39},{2,11,20,28},{4,14,24,29},{6,18,21,31},{7,12,23,33},{8,15,19,35},{3,17,22,36},{30,32,34,40}
11日目
{3,6,9,38},{11,15,16,39},{20,22,27,40},{2,14,26,31},{4,17,21,32},{8,10,24,33},{7,13,19,34},{5,12,25,35},{1,18,23,36},{28,29,30,37}
12日目
{4,5,6,37},{21,24,27,38},{12,13,17,39},{7,16,25,28},{3,11,19,30},{9,10,23,32},{1,15,26,33},{8,14,20,34},{2,18,22,35},{29,31,36,40}
13日目
{13,14,15,37},{1,4,7,38},{19,24,26,40},{9,18,27,28},{2,10,21,30},{5,17,20,31},{8,12,22,32},{3,16,23,35},{6,11,25,36},{29,33,34,39}
となります。
カークマンの話で出てきたアーサー・ケイリーですが、八元数のことをケイリー数ともいって、
これは、ジョン・グレイヴスとは独立に八元数を発見したアーサー・ケイリーに因んでいます。
八元数には7つの虚数単位がありますが、7つの虚数単位の相互の積を記憶する方法で、
ファノ平面((7,3,1)-デザイン)が用いられています。
以下、工事中!



