| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俀係 | 暯惉俀侾擭搙屻婜 | 墶昹崙棫戝妛 | 岺妛晹 | 丒丒丒 | 俀師娭悢乮悢妛嘥乯 | 丂傗傗擄 |
丂弇惗傛傝儂僢僩側擖帋栤戣偑擖庤偱偒偨偺偱丄偳偙偺梊旛峑傛傝傕愭偵夝摎傪岞奐偟偨偄
偲巚偆丅僀儊乕僕揑偵媮傔傞椞堟傪椶悇偡傞偙偲偼壜擻偩傠偆偑丄偦偺傛偆側夝摎偱偼崌奿
揰傪摼傞偙偲偼擄偟偄偩傠偆丅偒偭偪傝偲榑棟揑偵媮傔傜傟傞栤戣側偺偱丄寁嶼偱惓妋偵媮
傔偨偄丅
丂偙偺傛偆側僞僀僾偺擖帋栤戣偼昿弌栤戣偱丄偄偝偝偐捖晠偺姶偑偁傞偑丄庼嬈摍偱偼嫵偊
偒傟側偄晹暘偱傕偁傞偺偱丄奺屄恖偺宱尡偺桳柍偑戝偒偔塭嬁傪梌偊傞栤戣偲傕尵偊傛偆丅
丂側偍丄偙偺栤戣偼曪棈慄偺栤戣偲傕娭楢偟丄悢妛揑偵偼旕忢偵柺敀偄栤戣偱傕偁傞丅
丂摉HP偺師偺儁乕僕傪嶲峫偵偝傟傞偲棟夝偑恑傓偙偲偩傠偆丅
丂丂丂丂嬋慄孮偺捠夁斖埻丂丂丂丂丂曪棈慄
墶昹崙棫戝妛丂岺妛晹乮俀侽侽俋乯
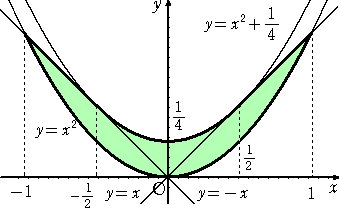
丂曻暔慄 倷亖倶2 忋偵俀揰俹乮 倲 丆 倲2 乯丄俻乮 倲亄侾 丆 乮倲亄侾乯2 乯傪偲傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂倲 偑偡傋偰偺幚悢傪摦偔偲偒丄捈慄俹俻偑捠夁偡傞椞堟傪媮傔傛丅
乮俀乯丂倲 偑 亅侾亝倲亝侽 偺斖埻傪摦偔偲偒丄慄暘俹俻偑捠夁偡傞椞堟傪媮傔丄恾帵偣傛丅
乮夝乯乮侾乯丂捈慄俹俻偺孹偒偼丄丂乷乮倲亄侾乯2亅倲2乸/乷乮倲亄侾乯亅倲乸亖俀倲亄侾丂側偺偱丄
丂丂丂丂丂捈慄俹俻偺曽掱幃偼丄丂倷亖乮俀倲亄侾乯乮倶亅倲乯亄倲2亖乮俀倲亄侾乯倶亅倲2亅倲
丂丂丂丂丂偄傑丄揰乮 倶 丆 倷 乯偑捈慄俹俻偺捠夁偡傞椞堟撪偺揰偲偡傞偲丄
丂丂丂丂丂丂倷亖乮俀倲亄侾乯倶亅倲2亅倲丂偲側傞幚悢 倲 偑懚嵼偡傞丅
丂丂丂丂丂偡側傢偪丄倲 偺俀師曽掱幃丂倲2亄乮侾亅俀倶乯倲亄倷亅倶亖侽丂偑幚悢夝傪帩偮丅
丂丂丂丂丂敾暿幃傪俢偲偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂俢亖乮侾亅俀倶乯2亅係乮倷亅倶乯亖侾亄係倶2亅係倷亞侽
丂丂丂丂丂丂傛偭偰丄丂倷亝倶2亄侾/係丂偑媮傔傞椞堟傪昞偡丅
乮俀乯丂慄暘俹俻偑捠夁偡傞椞堟撪偺揰傪乮 倶 丆 倷 乯偲偡傞偲丄丂亅侾亝倶亝侾丂偑惉傝棫偮丅
丂丂丂倷亖俥乮倲乯亖乮俀倲亄侾乯倶亅倲2亅倲亖亅倲2亄乮俀倶亅侾乯倲亄倶亖亅乷倲亅乮倶亅侾/俀乯乸2亄倶2亄侾/係
丂丂傛傝丄幉偺曽掱幃偼丄丂倲亖倶亅侾/俀丂偱偁傞丅傑偨丄忋幃偑慄暘俹俻傪昞偡偨傔偵偼丄
丂丂丂丂丂丂倲亝倶亝倲亄侾丂丂偡側傢偪丄丂丂倶亅侾亝倲亝倶
丂丂偱側偗傟偽側傜側偄丅偙傟傜偺偙偲偵拲堄偟偰丄応崌偵暘偗偰峫偊傞丅
丂丂乮僀乯丂倶亅侾/俀亝亅侾丂偡側傢偪丂亅侾亝倶亝亅侾/俀丂偺偲偒丄
丂丂丂丂丂丂丂倶亅侾亝倲亝倶丂偲丂亅侾亝倲亝侽丂偺岎傢傝偼丄丂亅侾亝倲亝倶
丂丂丂丂丂偙偺斖埻偱丄娭悢 倷亖俥乮倲乯 偺抣堟傪媮傔傟偽丄丂俥乮倶乯亝倷亝俥乮亅侾乯
丂丂丂丂丂偡側傢偪丄丂俥乮倶乯亖乮俀倶亄侾乯倶亅倶2亅倶亖倶2丂丄俥乮亅侾乯亖亅倶亅侾亄侾亖亅倶丂傛傝丄
丂丂丂丂丂丂丂倶2 亝 倷 亝 亅倶丂偲側傞丅
丂丂乮儘乯丂亅侾亝倶亅侾/俀亝亅侾/俀丂偡側傢偪丂亅侾/俀亝倶亝侽丂偺偲偒丄
丂丂丂丂丂丂丂倶亅侾亝倲亝倶丂偲丂亅侾亝倲亝侽丂偺岎傢傝偼丄丂亅侾亝倲亝倶
丂丂丂丂丂偙偺斖埻偱丄娭悢 倷亖俥乮倲乯 偺抣堟傪媮傔傟偽丄丂俥乮倶乯亝倷亝倶2亄侾/係
丂丂丂丂丂偡側傢偪丄丂倶2 亝 倷 亝 倶2亄侾/係丂偲側傞丅
丂丂乮僴乯丂亅侾/俀亝倶亅侾/俀亝侽丂偡側傢偪丂侽亝倶亝侾/俀丂偺偲偒丄
丂丂丂丂丂丂丂倶亅侾亝倲亝倶丂偲丂亅侾亝倲亝侽丂偺岎傢傝偼丄丂倶亅侾亝倲亝侽
丂丂丂丂丂偙偺斖埻偱丄娭悢 倷亖俥乮倲乯 偺抣堟傪媮傔傟偽丄丂俥乮倶亅侾乯亝倷亝倶2亄侾/係
丂丂丂丂丂偡側傢偪丄丂俥乮倶亅侾乯亖乮俀倶亅侾乯倶亅乮倶亅侾乯2亅乮倶亅侾乯亖倶2丂傛傝丄
丂丂丂丂丂丂丂倶2 亝 倷 亝 倶2亄侾/係丂偲側傞丅
丂丂乮僯乯丂倶亅侾/俀亞侽丂偡側傢偪丂侾/俀亝倶亝侾丂偺偲偒丄
丂丂丂丂丂丂丂倶亅侾亝倲亝倶丂偲丂亅侾亝倲亝侽丂偺岎傢傝偼丄丂倶亅侾亝倲亝侽
丂丂丂丂丂偙偺斖埻偱丄娭悢 倷亖俥乮倲乯 偺抣堟傪媮傔傟偽丄丂俥乮倶亅侾乯亝倷亝俥乮倶乯
丂丂丂丂丂偡側傢偪丄丂倶2 亝 倷 亝 倶丂偲側傞丅
丂丂偙傟傜傪恾帵偟偰丄壓恾傪摼傞丅
丂丂丂丂丂丂丂