
丂椺偊偽丄曽掱幃丂倷亖俀倶亄侾丂偼丄倷 愗曅偑 侾 偱孹偒 俀 偺捈慄傪昞偡丅嵗昗暯柺忋偱偼丄
偨偩1偮偺捈慄偑昤偐傟傞丅
丂偙傟偵懳偟偰丄曽掱幃丂倷亖俀倣倶亄倣丂偵偍偄偰丄掕悢 倣 偑丄侽亙倣亙俀丂偺斖埻偺抣
傪偲傞偲偒丄曽掱幃偼柍悢偺捈慄孮傪昞偡丅偙偺応崌偵丄偦偺捈慄孮偺捠傝摼傞斖埻傪媮
傔傞偙偲偼丄擖帋栤戣偺昿弌暘栰偱偁傞偲摨帪偵戝曄嫽枴偁傞栤戣偲偄偊傛偆丅
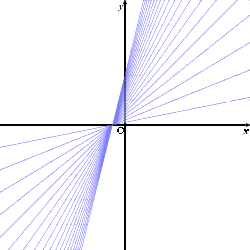
丂丂丂僌儔僼昤夋僜僼僩傪梡偄偰丄嵍恾偺傛偆側斖埻
丂丂偲側傞丅
丂丂丂捠忢丄寁嶼偱偼師偺傛偆偵偟偰帵偡偺偩傠偆丅
丂丂丂倷亖倣乮俀倶亄侾乯丂傛傝丄捈慄孮偼丄
丂丂丂丂丂掕揰 乮 亅侾/俀 丆 侽 乯
丂丂丂傪捠夁偡傞丅侽亙倣亙俀丂傛傝丄孹偒 俀倣 偼丄
丂丂丂侽亙俀倣亙係 側偺偱丄嵍恾傪摼傞丅
丂掕揰捠夁偺僥僋僯僢僋偼丄倣 偺 侾 師幃偺帪偼桳岠偩偑丄俀師埲忋偵側傞偲柍椡偩丅
椺丂曽掱幃丂倷亖俀倣倶亄倣2丂偵偍偄偰丄幚悢 倣 偺抣偑曄壔偡傞偲偒丄偦偺捈慄孮偼丄倷
丂丂幉傪幉偲偡傞丄偁傞曻暔慄偵忢偵愙偟偰偄傞偲偄偆丅偙偺曻暔慄偺曽掱幃傪媮傔傛丅
乮夝乯丂梌幃傪丄倣 偵娭偡傞俀師曽掱幃 丗 倣2亄俀倣倶亅倷亖侽丂偲峫偊偰丄幚悢夝傪帩偮忦
丂丂丂審傪挷傋傞丅敾暿幃傪 俢 偲偍偔偲丄丂俢/係亖倶2亄倷亞侽丂傛傝丄丂倷 亞亅倶2
丂丂丂丂偙偺偲偒丄媮傔傞俀師娭悢偼丄丂倷 亖亅倶2丂偱偁傞丅
丂丂丂幚嵺偵丄丂倷亖俀倣倶亄倣2丂偲楢棫偟偰丄丂倶2亄俀倣倶亄倣2亖侽
丂丂丂傛偭偰丄丂俢/係亖倣2亅倣2亖侽丂偐傜丄
丂丂丂丂丂丂丂捈慄孮偼忢偵曻暔慄丂倷 亖亅倶2丂偵愙偟偰偄傞丅丂乮廔乯
乮僐儊儞僩乯丂偙偺栤戣偱丄曻暔慄傪捈愙揑偵媮傔傞偙偲偼彮偟戝曄偩傠偆丅
丂丂丂丂丂丂嶲峫傑偱偵丄捈慄孮偺捠夁斖埻偼壓恾偲側傞丅
丂丂丂丂丂丂
丂倣 偺俀師幃偱丄倣 偑慡偰偺幚悢慡懱傪摦偔偲偒偼丄敾暿幃傪梡偄偰夝寛偝傟傞丅
丂偲偙傠偑丄擖帋栤戣偱偼 倣 偵惂尷傪晅偗偨傝庬乆偺婯惂偺傕偲偵夝偔偙偲傪梫媮偝傟傞丅
椺丂曽掱幃丂倷亖俀倣倶亄倣丂偵偍偄偰丄掕悢 倣 偑丄侽亙倣亙俀丂偺斖埻偺抣傪偲傞偲偒丄捈
丂丂慄孮偺捠傝摼傞斖埻傪暿側曽朄偱媮傔偰傒傛偆丅
丂丂倶 傪掕悢偲偟丄倣 偺娭悢 俥乮倣乯亖俀倣倶亄倣丂傪峫偊丄倷亖俥乮倣乯丂乮侽亙倣亙俀乯丂偐傜丄
丂倷 偺抣堟傪媮傔傛偆偲偡傞曽朄偱偁傞丅
丂丂偙偺曽朄偺桪傟偰偄傞揰偼丄倣 偺俀師幃偵尷傜偢丄擟堄偺応崌偵懳墳弌棃傞偲偙傠偱
丂偁傞丅
丂丂憗懍丄夝朄傪峫嶡偟偰偄偙偆丅
丂丂俥乮倣乯亖乮俀倶亄侾乯倣丂丂乮侽亙倣亙俀乯丂側偺偱丄
丂丂乮僀乯丂俀倶亄侾亜侽丂偺偲偒丄丂倷亖俥乮倣乯 偼扨挷憹壛偱丄丂俥乮侽乯亙倷亙俥乮俀乯
丂丂丂丂丂偡側傢偪丄丂倶亜亅侾/俀丂偺偲偒丄丂侽亙倷亙係倶亄俀
丂丂乮儘乯丂俀倶亄侾亖侽丂偺偲偒丄丂倷亖俥乮倣乯亖侽 偱丄 倶亖亅侾/俀丂偺偲偒丄丂倷亖侽
丂丂乮僴乯丂俀倶亄侾亙侽丂偺偲偒丄丂倷亖俥乮倣乯 偼扨挷尭彮偱丄丂俥乮俀乯亙倷亙俥乮侽乯
丂丂丂丂丂偡側傢偪丄丂倶亙亅侾/俀丂偺偲偒丄丂係倶亄俀亙倷亙侽
丂丂丂埲忋偐傜丄媮傔傞斖埻偼丄
丂丂丂丂丂丂丂
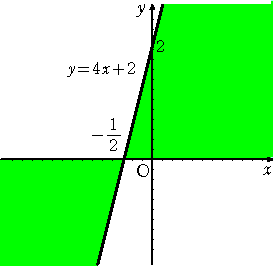
丂丂丂丂忋婰偺斖埻偵丄揰乮 亅侾/俀丂丆侽 乯偼娷傑傟傞偑丄嫬奅慄忋偺揰偼娷傑傟側偄丅
丂偙偺夝朄偺埿椡偼丄忋婰偺栤戣偱偼偁傑傝擣幆偝傟側偄偐傕偟傟側偄偑丄師偺栤戣偱偼丄
偦偺桳擄枴偑捝偄傎偳暘偐傞偱偁傠偆丅
椺丂曽掱幃丂倷亖俀倣倶亄倣2丂偵偍偄偰丄掕悢 倣 偑丄侽亙倣亙俀丂偺斖埻偺抣傪偲傞偲偒丄捈
丂丂慄孮偺捠傝摼傞斖埻傪媮傔偰傒傛偆丅
丂丂倶 傪掕悢偲偟丄倣 偺娭悢 俥乮倣乯亖俀倣倶亄倣2丂傪峫偊丄倷亖俥乮倣乯丂乮侽亙倣亙俀乯丂偐傜丄
丂傑偢丄倷 偺抣堟傪媮傔傞丅
丂丂俥乮倣乯亖倣2亄俀倣倶亖乮倣亄倶乯2亅倶2丂丂乮侽亙倣亙俀乯丂側偺偱丄
丂丂乮僀乯丂亅倶亝侽丂偡側傢偪丄倶亞侽 偺偲偒丄丂侽亙倣亙俀 偱 倷亖俥乮倣乯 偼扨挷憹壛側偺偱丄
丂丂丂丂丂丂俥乮侽乯亙倷亙俥乮俀乯丂偡側傢偪丄丂侽亙倷亙係倶亄係
丂丂乮儘乯丂侽亙亅倶亝侾丂偡側傢偪丄 亅侾亝倶亙侽 偺偲偒丄丂倣亖亅倶 偱嵟彫偱丄
丂丂丂丂丂丂俥乮亅倶乯亝倷亙俥乮俀乯丂偡側傢偪丄丂亅倶2亝倷亙係倶亄係
丂丂乮僴乯丂侾亙亅倶亙俀丂偡側傢偪丄 亅俀亙倶亙亅侾 偺偲偒丄丂倣亖亅倶 偱嵟彫偱丄
丂丂丂丂丂丂俥乮亅倶乯亙倷亙俥乮侽乯丂偡側傢偪丄丂亅倶2亝倷亙侽
丂丂乮僯乯丂亅倶亞俀丂偡側傢偪丄倶亝亅俀 偺偲偒丄丂侽亙倣亙俀 偱 倷亖俥乮倣乯 偼扨挷尭彮側偺偱丄
丂丂丂丂丂丂俥乮俀乯亙倷亙俥乮侽乯丂偡側傢偪丄丂係倶亄係亙倷亙侽
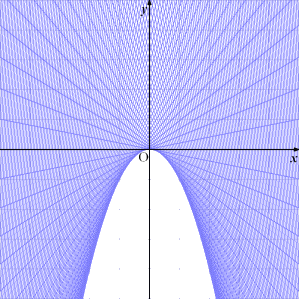
丂丂丂埲忋偐傜丄媮傔傞斖埻偼丄
丂丂丂丂丂丂丂

丂丂丂丂忋婰偺斖埻偵丄曻暔慄 倷亖亅倶2丂乮亅俀亙倶亙侽乯忋偺揰偼娷傑傟傞偑丄偦傟埲奜偺
丂丂丂嫬奅慄忋偺揰偼娷傑傟側偄丅
丂忋婰偱偼丄倷亖俀倣倶亄倣2丂傪 倣 偺娭悢偲偟偰丄偦偺抣堟偵拲栚偟偨偑丄倣 偺曽掱幃偲
尒偰丄偦偺夝偺懚嵼偵拲栚偡傞師偺傛偆側暿夝傕峫偊傜傟傞丅
丂偨偩丄忋婰偺夝朄傪抦偭偨屻偱偼斚嶨偵巚偊傞偙偲偩傠偆丅
乮暿夝乯丂俧乮倣乯亖倣2亄俀倣倶亅倷亖侽丂偑丄侽亙倣亙俀 偱彮側偔偲傕堦偮夝偑偁傞忦審傪媮傔
丂丂丂丂傟偽傛偄丅丂俧乮倣乯亖倣2亄俀倣倶亅倷亖乮倣亄倶乯2亅倷亅倶2丂傛傝丄幉偺幃偼丄倣亖亅倶
丂丂丂丂傛偭偰丄丂亅倶亝侽丂偡側傢偪丄倶亞侽 偺偲偒丄忦審傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂丂丂丂俧乮侽乯丒俧乮俀乯亙侽丂偡側傢偪丄丂亅倷丒乮係亄係倶亅倷乯亙侽
丂丂丂丂丂丂丂丂丂丂丂丂丂備偊偵丄丂倷丒乮倷亅係倶亅係乯亙侽
丂丂丂丂丂丂丂丂丂丂侽亙亅倶亝侾丂偡側傢偪丄 亅侾亝倶亙侽 偺偲偒丄忦審傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂丂丂丂敾暿幃 俢/係亖倶2亄倷亞侽丂偱丄俧乮俀乯亖係亄係倶亅倷亜侽
丂丂丂丂丂丂丂丂丂丂丂丂丂備偊偵丄丂亅倶2亝倷亙係倶亄係
丂丂丂丂丂丂丂丂丂丂侾亙亅倶亙俀丂偡側傢偪丄 亅俀亙倶亙亅侾 偺偲偒丄忦審傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂丂丂丂敾暿幃 俢/係亖倶2亄倷亞侽丂偱丄俧乮侽乯亖亅倷亜侽
丂丂丂丂丂丂丂丂丂丂丂丂丂備偊偵丄丂亅倶2亝倷亙侽
丂丂丂丂丂丂丂丂丂丂亅倶亞俀丂偡側傢偪丄倶亝亅俀 偺偲偒丄忦審傪枮偨偡偨傔偵偼丄
丂丂丂丂丂丂丂丂丂丂俧乮侽乯丒俧乮俀乯亙侽丂偡側傢偪丄丂亅倷丒乮係亄係倶亅倷乯亙侽
丂丂丂丂丂丂丂丂丂丂丂丂丂備偊偵丄丂倷丒乮倷亅係倶亅係乯亙侽
丂丂丂埲忋偐傜丄媮傔傞斖埻偼丄
丂丂丂丂丂丂丂

丂丂丂丂忋婰偺斖埻偵丄曻暔慄 倷亖亅倶2丂乮亅俀亙倶亙侽乯忋偺揰偼娷傑傟傞偑丄偦傟埲奜偺
丂丂丂嫬奅慄忋偺揰偼娷傑傟側偄丅
丂偝傜偵丄師偺傛偆側暿夝傕峫偊傜傟傞丅
丂偙傟偼丄朻摢偺椺偱帵偟偨乽捈慄孮丂倷亖俀倣倶亄倣2丂偼丄曻暔慄 倷亖亅倶2 偵忢偵愙
偟偰偄傞乿偲偄偆惈幙傪棙梡偡傞傕偺偱偁傞丅
乮暿夝乯丂捈慄丂倷亖俀倣倶亄倣2丂偲曻暔慄 倷亖亅倶2 偼丄愙揰俹乮亅倣丆亅倣2乯偱愙偡傞丅
丂丂丂丂侽亙倣亙俀 傛傝丄愙揰俹偼丄曻暔慄 倷亖亅倶2 忋傪丄亅俀亙倶亙侽丂偺斖埻偱摦偔丅
丂丂丂丂傛偭偰丄壓恾傪摼傞丅
丂丂丂丂丂丂丂

丂丂丂丂忋婰偺斖埻偵丄曻暔慄 倷亖亅倶2丂乮亅俀亙倶亙侽乯忋偺揰偼娷傑傟傞偑丄偦傟埲奜偺
丂丂丂嫬奅慄忋偺揰偼娷傑傟側偄丅
乮僐儊儞僩乯丂偙偺暿夝偼姶摦揑偵旤偟偄両丏丏丏偱偡偹丅偱傕丄偙傟傪摎埬偵彂偄偨傜丄懡暘
丂丂丂丂丂丂嵦揰幰偵傛偭偰揰傪偁偘傞傋偒偐偳偆偐堄尒偑傢偐傟偦偆側丏丏丏梊姶丅
丂偝傜偵丄倣 偺師悢傪偁偘偰傒傛偆丅
椺丂曽掱幃丂倷亖俀倣倶亄倣3丂偵偍偄偰丄掕悢 倣 偑丄侽亙倣亙俀丂偺斖埻偺抣傪偲傞偲偒丄捈
丂丂慄孮偺捠傝摼傞斖埻傪媮傔偰傒傛偆丅
丂丂丂傑偢偼丄僌儔僼昤夋僜僼僩傪梡偄偰尒摉傪偮偗傛偆丅
丂丂丂丂
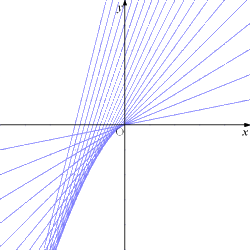
丂丂倶 傪掕悢偲偟丄倣 偺娭悢 俥乮倣乯亖俀倣倶亄倣3丂傪峫偊丄倷亖俥乮倣乯丂乮侽亙倣亙俀乯丂偐傜丄
丂傑偢丄倷 偺抣堟傪媮傔傞丅
丂丂俥乮倣乯亖倣3亄俀倣倶 傛傝丄丂俥乫乮倣乯亖俁倣2亄俀倶
丂丂乮僀乯丂倶亞侽 偺偲偒丄丂俥乫乮倣乯亞侽丂傛傝丄丂倷亖俥乮倣乯 偼扨挷憹壛側偺偱丄
丂丂丂丂丂丂俥乮侽乯亙倷亙俥乮俀乯丂偡側傢偪丄丂侽亙倷亙係倶亄俉
丂丂乮儘乯丂倶亙侽 偲偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
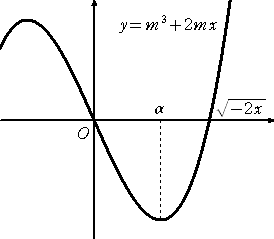
丂丂丂丂丂丂丂偵偍偄偰丄丂
丂丂丂丂丂丂傑偨丄
丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂偲偍偒丄丂兛亖俀丂偺偲偒偼丄丂倶亖亅俇
丂丂丂丂丂偦偙偱丄
丂丂丂丂丂丂乮鶣乯丂亅俀亝倶亙侽丂偺偲偒丄丂俥乮兛乯亝倷亙俥乮俀乯丂偡側傢偪丄亅俀兛3亝倷亙係倶亄俉
丂丂丂丂丂丂乮鶤乯丂亅俇亙倶亙亅俀丂偺偲偒丄丂俥乮兛乯亝倷亙侽丂偡側傢偪丄亅俀兛3亝倷亙侽
丂丂丂丂丂丂乮鶥乯丂倶亝亅俇 偺偲偒丄丂俥乮俀乯亙倷亙俥乮侽乯丂偡側傢偪丄丂係倶亄俉亙倷亙侽
丂丂丂丂丂偲側傞丅偙傟傪恾帵偡傟偽壓恾傪摼傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂

丂丂丂丂忋婰偺斖埻偵丄嬋慄 倷亖亅俀兛3丂乮亅俇亙倶亙侽乯忋偺揰偼娷傑傟傞偑丄偦傟埲奜偺
丂丂丂嫬奅慄忋偺揰偼娷傑傟側偄丅