| |
||||||
| 014 | 平成20年度前期 | 京都大学 | 理・甲 | ・・・ | 平面図形(数学A) | 易 |
角の二等分線の問題は大学入試では定番といっても過言ではないだろう。いろいろ形が
工夫されて楽しいくらいだ。(→ 参考:「角の二等分線の長さ」、「角の2等分」)
京都大学 理・甲(2008)・・・文との共通問題
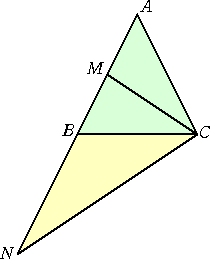 |
AB=AC である二等辺三角形ABCを考える。辺AB の中点をMとし、辺ABを延長した直線上に点Nを、 AN:NB=2:1 となるようにとる。 このとき、 ∠BCM=∠BCN となることを示せ。 |
(解1) ・・・ ACの中点を利用
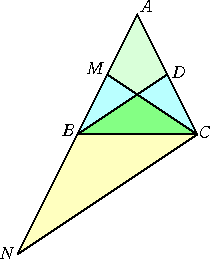 |
辺ACの中点をDとすると、明らかに、 △MBC≡△DCB よって、 ∠BCM=∠CBD また、△ANCにおいて、 B、Dは辺AN、ACの中点であるので、 中点連結の定理により、 BD よって、 ∠CBD=∠BCN 以上から、 ∠BCM=∠BCN (終) |
(コメント) △ANCにおいて、点Bが辺ANの中点なので、辺ACの中点を考えることは自然
ですね!
(解2) ・・・ 角の2等分線の性質を利用
 |
△ACMと△ANCにおいて、 ∠Aは共通 AC : AM=2 : 1=AN : AC なので、 △ACM ∽ △ANC よって、 AM : AC=MC : CN すなわち、AM=MB 、AC=AB=BN なので、 MB : BN=MC : CN |
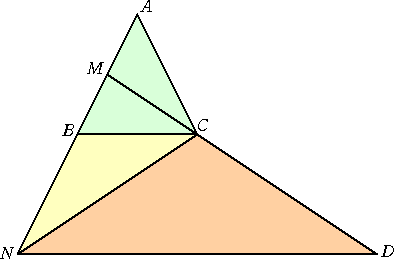
直線MC上に、 CN=CD となる点Dをとると、 MB : BN=MC : CD |
|
 |
|
よって、△MBC∽ △MND となり、 BC したがって、 ∠BCM=∠NDC=∠DNC=∠BCN (終) |
|
(コメント)上記証明で示したように、角の2等分線の性質は逆も成り立つのですね!
今まで使ったことがありませんでした...。
(解3) ・・・ 左右対称な図形の利用
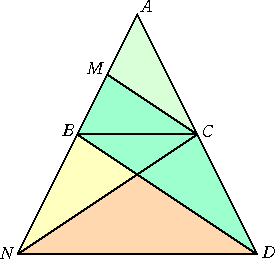 |
直線AC上に、 AC=CD となる点Dをとる。 このとき、 MC よって、 ∠BCM=∠CBD=∠BDN △BND≡△CND に注意して、 ∠BDN=∠CND=∠BCN 以上から、 ∠BCM=∠BCN (終) |
(コメント) 平面図形の醍醐味で、いろいろな別解が楽しめそうですね!
FNさんが、上記の問題について考察されました。(平成23年12月26日付け)
 |
初等幾何に慣れた人なら、(解1)や(解3)のように、 補助線を引いて簡明に解くだろう。 あまり初等幾何に慣れてない人は、私もそうだが、角 の2等分のイメージで、(解2)の方向の解になりそうな 気がする。角の2等分については、有名な性質 ∠BACの2等分線とBCとの交点をDとするとき、 BD : DC = BA : AC がある。 |
(解2)は、「これを利用」と書いてあるが、実際には使っていない。これのイメージで始めた
が、実際に必要なのは、これの逆なのでやめたということのようだ。
私なら使ってしまうだろう。
「MB : BN = MC : CN」がでた段階で、∠MCNの2等分線とMNの交点をDとして、
MD:DN=MC:CN と合わせて、B=Dを示すだろう。
(解1)の簡明さと比較すればあまり感心できない証明であるが...。
この問題を、座標やベクトルあるいは複素数で解くということはまず考えないだろうし、考
えるべきではないが、やってやれないことはないはずなので、座標を使って解いてみました。
内積の方が多少ましでしょうが、余弦定理にしました。
(解) Aを原点、ABを x 軸として、AB=2 とする。

上図において、A(0,0)、B(2,0)、M(1,0)、N(4,0) である。C(a,b)とおく。
a2+b2=4 だから、CM2=(a-1)2+b2=a2+b2-2a+1=5-2a
CB2=(a-2)2+b2=a2+b2-4a+4=8-4a 、CN2=(a-4)2+b2=a2+b2-8a+16=20-8a
このとき、
cos(∠BCM)=(CM2+CB2-MB2)/(2CM・CB)
=(5-2a+8-4a-1)/(2√(5-2a)√(8-4a))=(6-3a)/(2√(5-2a)√(2-a))
cos(∠BCN)=(CN2+CB2-BN2)/(2CN・CB)
=(20-8a+8-4a-4)/(2√(20-8a)√(8-4a))=(6-3a)/(2√(5-2a)√(2-a))
となって、 cos(∠BCM)=cos(∠BCN) より、 ∠BCM=∠BCN (終)
Aを原点にはするとして、ABを x 軸にしないで、AB=2 ともしないでやればもう少し面倒で
しょう。それを複素数を使ってやると次の問題に帰着します。
x、y は相異なる複素数で、|x|=|y|≠0 とするとき、(2x-y)(x/2-y)/(x-y)2
は実数であることを証明せよ。
複素数平面が高校数学から消えているので、いまどきはやらない問題ですが、やってみて
ください。
(コメント) B(x)、C(y) とすると、M(x/2)、N(2x) で、∠BCN=∠BCM すなわち、
arg((2x−y)/(x−y))=arg((x−y)/(x/2−y))
を示せばよいということですね。このことから、
arg((2x−y)(x/2−y)/(x−y)2)=0 即ち、(2x−y)(x/2−y)/(x−y)2 が実数を示
せばよいことになります。計算は大変そう〜な予感。
FNさんからのコメントです。(平成23年12月27日付け)
条件の「|x|=|y|≠0 」は、「|x|=|y|」でOKでした。計算は簡単とは言えません
が、それほどでもないです。
以下で、複素数 x の共役複素数を x~ で表すことにします。
|x|2=xx~ です。だから、条件|x|=|y|は、xx~=yy~ です。
z/w=zw~/ww~=zw~/|w|2 が実数 ⇔ zw~ が実数 が成り立ちます。
だから、 xx~=yy~ の条件のもとで、 (2x-y)(x/2-y)((x-y)2)~ が実数 であることを示せば
いいことになります。
凡人さんからのコメントです。(平成23年12月27日付け)
実際に、zw~ を計算しても、4次式の展開なので、確かにそれほど大変な計算でもないで
すね。
|x|=|y| を使って整理すると、 7|x|2-(9/2)(x~y+xy~)|x|2+(x~y)2+(xy~)2 となって、共役な複
素数の組 x~y、xy~ についての対称式になります。
FNさんからのコメントです。(平成23年12月27日付け)
2倍すれば、(2x-y)(x~-y~)(x-2y)(x~-y~) となって、前2つ、後2つの積を計算して、xx~=yy~
を使えば、2式は互いに共役となるから、その積は実数というような感じでもできます。
実際に、 (2x-y)(x~-y~)=2xx~-2xy~-x~y+yy~
(x-2y)(x~-y~)=xx~-xy~-2x~y+2yy~=2xx~-xy~-2x~y+yy~
より、{(2x-y)(x~-y~)}~=(x-2y)(x~-y~) なので、(2x-y)(x~-y~)(x-2y)(x~-y~) は実数。
冒頭の京都大学の問題は、次の問題の必要条件だけをきいている。
(A) ABの中点をM、ABを 2:1 に外分する点をNとするとき、点Pについて、AP=AB
が成り立つための必要十分条件は、∠BPM=∠BPNが成り立つことである。
軌跡の問題として書けば、
(B) ABの中点をM、ABを 2:1 に外分する点をNとする。∠BPM=∠BPN が成り立つ
点Pの軌跡を求めよ。
もとの問題は、この問題の逆のチェックの部分だけをきいている。問題の出し方としては、
(A)や(B)、特に、(B)の形が普通だと思う。
単なる想像だが、もともとは、(B)の形であったのではないか。出題者が逆のチェックがき
ちんとできるかどうかをみたいと言ったのに対し、それは期待できない、明文化しない限り
は、というような意見が出て、いっそ逆のチェックだけにしたらということで、この問題の形
になったのではないだろうか。軌跡の問題のおまけの逆のチェックとしては、そこそこの問
題だが、独立した問題とするにはちょっと軽すぎるかなという気がする。入試で出たとき解
ける自信があるわけでははないが...。
例 MがABの中点、NがABを 2:1 に外分する点となっています。これを一般化してください。
凡人さんからのコメントです。(平成23年12月27日付け)
少し見方を変えると、
「ANを s:1-s に内分する点をBとし、ABを s:1-s に内分する点をMとする。直線AB上にな
い点Cを、AB=ACとなるようにとるとき、∠BCM=∠BCNとなることを示せ。」
で、少し一般化できるかも。
FNさんからのコメントです。(平成23年12月27日付け)
多分同じでしょうが、m:nの形の表現で、(B)のタイプの問題として書けば、
(BB) ABを m:n に内分する点をM、ABを m+n:n に外分する点をNとする。
∠BPM=∠BPN が成り立つ点Pの軌跡を求めよ。
ところで、(B)についてですが、アポロニウスの円で容易と思って、それで終りにしていました。
アポロニウスの円って初等幾何でどうやって証明するんだったっけと思って考えたけど、よく
わからず、Wikiediaを見たら、内角と外角の2等分線の性質を使っていました。となると結構
難しいということになります。(B)はどうやって解くものでしょうか?
S(H)さんが、上記の問題について考察されました。(平成23年12月28日付け)
3点A、B、Cが単位円上に在り、A=(0,1) としても一般性を失うことはない。
C=( cos T ,sin T ) とすれば、 B=( -cos T ,sin T ) で、
vector CM を正規化し、vector CN を正規化し、加え、スカラー倍 t したものと
vector CB
が線型従属となれば、証明終了。
分かりやすく具現化すれば、紫枠の t が存在すれば証明終了。具現化した場合の t は黄
色枠の実数。∃t ∈ R 存在の耐えられない軽さ。紫枠の t∈R が存在すれば証明終了。存
在して草色枠。(→ 『存在の耐えられない重さの定理』例)
上記の問題を再考しました。
3点A、B、Cが単位円上に在り、A=(0,1) としても一般性を失うことはない。
C=( cos T ,sin T ) とすれば、 B=( -cos T ,sin T )、M=(
-cosT/2,1/2 + sinT/2))
このとき、ベクトルCN=CA+2AB=( -3cosT,−1 + sinT)
M に、超平面BC に関する対称変換S(H)を作用させると、
M’=(-cosT/2, -1/2 + 3sinT/2)
なので、ベクトルCM を超平面BCに関して対称変換すると、
CM’=(-3cosT/2, -1/2 + sinT/2 )
よって、 CN=2CM’が成り立ち、∠BCM=∠BCN である。
(ベクトル CM を超平面BC に関して対称変換するだけで解けてしまいました。)
(→ 参考:「鏡映」 英語版 ・ 独逸版)
(コメント) S(H)さんのエレガントな解答に感動しました。
S(H)さんからのコメントです。(平成23年12月30日付け)
上記の私の解答について、円函数を履修済の受験生を前提としていないが、こんな解答
があった。採点基準を見直しましょうとなることも想定され、減点されては堪らないので、円
函数を表に出さぬ解答を為してみました。
参考資料1 、参考資料2 、参考資料3 絡みなので、下はチラリと視て、この参考資料
達を深読みし、ご意見をお願い申しあげます。
参考資料3の青字を、以下の解答に使います。
3点A、B、C が単位円 U 上に在り、A=(0,1) としても一般性を失うことはない。
R∋t---F--->F(t)=((1 - t2)/(1 + t2),2t/(1 + t2))∈R2 とすると、像 F(R)=U ではなく、即
ち、F がUへの全射ではなく、以下ほんの一部欠陥が在るのですが、証明を進めます。
C={(1 - t2)/(1 + t2),2t/(1 + t2)}とすれば、 B= {-(1 - t2)/(1 + t2),2t/(1 + t2)}で、
M={-(1 - t2)/{2(1 + t2)},1/2 + t/(1 + t2)}
N=C+CA+2・AB={-2(1 - t2)/(1 + t2),-1 + 4t/(1 + t2)} となる。
M に超平面H:BC に関する対称変換S(H)を作用させ、ベクトルCMを超平面BCに関して
対称変換する。此れをスカラ-倍して、ベクトルCNになればよい。
CM’={-3(1 - t2)/{2(1 + t2)},-1/2 + t/(1 + t2)}
CN={-3(1 - t2)/(1 + t2),-1 + 2t/(1 + t2)}
よって、 CN=2CM’が成り立ち、∠BCM=∠BCN である。
ほんの一部、欠陥が在るので、減点パパにどうのこうの云われないよう注釈を加えて、証
明に欠陥が皆無の状況をつくって下さい。
(コメント) C={(1 - t2)/(1 + t2),2t/(1 + t2)}は、円 x2+y2=1 (ただし、(-1,0)を除く)の上
にある。題意から、-1<t<1 と仮定(即ち、Cの x 座標は正)しても一般性を失わない。
以下、工事中