０１０	平成１９年度前期	京都大学	文系	・・・	実数と論証	やや難

　計算は得意なのだが、この問題のような論証は弱いというのが昨今の高校生の現状だろ
う。分かり切ったことを如何に説得するか、その術が問われる。ただ、このような問題を普段
の授業等で扱うことは困難で、まさに受験生個々の数学のセンスが結果を左右する。


京都大学　文系（２００７）

　ｎ を １ 以上の整数とするとき、次の２つの命題はそれぞれ正しいか。正しいときは証明し、
正しくないときはその理由を述べよ。
　命題 ｐ ：　ある ｎ に対して、 と は共に有理数である。
　命題 ｑ ：　すべての ｎ に対して、− は無理数である。


　ｎ と ｎ＋１ は隣り合う整数で、十分大きい ｎ について両者はほぼ等しく共に有理数という
ことは期待できないし、小さい ｎ の値、たとえば、ｎ＝１、４、９、１６、・・・を代入して実験して
もやはり共に有理数にはなりえない。

　このことから、命題 ｐ は正しくないものと予想される。それに対して、命題 ｑ は直感的に正
しいものと予想される。

　このような事前考察を踏まえて、解答を考えてみよう。

（解）　命題 ｐ は正しくない。

　　　　（正しくない理由）　命題 ｐ が正しいとすると、ある ｎ に対して、 と 　は

　　　　　　　　　　　　　　　有理数となる。　ｎ は整数なので、 と は整数である。

　　　　　　　　　　　　　　　　このとき、　−＝１/（＋）　において、

　　　　　　　　　　　　　　　ｎ は、１ 以上の整数なので、　０＜−＜１

　　　　　　　　　　　　　　　これは、　 と 　が共に整数であることに矛盾する。

　　　　　　　　　　　　　　　　よって、命題 ｐ は正しくない。

　　　命題 ｑ は正しい。

　　　　（証明）　命題 ｑ が正しくないと仮定する。

　　　　　　　　　すなわち、ある ｎ に対して、− は有理数とする。

　　　　　　　　　このとき、　−＝ｍ　（ ｍ は有理数）　と書ける。

　　　　　　　　　　両辺の逆数を計算して、

　　　　　　　　　　　　　　　１/（−）＝１/ｍ

　　　　　　　　　すなわち、　　＋＝１/ｍ

　　　　　　　　　　よって、　＝（ｍ＋１/ｍ）/２　　、　＝−（ｍ−１/ｍ）/２

　　　　　　　　　ｍ は有理数なので、ある ｎ に対して、 と 　が共に有理数。

　　　　　　　　　しかるに、このことは決して起こりえない事柄である。

　　　　　　　　　　よって、命題 ｑ が正しくないと仮定したことにより、起こりえないことが起こ

　　　　　　　　　ったので、命題 ｑ は正しいものと判断される。　　（終）


　当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんが、上記の問題について考察された。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１２月１１日付け）

　正しくないときは「その理由を述べよ」となっていて、「証明せよ」とはなっていない。という
ことは、それほど厳格な書き方でなくてよいということだろう。だから、ここに書いてある解答
は多分満点をもらえると思う。

　大学の意図としては、証明も大事だが、その前に命題が正しいかどうかを判断する力を見
たいということだろう。証明は多少甘くなっても。

　命題ｐは正しくない。その理由を述べるのに、次のことを使っている。

　　ｎが1以上の整数で、が有理数なら、は整数である

　直感的には明らかである。だから、「その理由を述べよ」であるから、使ってもいいと思う。
この問題としてはかまわないだろう。

　ただ、これが証明不要なほど明らかかとなると疑問である。

　ｎ＝２ のとき、「が有理数なら、は整数である」となる。これが証明不要なら、「
は無理数」も証明不要となる。状況によっては証明不要だが、証明が必要なときもある。

　「は無理数である」

　「ｎが1以上の整数で、が有理数なら、は整数である」

　「代数的数で、かつ、有理数であれば、整数である」

　この順により一般的になるが、証明は似たようなものである。

　では、命題ｑを一般化した次の命題を証明してください。

　ｍ と ｎ は互いに素な自然数で、ｍ も ｎ も整数の平方ではないとする。ａ、ｂ、ｃ が
有理数で、ａ＋ｂ＋ｃ＝０ が成り立つなら、ａ＝ｂ＝ｃ＝０ である。


　ＦＮさんの問題を解いてみました。

（証明）　（ａ＋ｂ）²＝（−ｃ）²　より、　ａ²＋２ａｂ＋ｂ²ｍ＝ｃ²ｎ

　　　よって、　２ａｂ＝−ａ²−ｂ²ｍ＋ｃ²ｎ

　ここで、ａｂ≠０　とすると、が有理数となってしまうので、これは矛盾。

（補足：　＝ｑ/ｐ　（ｐ、ｑ は互いに素な整数で、ｐ≠０）とおくと、ｍ＝ｑ²/ｐ²
　　　　　ｍ は自然数なので、ｐ² すなわち、ｐ は１でなければならない。
　　　　　このとき、ｍ＝ｑ² となり、ｍ が整数の平方ではないことに矛盾する。）

　よって、　ａ＝０　または　ｂ＝０　である。

　ａ＝０　のとき、　 ｂ²ｍ＝ｃ²ｎ　において、ｂ≠０　とすると、　ｍ＝（ｃ/ｂ）²ｎ

　　ここで、ｂ、ｃ は有理数なので、ｃ/ｂ も有理数である。

　　そこで、　ｃ/ｂ＝ｑ/ｐ　（ｐ、ｑ は互いに素な整数で、ｐ≠０）とおくと、

　　　　ｍ＝（ｑ/ｐ）²ｎ　において、ｍ は自然数なので、ｎ は ｐ² で割り切れる。

　　　ｎ＝ｐ²・ｋ　（ｋ は自然数）　とおくと、　ｍ＝ｑ²・ｋ　と書ける。

　　　このとき、　ｍ と ｎ は、自然数 ｋ を公約数にもつ。

　　　ところが、ｍ と ｎ は、互いに素な自然数なので、ｋ＝１ でなければならない。

　　　すると、　ｍ＝ｑ²・ｋ＝ｑ²、ｎ＝ｐ²・ｋ＝ｐ²　となり、これは、ｍ も ｎ も整数の平方では

　　　ないことに矛盾する。よって、　ｂ＝０　であり、　ｃ＝０　から、ｃ＝０　でもある。

　ｂ＝０　のとき、　ａ＋ｃ＝０　において、ｃ≠０　とすると、　ｎ＝（ａ/ｃ）²

　　そこで、　ａ/ｃ＝ｑ/ｐ　（ｐ、ｑ は互いに素な整数で、ｐ≠０）とおくと、　ｎ＝（ｑ/ｐ）²

　　　　ｎ は自然数なので、ｐ＝１ でなければならない。すなわち、　ｎ＝ｑ²

　　　しかるにこれは、ｎ が整数の平方ではないことに矛盾する。

　　　よって、　ｃ＝０　で、ｂ＝０　より、　ｂ＝０　である。

　以上から、　ａ＝０　、ｂ＝０　、ｃ＝０　すなわち、　ａ＝ｂ＝ｃ＝０　　（証終）


　ＦＮさんからのコメントです。（平成２３年１２月１２日付け）

　私の問題に対する上記の解答は、おおむね正しいようです。ただ、３行目でが無理数
であることを証明なしで使っておられますが、これは証明した方がいいと思います。

　ｂ＝０ のときの証明は、事実上が無理数であることの証明ですから、が無理数で
あることを証明して、が無理数は「同様」ですませてしまっていいでしょう。

　これでいいでしょうが、ａ＝０ のときの証明もほとんど同じだということも気になると言えば、
なります。同じ様なルーチンが２つ以上あれば、１つのサブルーチンにまとめたいと感じます。

　そのように感じるなら、ｂ²ｍ＝ｃ²ｎ　から、ｍｎ＝（ｃｎ/ｂ）² として、√(ｍｎ)が無理数に持ち
込めば、すべて

　補題　が無理数

:の結果ということになります。もちろん、ｍｎが整数の平方でないことを確認する必要があり
ますが容易にできます。補題を、３回(ｍ、ｎ、ｍｎについて)使うことになります。

　もとの問題についてですが、今日、本屋に行って赤本を立ち読みしてきたら、

　「ｎ が1以上の整数で、が有理数なら、は整数である」

は証明してました。赤本としては当然でしょう。でも証明しなくても京大は○にするでしょう。

（別解）　（ｂ＋ｃ）²＝（−ａ）²　より、　２ｂｃ√（ｍｎ）＝ａ²−ｂ²ｍ−ｃ²ｎ

　　　　これと、もとの式より、

　　　　　ｂｃ≠０　のとき、√(ｍｎ)が有理数

　　　　　ｂ＝０、ｃ≠0　のとき、が有理数

　　　　　ｃ＝０、ｂ≠0　のとき、が有理数

　　「自然数 ｍ が整数の平方でないなら、は無理数」が証明できていれば、これらは
　
　すべて不可能となり、ｂ＝ｃ＝０　が出て、ａ＝０　もでる。　　（終）

　（注意）　もちろん、ｍｎが整数の平方でないことは示さないといけない。

　ａ＋ｂ＝−ｃ　として、両辺を２乗してもほぼ同じですが、ｂ²ｍ＝ｃ²ｎ　から、
ｍｎ＝（ｃｎ/ｂ）² とするような、やや不自然なことが必要なようです。


　立方根について、次のような問題はどうでしょうか。

　α＝とするとき、次が成り立つことを証明せよ。

　ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。

　いろんな証明があるようです。考えてみてください。

（コメント）　α の最小多項式が ｘ³−２　であることから明らかとするのが最短かな？


　ＦＮさんからのコメントです。（平成２３年１２月１３日付け）

　確かに前提とすることによっては明らかです。しかし、このページでは、高校数学あたりが
前提だと思われるし、前提は問題によって適切に決めるべきでしょう。

　最小多項式を定義するにはかなりの準備が必要です。また、ｘ³−２ が有理数係数で既約
であることの証明が必要です。後者は、が無理数であることとほぼ同じですが．．．。
この方向での証明を書きます。

　まず、αは無理数である。

　これも証明は必要ですが、が無理数であることとほとんど同じですから省略します。

　ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０ が成り立つとする。

　ａ≠0とする。ｘ³−２ を、ａｘ²＋ｂｘ＋ｃ で割ったときの商を、ｐｘ＋ｑ　余りを、ｒｘ＋ｓ とする。

　実際に割り算をすることを考えればわかるように、ｐ、ｑ、ｒ、ｓ は有理数である。

　　　ｘ³−２＝（ａｘ²＋ｂｘ＋ｃ）（ｐｘ＋ｑ）＋ｒｘ＋ｓ

　ｘ＝αを代入して、　ｒα＋ｓ＝０

　ここで、ｒ≠0　とすると、αが有理数になるから、ｒ＝０　従って、ｓ＝０

　このとき、　ｘ³−２＝（ａｘ²＋ｂｘ＋ｃ）（ｐｘ＋ｑ）

　ｐ≠０　で、ｘ＝−ｑ/ｐ は、ｘ³−２＝０　の解である。即ち、−ｑ/ｐ＝。

　が有理数となり矛盾である。　よって、ａ＝０

　ｂα＋ｃ＝０ において、ｂ≠０ とすると、αが有理数となり矛盾。

　　よって、ｂー０　で、ｃ＝０

（コメント）　簡明な証明をいただき、ＦＮさんに感謝します。高校生向けの解答を書く意識は
　　　　　　全くなく、数学をやっている人一般の感覚で、「α の最小多項式は、ｘ³−２　から
　　　　　　明らか」としてしまいました．．．ｆ(^^;)。


　らすかるさんからのコメントです。（平成２３年１２月１３日付け）

　α＝が有理数でないことを認めると、以下のようにも証明できますね。

（別証）　ａα²＋ｂα＋ｃ＝０ … (1) の両辺にαを掛けて、２ａ＋ｂα²＋ｃα＝０ … (2)

　　　(1)×ｂ−(2)×ａ　から、　 (ｂ²−ａｃ)α＋(ｂｃ−２ａ²)＝０

　　αは有理数でないことから、　ｂ²＝ａｃ　、ｂｃ＝２ａ²

　　よって、　ｂ³＝ａｂｃ＝２ａ³ なので、　ｂ＝２^1/3ａ

　　２^1/3 は無理数なので、　ａ＝ｂ＝０　で、(1)から、ｃ＝０　　（別証終）


　ＦＮさんからのコメントです。（平成２３年１２月１３日付け）

　証明としては、らすかるさんが書かれたのが普通だと思います。私の書いた解が別解の
感じです。

　「２つの方程式 ａｘ²＋ｂｘ＋ｃ＝０　、ｘ³−２＝０　が共通解をもつとき」という共通解の問題
なので、次数の高い式を次数の低い式で割って、というのもないことはないですが(私が書い
た解)、ｘ³＝２ を使って、次数を落としていくやり方(らすかるさんの解)の方が普通だと思い
ます。

　どちらの方法にしろ、まず、αが有理数でないこと、即ち、

　「ａ、ｂ が有理数で、ａα＋ｂ＝０　であれば、　ａ＝ｂ＝０」

を証明して、これを使って証明するという２段階の手順になります。

　これらと異なる面白い証明が書いてありました。これは２段階ではなく、一発で証明します。

　ｘ³＋ｙ³＋ｚ³−３ｘｙｚ＝(ｘ＋ｙ＋ｚ)(ｘ²＋ｙ²＋ｚ²−ｘｙ−ｙｚ−ｚｘ)　を使います。

　「ｘ＋ｙ＋ｚ＝０　のとき、　ｘ³＋ｙ³＋ｚ³−３ｘｙｚ＝０」を使って直接証明してください。
（αが有理数でないことは使わないで！）


　当ＨＰがいつもお世話になっているＨＮ「Ｓ（Ｈ）」さんが、

　α＝とするとき、次が成り立つことを証明せよ。

　ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。

という問題について考察された。（平成２３年１２月１６日付け）　（→　参考：「ｎ乗根」

　上記の問題は、人生が有限なので自明と想定の範囲外でなくパスして先に進みたいが、
考えてみてはと促され、少し考えてみました。

    ａｘ² + ｂｘ + ｃ = 0　且つ、 ｘ^m - 2 = 0　の問題提起(ｍ=3、4、5、6、・・・)

（ ｍ=4　なら本当は、ａｘ³ + ｂｘ² + ｃｘ + ｄ = 0　且つ、 ｘ^m - 2 = 0　と問題創作者かも？）

　ｍ=3 なら、　4ａ³ - 6ｂｃａ + 2ｂ³ + ｃ³=0  なる関係が在る。

　　自明でも導出過程を明記し、導出してください。

　　（実際に、連立方程式
　　　　　ａα²＋ｂα＋ｃ＝０　、ｂα²＋ｃα＋２ａ＝０　、ｃα²＋２ａα＋２ｂ＝０
　　が自明でない解（α²，α，１）をもつので、
　　　　　
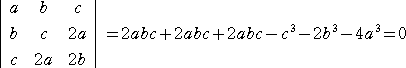
　　から、　4ａ³ - 6ｂｃａ + 2ｂ³ + ｃ³=0 　の成り立つことが分かる。

　　　あるいは、ａｘ² + ｂｘ + ｃ = 0　と ｘ³ - 2 = 0 が共通解を持つことから、終結式を計算し
　　てもいいだろう。終結式は、Ｓ（Ｈ）さんの好きな手法なので．．．。

　　　あるいは、（ａα²＋ｂα）³＝（−ｃ）³　を展開しても示される。）

　4ａ³ - 6ｂｃａ + 2ｂ³ + ｃ³=0  を解くと、

ｃ＝-ａα² - ｂα、(1 + ｉ・ａ)/α + (1 - ｉ・ｂ)/α²、(1 - ｉ・ａ)/α + (1 + ｉ・ｂ)/α²

　となり、　ａ=0　、ｂ=0 とならざるを得ない。(どちらかが０でなければ矛盾）

　従って、　ａ＝０　、ｂ＝０　、ｃ＝０

　m=4 なら、　4ａ⁴ - 4ｃ²ａ² + 8ｂ²ｃａ - 2ｂ⁴ + ｃ⁴=0　なる関係が在る。
（自明でも導出過程を明記し導出）

　これを解くと、

　　　　ｃ＝-ａ - ２^1/4ｂ、 ａ - ｉ・２^1/4ｂ、ａ + ｉ・２^1/4ｂ、-ａ + ｉ・２^1/4ｂ

　となり、　ａ=0　、ｂ=0 とならざるを得ない。(どちらかが０でなければ矛盾）

　従って、　ａ＝０　、ｂ＝０　、ｃ＝０

（コメント）　Ｓ（Ｈ）さん、証明をいただきありがとうございます。

　　　ｘ³ - 2 が有理数体上既約なので、αが ａｘ² + ｂｘ + ｃ = 0　を満たせば、ａ＝ｂ＝ｃ＝０

　とする解がやはり最善ですね！


　ＦＮさんが証明を与えられました。（平成２３年１２月１６日付け）

　ａα²＋ｂα＋ｃ＝０ を満たす有理数 ａ、ｂ、ｃ で、ａ＝ｂ＝ｃ＝０ ではないものがあるとする。

　ａ、ｂ、ｃ の分母の最小公倍数を両辺にかけて、ａ、ｂ、ｃ は整数としてよい。さらに、ａ、ｂ、ｃ

を、ａ、ｂ、ｃ の最大公約数で割って、ａ、ｂ、ｃ の最大公約数は１としてよい。即ち、

　　整数ａ、ｂ、ｃ の最大公約数が１で、ａα²＋ｂα＋ｃ＝０ が成り立つとする。

　「ｘ＋ｙ＋ｚ＝０　のとき、　ｘ³＋ｙ³＋ｚ³−３ｘｙｚ＝０」より、

　　（ａα²）³＋（ｂα）³＋（ｃ）³−３（ａα²）（ｂα）（ｃ）＝０

　すなわち、　ａ³α⁶＋ｂ³α³＋ｃ³−３ａｂｃα³＝０

　　α³＝２　を代入して、　４ａ³＋２ｂ³＋ｃ³−６ａｂｃ＝０

　従って、ｃ は偶数なので、ｃ＝２C とおくと、　４ａ³＋２ｂ³＋８Ｃ³−１２ａｂＣ＝０

　両辺を２で割って、　２ａ³＋ｂ³＋４Ｃ³−６ａｂＣ＝０　より、ｂ は偶数。ｂ＝２Ｂ とおくと、

　２ａ³＋８Ｂ³＋４Ｃ³−１２ａＢＣ＝０　で、両辺を２で割って、　ａ³＋４Ｂ³＋２Ｃ³−６ａＢＣ＝０

　従って、ａ は偶数となる。

　以上から、ａ、ｂ、ｃ がすべて偶数となり、ａ、ｂ、ｃ の最大公約数が１であることに反する。

　よって、ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。


　ちょっと面白い証明だと思います。
（→　参考：「大川研究室主催『数学の問題コーナー』に挑戦！ 問題４」）

　第１段階として、「ａ、ｂ が有理数で、ａα＋ｂ＝０　⇒　ａ＝ｂ＝０」を証明し、第２段階として、
「ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　⇒　ａ＝ｂ＝ｃ＝０」を証明するのと比べて、何か
利点があるかどうかはわかりません。S(H)さんが書かれていることはわかりません。コメント
として管理人さんが書かれていることはその通りです。特に、問題を一般化すれば。


　ＦＮさんからのコメントです。（平成２３年１２月２０日付け）

　この問題に関して、「大川研究室主催『数学の問題コーナー』に挑戦！ 問題４」が参考と
してあがっていたので、見てみました。全く同じ問題が載っていて、このやり方で解いてあり
ます。

　ｘ³−２ の既約性から容易に出るのに、そして、解き方についての指示もないのに、敢え
て、このやり方をするのはよくわかりません。しかも、αが無理数であることを使っています。
(使う必要はないけど）何故なのでしょう。わかりません。

　私が、このやり方を見たのは、数学セミナー1977年1月号(ちょうど35年前発行)のNOTE欄
です。もちろん、３５年前にみたのではなくて、１、２ヶ月前に見ました。

　1976年11月号のNOTE欄に出た読者の投稿(上記の問題の解答を、３通り書いたもの)に
対して「山本幸一教授から次のような御注意がありました」として書いてあったものです。

　最後に、「これが標準的な方法で、こうすれば、やが無理数であることの証明と同
じ手間でできる。」と書いてあります。やはりよくわかりません。


　ＦＮさんからのコメントです。（平成２３年１２月１６日付け）

　問題を少し一般化します。２の立方根を ｎ の立方根に変えます。もちろん、ｎ は整数の立
方ではないとします。

(1A) ｎ は自然数で整数の立方ではないとする。αを ｎ の立方根(実数)とするとき、

　「ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。」

　が成り立つことを証明せよ。

　これが次の主張とごく近いことは容易にわかります。

(1B) ｎ は自然数で整数の立方ではないとする。このとき、多項式 X³-ｎ は有理数係数の
　　範囲で既約であることを証明せよ。

(1C) ｎ は自然数で整数の立方ではないとする。αを ｎ の立方根(実数)とするとき、αは
　　無理数であることを証明せよ。

　ｎ=2 のときは、(1C)の証明は易しいので省略し、(1C)⇒(1A)の証明に主眼をおきました。

　ｎ になると、(1C)⇒(1A)の証明が、ｎ=2 のときと同じなのに対し、(1C)の証明はやや面倒
になります。だから(1C)⇒(1A)の証明はもういいとします。(1B)または(1C)を証明してくださ
い。

　多分、(1C)の方が簡単です。もちろん、(1B)を(1C)に帰着させるなら同じですが、(1B)を証
明するときは、Eisensteinの定理を使ってください。


　ＦＮさんが、(1C)の証明を与えられました。（平成２３年１２月２０日付け）

（証明）　ｎ の素因数 ｐ で、ｎ＝ｐ^ｋ・Ｎ　(ｐとNは互いに素)と表したとき、ｋが３の倍数でない

　ものが存在する。(そうでなければ、ｎ は立方数である)

　ｋ＝３ｍ＋ｒ　(ｒ＝１ または ２)で、立方根 ｎ＝ｐ^ｍ・立方根(ｐ^ｒ・N)　だから、立方根(ｐ^ｒ・N)

が無理数であることを示せばよい。

　これが有理数 ｓ/ｔ　(ｓ，ｔ は互いに素な整数)であるとする。

　　　ｓ³/ｔ³＝ｐ^ｒ・N　より、ｓ³＝ｐ^ｒ・N・ｔ³

　右辺は、ｐ の倍数だから、左辺も ｐ の倍数。　従って、ｓ は ｐ の倍数となる。ｓ＝ｐＳ　と

おく。これを代入して、　ｐ³・Ｓ³＝ｐ^ｒ・N・ｔ³ (ｒ＝１　または　２)だから、両辺を ｐ^ｒ で割ると、

　左辺は、ｐ の倍数だから、右辺の N・ｔ³ が ｐ の倍数となる。Nは、ｐ と互いに素だから、

ｔ が、ｐ の倍数となる。これは、ｓ、ｔ が互いに素であることに反する。

　よって、立方根 ｎ は無理数である。　　（証終）

（コメント）　ＦＮさんに感謝します。


　　　ＦＮさんからの追記です。（平成２３年１２月２０日付け）

　　　(1C)を対偶的な表現に書きなおせば、次のようになります。

　　　　「自然数 ｎ について、ｎ^1/3 が有理数であれば、ｎ は自然数の３乗である。」

　　　「不等式の評価」におけるらすかるさんの証明では、これよりはるかに強い次の命題
　　が使われています。

　　　　ａ が正の有理数 ｎ、ｍ が互いに素な自然数で、ａ^ｎ/ｍ が有理数であれば、
　　　ａ は有理数のｍ乗である

　　　証明に重点を置くなら、上の命題でも証明が必要と感じるし、普通に問題を解くときは、
　　下の命題でも証明が必要ないと感じます。「が無理数」でも、証明が必要なときもあ
　　るし、「自然数 ｎ について、√ｎ が有理数なら、√ｎ は整数」とかは普通は使っていい
　　のと同じでしょう。


　さらに一般化して、立方根を ｐ 乗根にかえると、(2A)は書くのが面倒で、(2B)と同じです。
(2C)は(2B)より弱い主張になります。

(2B) ｐ は素数、ｎ は自然数で、ｎ は整数の ｐ 乗ではないとする。このとき、多項式 X^p-ｎ
　　は有理数係数の範囲で既約であることを証明せよ。

　これは私は全くできてません。多分成り立つだろうと思います。間違っているかもしれませ
んが．．．。Eisensteinの定理だけでできる？


　Ｓ（Ｈ）さんからの続報です。（平成２３年１２月１６日付け）

　α＝とするとき、次が成り立つことを証明せよ。

　ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。

という問題について、飯高先生にも思い切ってお願いしたところ、即答していただきました！

　それは、現在９９％完成した「やさしい体論」に詳しくかいてあります。こっそりｔｅｘで知らせ
ます。（2011年12月16日(金)11時24分28秒　欣喜雀躍です！）

\section{無理数と１次独立性}
\subsection*{有理数体上１次独立}
\hspace*{1zw} 一般に複素数 $\alpha_1,\alpha_2, \cdots, \alpha_r$ が\textbf{有理数体上１次独立}とは,
\hspace*{1zw} 有理数 $k_1,k_2, \cdots, k_r$ が$$k_1\alpha_1 + k_2\alpha_2+ \cdots+ k_r\alpha_r=0$$
を満たすなら $k_1=k_2=\cdots=  k_r=0$ となることをいう.
\hspace*{1zw} 「$\sqrt[3]{5} $ は無理数である」は, 「1 と $\sqrt[3]{5} $ が有理数体上１次独立である」
といいかえることができる.
\hspace*{1zw}簡単のため $\beta=\sqrt[3]{5}$ とおく. このとき,
$1,\beta$ が有理数体上１次独立である. のみならず
$1,\beta, \beta^2$ も\textbf{有理数体上１次独立\index{ゆうりすうたい@有理数体上１次独立}になる}.
このことを証明しよう．
\subsection*{素朴な証明}
\hspace*{1zw}はじめに素朴な立場にたって証明する.
\hspace*{1zw}有理数 $k_1,k_2, k_3$ があって,
\begin{equation} \label{beta1}k_1+k_2\beta+ k_3\beta ^2=0
\end{equation}を満たすとする．このとき,$k_1=k_2= k_3=0$ を示せばよい．
$\bullet$
$k_3=0$ とすると$k_1+k_2\beta=0$ になり, 1 と $\beta $ は有理数体上１次独立であったから
$k_1=k_2=0$ をえる.
$\bullet$
$k_3 \neq0$ とする. 式 (\ref{beta1})を $-k_3$ で割ってから, $- \displaystyle\frac{k_1}{k_3}$ と
$- \displaystyle\frac{k_2}{k_3}$を あらためて$ k_1$ と $k_2$ とおくと式 (\ref{beta1}) は
\begin{equation}\label{beta2}k_1+k_2\beta=\beta^2
\end{equation}   になる.
$\beta ^3=5$ に注意し式 (\ref{beta2}) に $\beta $ を掛けると
\[k_1\beta+k_2\beta^2-5=0\]
\hspace*{1zw} 式 (\ref{beta2}) より $\beta ^2$ を $k_1+k_2\beta$ に置き換え次式をえる.
\[k_1\beta+k_2(k_1+k_2\beta)-5=0.\]これより
$$k_2k_1-5+(k_1+k_2^2)\beta=0. $$
\hspace*{1zw} 1 と $\beta $ は有理数体上１次独立なので
\[k_2k_1=5, k_1+k_2^2=0.\]
\hspace*{1zw} これより$5=(-k_2)^3$.  すなわち $\sqrt[3]{5}=-k_2$ をえるので, $\sqrt[3]{5}$
が有理数となって矛盾する.
\subsection*{多項式による別証明}
\hspace*{1zw} 式 (1.4) が成り立っているとして証明しよう.
$f(X)=X^3-5$ とおくと $f(\beta )=\beta ^3-5=0$ を満たす.
\hspace*{1zw} $g(X)= -k_1-k_2X + X ^2$ とおくとこれは有理係数の多項式で
$g(\beta)=0$ を満たす.そこで
$f(X)$ を $g(X)$ で割る. この 商を $q(X)$, 余りを $r(X)$と書けば
$q(X)$  と $r(X)$ は有理係数の多項式であり
\[f(X)=g(X)q(X)+r(X)\]を満たす．
$r(X)$ の次数は $g(X)$ の次数2より小さいから1以下になる.
\hspace*{1zw} $r(X)= f(X)-g(X)q(X)$ により$r(\beta)= f(\beta)-g(\beta)q(\beta)=0$をえる.
$r(X) \neq 0$ とすると $r(X)$ は有理係数の1次式 なので有理数 $c_0,c_1$ によって
$r(X)=c_0+c_1X$ とかけ, $r(\beta)=c_0+c_1 \beta=0$ を満たす.
\hspace*{1zw}これは 1 と $\beta$ の有理数体上１次独立性に反する.
\hspace*{1zw}したがって,$r(X) =0 $ になり,$f(X)=g(X)q(X)$ となる.
$q(X)$ は1次式になるので $q(X)=X-c (c \in \mathbb{Q})$ と書ける.
$f(c)=g(c)q(c)=0$ により $c^3=5$ となるので $\sqrt[3]{5}$ の無理数性に矛盾する.
\proofbox

--- 以上、飯高先生の上梓が近い書籍を購入すれば分かる悦びが得られそうです。

　α＝とするとき、次が成り立つことを証明せよ。

　ａ、ｂ、ｃ が有理数で、ａα²＋ｂα＋ｃ＝０　が成り立つなら、ａ＝ｂ＝ｃ＝０　である。

という問題について、誰にもこのような命題は量産可能です。例えば、

命題１ α=1/√（２ + ） とするとき、次が成り立つことを証明せよ。

　Q[α]∋ａ₃α³ + ａ₂α² + ａ₁α + ａ₀ = 0 が　成り立つなら、　ａ_ｊ = 0　(ｊ∈{0，1，2，3})

　このとき、ａ_ｊ の間に関係が在るのは自明としないで、

8ａ₀⁴ + 32ａ₂ａ₀³ - 16ａ₁²ａ₀² + 40ａ₂²ａ₀2 - 40ａ₃²ａ₀² - 48ａ₁ａ₃ａ₀²
　　　　　　+ 16ａ₂³ａ₀ - 24ａ₂ａ₃²ａ₀ - 16ａ₁²ａ₂ａ₀ - 32ａ₁ａ₂ａ₃ａ₀ + 4ａ₁⁴ + 2ａ₂⁴
　　　　　　　　　+ ａ₃⁴ + 8ａ₁ａ₃³ - 8ａ₁²ａ₂² + 20ａ₁²ａ₃² - 4ａ₂²ａ₃² + 16ａ₁³ａ₃ - 8ａ₁ａ₂²ａ₃=0

なる関係を導出しなさい、の方が愉しい問です。

命題２　α=1/√[7 + √（5 + ）]　とするとき、次が成り立つことを証明せよ。

　Q[α]∋ａ₇α⁷ + ａ₆α⁶ + ａ₅α⁵ + ａ₄α⁴ + ａ₃α³ + ａ₂α² + ａ₁α + ａ₀=0 が成り立つなら、
ａ_ｊ = 0　(ｊ∈{0，1，2，・・・，7})

　少し改竄し、

　Q（）[α]∋ａ₇α⁷ + ａ₆α⁶ + ａ₅α⁵ + ａ₄α⁴ + ａ₃α³ + ａ₂α² + ａ₁α + ａ₀=0 が成り立
つなら、ａ_ｊ = 0　(ｊ∈{0，1，2，・・・，7})

が成立するなら証明し、そうでないなら 0 でない ａ_ｊ ∈　Q()の例を記せ。

　更に改竄し、QにQ上代数的数達を添加し、拡大体　Q(____，_____，____，......，___) を構成し、
上の命題が破綻するようにして下さい。

　このとき、 ａ_ｊ の間に成り立つ関係式を導出願います。

　命題は量産できます。大學院生指導教授むけの命題のうちの一つについて、大學院生
指導教授が教授らしく解く発想を忖度し、その発想で高校生向けの命題をスパッと解いて
下さい。

　「商環」絡みで、「このような命題は誰にも量産可能です」を具現します。

α＝1 - 2^1/3 + 2^2/3 + 7^1/5 とするとき、次が成り立つことを証明せよ。

下の ａ_ｊ は全て有理数とする。全て ａ_ｊ=0 である。

(1)　ａ₁α+ａ₀ = 0
(2)　ａ₂α² + ａ₁α + ａ₀ = 0
(3)　ａ₃α³ + ａ₂α² + ａ₁α + ａ₀ = 0
(4)　ａ₄α⁴ + ａ₃α³ + ａ₂α² + ａ₁α + ａ₀ = 0
　・・・・・・・・・
　こんなケースでは、数学的帰納法が常套手段だとお考えでしょうが、今回は破綻するので
止して下さい。

(10)　ａ₁₀α¹⁰ + ａ₉α⁹ + ａ₈α⁸ + ａ₇α⁷ + ａ₆α⁶
　　　　　　　　　　　　　　　　　　　　　　　　+ ａ₅α⁵ + ａ₄α⁴ + ａ₃α³ + ａ₂α² + ａ₁α + ａ₀ = 0

　そろそろ上の命題は破綻しましすか？破綻するまで続行願います。容易ですが、破綻する
例を具現して下さい。

　α=1/√[7 + √（5 + ）]　の分母の有理化を多様な発想で解き、書籍=体論を読破すれ
ば、瞬時に解けることを本当に試して下さい。書籍=体論には、高校生や大學生が困難を極
める諸問題がスパッと解決する切れ味抜群の定理達が掲載される筈です。

　こう記述したので、此処を訪問される方は世界に数多存在する故、書籍=体論購入者が世
界に数多います。(日本語が讀めなくても心配ご無用。数式で理解しあえますから)