
「99101 と 10199 の大小を比べよ。」などという問題は昔からある有名問題である。
(→ 参考:「微積分の小技」)
問題を公式化すれば、
e<x<y である2つの正の数 x 、y に対して、x1/x>y1/y が成り立つ。
とでもなろうか...。(ただし、e は、Napier の数(自然対数の底)である。)
これは、関数 y=(log x)/x が、x>e において単調に減少することから明らかである。
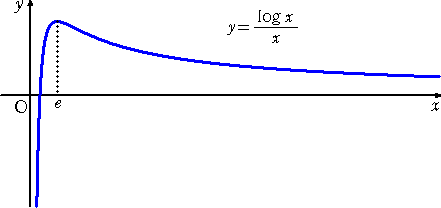
FNさんからのコメントです。(平成23年12月19日付け)
この曲線に関連して、 xy=yx を満たす x、y を求めることを考えます。
(1) 自然数 x、y (x<y)で、xy=yx を満たすものすべてを求めよ。
(2) 正の有理数 x、y (x<y)で、xy=yx を満たすものすべてを求めよ。
(1)はあまり難しくないです。(2)は難しいです。すべてと書いてるからといって有限個とは
限りません。
(コメント) (1)を考えてみた。
0<x<e なので、 x=1、2 の場合を考えればよい。
x=1 のとき、 1y=y1 を満たす y (1<y)は存在しない。
x=2 のとき、 2y=y2 より、2<y を満たす y は、y=4 のみである。
(2)について、らすかるさんが考察されました。(平成23年12月19日付け)
y=(1+1/t)x とおくと、 x(1+1/t)x={(1+1/t)x}x より、xx・xx/t=xx・(1+1/t)x
すなわち、 xx/t=(1+1/t)x より、 x1/t=1+1/t なので、 x=(1+1/t)t
t は有理数なので、 t=n/m (m、nは互いに素)とおくと、
x=(1+m/n)n/m={(m+n)/n}n/m
m+n と n は互いに素なので、x が有理数となるためには、
m+n=rm 、n=sm (r、s は自然数)
よって、 m=rm−sm=(r−s)Σ[k=0〜m-1](rk・sm-1-k)
r>s>0 なので、r>1 で、よって、m>1とすると、(右辺)>m となり矛盾するので、m=1
従って、 x=(1+1/n)n 、y=(1+1/n)n+1
具体的に値を求めると、n=1、2、3、・・・ について、
(x,y)=(2,4)、(9/4,27/8)、(64/27,256/81)、(625/256,3125/1024)、 …
と無数にある。
FNさんからのコメントです。(平成23年12月20日付け)
らすかるさんの解答は、鮮やかですね。私はかなり前にこの問題に出会ってちょっと考え
たけど、わからず答えを見ても長くてめんどくさそうで、また考えようとそのままにしていまし
た。 y=(1+1/t)x とおくのがキーのようですね。 y=(1+t)x でもいいけど、y=tx では駄目で、
y=(1+○)x の形で書くことが重要なようです。後はなんとかなりそうです。
FNさんからのコメントです。(平成23年12月21日付け)
(1)について、管理人さんが書かれているように、この(不等式の評価の)ページに書いて
あることを使って証明するのが一番簡単だと思います。このページに書いてあることを既知
としない形で証明を書きます。
(証明) xy=yx より、y・log x=x・log y なので、 (log x)/x=(log y)/y
ここで、f(x)=(log x)/x (x>0) とおく。
このとき、 f’(x)=(1−log x)/x2 より、f(x)は、0<x<e で単調増加、e<x で単調減少
このことから、x<y で xy=yx 即ち、f(x)=f(y) となるためには、0<x<e<y でなければ
ならない。従って、x=1 または 2 である。
x=1 のとき、1=y 、x<y だから、解なし。
x=2 のとき、 2y=y2 なので、y=2m (mは自然数)とおける。
22m=(2m)2=22m より、 2m=2m
m≧3 のとき、 2m>2m (きちんと証明するには数学的帰納法が必要?)
なので、 m=1、2
m=1 のとき、 y=2 よって、 (x,y)=(2,2)
これは、x<y に反する。
m=2 のとき、 y=4 よって、 (x,y)=(2,4) で、これは条件に適する。
さて、(1)は純然と整数の問題です。だから、指数・対数関数や微分を使わないで証明で
きないかと考えるのは自然です。らすかるさんの解を整数に限定すれば、解析的ではない
証明になりますが、分数指数も使わないことにします。整数だけの世界で、(1)を解くことは
できないでしょうか。素因数分解の一意性ぐらいで解けないかと思うのですが...。
らすかるさんからのコメントです。(平成23年12月21日付け)
素因数分解とか使わないので、期待されている解き方ではないと思いますが、とりあえず
整数だけでの解答です。
x=1 のとき、解がないから、x≧2
xy=yx の両辺を xx で割ると、 xy-x=(y/x)x だから、y は x で割り切れる。
y=tx (t≧2)とおくと、 xtx=(tx)x より、 xt=tx なので、 xt-1=t
t=3 のとき、 (左辺)≧4 から、 xt-1>t であり、
xt-1>t が成り立てば、 xt>xt-1・x>tx>t+1 なので、数学的帰納法により
t≧3 ならば、 xt-1>t
よって、 xt-1=t が成り立つならば、t=2 で、xt-1=t から x=2、y=tx=4
FNさんからのコメントです。(平成23年12月21日付け)
素因数分解ぐらいは必要かと思ったのですが、全然不要ですね。「yはxで割り切れる」が
出て、あとはほとんど不等式だけの感じです。一般には、左辺が右辺より相当大きくて勝負
にならないということでしょうか。多分最善の解でしょう。(2)も多分そうだから、(1)(2)は完
全解決のようです。
さて、本題に入ろう。上記の公式を知っていれば、「89と98で、どっちが大きい?」と問わ
れても、即座に自信を持って、「89>98 で、89 の方が大きい」と答えられる。
実際に、 81/8>91/9 から、89>98 は明らかだろう。
もっとも、上記の関数の存在を知らなくても、
89=227=(210)2・27>(103)2・128>106・102=108>98
と示せばよい。
ところで、Excel さんに手伝ってもらい、89=134217728 、98=43046721 である。
すなわち、 89÷98=134217728÷43046721=3.11795474503157・・・・・ である。
このことから、一見それほど違わないと思われる2つの数 89と98 は、実は、89 の方が
98 よりも3倍以上大きいことが分かる。
そこで、問題である。
89>3・98 であることを手計算で示すことは可能だろうか?
上記の不等式より評価が甘い次の不等式
89>2・98
を手計算で示すことは容易である。
(証明) 89=227=2・226 において、 28=256>243=35 から、 224>315
よって、 226=4・224>4・315>316=98 より、 89>2・98 (証終)
89>3・98
は、読者のための練習問題としよう。
FNさんからのコメントです。(平成23年12月19日付け)
89>3・98 であることを手計算で示すことは可能だろうか?
について、可能です。真面目に計算するのが一番早い。
左辺は、227で、右辺は、317
210=1024、27=128 だから、1024×1024×128 を計算する。
34=81 だから、 38=81×81=6561 なので、6561×6561×3 を計算する。
5分もあればできます。しかし、これでは面白くない。
(1+1/n)n は自然数 n の増加関数で、その極限が e であることは既知とする。
89>3・98 の両辺を、89 で割って、3をかけて、
3>(9/8)9 即ち、 (1+1/8)9<3
(1+1/8)9=(1+1/8)8・9/8 において、(1+1/8)8<e としたのでは評価が甘く証明
できない。 (1+1/8)8<(1+1/10)10 とすればできる。
(1+1/10)10=1+10C1(1/10)+10C2(1/10)2+・・・ において、初項は1、第2項も1、
第3項は0.45、第3項は0.12、第4項は0.021、第5項は0.00252、第6項以下は
0.00*** だから、 (1+1/10)10<2.6
よって、 (1+1/8)9=(1+1/8)8・9/8<(1+1/10)10・9/8<2.6×(9/8)<3
(とても5分や10分ではできません!)
227>317 は、対数で書けば、 27log102>17log103 です。
log102やlog103を評価する不等式で比較的容易に出て精度もいいのは、1024>1000
からでる log102>0.3 や、これと、81>80 からでる
log103>(3log102+1)/4>1.9/4=0.475
です。逆向きの不等式で精度のいいのはなさそうです。
9<10 からでる log103<0.5 が役に立つことはあまり期待できません。
27log102>17log103 を示す最善の方法は、多分直接計算で、227>317 を示すことで
しょう。つまらない結論ですが普通はそんなものでしょう。大学入試とかで普通に計算するよ
り良い方法があったりするのは、そのように問題が作ってあるからです。
(コメント) この問題は、一松 信 先生から伺ったもので、何か上手い手がありそうな雰囲
気です。
89>3・98 の証明を考えてみた。
89=227 で、 98=316 より、 3・98=317
ここで、 210=1024 より、 5・210=5120
また、 36=729 より、 7・36=5103 なので、 5・210>7・36
すなわち、 10・29>7・36 の両辺を3乗して、 1000・227>343・318=1029・317
このとき、 227>1.029・317>317 より、 89>3・98
(コメント) 上記のように証明らしく書いてはみたものの、FNさんの直接計算と五十歩百歩
だな〜というのが正直な感想!一松先生を唸らせるようなもっとエレガントな解答
はないのだろうか?
FNさんが、89>3・98 の証明を考えられました。(平成23年12月21日付け)
89>3・98 が証明しにくいということは、2つの値が近いということです。2の累乗と3の累
乗で値が近いものを調べてみました。2の50乗以下としました。比の値が1に近いという基
準でさがしてみました。
比の値が一番1に近いのは、312と219で、312/219=1.013・・・
2番目は、この問題の 227と317で、227/317=1.039・・・
312と219の方が、より近い値ですが、直接計算ですぐできてしまいます。ということで、227
と317あたりが問題として妥当ということでしょう。
もっと小さいところで、比の値が比較的1に近いのを調べてみました。
28=256と35=243 なら手計算で見つけられます。28/35=1.053・・・
上の2つほどではないけど、そこそこ1に近いです。
28>35 より、 8>5log23 なので、 log23<8/5
証明すべきことは、227>317 即ち、 27>17log23 から、 log23<27/17
もちろん、これの方がいい式だから、log23<8/5 から出ることはありません。
しかし、ヒントにはなります。256>243 は情報量を落とし過ぎです。256>243+12
ぐらいのぎりぎりにする必要があるでしょう。
28=256>243+12=35+12 の両辺を3乗して
224>(35+12)3>315+3・310・12=315+4・312
両辺に、23=8 をかけて、
227>8・315+32・312>8・315+315>317
よって、 227>317 すなわち、 89>3・98
これで、証明はできました。(1+1/10)10 を計算したのよりはましでしょう。単純計算よりい
いとは言えませんが。
らすかるさんからのコメントです。(平成23年12月22日付け)
単純計算より早い方法を考えてみました。
29=512 、35=243 から、 29>2.1・35
両辺を3乗して、 227>9.261・315>317
(コメント) なるほど〜。「29>2.1・35」とする方法が斬新で、気がつきませんでした。
FNさんからのコメントです。(平成23年12月22日付け)
227を作るのだから、28より 29の方がいいですね。
28/35>1.05 だから、29/35>2.1
だから、 2.13>9 を示せば終わりということですね。
空舟さんが、2a と 3b が近くなる時について考察されました。(平成24年2月12日付け)
上記のFNさんの考察:
89>3・98 が証明しにくいということは、2つの値が近いということです。2の累乗と3の累
乗で値が近いものを調べてみました。2の50乗以下としました。比の値が1に近いという基
準でさがしてみました。
比の値が一番1に近いのは、312と219で、312/219=1.013・・・
2番目は、この問題の 227と317で、227/317=1.039・・・
もっと小さいところで、比の値が比較的1に近いのを調べてみました。
28=256と35=243 なら手計算で見つけられます。28/35=1.053・・・
上の2つほどではないけど、そこそこ1に近いです。
無理数の分数近似といえば連分数近似です。
log102/log103=0.63092...=[0; 1,1,1,2,2,3,...]
これを使えば、2a = 3b となる b/a を、次のように得られる。
1/1+1/1+1/1 = 2/3 = 0.666...
1/1+1/1+1/1+1 = 3/5 = 0.6
1/1+1/1+1/1+1/2 = 5/8 = 0.625
1/1+1/1+1/1+1/2+1 = 7/11 = 0.6363...
1/1+1/1+1/1+1/2+1/2 = 12/19 = 0.6415...
1/1+1/1+1/1+1/2+1/2+1 = 17/27 = 0.6296...
1/1+1/1+1/1+1/2+1/2+1/3 = 41/65 = 0.6307...
1/1+1/1+1/1+1/2+1/2+1/3+1 = 53/84 = 0.63095...
(分数の横線は右端まで伸びていると思ってください)
ここで、実は、217 ≒ 312 は身近な所にあります。
完全5度12個 = 7オクターブ です! [(3/2)12 ≒ 27]
短三度4個 = 1オクターブ 、 長三度3個 = 1オクターブ はそれぞれ
(6/5)4=1296/625≒2 、 (5/4)3=125/64≒2
に現れています。美しいです。これが西洋音楽で、1オクターブを12に分けしめた元かもしれ
ません。(上より12以外の候補になるのは、7、17、41など素数ばかりで具合が悪そうです。)
7[211≒37]は、1オクターブを7つの白鍵に分けている所に使われていますね。別の表現
をすると、完全5度(1.5)を半音でみると、27/12 と捉えており、白鍵の個数(音階の元)で見る
と、24/7 と捉えている、ということになります。本当に驚きの気づきでした。
以下、工事中