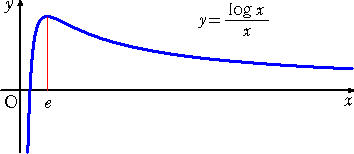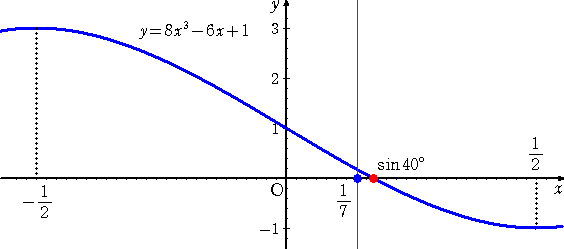微積分の小技　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

　このページでは、一見微積分とは無関係そうに見えるが、微積分を使うと鮮やかに解け
るというような問題を収集していこうと思う。

　平成１９年度入試で、次のような問題が出題された。

（問題その１）　　９９101 と　１０１99　の大小を比べよ。　　（東北学院大学　工学部）

（→　参考類題 ： 微分の効用）

　対数表が手元にあれば次のように解けるだろう。

　　１０１×log10９９＝１０１×（１＋０．９９５６）＝２０１．５５５６

　　９９×log10１０１＝９９×（２＋０．００４３）＝１９８．４２５７

よって、　１０１×log10９９＞９９×log10１０１　なので、　９９101＞１０１99　である。


　実際は、この問題の導入として微分の問題が出題されているので微分を使って解くのが
筋だろう。もっとも普段手元に対数表などない方が自然なので、微分を使うことに当然気が
つくはずである。


　上記の問題で、「１０１×log10９９＞９９×log10１０１」　から、

　　（log10９９）/９９＞（log10１０１）/１０１

であるが、微分を使うことを考えると、自然対数を用いて　（log９９）/９９＞（log１０１）/１０１

という形の方が自然だろう。

　このことから、　関数 Ｆ（ｘ）＝(log ｘ)/ｘ　の増減を調べることにより解決できる。

実際に、　Ｆ’（ｘ）＝（１−log ｘ）/ｘ2　、Ｆ”（ｘ）＝（２log ｘ−３）/ｘ3

　　ｘ →＋０　のとき、　Ｆ（ｘ）→−∞　　　、　ｘ →＋∞　のとき、　Ｆ（ｘ）→０

なので、下図を得る。

　

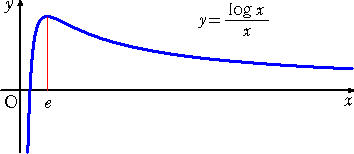
したがって、関数 Ｆ（ｘ） は、ｘ＞ｅ において単調に減少するので、

　（log９９）/９９＞（log１０１）/１０１　すなわち、　９９101＞１０１99　となる。


　この問題のように、何気ない問題にも微分は大きな力となる。微積分は入試問題におけ
る非常に強力な計算技術と言える。

（問題その２）
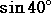　　　　　　　　　 　と 　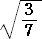 　の大小を比べよ。

　この問題は、平成１９年１０月１３日付けで、当ＨＰの掲示板「出会いの泉」に、当ＨＰが大
変お世話になっている Ａ’ｚ さんが紹介されたものである。高校２年生レベルの良問であろ
う。

（解）　　sin2４０°＝（１−cos８０°）/２＝（１−sin１０°）/２

　したがって、（１−sin１０°）/２ と ３/７ の大小を調べるには、sin１０°と １/７ の大小を調
べればよい。

　sin１０°＝θ　とおくと、　sin３０°＝１/２　より、　３sin１０°−４sin3１０°＝１/２

なので、　θ　は、３次方程式　８Ｘ3−６Ｘ＋１＝０　の解である。

　明らかに、　０＜θ＜１/２　である。

　いま、　Ｆ(Ｘ)＝８Ｘ3−６Ｘ＋１　とおくと、　Ｆ’(Ｘ)＝２４Ｘ2−６　で、　Ｆ’(Ｘ)＝０　とおくと、

Ｘ＝±１/２である。

　　

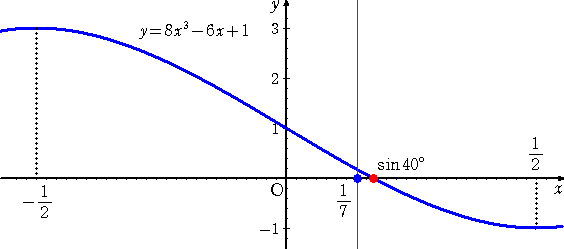
　したがって、　Ｙ＝Ｆ(Ｘ) は、 ０＜Ｘ＜１/２ の範囲で Ｘ 軸とただ１点で交わり、その区間で
単調に減少する。

　このとき、　　Ｆ(１/７)＝５７/３４３＞０　なので、　１/７ ＜ sin１０°

　よって、　sin2４０°＝（１−sin１０°）/２＜３/７　から、

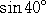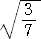　 　＜ 　 　　が成り立つ。　（終）


（コメント）　上記のグラフからも分かるように、２数の差は僅少ですね！正直に告白すると、
　　　　　当初、sin７．５°を使って計算しましたが、近似誤差が大きすぎて失敗しました！

　この問題も微分の恩恵を十分に受けている問題ですね！

　微分を使わないと途方に暮れてしまいそう．．．と思いきや、微分を使わずとも、 sin１０°
と １/７ の大小は調べられるということを、当ＨＰがいつもお世話になっているらすかるさん
から、ご教示いただいた。

（ sin１０°＞ １/７　であることの証明 ）

　sinθ ＝ １/７　とおく。ただし、　０°＜θ＜３０°とする。

このとき、　０°＜３θ＜９０°において、

　sin３θ ＝ ３sinθ−４sin3θ＝３/７−４/３４３＝１４３/３４３＜１/２

よって、　　０°＜３θ＜３０°　より、　０°＜θ＜１０°　なので、

　sinθ ＜ sin１０°　すなわち、　１/７ ＜ sin１０°

が成り立つ。


（コメント）　関数を微分したら綺麗に極値を与える ｘ の値が求められたので、グラフを利用
　　　　　する解法に誘惑されました。微分を使わず、簡潔で分かりやすくなりましたね！
　　　　　らすかるさんに感謝いたします。


　また、らすかるさんから、上記の問題を幾何的に示す方法がある旨、ご教示いただいた。

（証明）

　　　左図のようなひし形 ＡＢＣＤ において、
　　∠Ａ＝１２０°、ＡＢ＝２　とする。
　　　また、辺 ＣＤ 、 ＡＤ の中点をそれぞれ
　　Ｅ 、Ｆ とし、線分 ＢＥ 、ＢＦ と対角線 ＡＣ
　　との交点をそれぞれ Ｇ、Ｈ とする。

このとき、　ＣＦ＝　、ＢＦ＝　なので、

　　ｓｉｎ∠ＦＢＣ ＝

が成り立つ。（　←　なるほど！このような図形を考えると、右辺の奇妙な分数の出所が分
かるんですね．．．。）

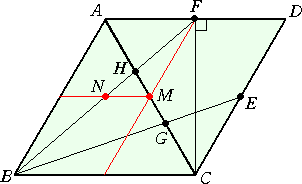
　ところで、∠ＦＢＣ＞４０°であることが、次の図とじっとにらめっこをすると分かる。

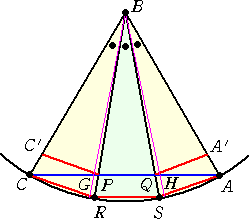　　正三角形 ABC において、点Ｂを中心として半径
　ＡＢ の円弧を描く。∠Ｂ の ３ 等分線と円弧との交
　点をそれぞれ Ｒ 、Ｓ とおき、線分 ＢＲ 、ＢＳ と線
　分 ＣＡ との交点をそれぞれ Ｐ 、Ｑ とする。

　　このとき、左図から分かるように、
　　　　 　　　ＣＰ ＝ ＡＱ ＞ ＰＱ
　である。

　したがって、線分 ＣＡ の３等分点をＧ 、Ｈとすると
　き、　∠ＨＢＣ＞４０°である。

　すなわち、上のひし形の図において、　∠ＦＢＣ＞４０°である。

したがって、
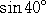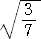　　　　　　　　　 　＜ 　 　　が成り立つ。　　（証終）


（コメント）　らすかるさんの証明をなぞってみましたが、私的には、

　ｓｉｎ∠ＦＢＣ 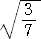＝ 　かつ、 　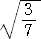 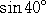＞ 　より、

　∠ＦＢＣ＞４０°

という論理の流れの方が自然に感じました。




　　　以下、工事中！